
Date: 2021-07-26 10:29:37 CEST, cola version: 1.9.4
Document is loading... 
First the variable is renamed to res_rh.
res_rh = rh
The partition hierarchy and all available functions which can be applied to res_rh object.
res_rh
#> A 'HierarchicalPartition' object with 'ATC:skmeans' method.
#> On a matrix with 12574 rows and 379 columns.
#> Performed in total 3150 partitions.
#> There are 13 groups under the following parameters:
#> - min_samples: 6
#> - mean_silhouette_cutoff: 0.9
#> - min_n_signatures: 252 (signatures are selected based on:)
#> - fdr_cutoff: 0.05
#> - group_diff (scaled values): 0.5
#>
#> Hierarchy of the partition:
#> 0, 379 cols
#> |-- 01, 93 cols, 703 signatures
#> | |-- 011, 49 cols (a)
#> | |-- 012, 31 cols, 0 signatures (c)
#> | `-- 013, 13 cols, 1 signatures (c)
#> |-- 02, 124 cols, 1267 signatures
#> | |-- 021, 76 cols, 305 signatures
#> | | |-- 0211, 31 cols, 90 signatures (c)
#> | | `-- 0212, 45 cols, 80 signatures (c)
#> | `-- 022, 48 cols, 844 signatures
#> | |-- 0221, 27 cols, 614 signatures
#> | | |-- 02211, 13 cols, 0 signatures (c)
#> | | |-- 02212, 11 cols (b)
#> | | `-- 02213, 3 cols (b)
#> | `-- 0222, 21 cols, 129 signatures (c)
#> |-- 03, 89 cols, 404 signatures
#> | |-- 031, 52 cols (a)
#> | `-- 032, 37 cols, 39 signatures (c)
#> `-- 04, 73 cols, 365 signatures
#> |-- 041, 51 cols (a)
#> `-- 042, 22 cols, 105 signatures (c)
#> Stop reason:
#> a) Mean silhouette score was too small
#> b) Subgroup had too few columns.
#> c) There were too few signatures.
#>
#> Following methods can be applied to this 'HierarchicalPartition' object:
#> [1] "all_leaves" "all_nodes" "cola_report" "collect_classes"
#> [5] "colnames" "compare_signatures" "dimension_reduction" "functional_enrichment"
#> [9] "get_anno_col" "get_anno" "get_children_nodes" "get_classes"
#> [13] "get_matrix" "get_signatures" "is_leaf_node" "max_depth"
#> [17] "merge_node" "ncol" "node_info" "node_level"
#> [21] "nrow" "rownames" "show" "split_node"
#> [25] "suggest_best_k" "test_to_known_factors" "top_rows_heatmap" "top_rows_overlap"
#>
#> You can get result for a single node by e.g. object["01"]
The call of hierarchical_partition() was:
#> hierarchical_partition(data = mat, anno = anno, subset = 500, cores = 4)
Dimension of the input matrix:
mat = get_matrix(res_rh)
dim(mat)
#> [1] 12574 379
All the methods that were tried:
res_rh@param$combination_method
#> [[1]]
#> [1] "ATC" "skmeans"
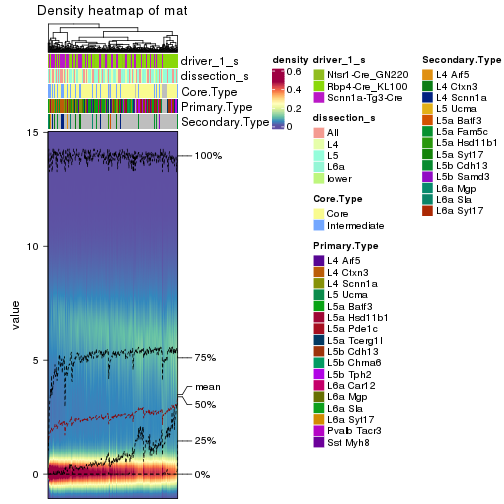
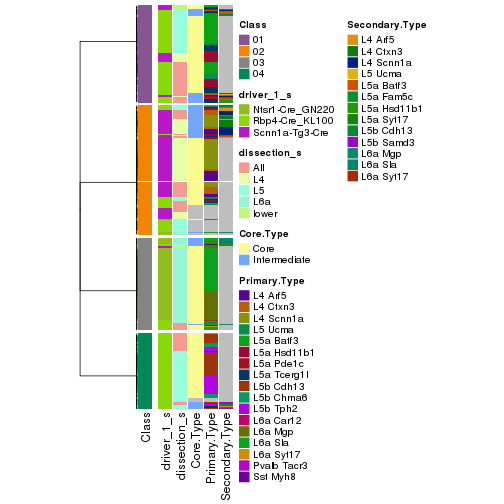
The density distribution for each sample is visualized as one column in the following heatmap. The clustering is based on the distance which is the Kolmogorov-Smirnov statistic between two distributions.
library(ComplexHeatmap)
densityHeatmap(mat, top_annotation = HeatmapAnnotation(df = get_anno(res_rh),
col = get_anno_col(res_rh)), ylab = "value", cluster_columns = TRUE, show_column_names = FALSE,
mc.cores = 1)
Some values about the hierarchy:
all_nodes(res_rh)
#> [1] "0" "01" "011" "012" "013" "02" "021" "0211" "0212" "022" "0221" "02211"
#> [13] "02212" "02213" "0222" "03" "031" "032" "04" "041" "042"
all_leaves(res_rh)
#> [1] "011" "012" "013" "0211" "0212" "02211" "02212" "02213" "0222" "031" "032" "041"
#> [13] "042"
node_info(res_rh)
#> id best_method depth best_k n_columns n_signatures p_signatures is_leaf
#> 1 0 ATC:skmeans 1 4 379 5059 4.02e-01 FALSE
#> 2 01 ATC:skmeans 2 3 93 703 5.59e-02 FALSE
#> 3 011 ATC:skmeans 3 2 49 NA NA TRUE
#> 4 012 ATC:skmeans 3 2 31 0 0.00e+00 TRUE
#> 5 013 ATC:skmeans 3 2 13 1 7.95e-05 TRUE
#> 6 02 ATC:skmeans 2 2 124 1267 1.01e-01 FALSE
#> 7 021 ATC:skmeans 3 2 76 305 2.43e-02 FALSE
#> 8 0211 ATC:skmeans 4 2 31 90 7.16e-03 TRUE
#> 9 0212 ATC:skmeans 4 2 45 80 6.36e-03 TRUE
#> 10 022 ATC:skmeans 3 2 48 844 6.71e-02 FALSE
#> 11 0221 ATC:skmeans 4 3 27 614 4.88e-02 FALSE
#> 12 02211 ATC:skmeans 5 2 13 0 0.00e+00 TRUE
#> 13 02212 not applied 5 NA 11 NA NA TRUE
#> 14 02213 not applied 5 NA 3 NA NA TRUE
#> 15 0222 ATC:skmeans 4 2 21 129 1.03e-02 TRUE
#> 16 03 ATC:skmeans 2 2 89 404 3.21e-02 FALSE
#> 17 031 ATC:skmeans 3 2 52 NA NA TRUE
#> 18 032 ATC:skmeans 3 2 37 39 3.10e-03 TRUE
#> 19 04 ATC:skmeans 2 2 73 365 2.90e-02 FALSE
#> 20 041 ATC:skmeans 3 4 51 NA NA TRUE
#> 21 042 ATC:skmeans 3 2 22 105 8.35e-03 TRUE
In the output from node_info(), there are the following columns:
id: The node id.best_method: The best method selected.depth: Depth of the node in the hierarchy.best_k: Best number of groups of the partition on that node.n_columns: Number of columns in the submatrix.n_signatures: Number of signatures with the best_k.p_signatures: Proportion of hte signatures in total number of rows in the matrix.is_leaf: Whether the node is a leaf.Labels of nodes are encoded in a special way. The number of digits correspond to the depth of the node in the hierarchy and the value of the digits correspond to the index of the subgroup in the current node, E.g. a label of “012” means the node is the second subgroup of the partition which is the first subgroup of the root node.
Following table shows the best k (number of partitions) for each node in the
partition hierarchy. Clicking on the node name in the table goes to the
corresponding section for the partitioning on that node.
The cola vignette explains the definition of the metrics used for determining the best number of partitions.
suggest_best_k(res_rh)
| Node | Best method | Is leaf | Best k | 1-PAC | Mean silhouette | Concordance | #samples | |
|---|---|---|---|---|---|---|---|---|
| Node0 | ATC:skmeans | 4 | 1.00 | 0.98 | 0.99 | 379 | ** | |
| Node01 | ATC:skmeans | 3 | 1.00 | 0.98 | 0.99 | 93 | ** | |
| Node011-leaf | ATC:skmeans | ✓ (a) | 2 | 0.87 | 0.88 | 0.95 | 49 | |
| Node012-leaf | ATC:skmeans | ✓ (c) | 2 | 0.80 | 0.93 | 0.97 | 31 | |
| Node013-leaf | ATC:skmeans | ✓ (c) | 2 | 1.00 | 0.99 | 0.99 | 13 | ** |
| Node02 | ATC:skmeans | 4 | 0.92 | 0.91 | 0.96 | 124 | * | |
| Node021 | ATC:skmeans | 3 | 0.92 | 0.92 | 0.96 | 76 | * | |
| Node0211-leaf | ATC:skmeans | ✓ (c) | 2 | 0.93 | 0.92 | 0.97 | 31 | * |
| Node0212-leaf | ATC:skmeans | ✓ (c) | 2 | 1.00 | 1.00 | 1.00 | 45 | ** |
| Node022 | ATC:skmeans | 2 | 1.00 | 0.99 | 1.00 | 48 | ** | |
| Node0221 | ATC:skmeans | 4 | 0.97 | 0.91 | 0.95 | 27 | ** | |
| Node02211-leaf | ATC:skmeans | ✓ (c) | 2 | 0.85 | 0.96 | 0.98 | 13 | |
| Node02212-leaf | not applied | ✓ (b) | 11 | |||||
| Node02213-leaf | not applied | ✓ (b) | 3 | |||||
| Node0222-leaf | ATC:skmeans | ✓ (c) | 2 | 1.00 | 1.00 | 1.00 | 21 | ** |
| Node03 | ATC:skmeans | 3 | 0.98 | 0.93 | 0.97 | 89 | ** | |
| Node031-leaf | ATC:skmeans | ✓ (a) | 2 | 0.76 | 0.88 | 0.95 | 52 | |
| Node032-leaf | ATC:skmeans | ✓ (c) | 2 | 1.00 | 0.95 | 0.98 | 37 | ** |
| Node04 | ATC:skmeans | 2 | 1.00 | 0.98 | 0.99 | 73 | ** | |
| Node041-leaf | ATC:skmeans | ✓ (a) | 4 | 0.71 | 0.85 | 0.91 | 51 | |
| Node042-leaf | ATC:skmeans | ✓ (c) | 3 | 0.95 | 0.81 | 0.93 | 22 | ** |
Stop reason: a) Mean silhouette score was too small b) Subgroup had too few columns. c) There were too few signatures.
**: 1-PAC > 0.95, *: 1-PAC > 0.9
The nodes of the hierarchy can be merged by setting the merge_node parameters. Here we
control the hierarchy with the min_n_signatures parameter. The value of min_n_signatures is
from node_info().
collect_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 305))
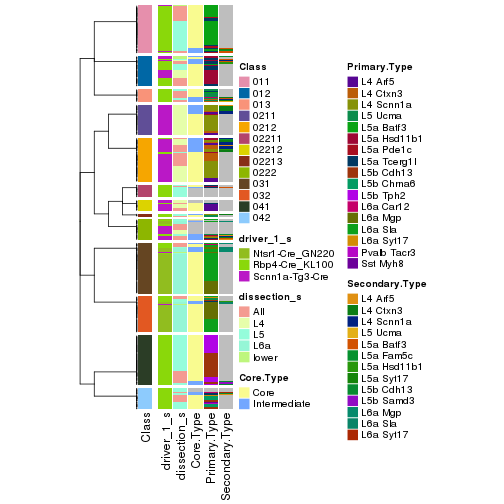
collect_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 365))
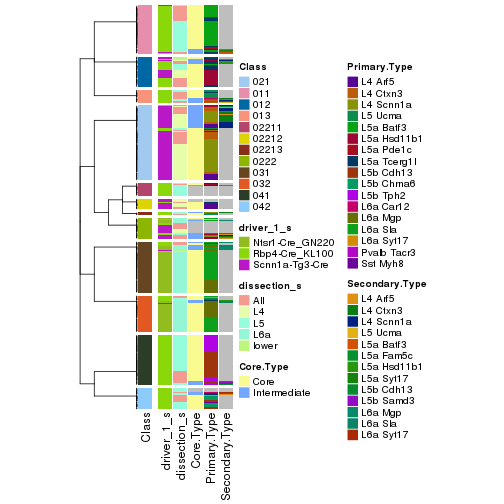
collect_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 404))
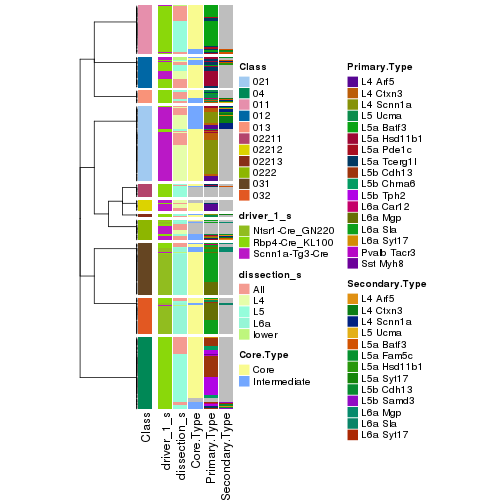
collect_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 614))
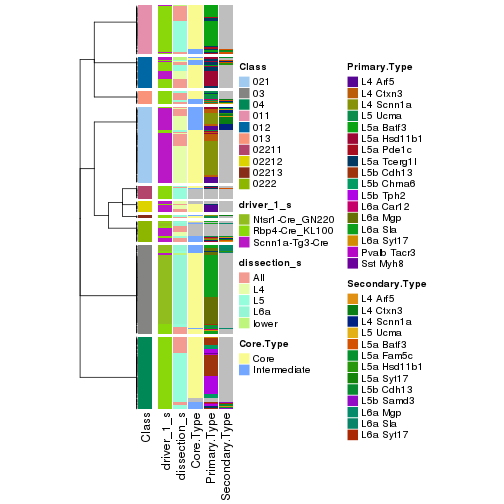
collect_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 703))
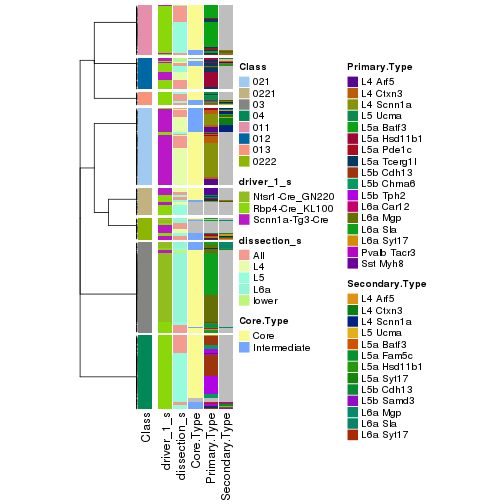
collect_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 844))
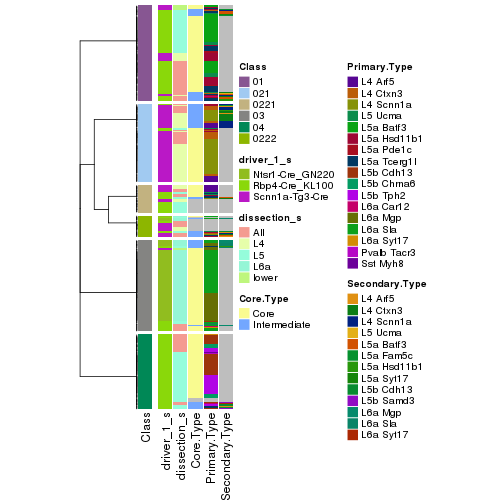
collect_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 1267))
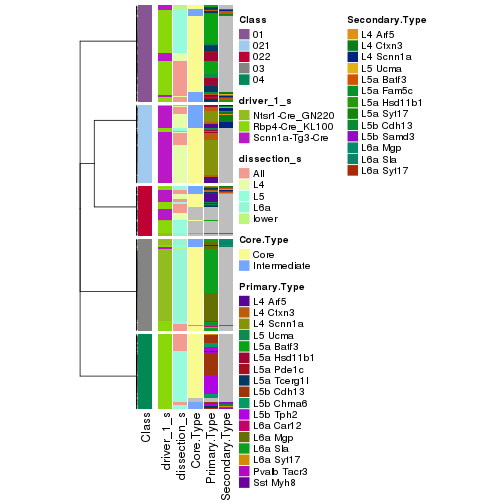
collect_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 5059))
Following shows the table of the partitions (You need to click the show/hide code output link to see it).
get_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 305))
#> SRR2140028 SRR2140022 SRR2140055 SRR2140083 SRR2139991 SRR2140067 SRR2140010 SRR2140031 SRR2140046
#> "0212" "0211" "0222" "02212" "0211" "0212" "0212" "0211" "0222"
#> SRR2140074 SRR2140003 SRR2139988 SRR2139982 SRR2140009 SRR2140004 SRR2140073 SRR2139985 SRR2140079
#> "0211" "0211" "02212" "0212" "0211" "012" "0211" "0212" "0222"
#> SRR2140041 SRR2140036 SRR2140084 SRR2139978 SRR2139996 SRR2140017 SRR2140060 SRR2140058 SRR2140052
#> "0222" "011" "02212" "0212" "0211" "0212" "0212" "0212" "0212"
#> SRR2140025 SRR2140056 SRR2140021 SRR2140013 SRR2140064 SRR2139998 SRR2139992 SRR2140019 SRR2140080
#> "0211" "0212" "0212" "0212" "0212" "0211" "0211" "0212" "0222"
#> SRR2140038 SRR2140045 SRR2140032 SRR2139981 SRR2140000 SRR2140077 SRR2139986 SRR2140070 SRR2140007
#> "032" "0212" "0211" "012" "0211" "0222" "0211" "0211" "0211"
#> SRR2140048 SRR2140035 SRR2140042 SRR2140063 SRR2140014 SRR2139995 SRR2140069 SRR2140026 SRR2140051
#> "0212" "012" "0212" "02212" "0211" "012" "012" "0212" "0212"
#> SRR2140061 SRR2140016 SRR2139979 SRR2139997 SRR2140085 SRR2140024 SRR2140053 SRR2140059 SRR2140078
#> "0212" "02212" "0212" "02212" "0222" "0211" "0212" "011" "0222"
#> SRR2139984 SRR2140072 SRR2140005 SRR2140037 SRR2140040 SRR2140047 SRR2140030 SRR2140008 SRR2139983
#> "0211" "012" "0211" "031" "012" "02212" "0212" "012" "0212"
#> SRR2139989 SRR2140002 SRR2140075 SRR2140054 SRR2140023 SRR2140029 SRR2140011 SRR2140066 SRR2139990
#> "0211" "0212" "0211" "0222" "0211" "0212" "0212" "0212" "0211"
#> SRR2140082 SRR2140086 SRR2140068 SRR2139994 SRR2140015 SRR2140062 SRR2140050 SRR2140027 SRR2140006
#> "02212" "0222" "0211" "0211" "012" "02212" "0212" "012" "0212"
#> SRR2140071 SRR2139987 SRR2140043 SRR2140034 SRR2140049 SRR2140033 SRR2140044 SRR2140039 SRR2140076
#> "012" "0211" "0212" "0211" "0212" "0212" "0212" "012" "0222"
#> SRR2140001 SRR2139980 SRR2140020 SRR2140057 SRR2140018 SRR2140081 SRR2139993 SRR2139999 SRR2139977
#> "0212" "0212" "0211" "0212" "02212" "0222" "0211" "0212" "0212"
#> SRR2140065 SRR2140012 SRR2139847 SRR2139830 SRR2139787 SRR2139769 SRR2139680 SRR2139714 SRR2139763
#> "0212" "0211" "0222" "011" "041" "041" "042" "042" "041"
#> SRR2139808 SRR2139802 SRR2139751 SRR2139726 SRR2139854 SRR2139823 SRR2139829 SRR2139693 SRR2139707
#> "041" "02211" "02213" "011" "02211" "013" "032" "011" "041"
#> SRR2139770 SRR2139699 SRR2139677 SRR2139794 SRR2139811 SRR2139742 SRR2139735 SRR2139748 SRR2139732
#> "02213" "042" "042" "042" "012" "041" "011" "041" "041"
#> SRR2139745 SRR2139738 SRR2139816 SRR2139799 SRR2139777 SRR2139700 SRR2139694 SRR2139793 SRR2139670
#> "041" "041" "041" "041" "041" "042" "011" "012" "011"
#> SRR2139824 SRR2139853 SRR2139721 SRR2139756 SRR2139805 SRR2139719 SRR2139780 SRR2139764 SRR2139713
#> "011" "02211" "0222" "011" "011" "042" "011" "011" "041"
#> SRR2139687 SRR2139669 SRR2139837 SRR2139840 SRR2139760 SRR2139683 SRR2139717 SRR2139784 SRR2139689
#> "012" "0212" "041" "013" "011" "041" "042" "011" "041"
#> SRR2139833 SRR2139844 SRR2139839 SRR2139725 SRR2139752 SRR2139758 SRR2139801 SRR2139779 SRR2139797
#> "042" "02211" "013" "041" "041" "041" "02211" "011" "011"
#> SRR2139674 SRR2139773 SRR2139690 SRR2139704 SRR2139820 SRR2139857 SRR2139736 SRR2139741 SRR2139818
#> "011" "011" "031" "02211" "041" "042" "041" "041" "011"
#> SRR2139812 SRR2139815 SRR2139746 SRR2139731 SRR2139850 SRR2139827 SRR2139673 SRR2139790 SRR2139709
#> "0212" "011" "0212" "011" "02211" "011" "011" "012" "011"
#> SRR2139679 SRR2139703 SRR2139697 SRR2139774 SRR2139806 SRR2139755 SRR2139722 SRR2139728 SRR2139843
#> "012" "012" "012" "042" "041" "041" "042" "041" "0222"
#> SRR2139834 SRR2139849 SRR2139710 SRR2139684 SRR2139767 SRR2139789 SRR2139783 SRR2139757 SRR2139720
#> "011" "02211" "042" "0212" "032" "032" "011" "032" "041"
#> SRR2139804 SRR2139712 SRR2139686 SRR2139765 SRR2139718 SRR2139781 SRR2139841 SRR2139836 SRR2139739
#> "012" "032" "012" "011" "011" "042" "011" "011" "011"
#> SRR2139744 SRR2139733 SRR2139817 SRR2139671 SRR2139792 SRR2139798 SRR2139701 SRR2139695 SRR2139776
#> "041" "011" "041" "013" "041" "041" "041" "042" "012"
#> SRR2139858 SRR2139852 SRR2139825 SRR2139828 SRR2139822 SRR2139855 SRR2139698 SRR2139795 SRR2139676
#> "042" "02211" "031" "031" "011" "02211" "02213" "041" "041"
#> SRR2139771 SRR2139692 SRR2139706 SRR2139810 SRR2139749 SRR2139734 SRR2139743 SRR2139831 SRR2139846
#> "013" "013" "042" "013" "041" "011" "041" "031" "02211"
#> SRR2139762 SRR2139681 SRR2139715 SRR2139786 SRR2139768 SRR2139803 SRR2139809 SRR2139727 SRR2139750
#> "011" "011" "013" "041" "041" "011" "011" "042" "041"
#> SRR2139807 SRR2139729 SRR2139723 SRR2139754 SRR2139848 SRR2139835 SRR2139842 SRR2139782 SRR2139766
#> "012" "0222" "011" "011" "042" "011" "0222" "041" "031"
#> SRR2139711 SRR2139685 SRR2139788 SRR2139814 SRR2139730 SRR2139747 SRR2139826 SRR2139851 SRR2139678
#> "041" "041" "042" "012" "013" "012" "012" "02211" "013"
#> SRR2139775 SRR2139702 SRR2139696 SRR2139791 SRR2139672 SRR2139708 SRR2139691 SRR2139705 SRR2139772
#> "041" "012" "012" "031" "011" "032" "013" "012" "011"
#> SRR2139778 SRR2139675 SRR2139796 SRR2139856 SRR2139821 SRR2139740 SRR2139737 SRR2139813 SRR2139819
#> "041" "042" "041" "042" "011" "041" "011" "02212" "041"
#> SRR2139785 SRR2139688 SRR2139682 SRR2139716 SRR2139761 SRR2139838 SRR2139845 SRR2139832 SRR2139759
#> "041" "013" "011" "041" "041" "013" "02211" "012" "041"
#> SRR2139753 SRR2139724 SRR2139800 SRR2139306 SRR2139371 SRR2139343 SRR2139334 SRR2139349 SRR2139368
#> "011" "011" "012" "031" "031" "032" "032" "032" "031"
#> SRR2139315 SRR2139362 SRR2139350 SRR2139327 SRR2139320 SRR2139357 SRR2139318 SRR2139381 SRR2139365
#> "031" "031" "032" "031" "031" "032" "031" "032" "032"
#> SRR2139312 SRR2139333 SRR2139344 SRR2139339 SRR2139376 SRR2139378 SRR2139372 SRR2139337 SRR2139340
#> "031" "0222" "032" "032" "031" "031" "032" "032" "032"
#> SRR2139361 SRR2139316 SRR2139324 SRR2139353 SRR2139359 SRR2139354 SRR2139323 SRR2139329 SRR2139311
#> "031" "031" "031" "032" "031" "032" "031" "031" "031"
#> SRR2139366 SRR2139382 SRR2139347 SRR2139330 SRR2139308 SRR2139375 SRR2139338 SRR2139345 SRR2139332
#> "031" "032" "032" "031" "031" "031" "032" "032" "032"
#> SRR2139377 SRR2139356 SRR2139321 SRR2139313 SRR2139364 SRR2139319 SRR2139380 SRR2139363 SRR2139314
#> "031" "031" "031" "031" "031" "032" "032" "031" "032"
#> SRR2139369 SRR2139326 SRR2139351 SRR2139370 SRR2139307 SRR2139348 SRR2139335 SRR2139342 SRR2139331
#> "031" "032" "031" "031" "031" "032" "032" "032" "031"
#> SRR2139346 SRR2139374 SRR2139309 SRR2139328 SRR2139322 SRR2139355 SRR2139383 SRR2139367 SRR2139310
#> "032" "031" "031" "031" "031" "032" "0222" "031" "031"
#> SRR2139384 SRR2139317 SRR2139360 SRR2139358 SRR2139352 SRR2139325 SRR2139373 SRR2139379 SRR2139341
#> "0222" "031" "031" "031" "031" "0222" "031" "031" "032"
#> SRR2139336
#> "032"
get_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 365))
#> SRR2140028 SRR2140022 SRR2140055 SRR2140083 SRR2139991 SRR2140067 SRR2140010 SRR2140031 SRR2140046
#> "021" "021" "0222" "02212" "021" "021" "021" "021" "0222"
#> SRR2140074 SRR2140003 SRR2139988 SRR2139982 SRR2140009 SRR2140004 SRR2140073 SRR2139985 SRR2140079
#> "021" "021" "02212" "021" "021" "012" "021" "021" "0222"
#> SRR2140041 SRR2140036 SRR2140084 SRR2139978 SRR2139996 SRR2140017 SRR2140060 SRR2140058 SRR2140052
#> "0222" "011" "02212" "021" "021" "021" "021" "021" "021"
#> SRR2140025 SRR2140056 SRR2140021 SRR2140013 SRR2140064 SRR2139998 SRR2139992 SRR2140019 SRR2140080
#> "021" "021" "021" "021" "021" "021" "021" "021" "0222"
#> SRR2140038 SRR2140045 SRR2140032 SRR2139981 SRR2140000 SRR2140077 SRR2139986 SRR2140070 SRR2140007
#> "032" "021" "021" "012" "021" "0222" "021" "021" "021"
#> SRR2140048 SRR2140035 SRR2140042 SRR2140063 SRR2140014 SRR2139995 SRR2140069 SRR2140026 SRR2140051
#> "021" "012" "021" "02212" "021" "012" "012" "021" "021"
#> SRR2140061 SRR2140016 SRR2139979 SRR2139997 SRR2140085 SRR2140024 SRR2140053 SRR2140059 SRR2140078
#> "021" "02212" "021" "02212" "0222" "021" "021" "011" "0222"
#> SRR2139984 SRR2140072 SRR2140005 SRR2140037 SRR2140040 SRR2140047 SRR2140030 SRR2140008 SRR2139983
#> "021" "012" "021" "031" "012" "02212" "021" "012" "021"
#> SRR2139989 SRR2140002 SRR2140075 SRR2140054 SRR2140023 SRR2140029 SRR2140011 SRR2140066 SRR2139990
#> "021" "021" "021" "0222" "021" "021" "021" "021" "021"
#> SRR2140082 SRR2140086 SRR2140068 SRR2139994 SRR2140015 SRR2140062 SRR2140050 SRR2140027 SRR2140006
#> "02212" "0222" "021" "021" "012" "02212" "021" "012" "021"
#> SRR2140071 SRR2139987 SRR2140043 SRR2140034 SRR2140049 SRR2140033 SRR2140044 SRR2140039 SRR2140076
#> "012" "021" "021" "021" "021" "021" "021" "012" "0222"
#> SRR2140001 SRR2139980 SRR2140020 SRR2140057 SRR2140018 SRR2140081 SRR2139993 SRR2139999 SRR2139977
#> "021" "021" "021" "021" "02212" "0222" "021" "021" "021"
#> SRR2140065 SRR2140012 SRR2139847 SRR2139830 SRR2139787 SRR2139769 SRR2139680 SRR2139714 SRR2139763
#> "021" "021" "0222" "011" "041" "041" "042" "042" "041"
#> SRR2139808 SRR2139802 SRR2139751 SRR2139726 SRR2139854 SRR2139823 SRR2139829 SRR2139693 SRR2139707
#> "041" "02211" "02213" "011" "02211" "013" "032" "011" "041"
#> SRR2139770 SRR2139699 SRR2139677 SRR2139794 SRR2139811 SRR2139742 SRR2139735 SRR2139748 SRR2139732
#> "02213" "042" "042" "042" "012" "041" "011" "041" "041"
#> SRR2139745 SRR2139738 SRR2139816 SRR2139799 SRR2139777 SRR2139700 SRR2139694 SRR2139793 SRR2139670
#> "041" "041" "041" "041" "041" "042" "011" "012" "011"
#> SRR2139824 SRR2139853 SRR2139721 SRR2139756 SRR2139805 SRR2139719 SRR2139780 SRR2139764 SRR2139713
#> "011" "02211" "0222" "011" "011" "042" "011" "011" "041"
#> SRR2139687 SRR2139669 SRR2139837 SRR2139840 SRR2139760 SRR2139683 SRR2139717 SRR2139784 SRR2139689
#> "012" "021" "041" "013" "011" "041" "042" "011" "041"
#> SRR2139833 SRR2139844 SRR2139839 SRR2139725 SRR2139752 SRR2139758 SRR2139801 SRR2139779 SRR2139797
#> "042" "02211" "013" "041" "041" "041" "02211" "011" "011"
#> SRR2139674 SRR2139773 SRR2139690 SRR2139704 SRR2139820 SRR2139857 SRR2139736 SRR2139741 SRR2139818
#> "011" "011" "031" "02211" "041" "042" "041" "041" "011"
#> SRR2139812 SRR2139815 SRR2139746 SRR2139731 SRR2139850 SRR2139827 SRR2139673 SRR2139790 SRR2139709
#> "021" "011" "021" "011" "02211" "011" "011" "012" "011"
#> SRR2139679 SRR2139703 SRR2139697 SRR2139774 SRR2139806 SRR2139755 SRR2139722 SRR2139728 SRR2139843
#> "012" "012" "012" "042" "041" "041" "042" "041" "0222"
#> SRR2139834 SRR2139849 SRR2139710 SRR2139684 SRR2139767 SRR2139789 SRR2139783 SRR2139757 SRR2139720
#> "011" "02211" "042" "021" "032" "032" "011" "032" "041"
#> SRR2139804 SRR2139712 SRR2139686 SRR2139765 SRR2139718 SRR2139781 SRR2139841 SRR2139836 SRR2139739
#> "012" "032" "012" "011" "011" "042" "011" "011" "011"
#> SRR2139744 SRR2139733 SRR2139817 SRR2139671 SRR2139792 SRR2139798 SRR2139701 SRR2139695 SRR2139776
#> "041" "011" "041" "013" "041" "041" "041" "042" "012"
#> SRR2139858 SRR2139852 SRR2139825 SRR2139828 SRR2139822 SRR2139855 SRR2139698 SRR2139795 SRR2139676
#> "042" "02211" "031" "031" "011" "02211" "02213" "041" "041"
#> SRR2139771 SRR2139692 SRR2139706 SRR2139810 SRR2139749 SRR2139734 SRR2139743 SRR2139831 SRR2139846
#> "013" "013" "042" "013" "041" "011" "041" "031" "02211"
#> SRR2139762 SRR2139681 SRR2139715 SRR2139786 SRR2139768 SRR2139803 SRR2139809 SRR2139727 SRR2139750
#> "011" "011" "013" "041" "041" "011" "011" "042" "041"
#> SRR2139807 SRR2139729 SRR2139723 SRR2139754 SRR2139848 SRR2139835 SRR2139842 SRR2139782 SRR2139766
#> "012" "0222" "011" "011" "042" "011" "0222" "041" "031"
#> SRR2139711 SRR2139685 SRR2139788 SRR2139814 SRR2139730 SRR2139747 SRR2139826 SRR2139851 SRR2139678
#> "041" "041" "042" "012" "013" "012" "012" "02211" "013"
#> SRR2139775 SRR2139702 SRR2139696 SRR2139791 SRR2139672 SRR2139708 SRR2139691 SRR2139705 SRR2139772
#> "041" "012" "012" "031" "011" "032" "013" "012" "011"
#> SRR2139778 SRR2139675 SRR2139796 SRR2139856 SRR2139821 SRR2139740 SRR2139737 SRR2139813 SRR2139819
#> "041" "042" "041" "042" "011" "041" "011" "02212" "041"
#> SRR2139785 SRR2139688 SRR2139682 SRR2139716 SRR2139761 SRR2139838 SRR2139845 SRR2139832 SRR2139759
#> "041" "013" "011" "041" "041" "013" "02211" "012" "041"
#> SRR2139753 SRR2139724 SRR2139800 SRR2139306 SRR2139371 SRR2139343 SRR2139334 SRR2139349 SRR2139368
#> "011" "011" "012" "031" "031" "032" "032" "032" "031"
#> SRR2139315 SRR2139362 SRR2139350 SRR2139327 SRR2139320 SRR2139357 SRR2139318 SRR2139381 SRR2139365
#> "031" "031" "032" "031" "031" "032" "031" "032" "032"
#> SRR2139312 SRR2139333 SRR2139344 SRR2139339 SRR2139376 SRR2139378 SRR2139372 SRR2139337 SRR2139340
#> "031" "0222" "032" "032" "031" "031" "032" "032" "032"
#> SRR2139361 SRR2139316 SRR2139324 SRR2139353 SRR2139359 SRR2139354 SRR2139323 SRR2139329 SRR2139311
#> "031" "031" "031" "032" "031" "032" "031" "031" "031"
#> SRR2139366 SRR2139382 SRR2139347 SRR2139330 SRR2139308 SRR2139375 SRR2139338 SRR2139345 SRR2139332
#> "031" "032" "032" "031" "031" "031" "032" "032" "032"
#> SRR2139377 SRR2139356 SRR2139321 SRR2139313 SRR2139364 SRR2139319 SRR2139380 SRR2139363 SRR2139314
#> "031" "031" "031" "031" "031" "032" "032" "031" "032"
#> SRR2139369 SRR2139326 SRR2139351 SRR2139370 SRR2139307 SRR2139348 SRR2139335 SRR2139342 SRR2139331
#> "031" "032" "031" "031" "031" "032" "032" "032" "031"
#> SRR2139346 SRR2139374 SRR2139309 SRR2139328 SRR2139322 SRR2139355 SRR2139383 SRR2139367 SRR2139310
#> "032" "031" "031" "031" "031" "032" "0222" "031" "031"
#> SRR2139384 SRR2139317 SRR2139360 SRR2139358 SRR2139352 SRR2139325 SRR2139373 SRR2139379 SRR2139341
#> "0222" "031" "031" "031" "031" "0222" "031" "031" "032"
#> SRR2139336
#> "032"
get_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 404))
#> SRR2140028 SRR2140022 SRR2140055 SRR2140083 SRR2139991 SRR2140067 SRR2140010 SRR2140031 SRR2140046
#> "021" "021" "0222" "02212" "021" "021" "021" "021" "0222"
#> SRR2140074 SRR2140003 SRR2139988 SRR2139982 SRR2140009 SRR2140004 SRR2140073 SRR2139985 SRR2140079
#> "021" "021" "02212" "021" "021" "012" "021" "021" "0222"
#> SRR2140041 SRR2140036 SRR2140084 SRR2139978 SRR2139996 SRR2140017 SRR2140060 SRR2140058 SRR2140052
#> "0222" "011" "02212" "021" "021" "021" "021" "021" "021"
#> SRR2140025 SRR2140056 SRR2140021 SRR2140013 SRR2140064 SRR2139998 SRR2139992 SRR2140019 SRR2140080
#> "021" "021" "021" "021" "021" "021" "021" "021" "0222"
#> SRR2140038 SRR2140045 SRR2140032 SRR2139981 SRR2140000 SRR2140077 SRR2139986 SRR2140070 SRR2140007
#> "032" "021" "021" "012" "021" "0222" "021" "021" "021"
#> SRR2140048 SRR2140035 SRR2140042 SRR2140063 SRR2140014 SRR2139995 SRR2140069 SRR2140026 SRR2140051
#> "021" "012" "021" "02212" "021" "012" "012" "021" "021"
#> SRR2140061 SRR2140016 SRR2139979 SRR2139997 SRR2140085 SRR2140024 SRR2140053 SRR2140059 SRR2140078
#> "021" "02212" "021" "02212" "0222" "021" "021" "011" "0222"
#> SRR2139984 SRR2140072 SRR2140005 SRR2140037 SRR2140040 SRR2140047 SRR2140030 SRR2140008 SRR2139983
#> "021" "012" "021" "031" "012" "02212" "021" "012" "021"
#> SRR2139989 SRR2140002 SRR2140075 SRR2140054 SRR2140023 SRR2140029 SRR2140011 SRR2140066 SRR2139990
#> "021" "021" "021" "0222" "021" "021" "021" "021" "021"
#> SRR2140082 SRR2140086 SRR2140068 SRR2139994 SRR2140015 SRR2140062 SRR2140050 SRR2140027 SRR2140006
#> "02212" "0222" "021" "021" "012" "02212" "021" "012" "021"
#> SRR2140071 SRR2139987 SRR2140043 SRR2140034 SRR2140049 SRR2140033 SRR2140044 SRR2140039 SRR2140076
#> "012" "021" "021" "021" "021" "021" "021" "012" "0222"
#> SRR2140001 SRR2139980 SRR2140020 SRR2140057 SRR2140018 SRR2140081 SRR2139993 SRR2139999 SRR2139977
#> "021" "021" "021" "021" "02212" "0222" "021" "021" "021"
#> SRR2140065 SRR2140012 SRR2139847 SRR2139830 SRR2139787 SRR2139769 SRR2139680 SRR2139714 SRR2139763
#> "021" "021" "0222" "011" "04" "04" "04" "04" "04"
#> SRR2139808 SRR2139802 SRR2139751 SRR2139726 SRR2139854 SRR2139823 SRR2139829 SRR2139693 SRR2139707
#> "04" "02211" "02213" "011" "02211" "013" "032" "011" "04"
#> SRR2139770 SRR2139699 SRR2139677 SRR2139794 SRR2139811 SRR2139742 SRR2139735 SRR2139748 SRR2139732
#> "02213" "04" "04" "04" "012" "04" "011" "04" "04"
#> SRR2139745 SRR2139738 SRR2139816 SRR2139799 SRR2139777 SRR2139700 SRR2139694 SRR2139793 SRR2139670
#> "04" "04" "04" "04" "04" "04" "011" "012" "011"
#> SRR2139824 SRR2139853 SRR2139721 SRR2139756 SRR2139805 SRR2139719 SRR2139780 SRR2139764 SRR2139713
#> "011" "02211" "0222" "011" "011" "04" "011" "011" "04"
#> SRR2139687 SRR2139669 SRR2139837 SRR2139840 SRR2139760 SRR2139683 SRR2139717 SRR2139784 SRR2139689
#> "012" "021" "04" "013" "011" "04" "04" "011" "04"
#> SRR2139833 SRR2139844 SRR2139839 SRR2139725 SRR2139752 SRR2139758 SRR2139801 SRR2139779 SRR2139797
#> "04" "02211" "013" "04" "04" "04" "02211" "011" "011"
#> SRR2139674 SRR2139773 SRR2139690 SRR2139704 SRR2139820 SRR2139857 SRR2139736 SRR2139741 SRR2139818
#> "011" "011" "031" "02211" "04" "04" "04" "04" "011"
#> SRR2139812 SRR2139815 SRR2139746 SRR2139731 SRR2139850 SRR2139827 SRR2139673 SRR2139790 SRR2139709
#> "021" "011" "021" "011" "02211" "011" "011" "012" "011"
#> SRR2139679 SRR2139703 SRR2139697 SRR2139774 SRR2139806 SRR2139755 SRR2139722 SRR2139728 SRR2139843
#> "012" "012" "012" "04" "04" "04" "04" "04" "0222"
#> SRR2139834 SRR2139849 SRR2139710 SRR2139684 SRR2139767 SRR2139789 SRR2139783 SRR2139757 SRR2139720
#> "011" "02211" "04" "021" "032" "032" "011" "032" "04"
#> SRR2139804 SRR2139712 SRR2139686 SRR2139765 SRR2139718 SRR2139781 SRR2139841 SRR2139836 SRR2139739
#> "012" "032" "012" "011" "011" "04" "011" "011" "011"
#> SRR2139744 SRR2139733 SRR2139817 SRR2139671 SRR2139792 SRR2139798 SRR2139701 SRR2139695 SRR2139776
#> "04" "011" "04" "013" "04" "04" "04" "04" "012"
#> SRR2139858 SRR2139852 SRR2139825 SRR2139828 SRR2139822 SRR2139855 SRR2139698 SRR2139795 SRR2139676
#> "04" "02211" "031" "031" "011" "02211" "02213" "04" "04"
#> SRR2139771 SRR2139692 SRR2139706 SRR2139810 SRR2139749 SRR2139734 SRR2139743 SRR2139831 SRR2139846
#> "013" "013" "04" "013" "04" "011" "04" "031" "02211"
#> SRR2139762 SRR2139681 SRR2139715 SRR2139786 SRR2139768 SRR2139803 SRR2139809 SRR2139727 SRR2139750
#> "011" "011" "013" "04" "04" "011" "011" "04" "04"
#> SRR2139807 SRR2139729 SRR2139723 SRR2139754 SRR2139848 SRR2139835 SRR2139842 SRR2139782 SRR2139766
#> "012" "0222" "011" "011" "04" "011" "0222" "04" "031"
#> SRR2139711 SRR2139685 SRR2139788 SRR2139814 SRR2139730 SRR2139747 SRR2139826 SRR2139851 SRR2139678
#> "04" "04" "04" "012" "013" "012" "012" "02211" "013"
#> SRR2139775 SRR2139702 SRR2139696 SRR2139791 SRR2139672 SRR2139708 SRR2139691 SRR2139705 SRR2139772
#> "04" "012" "012" "031" "011" "032" "013" "012" "011"
#> SRR2139778 SRR2139675 SRR2139796 SRR2139856 SRR2139821 SRR2139740 SRR2139737 SRR2139813 SRR2139819
#> "04" "04" "04" "04" "011" "04" "011" "02212" "04"
#> SRR2139785 SRR2139688 SRR2139682 SRR2139716 SRR2139761 SRR2139838 SRR2139845 SRR2139832 SRR2139759
#> "04" "013" "011" "04" "04" "013" "02211" "012" "04"
#> SRR2139753 SRR2139724 SRR2139800 SRR2139306 SRR2139371 SRR2139343 SRR2139334 SRR2139349 SRR2139368
#> "011" "011" "012" "031" "031" "032" "032" "032" "031"
#> SRR2139315 SRR2139362 SRR2139350 SRR2139327 SRR2139320 SRR2139357 SRR2139318 SRR2139381 SRR2139365
#> "031" "031" "032" "031" "031" "032" "031" "032" "032"
#> SRR2139312 SRR2139333 SRR2139344 SRR2139339 SRR2139376 SRR2139378 SRR2139372 SRR2139337 SRR2139340
#> "031" "0222" "032" "032" "031" "031" "032" "032" "032"
#> SRR2139361 SRR2139316 SRR2139324 SRR2139353 SRR2139359 SRR2139354 SRR2139323 SRR2139329 SRR2139311
#> "031" "031" "031" "032" "031" "032" "031" "031" "031"
#> SRR2139366 SRR2139382 SRR2139347 SRR2139330 SRR2139308 SRR2139375 SRR2139338 SRR2139345 SRR2139332
#> "031" "032" "032" "031" "031" "031" "032" "032" "032"
#> SRR2139377 SRR2139356 SRR2139321 SRR2139313 SRR2139364 SRR2139319 SRR2139380 SRR2139363 SRR2139314
#> "031" "031" "031" "031" "031" "032" "032" "031" "032"
#> SRR2139369 SRR2139326 SRR2139351 SRR2139370 SRR2139307 SRR2139348 SRR2139335 SRR2139342 SRR2139331
#> "031" "032" "031" "031" "031" "032" "032" "032" "031"
#> SRR2139346 SRR2139374 SRR2139309 SRR2139328 SRR2139322 SRR2139355 SRR2139383 SRR2139367 SRR2139310
#> "032" "031" "031" "031" "031" "032" "0222" "031" "031"
#> SRR2139384 SRR2139317 SRR2139360 SRR2139358 SRR2139352 SRR2139325 SRR2139373 SRR2139379 SRR2139341
#> "0222" "031" "031" "031" "031" "0222" "031" "031" "032"
#> SRR2139336
#> "032"
get_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 614))
#> SRR2140028 SRR2140022 SRR2140055 SRR2140083 SRR2139991 SRR2140067 SRR2140010 SRR2140031 SRR2140046
#> "021" "021" "0222" "02212" "021" "021" "021" "021" "0222"
#> SRR2140074 SRR2140003 SRR2139988 SRR2139982 SRR2140009 SRR2140004 SRR2140073 SRR2139985 SRR2140079
#> "021" "021" "02212" "021" "021" "012" "021" "021" "0222"
#> SRR2140041 SRR2140036 SRR2140084 SRR2139978 SRR2139996 SRR2140017 SRR2140060 SRR2140058 SRR2140052
#> "0222" "011" "02212" "021" "021" "021" "021" "021" "021"
#> SRR2140025 SRR2140056 SRR2140021 SRR2140013 SRR2140064 SRR2139998 SRR2139992 SRR2140019 SRR2140080
#> "021" "021" "021" "021" "021" "021" "021" "021" "0222"
#> SRR2140038 SRR2140045 SRR2140032 SRR2139981 SRR2140000 SRR2140077 SRR2139986 SRR2140070 SRR2140007
#> "03" "021" "021" "012" "021" "0222" "021" "021" "021"
#> SRR2140048 SRR2140035 SRR2140042 SRR2140063 SRR2140014 SRR2139995 SRR2140069 SRR2140026 SRR2140051
#> "021" "012" "021" "02212" "021" "012" "012" "021" "021"
#> SRR2140061 SRR2140016 SRR2139979 SRR2139997 SRR2140085 SRR2140024 SRR2140053 SRR2140059 SRR2140078
#> "021" "02212" "021" "02212" "0222" "021" "021" "011" "0222"
#> SRR2139984 SRR2140072 SRR2140005 SRR2140037 SRR2140040 SRR2140047 SRR2140030 SRR2140008 SRR2139983
#> "021" "012" "021" "03" "012" "02212" "021" "012" "021"
#> SRR2139989 SRR2140002 SRR2140075 SRR2140054 SRR2140023 SRR2140029 SRR2140011 SRR2140066 SRR2139990
#> "021" "021" "021" "0222" "021" "021" "021" "021" "021"
#> SRR2140082 SRR2140086 SRR2140068 SRR2139994 SRR2140015 SRR2140062 SRR2140050 SRR2140027 SRR2140006
#> "02212" "0222" "021" "021" "012" "02212" "021" "012" "021"
#> SRR2140071 SRR2139987 SRR2140043 SRR2140034 SRR2140049 SRR2140033 SRR2140044 SRR2140039 SRR2140076
#> "012" "021" "021" "021" "021" "021" "021" "012" "0222"
#> SRR2140001 SRR2139980 SRR2140020 SRR2140057 SRR2140018 SRR2140081 SRR2139993 SRR2139999 SRR2139977
#> "021" "021" "021" "021" "02212" "0222" "021" "021" "021"
#> SRR2140065 SRR2140012 SRR2139847 SRR2139830 SRR2139787 SRR2139769 SRR2139680 SRR2139714 SRR2139763
#> "021" "021" "0222" "011" "04" "04" "04" "04" "04"
#> SRR2139808 SRR2139802 SRR2139751 SRR2139726 SRR2139854 SRR2139823 SRR2139829 SRR2139693 SRR2139707
#> "04" "02211" "02213" "011" "02211" "013" "03" "011" "04"
#> SRR2139770 SRR2139699 SRR2139677 SRR2139794 SRR2139811 SRR2139742 SRR2139735 SRR2139748 SRR2139732
#> "02213" "04" "04" "04" "012" "04" "011" "04" "04"
#> SRR2139745 SRR2139738 SRR2139816 SRR2139799 SRR2139777 SRR2139700 SRR2139694 SRR2139793 SRR2139670
#> "04" "04" "04" "04" "04" "04" "011" "012" "011"
#> SRR2139824 SRR2139853 SRR2139721 SRR2139756 SRR2139805 SRR2139719 SRR2139780 SRR2139764 SRR2139713
#> "011" "02211" "0222" "011" "011" "04" "011" "011" "04"
#> SRR2139687 SRR2139669 SRR2139837 SRR2139840 SRR2139760 SRR2139683 SRR2139717 SRR2139784 SRR2139689
#> "012" "021" "04" "013" "011" "04" "04" "011" "04"
#> SRR2139833 SRR2139844 SRR2139839 SRR2139725 SRR2139752 SRR2139758 SRR2139801 SRR2139779 SRR2139797
#> "04" "02211" "013" "04" "04" "04" "02211" "011" "011"
#> SRR2139674 SRR2139773 SRR2139690 SRR2139704 SRR2139820 SRR2139857 SRR2139736 SRR2139741 SRR2139818
#> "011" "011" "03" "02211" "04" "04" "04" "04" "011"
#> SRR2139812 SRR2139815 SRR2139746 SRR2139731 SRR2139850 SRR2139827 SRR2139673 SRR2139790 SRR2139709
#> "021" "011" "021" "011" "02211" "011" "011" "012" "011"
#> SRR2139679 SRR2139703 SRR2139697 SRR2139774 SRR2139806 SRR2139755 SRR2139722 SRR2139728 SRR2139843
#> "012" "012" "012" "04" "04" "04" "04" "04" "0222"
#> SRR2139834 SRR2139849 SRR2139710 SRR2139684 SRR2139767 SRR2139789 SRR2139783 SRR2139757 SRR2139720
#> "011" "02211" "04" "021" "03" "03" "011" "03" "04"
#> SRR2139804 SRR2139712 SRR2139686 SRR2139765 SRR2139718 SRR2139781 SRR2139841 SRR2139836 SRR2139739
#> "012" "03" "012" "011" "011" "04" "011" "011" "011"
#> SRR2139744 SRR2139733 SRR2139817 SRR2139671 SRR2139792 SRR2139798 SRR2139701 SRR2139695 SRR2139776
#> "04" "011" "04" "013" "04" "04" "04" "04" "012"
#> SRR2139858 SRR2139852 SRR2139825 SRR2139828 SRR2139822 SRR2139855 SRR2139698 SRR2139795 SRR2139676
#> "04" "02211" "03" "03" "011" "02211" "02213" "04" "04"
#> SRR2139771 SRR2139692 SRR2139706 SRR2139810 SRR2139749 SRR2139734 SRR2139743 SRR2139831 SRR2139846
#> "013" "013" "04" "013" "04" "011" "04" "03" "02211"
#> SRR2139762 SRR2139681 SRR2139715 SRR2139786 SRR2139768 SRR2139803 SRR2139809 SRR2139727 SRR2139750
#> "011" "011" "013" "04" "04" "011" "011" "04" "04"
#> SRR2139807 SRR2139729 SRR2139723 SRR2139754 SRR2139848 SRR2139835 SRR2139842 SRR2139782 SRR2139766
#> "012" "0222" "011" "011" "04" "011" "0222" "04" "03"
#> SRR2139711 SRR2139685 SRR2139788 SRR2139814 SRR2139730 SRR2139747 SRR2139826 SRR2139851 SRR2139678
#> "04" "04" "04" "012" "013" "012" "012" "02211" "013"
#> SRR2139775 SRR2139702 SRR2139696 SRR2139791 SRR2139672 SRR2139708 SRR2139691 SRR2139705 SRR2139772
#> "04" "012" "012" "03" "011" "03" "013" "012" "011"
#> SRR2139778 SRR2139675 SRR2139796 SRR2139856 SRR2139821 SRR2139740 SRR2139737 SRR2139813 SRR2139819
#> "04" "04" "04" "04" "011" "04" "011" "02212" "04"
#> SRR2139785 SRR2139688 SRR2139682 SRR2139716 SRR2139761 SRR2139838 SRR2139845 SRR2139832 SRR2139759
#> "04" "013" "011" "04" "04" "013" "02211" "012" "04"
#> SRR2139753 SRR2139724 SRR2139800 SRR2139306 SRR2139371 SRR2139343 SRR2139334 SRR2139349 SRR2139368
#> "011" "011" "012" "03" "03" "03" "03" "03" "03"
#> SRR2139315 SRR2139362 SRR2139350 SRR2139327 SRR2139320 SRR2139357 SRR2139318 SRR2139381 SRR2139365
#> "03" "03" "03" "03" "03" "03" "03" "03" "03"
#> SRR2139312 SRR2139333 SRR2139344 SRR2139339 SRR2139376 SRR2139378 SRR2139372 SRR2139337 SRR2139340
#> "03" "0222" "03" "03" "03" "03" "03" "03" "03"
#> SRR2139361 SRR2139316 SRR2139324 SRR2139353 SRR2139359 SRR2139354 SRR2139323 SRR2139329 SRR2139311
#> "03" "03" "03" "03" "03" "03" "03" "03" "03"
#> SRR2139366 SRR2139382 SRR2139347 SRR2139330 SRR2139308 SRR2139375 SRR2139338 SRR2139345 SRR2139332
#> "03" "03" "03" "03" "03" "03" "03" "03" "03"
#> SRR2139377 SRR2139356 SRR2139321 SRR2139313 SRR2139364 SRR2139319 SRR2139380 SRR2139363 SRR2139314
#> "03" "03" "03" "03" "03" "03" "03" "03" "03"
#> SRR2139369 SRR2139326 SRR2139351 SRR2139370 SRR2139307 SRR2139348 SRR2139335 SRR2139342 SRR2139331
#> "03" "03" "03" "03" "03" "03" "03" "03" "03"
#> SRR2139346 SRR2139374 SRR2139309 SRR2139328 SRR2139322 SRR2139355 SRR2139383 SRR2139367 SRR2139310
#> "03" "03" "03" "03" "03" "03" "0222" "03" "03"
#> SRR2139384 SRR2139317 SRR2139360 SRR2139358 SRR2139352 SRR2139325 SRR2139373 SRR2139379 SRR2139341
#> "0222" "03" "03" "03" "03" "0222" "03" "03" "03"
#> SRR2139336
#> "03"
get_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 703))
#> SRR2140028 SRR2140022 SRR2140055 SRR2140083 SRR2139991 SRR2140067 SRR2140010 SRR2140031 SRR2140046
#> "021" "021" "0222" "0221" "021" "021" "021" "021" "0222"
#> SRR2140074 SRR2140003 SRR2139988 SRR2139982 SRR2140009 SRR2140004 SRR2140073 SRR2139985 SRR2140079
#> "021" "021" "0221" "021" "021" "012" "021" "021" "0222"
#> SRR2140041 SRR2140036 SRR2140084 SRR2139978 SRR2139996 SRR2140017 SRR2140060 SRR2140058 SRR2140052
#> "0222" "011" "0221" "021" "021" "021" "021" "021" "021"
#> SRR2140025 SRR2140056 SRR2140021 SRR2140013 SRR2140064 SRR2139998 SRR2139992 SRR2140019 SRR2140080
#> "021" "021" "021" "021" "021" "021" "021" "021" "0222"
#> SRR2140038 SRR2140045 SRR2140032 SRR2139981 SRR2140000 SRR2140077 SRR2139986 SRR2140070 SRR2140007
#> "03" "021" "021" "012" "021" "0222" "021" "021" "021"
#> SRR2140048 SRR2140035 SRR2140042 SRR2140063 SRR2140014 SRR2139995 SRR2140069 SRR2140026 SRR2140051
#> "021" "012" "021" "0221" "021" "012" "012" "021" "021"
#> SRR2140061 SRR2140016 SRR2139979 SRR2139997 SRR2140085 SRR2140024 SRR2140053 SRR2140059 SRR2140078
#> "021" "0221" "021" "0221" "0222" "021" "021" "011" "0222"
#> SRR2139984 SRR2140072 SRR2140005 SRR2140037 SRR2140040 SRR2140047 SRR2140030 SRR2140008 SRR2139983
#> "021" "012" "021" "03" "012" "0221" "021" "012" "021"
#> SRR2139989 SRR2140002 SRR2140075 SRR2140054 SRR2140023 SRR2140029 SRR2140011 SRR2140066 SRR2139990
#> "021" "021" "021" "0222" "021" "021" "021" "021" "021"
#> SRR2140082 SRR2140086 SRR2140068 SRR2139994 SRR2140015 SRR2140062 SRR2140050 SRR2140027 SRR2140006
#> "0221" "0222" "021" "021" "012" "0221" "021" "012" "021"
#> SRR2140071 SRR2139987 SRR2140043 SRR2140034 SRR2140049 SRR2140033 SRR2140044 SRR2140039 SRR2140076
#> "012" "021" "021" "021" "021" "021" "021" "012" "0222"
#> SRR2140001 SRR2139980 SRR2140020 SRR2140057 SRR2140018 SRR2140081 SRR2139993 SRR2139999 SRR2139977
#> "021" "021" "021" "021" "0221" "0222" "021" "021" "021"
#> SRR2140065 SRR2140012 SRR2139847 SRR2139830 SRR2139787 SRR2139769 SRR2139680 SRR2139714 SRR2139763
#> "021" "021" "0222" "011" "04" "04" "04" "04" "04"
#> SRR2139808 SRR2139802 SRR2139751 SRR2139726 SRR2139854 SRR2139823 SRR2139829 SRR2139693 SRR2139707
#> "04" "0221" "0221" "011" "0221" "013" "03" "011" "04"
#> SRR2139770 SRR2139699 SRR2139677 SRR2139794 SRR2139811 SRR2139742 SRR2139735 SRR2139748 SRR2139732
#> "0221" "04" "04" "04" "012" "04" "011" "04" "04"
#> SRR2139745 SRR2139738 SRR2139816 SRR2139799 SRR2139777 SRR2139700 SRR2139694 SRR2139793 SRR2139670
#> "04" "04" "04" "04" "04" "04" "011" "012" "011"
#> SRR2139824 SRR2139853 SRR2139721 SRR2139756 SRR2139805 SRR2139719 SRR2139780 SRR2139764 SRR2139713
#> "011" "0221" "0222" "011" "011" "04" "011" "011" "04"
#> SRR2139687 SRR2139669 SRR2139837 SRR2139840 SRR2139760 SRR2139683 SRR2139717 SRR2139784 SRR2139689
#> "012" "021" "04" "013" "011" "04" "04" "011" "04"
#> SRR2139833 SRR2139844 SRR2139839 SRR2139725 SRR2139752 SRR2139758 SRR2139801 SRR2139779 SRR2139797
#> "04" "0221" "013" "04" "04" "04" "0221" "011" "011"
#> SRR2139674 SRR2139773 SRR2139690 SRR2139704 SRR2139820 SRR2139857 SRR2139736 SRR2139741 SRR2139818
#> "011" "011" "03" "0221" "04" "04" "04" "04" "011"
#> SRR2139812 SRR2139815 SRR2139746 SRR2139731 SRR2139850 SRR2139827 SRR2139673 SRR2139790 SRR2139709
#> "021" "011" "021" "011" "0221" "011" "011" "012" "011"
#> SRR2139679 SRR2139703 SRR2139697 SRR2139774 SRR2139806 SRR2139755 SRR2139722 SRR2139728 SRR2139843
#> "012" "012" "012" "04" "04" "04" "04" "04" "0222"
#> SRR2139834 SRR2139849 SRR2139710 SRR2139684 SRR2139767 SRR2139789 SRR2139783 SRR2139757 SRR2139720
#> "011" "0221" "04" "021" "03" "03" "011" "03" "04"
#> SRR2139804 SRR2139712 SRR2139686 SRR2139765 SRR2139718 SRR2139781 SRR2139841 SRR2139836 SRR2139739
#> "012" "03" "012" "011" "011" "04" "011" "011" "011"
#> SRR2139744 SRR2139733 SRR2139817 SRR2139671 SRR2139792 SRR2139798 SRR2139701 SRR2139695 SRR2139776
#> "04" "011" "04" "013" "04" "04" "04" "04" "012"
#> SRR2139858 SRR2139852 SRR2139825 SRR2139828 SRR2139822 SRR2139855 SRR2139698 SRR2139795 SRR2139676
#> "04" "0221" "03" "03" "011" "0221" "0221" "04" "04"
#> SRR2139771 SRR2139692 SRR2139706 SRR2139810 SRR2139749 SRR2139734 SRR2139743 SRR2139831 SRR2139846
#> "013" "013" "04" "013" "04" "011" "04" "03" "0221"
#> SRR2139762 SRR2139681 SRR2139715 SRR2139786 SRR2139768 SRR2139803 SRR2139809 SRR2139727 SRR2139750
#> "011" "011" "013" "04" "04" "011" "011" "04" "04"
#> SRR2139807 SRR2139729 SRR2139723 SRR2139754 SRR2139848 SRR2139835 SRR2139842 SRR2139782 SRR2139766
#> "012" "0222" "011" "011" "04" "011" "0222" "04" "03"
#> SRR2139711 SRR2139685 SRR2139788 SRR2139814 SRR2139730 SRR2139747 SRR2139826 SRR2139851 SRR2139678
#> "04" "04" "04" "012" "013" "012" "012" "0221" "013"
#> SRR2139775 SRR2139702 SRR2139696 SRR2139791 SRR2139672 SRR2139708 SRR2139691 SRR2139705 SRR2139772
#> "04" "012" "012" "03" "011" "03" "013" "012" "011"
#> SRR2139778 SRR2139675 SRR2139796 SRR2139856 SRR2139821 SRR2139740 SRR2139737 SRR2139813 SRR2139819
#> "04" "04" "04" "04" "011" "04" "011" "0221" "04"
#> SRR2139785 SRR2139688 SRR2139682 SRR2139716 SRR2139761 SRR2139838 SRR2139845 SRR2139832 SRR2139759
#> "04" "013" "011" "04" "04" "013" "0221" "012" "04"
#> SRR2139753 SRR2139724 SRR2139800 SRR2139306 SRR2139371 SRR2139343 SRR2139334 SRR2139349 SRR2139368
#> "011" "011" "012" "03" "03" "03" "03" "03" "03"
#> SRR2139315 SRR2139362 SRR2139350 SRR2139327 SRR2139320 SRR2139357 SRR2139318 SRR2139381 SRR2139365
#> "03" "03" "03" "03" "03" "03" "03" "03" "03"
#> SRR2139312 SRR2139333 SRR2139344 SRR2139339 SRR2139376 SRR2139378 SRR2139372 SRR2139337 SRR2139340
#> "03" "0222" "03" "03" "03" "03" "03" "03" "03"
#> SRR2139361 SRR2139316 SRR2139324 SRR2139353 SRR2139359 SRR2139354 SRR2139323 SRR2139329 SRR2139311
#> "03" "03" "03" "03" "03" "03" "03" "03" "03"
#> SRR2139366 SRR2139382 SRR2139347 SRR2139330 SRR2139308 SRR2139375 SRR2139338 SRR2139345 SRR2139332
#> "03" "03" "03" "03" "03" "03" "03" "03" "03"
#> SRR2139377 SRR2139356 SRR2139321 SRR2139313 SRR2139364 SRR2139319 SRR2139380 SRR2139363 SRR2139314
#> "03" "03" "03" "03" "03" "03" "03" "03" "03"
#> SRR2139369 SRR2139326 SRR2139351 SRR2139370 SRR2139307 SRR2139348 SRR2139335 SRR2139342 SRR2139331
#> "03" "03" "03" "03" "03" "03" "03" "03" "03"
#> SRR2139346 SRR2139374 SRR2139309 SRR2139328 SRR2139322 SRR2139355 SRR2139383 SRR2139367 SRR2139310
#> "03" "03" "03" "03" "03" "03" "0222" "03" "03"
#> SRR2139384 SRR2139317 SRR2139360 SRR2139358 SRR2139352 SRR2139325 SRR2139373 SRR2139379 SRR2139341
#> "0222" "03" "03" "03" "03" "0222" "03" "03" "03"
#> SRR2139336
#> "03"
get_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 844))
#> SRR2140028 SRR2140022 SRR2140055 SRR2140083 SRR2139991 SRR2140067 SRR2140010 SRR2140031 SRR2140046
#> "021" "021" "0222" "0221" "021" "021" "021" "021" "0222"
#> SRR2140074 SRR2140003 SRR2139988 SRR2139982 SRR2140009 SRR2140004 SRR2140073 SRR2139985 SRR2140079
#> "021" "021" "0221" "021" "021" "01" "021" "021" "0222"
#> SRR2140041 SRR2140036 SRR2140084 SRR2139978 SRR2139996 SRR2140017 SRR2140060 SRR2140058 SRR2140052
#> "0222" "01" "0221" "021" "021" "021" "021" "021" "021"
#> SRR2140025 SRR2140056 SRR2140021 SRR2140013 SRR2140064 SRR2139998 SRR2139992 SRR2140019 SRR2140080
#> "021" "021" "021" "021" "021" "021" "021" "021" "0222"
#> SRR2140038 SRR2140045 SRR2140032 SRR2139981 SRR2140000 SRR2140077 SRR2139986 SRR2140070 SRR2140007
#> "03" "021" "021" "01" "021" "0222" "021" "021" "021"
#> SRR2140048 SRR2140035 SRR2140042 SRR2140063 SRR2140014 SRR2139995 SRR2140069 SRR2140026 SRR2140051
#> "021" "01" "021" "0221" "021" "01" "01" "021" "021"
#> SRR2140061 SRR2140016 SRR2139979 SRR2139997 SRR2140085 SRR2140024 SRR2140053 SRR2140059 SRR2140078
#> "021" "0221" "021" "0221" "0222" "021" "021" "01" "0222"
#> SRR2139984 SRR2140072 SRR2140005 SRR2140037 SRR2140040 SRR2140047 SRR2140030 SRR2140008 SRR2139983
#> "021" "01" "021" "03" "01" "0221" "021" "01" "021"
#> SRR2139989 SRR2140002 SRR2140075 SRR2140054 SRR2140023 SRR2140029 SRR2140011 SRR2140066 SRR2139990
#> "021" "021" "021" "0222" "021" "021" "021" "021" "021"
#> SRR2140082 SRR2140086 SRR2140068 SRR2139994 SRR2140015 SRR2140062 SRR2140050 SRR2140027 SRR2140006
#> "0221" "0222" "021" "021" "01" "0221" "021" "01" "021"
#> SRR2140071 SRR2139987 SRR2140043 SRR2140034 SRR2140049 SRR2140033 SRR2140044 SRR2140039 SRR2140076
#> "01" "021" "021" "021" "021" "021" "021" "01" "0222"
#> SRR2140001 SRR2139980 SRR2140020 SRR2140057 SRR2140018 SRR2140081 SRR2139993 SRR2139999 SRR2139977
#> "021" "021" "021" "021" "0221" "0222" "021" "021" "021"
#> SRR2140065 SRR2140012 SRR2139847 SRR2139830 SRR2139787 SRR2139769 SRR2139680 SRR2139714 SRR2139763
#> "021" "021" "0222" "01" "04" "04" "04" "04" "04"
#> SRR2139808 SRR2139802 SRR2139751 SRR2139726 SRR2139854 SRR2139823 SRR2139829 SRR2139693 SRR2139707
#> "04" "0221" "0221" "01" "0221" "01" "03" "01" "04"
#> SRR2139770 SRR2139699 SRR2139677 SRR2139794 SRR2139811 SRR2139742 SRR2139735 SRR2139748 SRR2139732
#> "0221" "04" "04" "04" "01" "04" "01" "04" "04"
#> SRR2139745 SRR2139738 SRR2139816 SRR2139799 SRR2139777 SRR2139700 SRR2139694 SRR2139793 SRR2139670
#> "04" "04" "04" "04" "04" "04" "01" "01" "01"
#> SRR2139824 SRR2139853 SRR2139721 SRR2139756 SRR2139805 SRR2139719 SRR2139780 SRR2139764 SRR2139713
#> "01" "0221" "0222" "01" "01" "04" "01" "01" "04"
#> SRR2139687 SRR2139669 SRR2139837 SRR2139840 SRR2139760 SRR2139683 SRR2139717 SRR2139784 SRR2139689
#> "01" "021" "04" "01" "01" "04" "04" "01" "04"
#> SRR2139833 SRR2139844 SRR2139839 SRR2139725 SRR2139752 SRR2139758 SRR2139801 SRR2139779 SRR2139797
#> "04" "0221" "01" "04" "04" "04" "0221" "01" "01"
#> SRR2139674 SRR2139773 SRR2139690 SRR2139704 SRR2139820 SRR2139857 SRR2139736 SRR2139741 SRR2139818
#> "01" "01" "03" "0221" "04" "04" "04" "04" "01"
#> SRR2139812 SRR2139815 SRR2139746 SRR2139731 SRR2139850 SRR2139827 SRR2139673 SRR2139790 SRR2139709
#> "021" "01" "021" "01" "0221" "01" "01" "01" "01"
#> SRR2139679 SRR2139703 SRR2139697 SRR2139774 SRR2139806 SRR2139755 SRR2139722 SRR2139728 SRR2139843
#> "01" "01" "01" "04" "04" "04" "04" "04" "0222"
#> SRR2139834 SRR2139849 SRR2139710 SRR2139684 SRR2139767 SRR2139789 SRR2139783 SRR2139757 SRR2139720
#> "01" "0221" "04" "021" "03" "03" "01" "03" "04"
#> SRR2139804 SRR2139712 SRR2139686 SRR2139765 SRR2139718 SRR2139781 SRR2139841 SRR2139836 SRR2139739
#> "01" "03" "01" "01" "01" "04" "01" "01" "01"
#> SRR2139744 SRR2139733 SRR2139817 SRR2139671 SRR2139792 SRR2139798 SRR2139701 SRR2139695 SRR2139776
#> "04" "01" "04" "01" "04" "04" "04" "04" "01"
#> SRR2139858 SRR2139852 SRR2139825 SRR2139828 SRR2139822 SRR2139855 SRR2139698 SRR2139795 SRR2139676
#> "04" "0221" "03" "03" "01" "0221" "0221" "04" "04"
#> SRR2139771 SRR2139692 SRR2139706 SRR2139810 SRR2139749 SRR2139734 SRR2139743 SRR2139831 SRR2139846
#> "01" "01" "04" "01" "04" "01" "04" "03" "0221"
#> SRR2139762 SRR2139681 SRR2139715 SRR2139786 SRR2139768 SRR2139803 SRR2139809 SRR2139727 SRR2139750
#> "01" "01" "01" "04" "04" "01" "01" "04" "04"
#> SRR2139807 SRR2139729 SRR2139723 SRR2139754 SRR2139848 SRR2139835 SRR2139842 SRR2139782 SRR2139766
#> "01" "0222" "01" "01" "04" "01" "0222" "04" "03"
#> SRR2139711 SRR2139685 SRR2139788 SRR2139814 SRR2139730 SRR2139747 SRR2139826 SRR2139851 SRR2139678
#> "04" "04" "04" "01" "01" "01" "01" "0221" "01"
#> SRR2139775 SRR2139702 SRR2139696 SRR2139791 SRR2139672 SRR2139708 SRR2139691 SRR2139705 SRR2139772
#> "04" "01" "01" "03" "01" "03" "01" "01" "01"
#> SRR2139778 SRR2139675 SRR2139796 SRR2139856 SRR2139821 SRR2139740 SRR2139737 SRR2139813 SRR2139819
#> "04" "04" "04" "04" "01" "04" "01" "0221" "04"
#> SRR2139785 SRR2139688 SRR2139682 SRR2139716 SRR2139761 SRR2139838 SRR2139845 SRR2139832 SRR2139759
#> "04" "01" "01" "04" "04" "01" "0221" "01" "04"
#> SRR2139753 SRR2139724 SRR2139800 SRR2139306 SRR2139371 SRR2139343 SRR2139334 SRR2139349 SRR2139368
#> "01" "01" "01" "03" "03" "03" "03" "03" "03"
#> SRR2139315 SRR2139362 SRR2139350 SRR2139327 SRR2139320 SRR2139357 SRR2139318 SRR2139381 SRR2139365
#> "03" "03" "03" "03" "03" "03" "03" "03" "03"
#> SRR2139312 SRR2139333 SRR2139344 SRR2139339 SRR2139376 SRR2139378 SRR2139372 SRR2139337 SRR2139340
#> "03" "0222" "03" "03" "03" "03" "03" "03" "03"
#> SRR2139361 SRR2139316 SRR2139324 SRR2139353 SRR2139359 SRR2139354 SRR2139323 SRR2139329 SRR2139311
#> "03" "03" "03" "03" "03" "03" "03" "03" "03"
#> SRR2139366 SRR2139382 SRR2139347 SRR2139330 SRR2139308 SRR2139375 SRR2139338 SRR2139345 SRR2139332
#> "03" "03" "03" "03" "03" "03" "03" "03" "03"
#> SRR2139377 SRR2139356 SRR2139321 SRR2139313 SRR2139364 SRR2139319 SRR2139380 SRR2139363 SRR2139314
#> "03" "03" "03" "03" "03" "03" "03" "03" "03"
#> SRR2139369 SRR2139326 SRR2139351 SRR2139370 SRR2139307 SRR2139348 SRR2139335 SRR2139342 SRR2139331
#> "03" "03" "03" "03" "03" "03" "03" "03" "03"
#> SRR2139346 SRR2139374 SRR2139309 SRR2139328 SRR2139322 SRR2139355 SRR2139383 SRR2139367 SRR2139310
#> "03" "03" "03" "03" "03" "03" "0222" "03" "03"
#> SRR2139384 SRR2139317 SRR2139360 SRR2139358 SRR2139352 SRR2139325 SRR2139373 SRR2139379 SRR2139341
#> "0222" "03" "03" "03" "03" "0222" "03" "03" "03"
#> SRR2139336
#> "03"
get_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 1267))
#> SRR2140028 SRR2140022 SRR2140055 SRR2140083 SRR2139991 SRR2140067 SRR2140010 SRR2140031 SRR2140046
#> "021" "021" "022" "022" "021" "021" "021" "021" "022"
#> SRR2140074 SRR2140003 SRR2139988 SRR2139982 SRR2140009 SRR2140004 SRR2140073 SRR2139985 SRR2140079
#> "021" "021" "022" "021" "021" "01" "021" "021" "022"
#> SRR2140041 SRR2140036 SRR2140084 SRR2139978 SRR2139996 SRR2140017 SRR2140060 SRR2140058 SRR2140052
#> "022" "01" "022" "021" "021" "021" "021" "021" "021"
#> SRR2140025 SRR2140056 SRR2140021 SRR2140013 SRR2140064 SRR2139998 SRR2139992 SRR2140019 SRR2140080
#> "021" "021" "021" "021" "021" "021" "021" "021" "022"
#> SRR2140038 SRR2140045 SRR2140032 SRR2139981 SRR2140000 SRR2140077 SRR2139986 SRR2140070 SRR2140007
#> "03" "021" "021" "01" "021" "022" "021" "021" "021"
#> SRR2140048 SRR2140035 SRR2140042 SRR2140063 SRR2140014 SRR2139995 SRR2140069 SRR2140026 SRR2140051
#> "021" "01" "021" "022" "021" "01" "01" "021" "021"
#> SRR2140061 SRR2140016 SRR2139979 SRR2139997 SRR2140085 SRR2140024 SRR2140053 SRR2140059 SRR2140078
#> "021" "022" "021" "022" "022" "021" "021" "01" "022"
#> SRR2139984 SRR2140072 SRR2140005 SRR2140037 SRR2140040 SRR2140047 SRR2140030 SRR2140008 SRR2139983
#> "021" "01" "021" "03" "01" "022" "021" "01" "021"
#> SRR2139989 SRR2140002 SRR2140075 SRR2140054 SRR2140023 SRR2140029 SRR2140011 SRR2140066 SRR2139990
#> "021" "021" "021" "022" "021" "021" "021" "021" "021"
#> SRR2140082 SRR2140086 SRR2140068 SRR2139994 SRR2140015 SRR2140062 SRR2140050 SRR2140027 SRR2140006
#> "022" "022" "021" "021" "01" "022" "021" "01" "021"
#> SRR2140071 SRR2139987 SRR2140043 SRR2140034 SRR2140049 SRR2140033 SRR2140044 SRR2140039 SRR2140076
#> "01" "021" "021" "021" "021" "021" "021" "01" "022"
#> SRR2140001 SRR2139980 SRR2140020 SRR2140057 SRR2140018 SRR2140081 SRR2139993 SRR2139999 SRR2139977
#> "021" "021" "021" "021" "022" "022" "021" "021" "021"
#> SRR2140065 SRR2140012 SRR2139847 SRR2139830 SRR2139787 SRR2139769 SRR2139680 SRR2139714 SRR2139763
#> "021" "021" "022" "01" "04" "04" "04" "04" "04"
#> SRR2139808 SRR2139802 SRR2139751 SRR2139726 SRR2139854 SRR2139823 SRR2139829 SRR2139693 SRR2139707
#> "04" "022" "022" "01" "022" "01" "03" "01" "04"
#> SRR2139770 SRR2139699 SRR2139677 SRR2139794 SRR2139811 SRR2139742 SRR2139735 SRR2139748 SRR2139732
#> "022" "04" "04" "04" "01" "04" "01" "04" "04"
#> SRR2139745 SRR2139738 SRR2139816 SRR2139799 SRR2139777 SRR2139700 SRR2139694 SRR2139793 SRR2139670
#> "04" "04" "04" "04" "04" "04" "01" "01" "01"
#> SRR2139824 SRR2139853 SRR2139721 SRR2139756 SRR2139805 SRR2139719 SRR2139780 SRR2139764 SRR2139713
#> "01" "022" "022" "01" "01" "04" "01" "01" "04"
#> SRR2139687 SRR2139669 SRR2139837 SRR2139840 SRR2139760 SRR2139683 SRR2139717 SRR2139784 SRR2139689
#> "01" "021" "04" "01" "01" "04" "04" "01" "04"
#> SRR2139833 SRR2139844 SRR2139839 SRR2139725 SRR2139752 SRR2139758 SRR2139801 SRR2139779 SRR2139797
#> "04" "022" "01" "04" "04" "04" "022" "01" "01"
#> SRR2139674 SRR2139773 SRR2139690 SRR2139704 SRR2139820 SRR2139857 SRR2139736 SRR2139741 SRR2139818
#> "01" "01" "03" "022" "04" "04" "04" "04" "01"
#> SRR2139812 SRR2139815 SRR2139746 SRR2139731 SRR2139850 SRR2139827 SRR2139673 SRR2139790 SRR2139709
#> "021" "01" "021" "01" "022" "01" "01" "01" "01"
#> SRR2139679 SRR2139703 SRR2139697 SRR2139774 SRR2139806 SRR2139755 SRR2139722 SRR2139728 SRR2139843
#> "01" "01" "01" "04" "04" "04" "04" "04" "022"
#> SRR2139834 SRR2139849 SRR2139710 SRR2139684 SRR2139767 SRR2139789 SRR2139783 SRR2139757 SRR2139720
#> "01" "022" "04" "021" "03" "03" "01" "03" "04"
#> SRR2139804 SRR2139712 SRR2139686 SRR2139765 SRR2139718 SRR2139781 SRR2139841 SRR2139836 SRR2139739
#> "01" "03" "01" "01" "01" "04" "01" "01" "01"
#> SRR2139744 SRR2139733 SRR2139817 SRR2139671 SRR2139792 SRR2139798 SRR2139701 SRR2139695 SRR2139776
#> "04" "01" "04" "01" "04" "04" "04" "04" "01"
#> SRR2139858 SRR2139852 SRR2139825 SRR2139828 SRR2139822 SRR2139855 SRR2139698 SRR2139795 SRR2139676
#> "04" "022" "03" "03" "01" "022" "022" "04" "04"
#> SRR2139771 SRR2139692 SRR2139706 SRR2139810 SRR2139749 SRR2139734 SRR2139743 SRR2139831 SRR2139846
#> "01" "01" "04" "01" "04" "01" "04" "03" "022"
#> SRR2139762 SRR2139681 SRR2139715 SRR2139786 SRR2139768 SRR2139803 SRR2139809 SRR2139727 SRR2139750
#> "01" "01" "01" "04" "04" "01" "01" "04" "04"
#> SRR2139807 SRR2139729 SRR2139723 SRR2139754 SRR2139848 SRR2139835 SRR2139842 SRR2139782 SRR2139766
#> "01" "022" "01" "01" "04" "01" "022" "04" "03"
#> SRR2139711 SRR2139685 SRR2139788 SRR2139814 SRR2139730 SRR2139747 SRR2139826 SRR2139851 SRR2139678
#> "04" "04" "04" "01" "01" "01" "01" "022" "01"
#> SRR2139775 SRR2139702 SRR2139696 SRR2139791 SRR2139672 SRR2139708 SRR2139691 SRR2139705 SRR2139772
#> "04" "01" "01" "03" "01" "03" "01" "01" "01"
#> SRR2139778 SRR2139675 SRR2139796 SRR2139856 SRR2139821 SRR2139740 SRR2139737 SRR2139813 SRR2139819
#> "04" "04" "04" "04" "01" "04" "01" "022" "04"
#> SRR2139785 SRR2139688 SRR2139682 SRR2139716 SRR2139761 SRR2139838 SRR2139845 SRR2139832 SRR2139759
#> "04" "01" "01" "04" "04" "01" "022" "01" "04"
#> SRR2139753 SRR2139724 SRR2139800 SRR2139306 SRR2139371 SRR2139343 SRR2139334 SRR2139349 SRR2139368
#> "01" "01" "01" "03" "03" "03" "03" "03" "03"
#> SRR2139315 SRR2139362 SRR2139350 SRR2139327 SRR2139320 SRR2139357 SRR2139318 SRR2139381 SRR2139365
#> "03" "03" "03" "03" "03" "03" "03" "03" "03"
#> SRR2139312 SRR2139333 SRR2139344 SRR2139339 SRR2139376 SRR2139378 SRR2139372 SRR2139337 SRR2139340
#> "03" "022" "03" "03" "03" "03" "03" "03" "03"
#> SRR2139361 SRR2139316 SRR2139324 SRR2139353 SRR2139359 SRR2139354 SRR2139323 SRR2139329 SRR2139311
#> "03" "03" "03" "03" "03" "03" "03" "03" "03"
#> SRR2139366 SRR2139382 SRR2139347 SRR2139330 SRR2139308 SRR2139375 SRR2139338 SRR2139345 SRR2139332
#> "03" "03" "03" "03" "03" "03" "03" "03" "03"
#> SRR2139377 SRR2139356 SRR2139321 SRR2139313 SRR2139364 SRR2139319 SRR2139380 SRR2139363 SRR2139314
#> "03" "03" "03" "03" "03" "03" "03" "03" "03"
#> SRR2139369 SRR2139326 SRR2139351 SRR2139370 SRR2139307 SRR2139348 SRR2139335 SRR2139342 SRR2139331
#> "03" "03" "03" "03" "03" "03" "03" "03" "03"
#> SRR2139346 SRR2139374 SRR2139309 SRR2139328 SRR2139322 SRR2139355 SRR2139383 SRR2139367 SRR2139310
#> "03" "03" "03" "03" "03" "03" "022" "03" "03"
#> SRR2139384 SRR2139317 SRR2139360 SRR2139358 SRR2139352 SRR2139325 SRR2139373 SRR2139379 SRR2139341
#> "022" "03" "03" "03" "03" "022" "03" "03" "03"
#> SRR2139336
#> "03"
get_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 5059))
#> SRR2140028 SRR2140022 SRR2140055 SRR2140083 SRR2139991 SRR2140067 SRR2140010 SRR2140031 SRR2140046
#> "02" "02" "02" "02" "02" "02" "02" "02" "02"
#> SRR2140074 SRR2140003 SRR2139988 SRR2139982 SRR2140009 SRR2140004 SRR2140073 SRR2139985 SRR2140079
#> "02" "02" "02" "02" "02" "01" "02" "02" "02"
#> SRR2140041 SRR2140036 SRR2140084 SRR2139978 SRR2139996 SRR2140017 SRR2140060 SRR2140058 SRR2140052
#> "02" "01" "02" "02" "02" "02" "02" "02" "02"
#> SRR2140025 SRR2140056 SRR2140021 SRR2140013 SRR2140064 SRR2139998 SRR2139992 SRR2140019 SRR2140080
#> "02" "02" "02" "02" "02" "02" "02" "02" "02"
#> SRR2140038 SRR2140045 SRR2140032 SRR2139981 SRR2140000 SRR2140077 SRR2139986 SRR2140070 SRR2140007
#> "03" "02" "02" "01" "02" "02" "02" "02" "02"
#> SRR2140048 SRR2140035 SRR2140042 SRR2140063 SRR2140014 SRR2139995 SRR2140069 SRR2140026 SRR2140051
#> "02" "01" "02" "02" "02" "01" "01" "02" "02"
#> SRR2140061 SRR2140016 SRR2139979 SRR2139997 SRR2140085 SRR2140024 SRR2140053 SRR2140059 SRR2140078
#> "02" "02" "02" "02" "02" "02" "02" "01" "02"
#> SRR2139984 SRR2140072 SRR2140005 SRR2140037 SRR2140040 SRR2140047 SRR2140030 SRR2140008 SRR2139983
#> "02" "01" "02" "03" "01" "02" "02" "01" "02"
#> SRR2139989 SRR2140002 SRR2140075 SRR2140054 SRR2140023 SRR2140029 SRR2140011 SRR2140066 SRR2139990
#> "02" "02" "02" "02" "02" "02" "02" "02" "02"
#> SRR2140082 SRR2140086 SRR2140068 SRR2139994 SRR2140015 SRR2140062 SRR2140050 SRR2140027 SRR2140006
#> "02" "02" "02" "02" "01" "02" "02" "01" "02"
#> SRR2140071 SRR2139987 SRR2140043 SRR2140034 SRR2140049 SRR2140033 SRR2140044 SRR2140039 SRR2140076
#> "01" "02" "02" "02" "02" "02" "02" "01" "02"
#> SRR2140001 SRR2139980 SRR2140020 SRR2140057 SRR2140018 SRR2140081 SRR2139993 SRR2139999 SRR2139977
#> "02" "02" "02" "02" "02" "02" "02" "02" "02"
#> SRR2140065 SRR2140012 SRR2139847 SRR2139830 SRR2139787 SRR2139769 SRR2139680 SRR2139714 SRR2139763
#> "02" "02" "02" "01" "04" "04" "04" "04" "04"
#> SRR2139808 SRR2139802 SRR2139751 SRR2139726 SRR2139854 SRR2139823 SRR2139829 SRR2139693 SRR2139707
#> "04" "02" "02" "01" "02" "01" "03" "01" "04"
#> SRR2139770 SRR2139699 SRR2139677 SRR2139794 SRR2139811 SRR2139742 SRR2139735 SRR2139748 SRR2139732
#> "02" "04" "04" "04" "01" "04" "01" "04" "04"
#> SRR2139745 SRR2139738 SRR2139816 SRR2139799 SRR2139777 SRR2139700 SRR2139694 SRR2139793 SRR2139670
#> "04" "04" "04" "04" "04" "04" "01" "01" "01"
#> SRR2139824 SRR2139853 SRR2139721 SRR2139756 SRR2139805 SRR2139719 SRR2139780 SRR2139764 SRR2139713
#> "01" "02" "02" "01" "01" "04" "01" "01" "04"
#> SRR2139687 SRR2139669 SRR2139837 SRR2139840 SRR2139760 SRR2139683 SRR2139717 SRR2139784 SRR2139689
#> "01" "02" "04" "01" "01" "04" "04" "01" "04"
#> SRR2139833 SRR2139844 SRR2139839 SRR2139725 SRR2139752 SRR2139758 SRR2139801 SRR2139779 SRR2139797
#> "04" "02" "01" "04" "04" "04" "02" "01" "01"
#> SRR2139674 SRR2139773 SRR2139690 SRR2139704 SRR2139820 SRR2139857 SRR2139736 SRR2139741 SRR2139818
#> "01" "01" "03" "02" "04" "04" "04" "04" "01"
#> SRR2139812 SRR2139815 SRR2139746 SRR2139731 SRR2139850 SRR2139827 SRR2139673 SRR2139790 SRR2139709
#> "02" "01" "02" "01" "02" "01" "01" "01" "01"
#> SRR2139679 SRR2139703 SRR2139697 SRR2139774 SRR2139806 SRR2139755 SRR2139722 SRR2139728 SRR2139843
#> "01" "01" "01" "04" "04" "04" "04" "04" "02"
#> SRR2139834 SRR2139849 SRR2139710 SRR2139684 SRR2139767 SRR2139789 SRR2139783 SRR2139757 SRR2139720
#> "01" "02" "04" "02" "03" "03" "01" "03" "04"
#> SRR2139804 SRR2139712 SRR2139686 SRR2139765 SRR2139718 SRR2139781 SRR2139841 SRR2139836 SRR2139739
#> "01" "03" "01" "01" "01" "04" "01" "01" "01"
#> SRR2139744 SRR2139733 SRR2139817 SRR2139671 SRR2139792 SRR2139798 SRR2139701 SRR2139695 SRR2139776
#> "04" "01" "04" "01" "04" "04" "04" "04" "01"
#> SRR2139858 SRR2139852 SRR2139825 SRR2139828 SRR2139822 SRR2139855 SRR2139698 SRR2139795 SRR2139676
#> "04" "02" "03" "03" "01" "02" "02" "04" "04"
#> SRR2139771 SRR2139692 SRR2139706 SRR2139810 SRR2139749 SRR2139734 SRR2139743 SRR2139831 SRR2139846
#> "01" "01" "04" "01" "04" "01" "04" "03" "02"
#> SRR2139762 SRR2139681 SRR2139715 SRR2139786 SRR2139768 SRR2139803 SRR2139809 SRR2139727 SRR2139750
#> "01" "01" "01" "04" "04" "01" "01" "04" "04"
#> SRR2139807 SRR2139729 SRR2139723 SRR2139754 SRR2139848 SRR2139835 SRR2139842 SRR2139782 SRR2139766
#> "01" "02" "01" "01" "04" "01" "02" "04" "03"
#> SRR2139711 SRR2139685 SRR2139788 SRR2139814 SRR2139730 SRR2139747 SRR2139826 SRR2139851 SRR2139678
#> "04" "04" "04" "01" "01" "01" "01" "02" "01"
#> SRR2139775 SRR2139702 SRR2139696 SRR2139791 SRR2139672 SRR2139708 SRR2139691 SRR2139705 SRR2139772
#> "04" "01" "01" "03" "01" "03" "01" "01" "01"
#> SRR2139778 SRR2139675 SRR2139796 SRR2139856 SRR2139821 SRR2139740 SRR2139737 SRR2139813 SRR2139819
#> "04" "04" "04" "04" "01" "04" "01" "02" "04"
#> SRR2139785 SRR2139688 SRR2139682 SRR2139716 SRR2139761 SRR2139838 SRR2139845 SRR2139832 SRR2139759
#> "04" "01" "01" "04" "04" "01" "02" "01" "04"
#> SRR2139753 SRR2139724 SRR2139800 SRR2139306 SRR2139371 SRR2139343 SRR2139334 SRR2139349 SRR2139368
#> "01" "01" "01" "03" "03" "03" "03" "03" "03"
#> SRR2139315 SRR2139362 SRR2139350 SRR2139327 SRR2139320 SRR2139357 SRR2139318 SRR2139381 SRR2139365
#> "03" "03" "03" "03" "03" "03" "03" "03" "03"
#> SRR2139312 SRR2139333 SRR2139344 SRR2139339 SRR2139376 SRR2139378 SRR2139372 SRR2139337 SRR2139340
#> "03" "02" "03" "03" "03" "03" "03" "03" "03"
#> SRR2139361 SRR2139316 SRR2139324 SRR2139353 SRR2139359 SRR2139354 SRR2139323 SRR2139329 SRR2139311
#> "03" "03" "03" "03" "03" "03" "03" "03" "03"
#> SRR2139366 SRR2139382 SRR2139347 SRR2139330 SRR2139308 SRR2139375 SRR2139338 SRR2139345 SRR2139332
#> "03" "03" "03" "03" "03" "03" "03" "03" "03"
#> SRR2139377 SRR2139356 SRR2139321 SRR2139313 SRR2139364 SRR2139319 SRR2139380 SRR2139363 SRR2139314
#> "03" "03" "03" "03" "03" "03" "03" "03" "03"
#> SRR2139369 SRR2139326 SRR2139351 SRR2139370 SRR2139307 SRR2139348 SRR2139335 SRR2139342 SRR2139331
#> "03" "03" "03" "03" "03" "03" "03" "03" "03"
#> SRR2139346 SRR2139374 SRR2139309 SRR2139328 SRR2139322 SRR2139355 SRR2139383 SRR2139367 SRR2139310
#> "03" "03" "03" "03" "03" "03" "02" "03" "03"
#> SRR2139384 SRR2139317 SRR2139360 SRR2139358 SRR2139352 SRR2139325 SRR2139373 SRR2139379 SRR2139341
#> "02" "03" "03" "03" "03" "02" "03" "03" "03"
#> SRR2139336
#> "03"
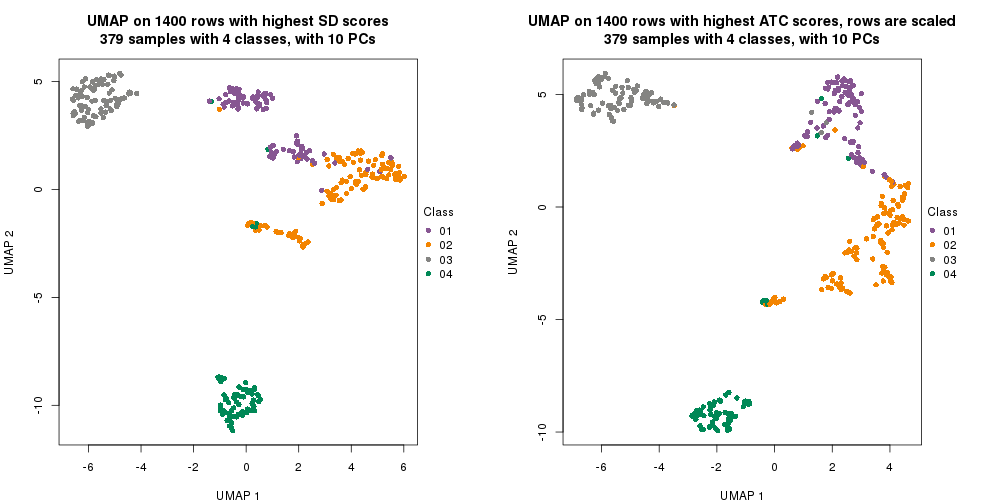
Heatmaps of the top rows:
top_rows_heatmap(res_rh)
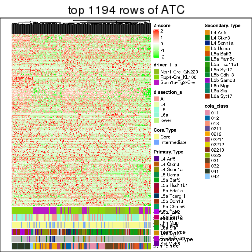
Top rows on each node:
top_rows_overlap(res_rh, method = "upset")
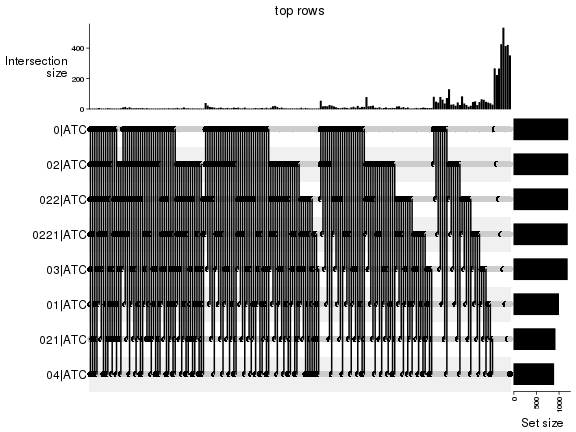
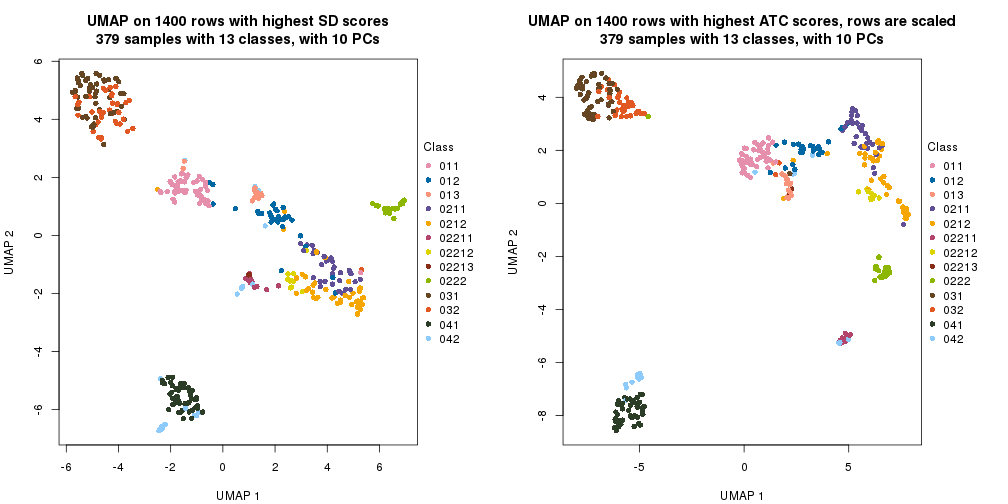
UMAP plot which shows how samples are separated.
par(mfrow = c(1, 2))
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 305),
method = "UMAP", top_value_method = "SD", top_n = 1400, scale_rows = FALSE)
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 305),
method = "UMAP", top_value_method = "ATC", top_n = 1400, scale_rows = TRUE)
par(mfrow = c(1, 2))
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 365),
method = "UMAP", top_value_method = "SD", top_n = 1400, scale_rows = FALSE)
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 365),
method = "UMAP", top_value_method = "ATC", top_n = 1400, scale_rows = TRUE)
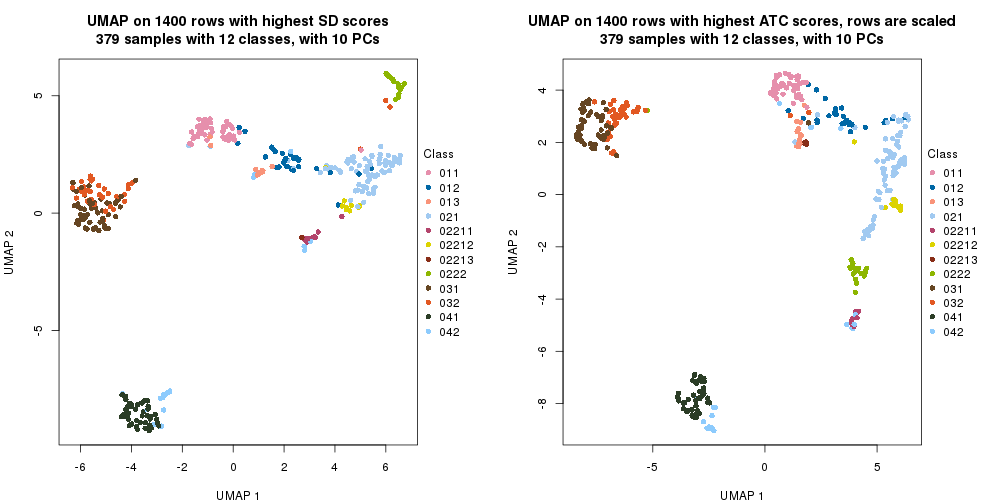
par(mfrow = c(1, 2))
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 404),
method = "UMAP", top_value_method = "SD", top_n = 1400, scale_rows = FALSE)
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 404),
method = "UMAP", top_value_method = "ATC", top_n = 1400, scale_rows = TRUE)
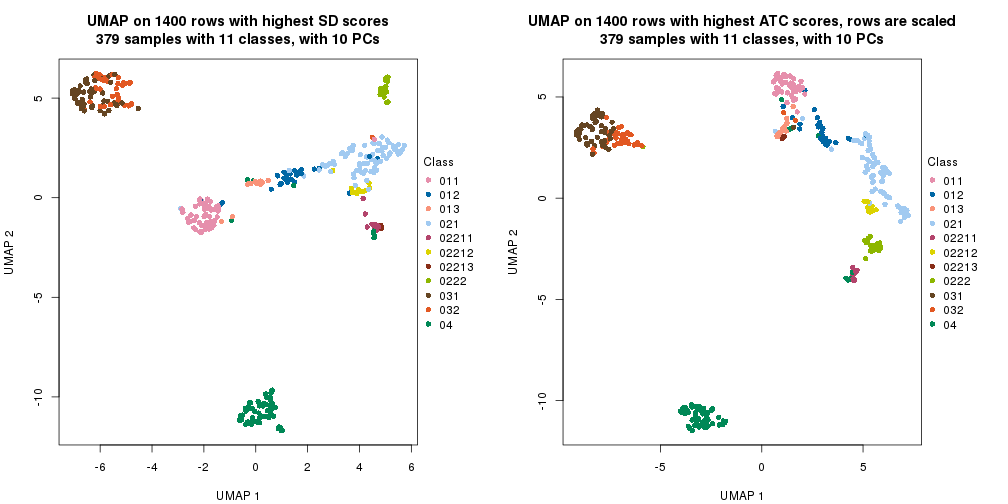
par(mfrow = c(1, 2))
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 614),
method = "UMAP", top_value_method = "SD", top_n = 1400, scale_rows = FALSE)
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 614),
method = "UMAP", top_value_method = "ATC", top_n = 1400, scale_rows = TRUE)
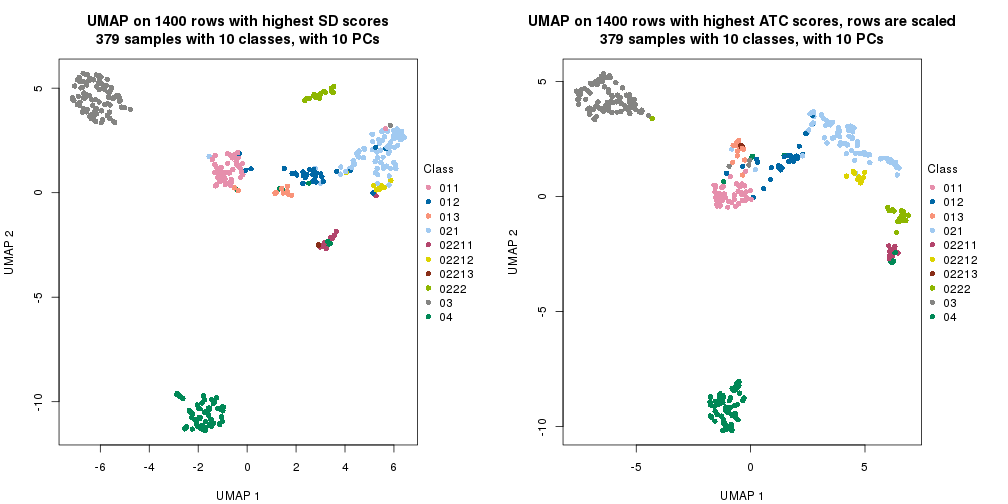
par(mfrow = c(1, 2))
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 703),
method = "UMAP", top_value_method = "SD", top_n = 1400, scale_rows = FALSE)
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 703),
method = "UMAP", top_value_method = "ATC", top_n = 1400, scale_rows = TRUE)
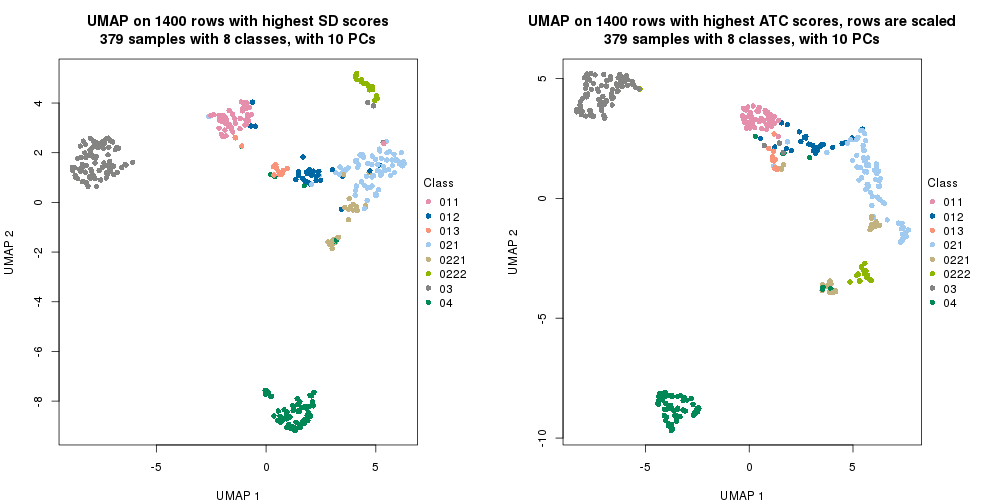
par(mfrow = c(1, 2))
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 844),
method = "UMAP", top_value_method = "SD", top_n = 1400, scale_rows = FALSE)
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 844),
method = "UMAP", top_value_method = "ATC", top_n = 1400, scale_rows = TRUE)
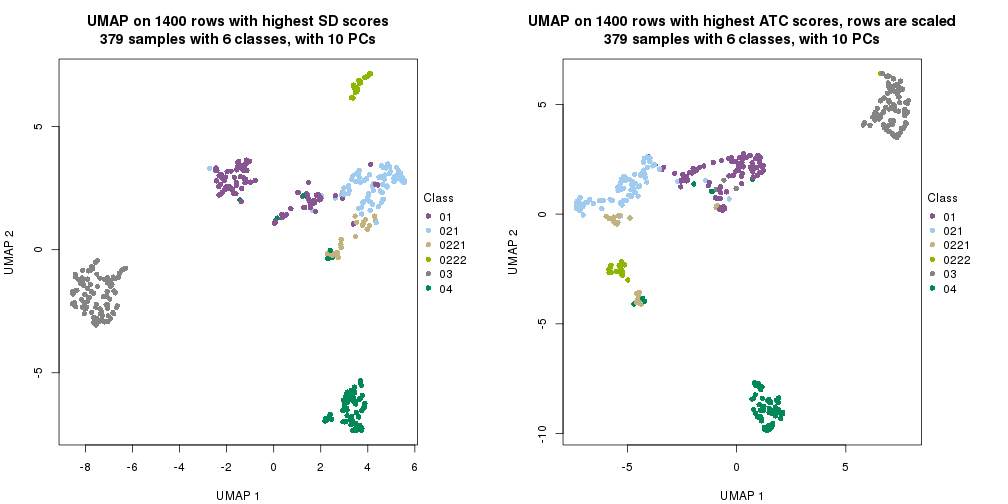
par(mfrow = c(1, 2))
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 1267),
method = "UMAP", top_value_method = "SD", top_n = 1400, scale_rows = FALSE)
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 1267),
method = "UMAP", top_value_method = "ATC", top_n = 1400, scale_rows = TRUE)
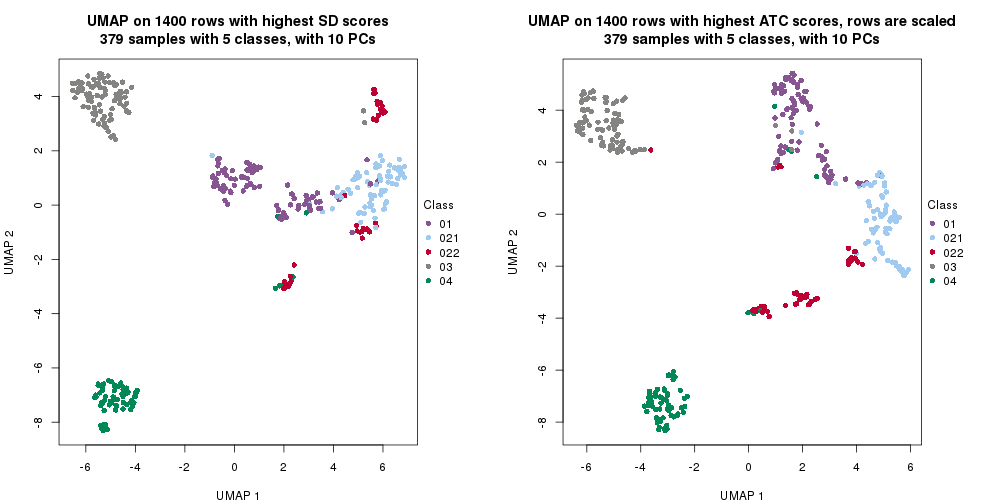
par(mfrow = c(1, 2))
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 5059),
method = "UMAP", top_value_method = "SD", top_n = 1400, scale_rows = FALSE)
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 5059),
method = "UMAP", top_value_method = "ATC", top_n = 1400, scale_rows = TRUE)
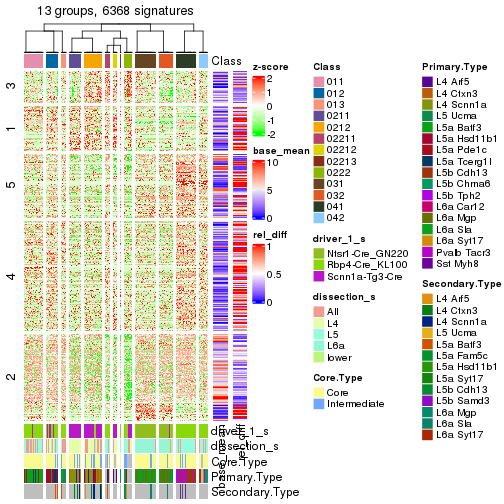
Signatures on the heatmap are the union of all signatures found on every node on the hierarchy. The number of k-means on rows are automatically selected by the function.
get_signatures(res_rh, merge_node = merge_node_param(min_n_signatures = 305))
get_signatures(res_rh, merge_node = merge_node_param(min_n_signatures = 365))
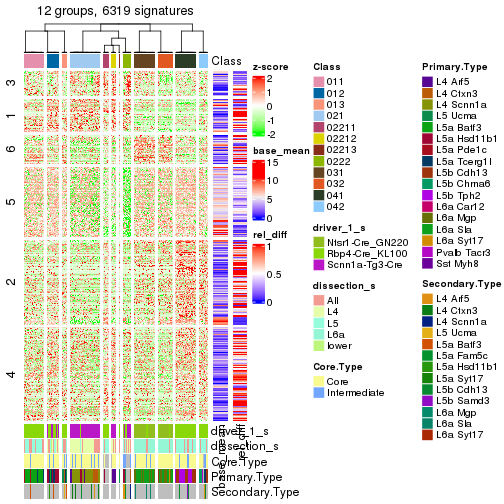
get_signatures(res_rh, merge_node = merge_node_param(min_n_signatures = 404))
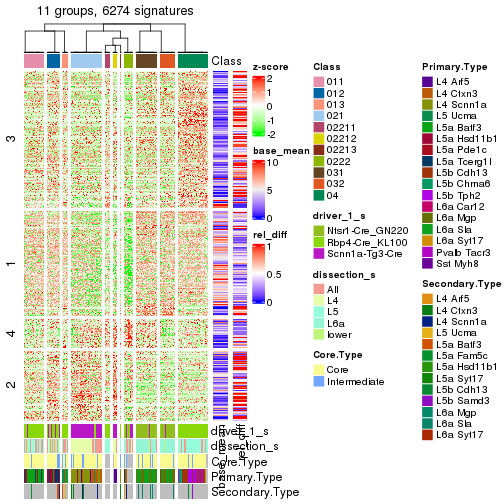
get_signatures(res_rh, merge_node = merge_node_param(min_n_signatures = 614))
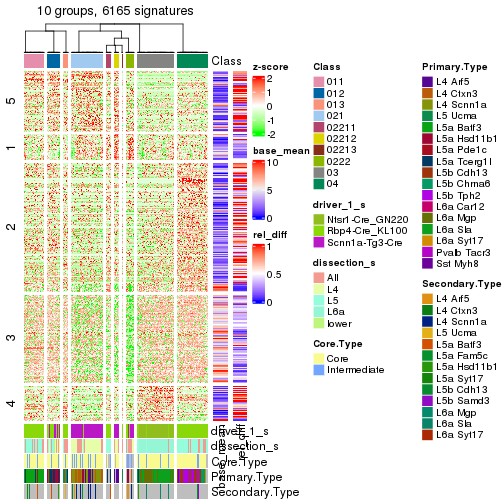
get_signatures(res_rh, merge_node = merge_node_param(min_n_signatures = 703))
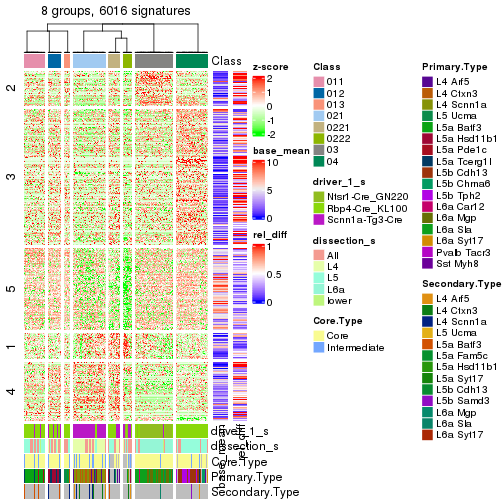
get_signatures(res_rh, merge_node = merge_node_param(min_n_signatures = 844))
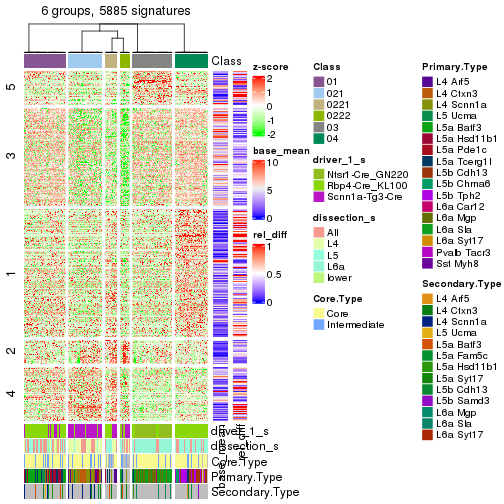
get_signatures(res_rh, merge_node = merge_node_param(min_n_signatures = 1267))
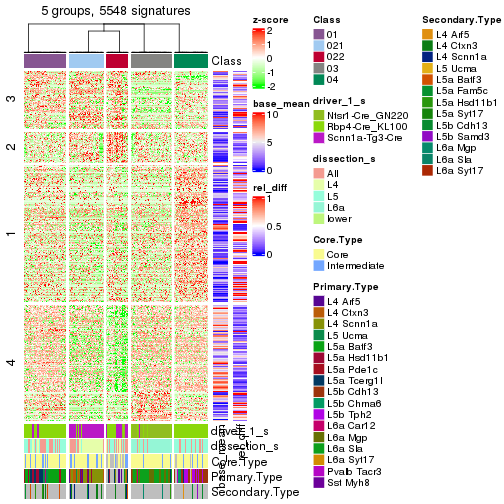
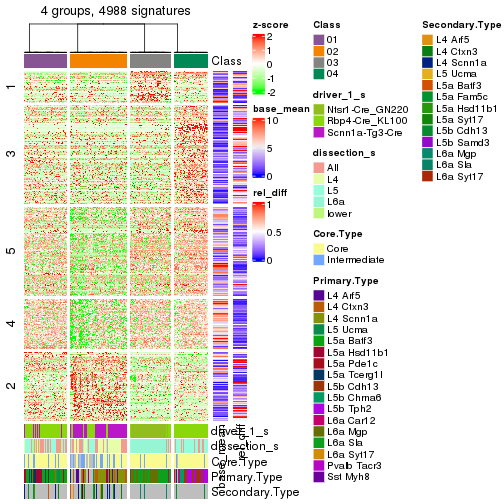
get_signatures(res_rh, merge_node = merge_node_param(min_n_signatures = 5059))
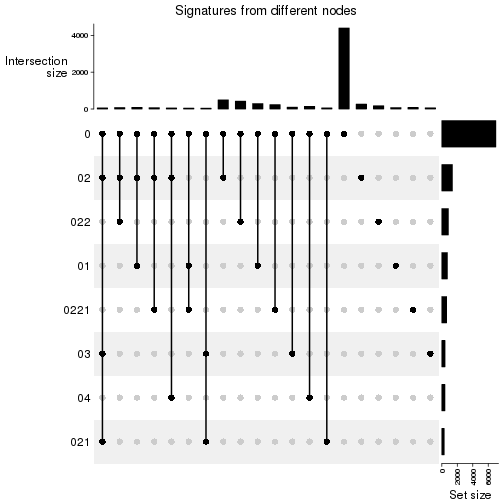
Compare signatures from different nodes:
compare_signatures(res_rh, verbose = FALSE)
If there are too many signatures, top_signatures = ... can be set to only show the
signatures with the highest FDRs. Note it only works on every node and the final signatures
are the union of all signatures of all nodes.
# code only for demonstration
# e.g. to show the top 500 most significant rows on each node.
tb = get_signature(res_rh, top_signatures = 500)
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res_rh, merge_node = merge_node_param(min_n_signatures = 305))
#> driver_1_s dissection_s Core.Type Primary.Type Secondary.Type
#> class 1.23e-102 8.78e-95 1.93e-06 6.73e-241 2.91e-09
test_to_known_factors(res_rh, merge_node = merge_node_param(min_n_signatures = 365))
#> driver_1_s dissection_s Core.Type Primary.Type Secondary.Type
#> class 7.05e-104 5.31e-89 8.91e-07 1.96e-244 1.86e-10
test_to_known_factors(res_rh, merge_node = merge_node_param(min_n_signatures = 404))
#> driver_1_s dissection_s Core.Type Primary.Type Secondary.Type
#> class 2.52e-105 6.55e-91 5.13e-07 1.22e-210 4.43e-10
test_to_known_factors(res_rh, merge_node = merge_node_param(min_n_signatures = 614))
#> driver_1_s dissection_s Core.Type Primary.Type Secondary.Type
#> class 9.89e-107 3.75e-93 2.26e-07 2.24e-214 6.59e-11
test_to_known_factors(res_rh, merge_node = merge_node_param(min_n_signatures = 703))
#> driver_1_s dissection_s Core.Type Primary.Type Secondary.Type
#> class 1.19e-103 1.57e-91 9.82e-08 6.06e-212 2.72e-13
test_to_known_factors(res_rh, merge_node = merge_node_param(min_n_signatures = 844))
#> driver_1_s dissection_s Core.Type Primary.Type Secondary.Type
#> class 5.65e-104 5.95e-90 1.41e-07 1.21e-156 1.05e-12
test_to_known_factors(res_rh, merge_node = merge_node_param(min_n_signatures = 1267))
#> driver_1_s dissection_s Core.Type Primary.Type Secondary.Type
#> class 3.25e-104 1.18e-90 0.00021 3.56e-159 8.42e-10
test_to_known_factors(res_rh, merge_node = merge_node_param(min_n_signatures = 5059))
#> driver_1_s dissection_s Core.Type Primary.Type Secondary.Type
#> class 1.25e-98 2.98e-84 0.000127 8.66e-155 4.71e-10
Child nodes: Node01 , Node02 , Node03 , Node04 .
The object with results only for a single top-value method and a single partitioning method can be extracted as:
res = res_rh["0"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4.
#> On a matrix with 11945 rows and 379 columns.
#> Top rows (1194) are extracted by 'ATC' method.
#> Subgroups are detected by 'skmeans' method.
#> Performed in total 150 partitions by row resampling.
#> Best k for subgroups seems to be 4.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_partitions"
#> [7] "compare_signatures" "consensus_heatmap" "dimension_reduction"
#> [10] "functional_enrichment" "get_anno_col" "get_anno"
#> [13] "get_classes" "get_consensus" "get_matrix"
#> [16] "get_membership" "get_param" "get_signatures"
#> [19] "get_stats" "is_best_k" "is_stable_k"
#> [22] "membership_heatmap" "ncol" "nrow"
#> [25] "plot_ecdf" "predict_classes" "rownames"
#> [28] "select_partition_number" "show" "suggest_best_k"
#> [31] "test_to_known_factors" "top_rows_heatmap"
collect_plots() function collects all the plots made from res for all k (number of subgroups)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
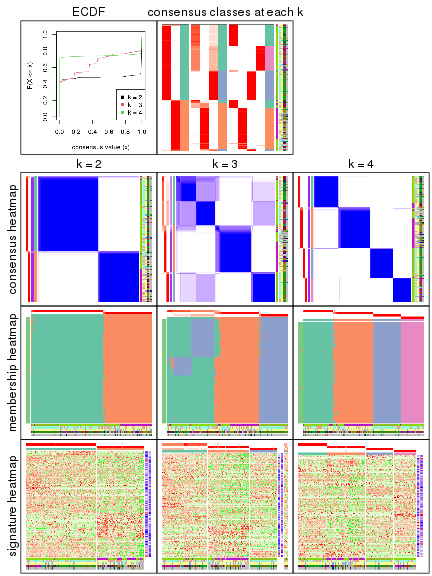
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, higher 1-PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
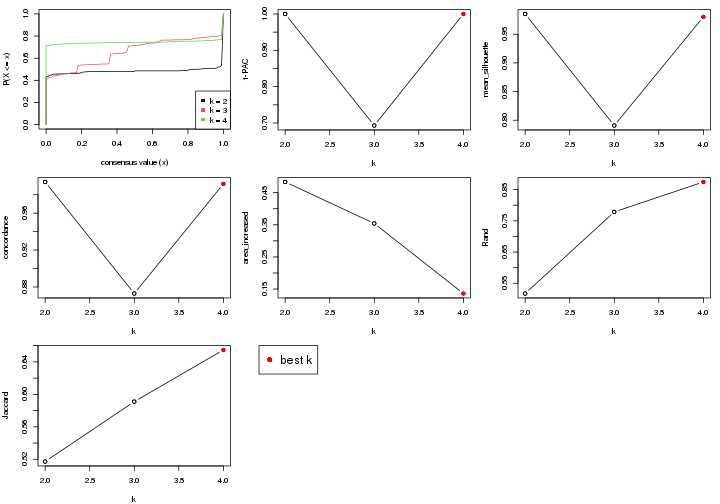
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 1.000 0.985 0.994 0.483 0.517 0.517
#> 3 3 0.693 0.791 0.873 0.354 0.779 0.591
#> 4 4 1.000 0.980 0.992 0.136 0.874 0.655
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 4
#> attr(,"optional")
#> [1] 2
There is also optional best \(k\) = 2 that is worth to check.
Following is the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall subgroup
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> SRR2140028 2 0.000 0.9924 0.00 1.00
#> SRR2140022 2 0.000 0.9924 0.00 1.00
#> SRR2140055 2 0.000 0.9924 0.00 1.00
#> SRR2140083 2 0.000 0.9924 0.00 1.00
#> SRR2139991 2 0.000 0.9924 0.00 1.00
#> SRR2140067 2 0.000 0.9924 0.00 1.00
#> SRR2140010 2 0.000 0.9924 0.00 1.00
#> SRR2140031 2 0.000 0.9924 0.00 1.00
#> SRR2140046 2 0.000 0.9924 0.00 1.00
#> SRR2140074 2 0.000 0.9924 0.00 1.00
#> SRR2140003 2 0.000 0.9924 0.00 1.00
#> SRR2139988 2 0.000 0.9924 0.00 1.00
#> SRR2139982 2 0.000 0.9924 0.00 1.00
#> SRR2140009 2 0.000 0.9924 0.00 1.00
#> SRR2140004 1 0.680 0.7810 0.82 0.18
#> SRR2140073 2 0.000 0.9924 0.00 1.00
#> SRR2139985 2 0.000 0.9924 0.00 1.00
#> SRR2140079 2 0.000 0.9924 0.00 1.00
#> SRR2140041 2 0.000 0.9924 0.00 1.00
#> SRR2140036 2 0.141 0.9736 0.02 0.98
#> SRR2140084 2 0.000 0.9924 0.00 1.00
#> SRR2139978 2 0.000 0.9924 0.00 1.00
#> SRR2139996 2 0.000 0.9924 0.00 1.00
#> SRR2140017 2 0.000 0.9924 0.00 1.00
#> SRR2140060 2 0.000 0.9924 0.00 1.00
#> SRR2140058 2 0.000 0.9924 0.00 1.00
#> SRR2140052 2 0.000 0.9924 0.00 1.00
#> SRR2140025 2 0.000 0.9924 0.00 1.00
#> SRR2140056 2 0.000 0.9924 0.00 1.00
#> SRR2140021 2 0.000 0.9924 0.00 1.00
#> SRR2140013 2 0.000 0.9924 0.00 1.00
#> SRR2140064 2 0.000 0.9924 0.00 1.00
#> SRR2139998 2 0.000 0.9924 0.00 1.00
#> SRR2139992 2 0.000 0.9924 0.00 1.00
#> SRR2140019 2 0.000 0.9924 0.00 1.00
#> SRR2140080 2 0.000 0.9924 0.00 1.00
#> SRR2140038 1 0.000 0.9945 1.00 0.00
#> SRR2140045 2 0.000 0.9924 0.00 1.00
#> SRR2140032 2 0.000 0.9924 0.00 1.00
#> SRR2139981 1 0.141 0.9757 0.98 0.02
#> SRR2140000 2 0.000 0.9924 0.00 1.00
#> SRR2140077 2 0.000 0.9924 0.00 1.00
#> SRR2139986 2 0.000 0.9924 0.00 1.00
#> SRR2140070 2 0.000 0.9924 0.00 1.00
#> SRR2140007 2 0.000 0.9924 0.00 1.00
#> SRR2140048 2 0.000 0.9924 0.00 1.00
#> SRR2140035 2 0.000 0.9924 0.00 1.00
#> SRR2140042 2 0.000 0.9924 0.00 1.00
#> SRR2140063 2 0.000 0.9924 0.00 1.00
#> SRR2140014 2 0.000 0.9924 0.00 1.00
#> SRR2139995 2 0.000 0.9924 0.00 1.00
#> SRR2140069 2 0.000 0.9924 0.00 1.00
#> SRR2140026 2 0.000 0.9924 0.00 1.00
#> SRR2140051 2 0.000 0.9924 0.00 1.00
#> SRR2140061 2 0.000 0.9924 0.00 1.00
#> SRR2140016 2 0.000 0.9924 0.00 1.00
#> SRR2139979 2 0.000 0.9924 0.00 1.00
#> SRR2139997 2 0.000 0.9924 0.00 1.00
#> SRR2140085 2 0.000 0.9924 0.00 1.00
#> SRR2140024 2 0.000 0.9924 0.00 1.00
#> SRR2140053 2 0.000 0.9924 0.00 1.00
#> SRR2140059 2 0.000 0.9924 0.00 1.00
#> SRR2140078 2 0.000 0.9924 0.00 1.00
#> SRR2139984 2 0.000 0.9924 0.00 1.00
#> SRR2140072 1 1.000 -0.0068 0.50 0.50
#> SRR2140005 2 0.000 0.9924 0.00 1.00
#> SRR2140037 1 0.000 0.9945 1.00 0.00
#> SRR2140040 1 0.141 0.9757 0.98 0.02
#> SRR2140047 2 0.000 0.9924 0.00 1.00
#> SRR2140030 2 0.000 0.9924 0.00 1.00
#> SRR2140008 2 0.000 0.9924 0.00 1.00
#> SRR2139983 2 0.000 0.9924 0.00 1.00
#> SRR2139989 2 0.000 0.9924 0.00 1.00
#> SRR2140002 2 0.000 0.9924 0.00 1.00
#> SRR2140075 2 0.000 0.9924 0.00 1.00
#> SRR2140054 2 0.000 0.9924 0.00 1.00
#> SRR2140023 2 0.000 0.9924 0.00 1.00
#> SRR2140029 2 0.000 0.9924 0.00 1.00
#> SRR2140011 2 0.000 0.9924 0.00 1.00
#> SRR2140066 2 0.000 0.9924 0.00 1.00
#> SRR2139990 2 0.000 0.9924 0.00 1.00
#> SRR2140082 2 0.000 0.9924 0.00 1.00
#> SRR2140086 2 0.000 0.9924 0.00 1.00
#> SRR2140068 2 0.000 0.9924 0.00 1.00
#> SRR2139994 2 0.000 0.9924 0.00 1.00
#> SRR2140015 2 0.000 0.9924 0.00 1.00
#> SRR2140062 2 0.000 0.9924 0.00 1.00
#> SRR2140050 2 0.000 0.9924 0.00 1.00
#> SRR2140027 1 0.242 0.9557 0.96 0.04
#> SRR2140006 2 0.000 0.9924 0.00 1.00
#> SRR2140071 2 0.722 0.7541 0.20 0.80
#> SRR2139987 2 0.000 0.9924 0.00 1.00
#> SRR2140043 2 0.000 0.9924 0.00 1.00
#> SRR2140034 2 0.000 0.9924 0.00 1.00
#> SRR2140049 2 0.000 0.9924 0.00 1.00
#> SRR2140033 2 0.000 0.9924 0.00 1.00
#> SRR2140044 2 0.000 0.9924 0.00 1.00
#> SRR2140039 2 0.000 0.9924 0.00 1.00
#> SRR2140076 2 0.000 0.9924 0.00 1.00
#> SRR2140001 2 0.000 0.9924 0.00 1.00
#> SRR2139980 2 0.000 0.9924 0.00 1.00
#> SRR2140020 2 0.000 0.9924 0.00 1.00
#> SRR2140057 2 0.000 0.9924 0.00 1.00
#> SRR2140018 2 0.000 0.9924 0.00 1.00
#> SRR2140081 2 0.000 0.9924 0.00 1.00
#> SRR2139993 2 0.000 0.9924 0.00 1.00
#> SRR2139999 2 0.000 0.9924 0.00 1.00
#> SRR2139977 2 0.000 0.9924 0.00 1.00
#> SRR2140065 2 0.000 0.9924 0.00 1.00
#> SRR2140012 2 0.000 0.9924 0.00 1.00
#> SRR2139847 2 0.000 0.9924 0.00 1.00
#> SRR2139830 1 0.000 0.9945 1.00 0.00
#> SRR2139787 1 0.000 0.9945 1.00 0.00
#> SRR2139769 1 0.000 0.9945 1.00 0.00
#> SRR2139680 1 0.000 0.9945 1.00 0.00
#> SRR2139714 1 0.000 0.9945 1.00 0.00
#> SRR2139763 1 0.000 0.9945 1.00 0.00
#> SRR2139808 1 0.000 0.9945 1.00 0.00
#> SRR2139802 2 0.000 0.9924 0.00 1.00
#> SRR2139751 2 0.000 0.9924 0.00 1.00
#> SRR2139726 1 0.000 0.9945 1.00 0.00
#> SRR2139854 2 0.000 0.9924 0.00 1.00
#> SRR2139823 1 0.000 0.9945 1.00 0.00
#> SRR2139829 1 0.141 0.9757 0.98 0.02
#> SRR2139693 1 0.000 0.9945 1.00 0.00
#> SRR2139707 1 0.000 0.9945 1.00 0.00
#> SRR2139770 2 0.000 0.9924 0.00 1.00
#> SRR2139699 1 0.000 0.9945 1.00 0.00
#> SRR2139677 1 0.000 0.9945 1.00 0.00
#> SRR2139794 1 0.000 0.9945 1.00 0.00
#> SRR2139811 1 0.000 0.9945 1.00 0.00
#> SRR2139742 1 0.000 0.9945 1.00 0.00
#> SRR2139735 2 0.795 0.6880 0.24 0.76
#> SRR2139748 1 0.000 0.9945 1.00 0.00
#> SRR2139732 1 0.000 0.9945 1.00 0.00
#> SRR2139745 1 0.000 0.9945 1.00 0.00
#> SRR2139738 1 0.000 0.9945 1.00 0.00
#> SRR2139816 1 0.000 0.9945 1.00 0.00
#> SRR2139799 1 0.000 0.9945 1.00 0.00
#> SRR2139777 1 0.000 0.9945 1.00 0.00
#> SRR2139700 1 0.000 0.9945 1.00 0.00
#> SRR2139694 1 0.000 0.9945 1.00 0.00
#> SRR2139793 1 0.000 0.9945 1.00 0.00
#> SRR2139670 1 0.000 0.9945 1.00 0.00
#> SRR2139824 1 0.000 0.9945 1.00 0.00
#> SRR2139853 2 0.000 0.9924 0.00 1.00
#> SRR2139721 2 0.000 0.9924 0.00 1.00
#> SRR2139756 2 0.000 0.9924 0.00 1.00
#> SRR2139805 1 0.000 0.9945 1.00 0.00
#> SRR2139719 1 0.000 0.9945 1.00 0.00
#> SRR2139780 1 0.000 0.9945 1.00 0.00
#> SRR2139764 1 0.000 0.9945 1.00 0.00
#> SRR2139713 1 0.000 0.9945 1.00 0.00
#> SRR2139687 2 0.000 0.9924 0.00 1.00
#> SRR2139669 2 0.000 0.9924 0.00 1.00
#> SRR2139837 1 0.000 0.9945 1.00 0.00
#> SRR2139840 1 0.000 0.9945 1.00 0.00
#> SRR2139760 1 0.000 0.9945 1.00 0.00
#> SRR2139683 1 0.000 0.9945 1.00 0.00
#> SRR2139717 1 0.000 0.9945 1.00 0.00
#> SRR2139784 1 0.584 0.8368 0.86 0.14
#> SRR2139689 1 0.000 0.9945 1.00 0.00
#> SRR2139833 1 0.000 0.9945 1.00 0.00
#> SRR2139844 2 0.000 0.9924 0.00 1.00
#> SRR2139839 1 0.000 0.9945 1.00 0.00
#> SRR2139725 1 0.000 0.9945 1.00 0.00
#> SRR2139752 1 0.000 0.9945 1.00 0.00
#> SRR2139758 1 0.000 0.9945 1.00 0.00
#> SRR2139801 2 0.000 0.9924 0.00 1.00
#> SRR2139779 1 0.000 0.9945 1.00 0.00
#> SRR2139797 1 0.000 0.9945 1.00 0.00
#> SRR2139674 1 0.000 0.9945 1.00 0.00
#> SRR2139773 1 0.000 0.9945 1.00 0.00
#> SRR2139690 2 0.242 0.9536 0.04 0.96
#> SRR2139704 2 0.000 0.9924 0.00 1.00
#> SRR2139820 1 0.000 0.9945 1.00 0.00
#> SRR2139857 1 0.000 0.9945 1.00 0.00
#> SRR2139736 1 0.000 0.9945 1.00 0.00
#> SRR2139741 1 0.000 0.9945 1.00 0.00
#> SRR2139818 1 0.000 0.9945 1.00 0.00
#> SRR2139812 2 0.000 0.9924 0.00 1.00
#> SRR2139815 1 0.000 0.9945 1.00 0.00
#> SRR2139746 2 0.000 0.9924 0.00 1.00
#> SRR2139731 1 0.000 0.9945 1.00 0.00
#> SRR2139850 2 0.000 0.9924 0.00 1.00
#> SRR2139827 1 0.000 0.9945 1.00 0.00
#> SRR2139673 1 0.000 0.9945 1.00 0.00
#> SRR2139790 1 0.000 0.9945 1.00 0.00
#> SRR2139709 2 0.000 0.9924 0.00 1.00
#> SRR2139679 1 0.000 0.9945 1.00 0.00
#> SRR2139703 2 0.000 0.9924 0.00 1.00
#> SRR2139697 2 0.000 0.9924 0.00 1.00
#> SRR2139774 1 0.000 0.9945 1.00 0.00
#> SRR2139806 1 0.000 0.9945 1.00 0.00
#> SRR2139755 1 0.000 0.9945 1.00 0.00
#> SRR2139722 1 0.000 0.9945 1.00 0.00
#> SRR2139728 1 0.000 0.9945 1.00 0.00
#> SRR2139843 2 0.000 0.9924 0.00 1.00
#> SRR2139834 1 0.000 0.9945 1.00 0.00
#> SRR2139849 2 0.000 0.9924 0.00 1.00
#> SRR2139710 1 0.000 0.9945 1.00 0.00
#> SRR2139684 2 0.000 0.9924 0.00 1.00
#> SRR2139767 2 0.000 0.9924 0.00 1.00
#> SRR2139789 2 0.722 0.7543 0.20 0.80
#> SRR2139783 2 0.000 0.9924 0.00 1.00
#> SRR2139757 1 0.000 0.9945 1.00 0.00
#> SRR2139720 1 0.000 0.9945 1.00 0.00
#> SRR2139804 1 0.000 0.9945 1.00 0.00
#> SRR2139712 1 0.000 0.9945 1.00 0.00
#> SRR2139686 2 0.722 0.7537 0.20 0.80
#> SRR2139765 1 0.000 0.9945 1.00 0.00
#> SRR2139718 1 0.000 0.9945 1.00 0.00
#> SRR2139781 1 0.000 0.9945 1.00 0.00
#> SRR2139841 1 0.000 0.9945 1.00 0.00
#> SRR2139836 1 0.000 0.9945 1.00 0.00
#> SRR2139739 1 0.000 0.9945 1.00 0.00
#> SRR2139744 1 0.000 0.9945 1.00 0.00
#> SRR2139733 1 0.000 0.9945 1.00 0.00
#> SRR2139817 1 0.000 0.9945 1.00 0.00
#> SRR2139671 1 0.000 0.9945 1.00 0.00
#> SRR2139792 1 0.000 0.9945 1.00 0.00
#> SRR2139798 1 0.000 0.9945 1.00 0.00
#> SRR2139701 1 0.000 0.9945 1.00 0.00
#> SRR2139695 1 0.000 0.9945 1.00 0.00
#> SRR2139776 1 0.000 0.9945 1.00 0.00
#> SRR2139858 1 0.000 0.9945 1.00 0.00
#> SRR2139852 2 0.000 0.9924 0.00 1.00
#> SRR2139825 1 0.000 0.9945 1.00 0.00
#> SRR2139828 1 0.000 0.9945 1.00 0.00
#> SRR2139822 1 0.000 0.9945 1.00 0.00
#> SRR2139855 2 0.000 0.9924 0.00 1.00
#> SRR2139698 2 0.000 0.9924 0.00 1.00
#> SRR2139795 1 0.000 0.9945 1.00 0.00
#> SRR2139676 1 0.000 0.9945 1.00 0.00
#> SRR2139771 1 0.000 0.9945 1.00 0.00
#> SRR2139692 2 0.000 0.9924 0.00 1.00
#> SRR2139706 1 0.000 0.9945 1.00 0.00
#> SRR2139810 1 0.000 0.9945 1.00 0.00
#> SRR2139749 1 0.000 0.9945 1.00 0.00
#> SRR2139734 2 0.000 0.9924 0.00 1.00
#> SRR2139743 1 0.000 0.9945 1.00 0.00
#> SRR2139831 1 0.000 0.9945 1.00 0.00
#> SRR2139846 2 0.000 0.9924 0.00 1.00
#> SRR2139762 1 0.000 0.9945 1.00 0.00
#> SRR2139681 1 0.242 0.9558 0.96 0.04
#> SRR2139715 1 0.000 0.9945 1.00 0.00
#> SRR2139786 1 0.000 0.9945 1.00 0.00
#> SRR2139768 1 0.000 0.9945 1.00 0.00
#> SRR2139803 1 0.000 0.9945 1.00 0.00
#> SRR2139809 1 0.000 0.9945 1.00 0.00
#> SRR2139727 1 0.000 0.9945 1.00 0.00
#> SRR2139750 1 0.000 0.9945 1.00 0.00
#> SRR2139807 2 0.000 0.9924 0.00 1.00
#> SRR2139729 2 0.000 0.9924 0.00 1.00
#> SRR2139723 1 0.000 0.9945 1.00 0.00
#> SRR2139754 1 0.242 0.9556 0.96 0.04
#> SRR2139848 1 0.141 0.9757 0.98 0.02
#> SRR2139835 1 0.000 0.9945 1.00 0.00
#> SRR2139842 2 0.000 0.9924 0.00 1.00
#> SRR2139782 1 0.000 0.9945 1.00 0.00
#> SRR2139766 1 0.000 0.9945 1.00 0.00
#> SRR2139711 1 0.000 0.9945 1.00 0.00
#> SRR2139685 1 0.000 0.9945 1.00 0.00
#> SRR2139788 1 0.000 0.9945 1.00 0.00
#> SRR2139814 1 0.000 0.9945 1.00 0.00
#> SRR2139730 1 0.000 0.9945 1.00 0.00
#> SRR2139747 1 0.000 0.9945 1.00 0.00
#> SRR2139826 2 0.000 0.9924 0.00 1.00
#> SRR2139851 2 0.000 0.9924 0.00 1.00
#> SRR2139678 1 0.000 0.9945 1.00 0.00
#> SRR2139775 1 0.000 0.9945 1.00 0.00
#> SRR2139702 2 0.000 0.9924 0.00 1.00
#> SRR2139696 2 0.000 0.9924 0.00 1.00
#> SRR2139791 2 0.760 0.7236 0.22 0.78
#> SRR2139672 1 0.000 0.9945 1.00 0.00
#> SRR2139708 1 0.000 0.9945 1.00 0.00
#> SRR2139691 1 0.000 0.9945 1.00 0.00
#> SRR2139705 2 0.141 0.9736 0.02 0.98
#> SRR2139772 1 0.000 0.9945 1.00 0.00
#> SRR2139778 1 0.000 0.9945 1.00 0.00
#> SRR2139675 1 0.000 0.9945 1.00 0.00
#> SRR2139796 1 0.000 0.9945 1.00 0.00
#> SRR2139856 1 0.000 0.9945 1.00 0.00
#> SRR2139821 1 0.000 0.9945 1.00 0.00
#> SRR2139740 1 0.000 0.9945 1.00 0.00
#> SRR2139737 1 0.402 0.9116 0.92 0.08
#> SRR2139813 2 0.000 0.9924 0.00 1.00
#> SRR2139819 1 0.000 0.9945 1.00 0.00
#> SRR2139785 1 0.000 0.9945 1.00 0.00
#> SRR2139688 1 0.000 0.9945 1.00 0.00
#> SRR2139682 2 0.000 0.9924 0.00 1.00
#> SRR2139716 1 0.000 0.9945 1.00 0.00
#> SRR2139761 1 0.000 0.9945 1.00 0.00
#> SRR2139838 1 0.000 0.9945 1.00 0.00
#> SRR2139845 2 0.000 0.9924 0.00 1.00
#> SRR2139832 1 0.529 0.8637 0.88 0.12
#> SRR2139759 1 0.000 0.9945 1.00 0.00
#> SRR2139753 1 0.000 0.9945 1.00 0.00
#> SRR2139724 1 0.000 0.9945 1.00 0.00
#> SRR2139800 1 0.000 0.9945 1.00 0.00
#> SRR2139306 1 0.000 0.9945 1.00 0.00
#> SRR2139371 1 0.000 0.9945 1.00 0.00
#> SRR2139343 1 0.000 0.9945 1.00 0.00
#> SRR2139334 1 0.000 0.9945 1.00 0.00
#> SRR2139349 1 0.000 0.9945 1.00 0.00
#> SRR2139368 1 0.000 0.9945 1.00 0.00
#> SRR2139315 1 0.000 0.9945 1.00 0.00
#> SRR2139362 1 0.000 0.9945 1.00 0.00
#> SRR2139350 1 0.000 0.9945 1.00 0.00
#> SRR2139327 1 0.000 0.9945 1.00 0.00
#> SRR2139320 1 0.000 0.9945 1.00 0.00
#> SRR2139357 1 0.000 0.9945 1.00 0.00
#> SRR2139318 1 0.000 0.9945 1.00 0.00
#> SRR2139381 1 0.000 0.9945 1.00 0.00
#> SRR2139365 1 0.000 0.9945 1.00 0.00
#> SRR2139312 1 0.000 0.9945 1.00 0.00
#> SRR2139333 2 0.000 0.9924 0.00 1.00
#> SRR2139344 1 0.000 0.9945 1.00 0.00
#> SRR2139339 1 0.000 0.9945 1.00 0.00
#> SRR2139376 1 0.000 0.9945 1.00 0.00
#> SRR2139378 1 0.000 0.9945 1.00 0.00
#> SRR2139372 1 0.000 0.9945 1.00 0.00
#> SRR2139337 1 0.000 0.9945 1.00 0.00
#> SRR2139340 1 0.000 0.9945 1.00 0.00
#> SRR2139361 1 0.000 0.9945 1.00 0.00
#> SRR2139316 1 0.000 0.9945 1.00 0.00
#> SRR2139324 1 0.000 0.9945 1.00 0.00
#> SRR2139353 1 0.000 0.9945 1.00 0.00
#> SRR2139359 1 0.000 0.9945 1.00 0.00
#> SRR2139354 1 0.000 0.9945 1.00 0.00
#> SRR2139323 1 0.000 0.9945 1.00 0.00
#> SRR2139329 1 0.000 0.9945 1.00 0.00
#> SRR2139311 1 0.000 0.9945 1.00 0.00
#> SRR2139366 1 0.000 0.9945 1.00 0.00
#> SRR2139382 1 0.000 0.9945 1.00 0.00
#> SRR2139347 1 0.000 0.9945 1.00 0.00
#> SRR2139330 1 0.000 0.9945 1.00 0.00
#> SRR2139308 1 0.000 0.9945 1.00 0.00
#> SRR2139375 1 0.000 0.9945 1.00 0.00
#> SRR2139338 1 0.000 0.9945 1.00 0.00
#> SRR2139345 1 0.000 0.9945 1.00 0.00
#> SRR2139332 1 0.000 0.9945 1.00 0.00
#> SRR2139377 1 0.000 0.9945 1.00 0.00
#> SRR2139356 1 0.000 0.9945 1.00 0.00
#> SRR2139321 1 0.000 0.9945 1.00 0.00
#> SRR2139313 1 0.000 0.9945 1.00 0.00
#> SRR2139364 1 0.000 0.9945 1.00 0.00
#> SRR2139319 1 0.000 0.9945 1.00 0.00
#> SRR2139380 1 0.000 0.9945 1.00 0.00
#> SRR2139363 1 0.000 0.9945 1.00 0.00
#> SRR2139314 1 0.000 0.9945 1.00 0.00
#> SRR2139369 1 0.000 0.9945 1.00 0.00
#> SRR2139326 1 0.000 0.9945 1.00 0.00
#> SRR2139351 1 0.000 0.9945 1.00 0.00
#> SRR2139370 1 0.000 0.9945 1.00 0.00
#> SRR2139307 1 0.000 0.9945 1.00 0.00
#> SRR2139348 1 0.000 0.9945 1.00 0.00
#> SRR2139335 1 0.000 0.9945 1.00 0.00
#> SRR2139342 1 0.000 0.9945 1.00 0.00
#> SRR2139331 1 0.000 0.9945 1.00 0.00
#> SRR2139346 1 0.000 0.9945 1.00 0.00
#> SRR2139374 1 0.000 0.9945 1.00 0.00
#> SRR2139309 1 0.000 0.9945 1.00 0.00
#> SRR2139328 1 0.000 0.9945 1.00 0.00
#> SRR2139322 1 0.000 0.9945 1.00 0.00
#> SRR2139355 1 0.000 0.9945 1.00 0.00
#> SRR2139383 2 0.000 0.9924 0.00 1.00
#> SRR2139367 1 0.000 0.9945 1.00 0.00
#> SRR2139310 1 0.000 0.9945 1.00 0.00
#> SRR2139384 2 0.000 0.9924 0.00 1.00
#> SRR2139317 1 0.000 0.9945 1.00 0.00
#> SRR2139360 1 0.000 0.9945 1.00 0.00
#> SRR2139358 1 0.000 0.9945 1.00 0.00
#> SRR2139352 1 0.000 0.9945 1.00 0.00
#> SRR2139325 2 0.000 0.9924 0.00 1.00
#> SRR2139373 1 0.000 0.9945 1.00 0.00
#> SRR2139379 1 0.000 0.9945 1.00 0.00
#> SRR2139341 1 0.000 0.9945 1.00 0.00
#> SRR2139336 1 0.000 0.9945 1.00 0.00
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> SRR2140028 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140022 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140055 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140083 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139991 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140067 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140010 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140031 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140046 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140074 2 0.4555 0.771 0.20 0.80 0.00
#> SRR2140003 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139988 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139982 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140009 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140004 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2140073 2 0.2537 0.886 0.08 0.92 0.00
#> SRR2139985 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140079 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140041 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140036 2 0.9444 0.173 0.38 0.44 0.18
#> SRR2140084 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139978 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139996 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140017 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140060 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140058 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140052 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140025 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140056 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140021 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140013 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140064 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139998 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139992 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140019 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140080 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140038 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2140045 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140032 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139981 1 0.0000 0.642 1.00 0.00 0.00
#> SRR2140000 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140077 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139986 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140070 2 0.3686 0.832 0.14 0.86 0.00
#> SRR2140007 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140048 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140035 2 0.5948 0.571 0.36 0.64 0.00
#> SRR2140042 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140063 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140014 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139995 1 0.4555 0.538 0.80 0.20 0.00
#> SRR2140069 2 0.6045 0.538 0.38 0.62 0.00
#> SRR2140026 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140051 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140061 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140016 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139979 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139997 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140085 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140024 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140053 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140059 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2140078 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139984 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140072 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2140005 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140037 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2140040 1 0.0892 0.646 0.98 0.00 0.02
#> SRR2140047 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140030 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140008 2 0.5948 0.571 0.36 0.64 0.00
#> SRR2139983 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139989 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140002 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140075 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140054 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140023 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140029 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140011 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140066 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139990 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140082 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140086 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140068 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139994 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140015 2 0.5948 0.571 0.36 0.64 0.00
#> SRR2140062 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140050 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140027 1 0.0892 0.646 0.98 0.00 0.02
#> SRR2140006 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140071 1 0.0000 0.642 1.00 0.00 0.00
#> SRR2139987 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140043 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140034 2 0.4002 0.812 0.16 0.84 0.00
#> SRR2140049 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140033 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140044 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140039 2 0.5948 0.571 0.36 0.64 0.00
#> SRR2140076 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140001 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139980 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140020 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140057 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140018 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140081 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139993 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139999 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139977 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140065 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2140012 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139847 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139830 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139787 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139769 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139680 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139714 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139763 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139808 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139802 2 0.0892 0.934 0.02 0.98 0.00
#> SRR2139751 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139726 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139854 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139823 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139829 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139693 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139707 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139770 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139699 1 0.6244 0.460 0.56 0.00 0.44
#> SRR2139677 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139794 1 0.6302 0.484 0.52 0.00 0.48
#> SRR2139811 1 0.2537 0.654 0.92 0.00 0.08
#> SRR2139742 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139735 1 0.4821 0.640 0.84 0.04 0.12
#> SRR2139748 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139732 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139745 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139738 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139816 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139799 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139777 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139700 1 0.6302 0.479 0.52 0.00 0.48
#> SRR2139694 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139793 1 0.1529 0.650 0.96 0.00 0.04
#> SRR2139670 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139824 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139853 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139721 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139756 2 0.5948 0.571 0.36 0.64 0.00
#> SRR2139805 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139719 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139780 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139764 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139713 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139687 2 0.6045 0.538 0.38 0.62 0.00
#> SRR2139669 2 0.0892 0.935 0.02 0.98 0.00
#> SRR2139837 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139840 3 0.5948 0.329 0.36 0.00 0.64
#> SRR2139760 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139683 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139717 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139784 1 0.5147 0.631 0.80 0.02 0.18
#> SRR2139689 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139833 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139844 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139839 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139725 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139752 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139758 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139801 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139779 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139797 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139674 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139773 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139690 3 0.6280 0.105 0.00 0.46 0.54
#> SRR2139704 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139820 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139857 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139736 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139741 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139818 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139812 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139815 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139746 2 0.4291 0.791 0.18 0.82 0.00
#> SRR2139731 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139850 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139827 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139673 1 0.5016 0.580 0.76 0.00 0.24
#> SRR2139790 1 0.2537 0.654 0.92 0.00 0.08
#> SRR2139709 2 0.8538 0.357 0.38 0.52 0.10
#> SRR2139679 1 0.2537 0.654 0.92 0.00 0.08
#> SRR2139703 2 0.6244 0.416 0.44 0.56 0.00
#> SRR2139697 2 0.5948 0.571 0.36 0.64 0.00
#> SRR2139774 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139806 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139755 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139722 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139728 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139843 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139834 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139849 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139710 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139684 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139767 3 0.7424 0.375 0.30 0.06 0.64
#> SRR2139789 3 0.5560 0.507 0.00 0.30 0.70
#> SRR2139783 2 0.6758 0.542 0.36 0.62 0.02
#> SRR2139757 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139720 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139804 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139712 3 0.1529 0.895 0.04 0.00 0.96
#> SRR2139686 1 0.5159 0.635 0.82 0.04 0.14
#> SRR2139765 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139718 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139781 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139841 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139836 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139739 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139744 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139733 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139817 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139671 3 0.5948 0.329 0.36 0.00 0.64
#> SRR2139792 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139798 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139701 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139695 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139776 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139858 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139852 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139825 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139828 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139822 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139855 2 0.1529 0.916 0.04 0.96 0.00
#> SRR2139698 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139795 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139676 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139771 3 0.6244 0.161 0.44 0.00 0.56
#> SRR2139692 2 0.7464 0.431 0.40 0.56 0.04
#> SRR2139706 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139810 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139749 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139734 2 0.8635 0.199 0.44 0.46 0.10
#> SRR2139743 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139831 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139846 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139762 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139681 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139715 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139786 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139768 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139803 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139809 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139727 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139750 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139807 1 0.3832 0.614 0.88 0.10 0.02
#> SRR2139729 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139723 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139754 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139848 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139835 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139842 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139782 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139766 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139711 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139685 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139788 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139814 1 0.2066 0.652 0.94 0.00 0.06
#> SRR2139730 1 0.5397 0.523 0.72 0.00 0.28
#> SRR2139747 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139826 1 0.3340 0.601 0.88 0.12 0.00
#> SRR2139851 2 0.0892 0.934 0.02 0.98 0.00
#> SRR2139678 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139775 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139702 1 0.4291 0.557 0.82 0.18 0.00
#> SRR2139696 1 0.3686 0.589 0.86 0.14 0.00
#> SRR2139791 3 0.5397 0.530 0.00 0.28 0.72
#> SRR2139672 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139708 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139691 1 0.4555 0.628 0.80 0.00 0.20
#> SRR2139705 1 0.2959 0.612 0.90 0.10 0.00
#> SRR2139772 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139778 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139675 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139796 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139856 1 0.6045 0.579 0.62 0.00 0.38
#> SRR2139821 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139740 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139737 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139813 2 0.1529 0.920 0.04 0.96 0.00
#> SRR2139819 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139785 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139688 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139682 2 0.5948 0.571 0.36 0.64 0.00
#> SRR2139716 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139761 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139838 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139845 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139832 1 0.0892 0.646 0.98 0.00 0.02
#> SRR2139759 1 0.5948 0.611 0.64 0.00 0.36
#> SRR2139753 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139724 1 0.4291 0.648 0.82 0.00 0.18
#> SRR2139800 1 0.2066 0.652 0.94 0.00 0.06
#> SRR2139306 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139371 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139343 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139334 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139349 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139368 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139315 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139362 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139350 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139327 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139320 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139357 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139318 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139381 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139365 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139312 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139333 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139344 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139339 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139376 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139378 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139372 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139337 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139340 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139361 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139316 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139324 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139353 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139359 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139354 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139323 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139329 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139311 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139366 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139382 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139347 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139330 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139308 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139375 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139338 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139345 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139332 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139377 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139356 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139321 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139313 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139364 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139319 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139380 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139363 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139314 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139369 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139326 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139351 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139370 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139307 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139348 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139335 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139342 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139331 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139346 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139374 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139309 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139328 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139322 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139355 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139383 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139367 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139310 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139384 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139317 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139360 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139358 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139352 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139325 2 0.0000 0.950 0.00 1.00 0.00
#> SRR2139373 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139379 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139341 3 0.0000 0.954 0.00 0.00 1.00
#> SRR2139336 3 0.0000 0.954 0.00 0.00 1.00
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> SRR2140028 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140022 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140055 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140083 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139991 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140067 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140010 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140031 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140046 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140074 2 0.4522 0.543 0.32 0.68 0.00 0.00
#> SRR2140003 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139988 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139982 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140009 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140004 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2140073 2 0.1211 0.944 0.04 0.96 0.00 0.00
#> SRR2139985 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140079 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140041 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140036 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2140084 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139978 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139996 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140017 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140060 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140058 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140052 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140025 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140056 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140021 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140013 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140064 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139998 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139992 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140019 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140080 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140038 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2140045 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140032 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139981 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2140000 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140077 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139986 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140070 2 0.4406 0.583 0.30 0.70 0.00 0.00
#> SRR2140007 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140048 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140035 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2140042 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140063 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140014 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139995 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2140069 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2140026 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140051 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140061 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140016 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139979 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139997 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140085 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140024 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140053 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140059 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2140078 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139984 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140072 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2140005 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140037 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2140040 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2140047 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140030 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140008 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139983 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139989 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140002 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140075 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140054 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140023 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140029 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140011 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140066 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139990 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140082 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140086 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140068 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139994 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140015 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2140062 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140050 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140027 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2140006 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140071 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139987 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140043 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140034 2 0.3172 0.810 0.16 0.84 0.00 0.00
#> SRR2140049 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140033 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140044 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140039 1 0.1637 0.930 0.94 0.06 0.00 0.00
#> SRR2140076 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140001 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139980 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140020 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140057 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140018 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140081 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139993 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139999 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139977 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140065 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2140012 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139847 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139830 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139787 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139769 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139680 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139714 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139763 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139808 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139802 2 0.4277 0.618 0.00 0.72 0.00 0.28
#> SRR2139751 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139726 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139854 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139823 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139829 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139693 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139707 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139770 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139699 4 0.0707 0.977 0.00 0.00 0.02 0.98
#> SRR2139677 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139794 4 0.0707 0.977 0.00 0.00 0.02 0.98
#> SRR2139811 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139742 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139735 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139748 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139732 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139745 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139738 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139816 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139799 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139777 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139700 4 0.5077 0.741 0.08 0.00 0.16 0.76
#> SRR2139694 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139793 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139670 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139824 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139853 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139721 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139756 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139805 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139719 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139780 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139764 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139713 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139687 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139669 2 0.2647 0.861 0.12 0.88 0.00 0.00
#> SRR2139837 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139840 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139760 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139683 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139717 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139784 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139689 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139833 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139844 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139839 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139725 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139752 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139758 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139801 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139779 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139797 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139674 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139773 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139690 3 0.2647 0.851 0.00 0.12 0.88 0.00
#> SRR2139704 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139820 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139857 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139736 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139741 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139818 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139812 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139815 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139746 2 0.4790 0.399 0.38 0.62 0.00 0.00
#> SRR2139731 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139850 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139827 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139673 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139790 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139709 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139679 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139703 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139697 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139774 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139806 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139755 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139722 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139728 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139843 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139834 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139849 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139710 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139684 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139767 3 0.4977 0.148 0.46 0.00 0.54 0.00
#> SRR2139789 3 0.1211 0.948 0.00 0.04 0.96 0.00
#> SRR2139783 1 0.1211 0.954 0.96 0.04 0.00 0.00
#> SRR2139757 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139720 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139804 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139712 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139686 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139765 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139718 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139781 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139841 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139836 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139739 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139744 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139733 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139817 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139671 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139792 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139798 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139701 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139695 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139776 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139858 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139852 2 0.2345 0.881 0.00 0.90 0.00 0.10
#> SRR2139825 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139828 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139822 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139855 2 0.3975 0.689 0.00 0.76 0.00 0.24
#> SRR2139698 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139795 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139676 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139771 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139692 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139706 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139810 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139749 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139734 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139743 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139831 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139846 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139762 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139681 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139715 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139786 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139768 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139803 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139809 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139727 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139750 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139807 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139729 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139723 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139754 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139848 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139835 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139842 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139782 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139766 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139711 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139685 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139788 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139814 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139730 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139747 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139826 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139851 2 0.3172 0.807 0.00 0.84 0.00 0.16
#> SRR2139678 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139775 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139702 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139696 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139791 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139672 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139708 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139691 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139705 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139772 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139778 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139675 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139796 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139856 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139821 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139740 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139737 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139813 2 0.1637 0.925 0.06 0.94 0.00 0.00
#> SRR2139819 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139785 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139688 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139682 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139716 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139761 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139838 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139845 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139832 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139759 4 0.0000 0.997 0.00 0.00 0.00 1.00
#> SRR2139753 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139724 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139800 1 0.0000 0.999 1.00 0.00 0.00 0.00
#> SRR2139306 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139371 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139343 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139334 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139349 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139368 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139315 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139362 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139350 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139327 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139320 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139357 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139318 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139381 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139365 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139312 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139333 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139344 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139339 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139376 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139378 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139372 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139337 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139340 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139361 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139316 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139324 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139353 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139359 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139354 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139323 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139329 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139311 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139366 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139382 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139347 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139330 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139308 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139375 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139338 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139345 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139332 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139377 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139356 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139321 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139313 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139364 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139319 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139380 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139363 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139314 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139369 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139326 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139351 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139370 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139307 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139348 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139335 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139342 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139331 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139346 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139374 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139309 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139328 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139322 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139355 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139383 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139367 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139310 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139384 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139317 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139360 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139358 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139352 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139325 2 0.0000 0.982 0.00 1.00 0.00 0.00
#> SRR2139373 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139379 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139341 3 0.0000 0.992 0.00 0.00 1.00 0.00
#> SRR2139336 3 0.0000 0.992 0.00 0.00 1.00 0.00
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
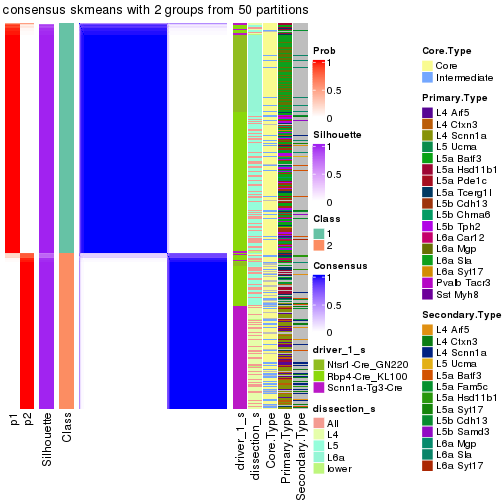
consensus_heatmap(res, k = 3)
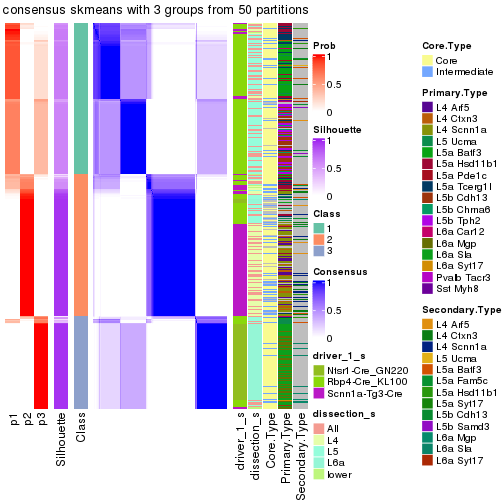
consensus_heatmap(res, k = 4)
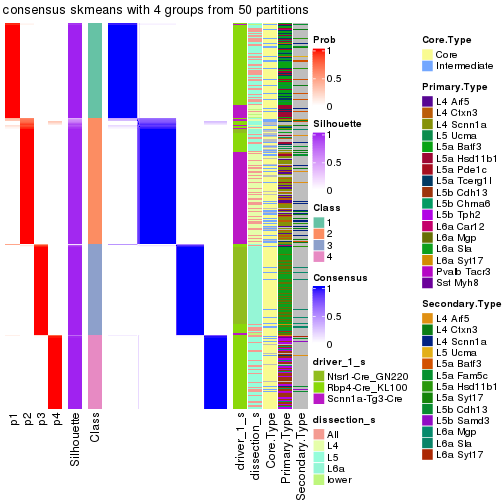
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
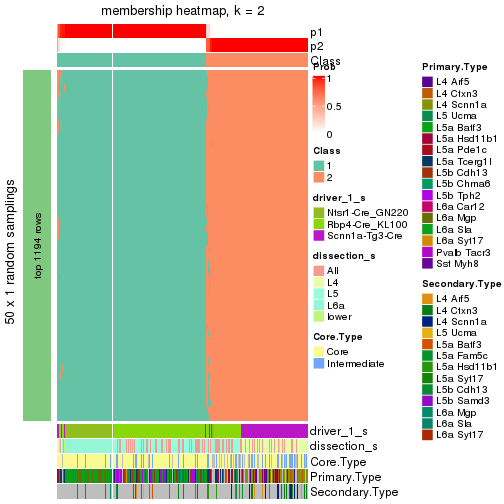
membership_heatmap(res, k = 3)
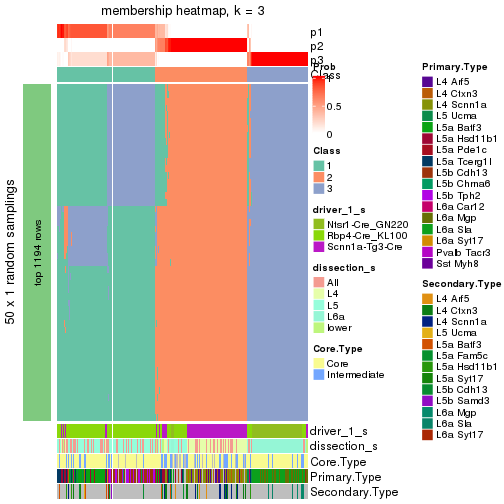
membership_heatmap(res, k = 4)
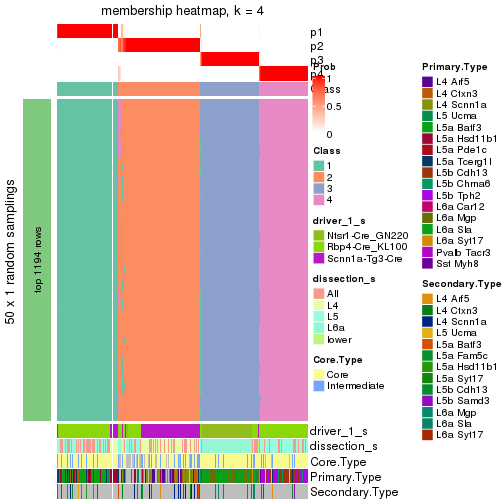
As soon as the classes for columns are determined, the signatures that are significantly different between subgroups can be looked for. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
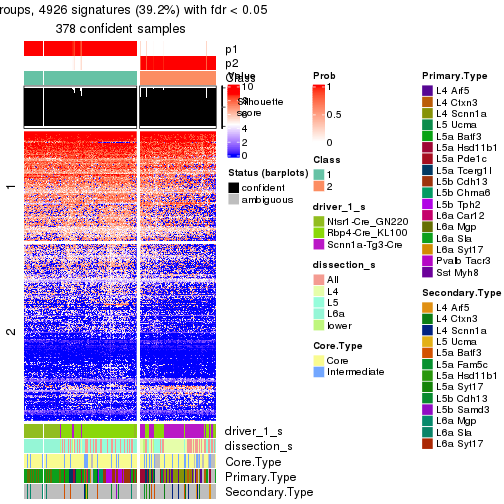
get_signatures(res, k = 3, scale_rows = FALSE)
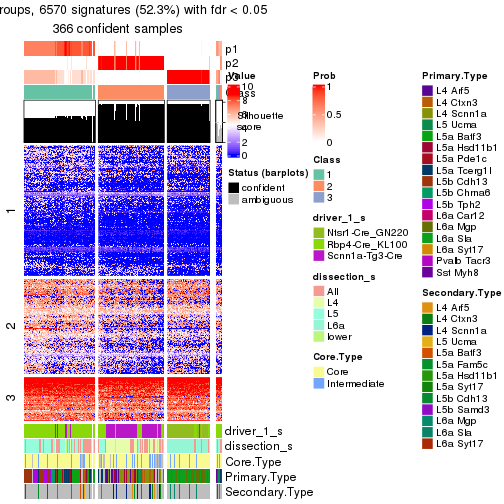
get_signatures(res, k = 4, scale_rows = FALSE)
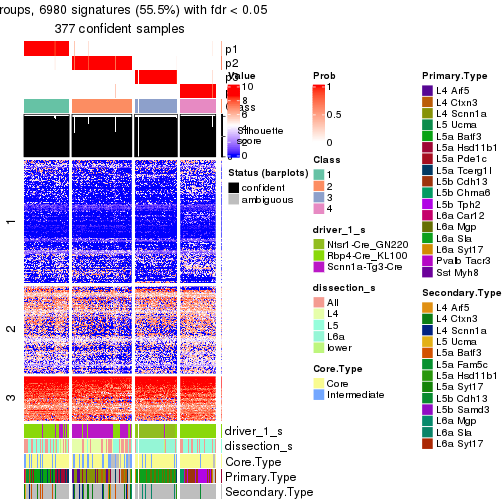
Compare the overlap of signatures from different k:
compare_signatures(res)
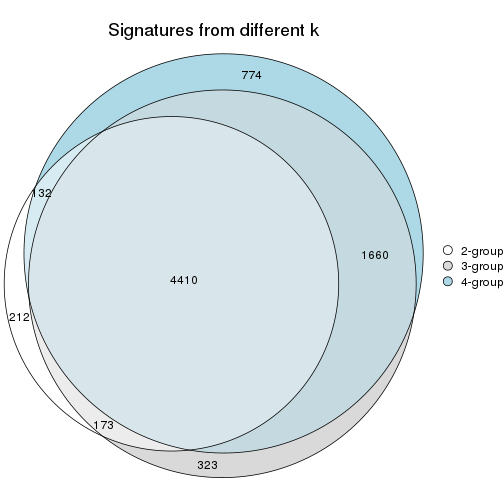
get_signature() returns a data frame invisibly. To get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows (which is done by automatically selecting number of clusters).If there are too many signatures, top_signatures = ... can be set to only show the
signatures with the highest FDRs:
# code only for demonstration
# e.g. to show the top 500 most significant rows
tb = get_signature(res, k = ..., top_signatures = 500)
If the signatures are defined as these which are uniquely high in current group, diff_method argument
can be set to "uniquely_high_in_one_group":
# code only for demonstration
tb = get_signature(res, k = ..., diff_method = "uniquely_high_in_one_group")
UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
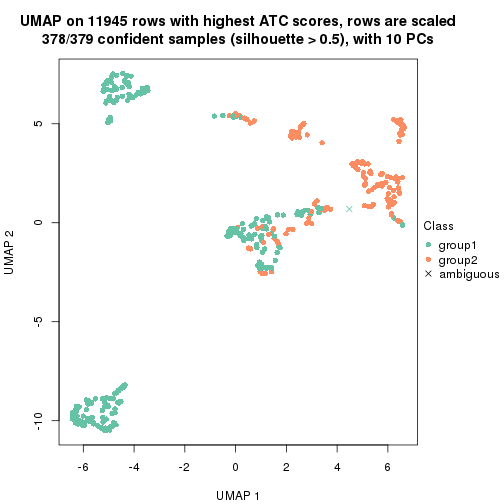
dimension_reduction(res, k = 3, method = "UMAP")
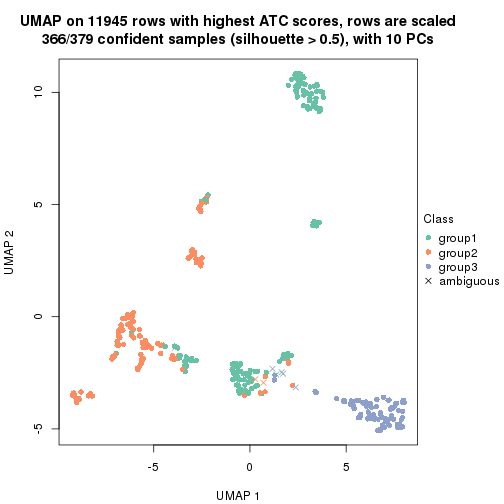
dimension_reduction(res, k = 4, method = "UMAP")
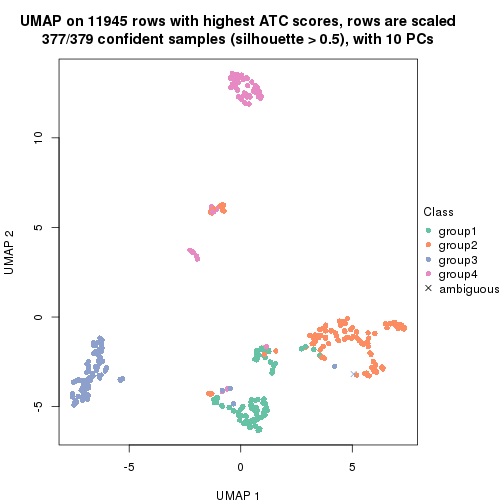
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
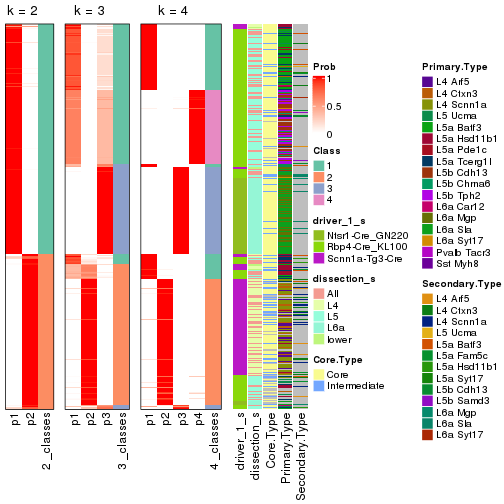
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n_sample driver_1_s(p-value) dissection_s(p-value) Core.Type(p-value)
#> ATC:skmeans 378 7.46e-43 9.06e-32 1.35e-05
#> ATC:skmeans 366 3.04e-99 5.18e-83 3.03e-05
#> ATC:skmeans 377 1.15e-99 2.57e-85 1.13e-04
#> Primary.Type(p-value) Secondary.Type(p-value) k
#> ATC:skmeans 2.09e-44 2.81e-07 2
#> ATC:skmeans 2.18e-98 2.10e-08 3
#> ATC:skmeans 2.21e-155 4.34e-10 4
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
Parent node: Node0. Child nodes: Node011-leaf , Node012-leaf , Node013-leaf , Node021 , Node022 , Node031-leaf , Node032-leaf , Node041-leaf , Node042-leaf .
The object with results only for a single top-value method and a single partitioning method can be extracted as:
res = res_rh["01"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4.
#> On a matrix with 11940 rows and 93 columns.
#> Top rows (989) are extracted by 'ATC' method.
#> Subgroups are detected by 'skmeans' method.
#> Performed in total 150 partitions by row resampling.
#> Best k for subgroups seems to be 3.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_partitions"
#> [7] "compare_signatures" "consensus_heatmap" "dimension_reduction"
#> [10] "functional_enrichment" "get_anno_col" "get_anno"
#> [13] "get_classes" "get_consensus" "get_matrix"
#> [16] "get_membership" "get_param" "get_signatures"
#> [19] "get_stats" "is_best_k" "is_stable_k"
#> [22] "membership_heatmap" "ncol" "nrow"
#> [25] "plot_ecdf" "predict_classes" "rownames"
#> [28] "select_partition_number" "show" "suggest_best_k"
#> [31] "test_to_known_factors" "top_rows_heatmap"
collect_plots() function collects all the plots made from res for all k (number of subgroups)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
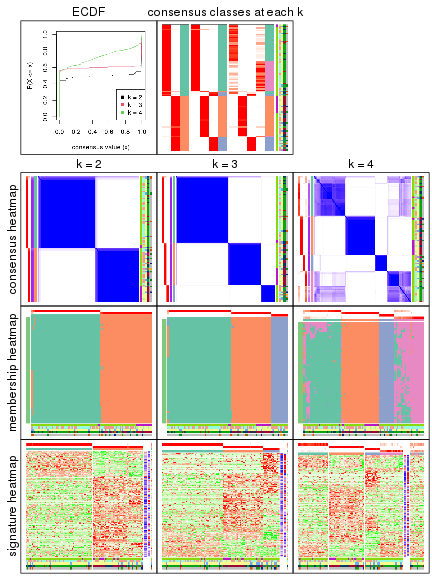
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, higher 1-PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
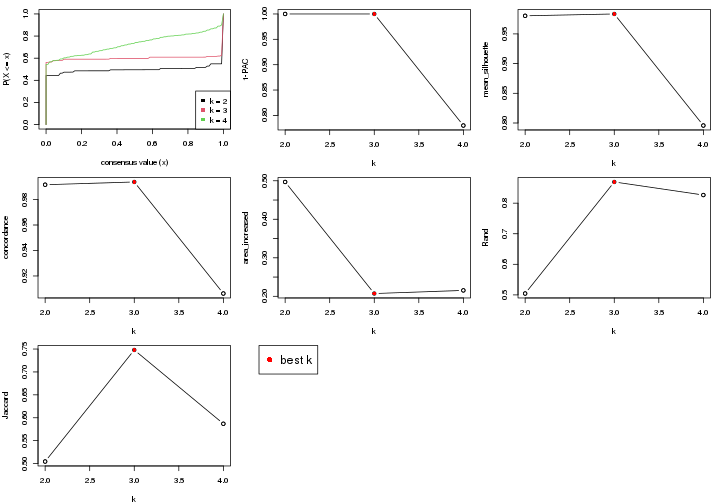
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 1.00 0.980 0.992 0.497 0.504 0.504
#> 3 3 1.00 0.984 0.994 0.207 0.869 0.748
#> 4 4 0.78 0.796 0.906 0.215 0.827 0.587
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 3
#> attr(,"optional")
#> [1] 2
There is also optional best \(k\) = 2 that is worth to check.
Following is the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall subgroup
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> SRR2140004 2 0.000 0.994 0.00 1.00
#> SRR2140036 1 0.000 0.989 1.00 0.00
#> SRR2139981 2 0.000 0.994 0.00 1.00
#> SRR2140035 2 0.000 0.994 0.00 1.00
#> SRR2139995 2 0.000 0.994 0.00 1.00
#> SRR2140069 2 0.000 0.994 0.00 1.00
#> SRR2140059 1 0.000 0.989 1.00 0.00
#> SRR2140072 2 0.000 0.994 0.00 1.00
#> SRR2140040 2 0.000 0.994 0.00 1.00
#> SRR2140008 2 0.000 0.994 0.00 1.00
#> SRR2140015 2 0.000 0.994 0.00 1.00
#> SRR2140027 2 0.000 0.994 0.00 1.00
#> SRR2140071 2 0.000 0.994 0.00 1.00
#> SRR2140039 2 0.000 0.994 0.00 1.00
#> SRR2139830 1 0.000 0.989 1.00 0.00
#> SRR2139726 1 0.000 0.989 1.00 0.00
#> SRR2139823 2 0.000 0.994 0.00 1.00
#> SRR2139693 1 0.000 0.989 1.00 0.00
#> SRR2139811 1 0.943 0.432 0.64 0.36
#> SRR2139735 1 0.402 0.908 0.92 0.08
#> SRR2139694 1 0.000 0.989 1.00 0.00
#> SRR2139793 2 0.000 0.994 0.00 1.00
#> SRR2139670 1 0.000 0.989 1.00 0.00
#> SRR2139824 1 0.000 0.989 1.00 0.00
#> SRR2139756 1 0.000 0.989 1.00 0.00
#> SRR2139805 1 0.000 0.989 1.00 0.00
#> SRR2139780 1 0.000 0.989 1.00 0.00
#> SRR2139764 1 0.000 0.989 1.00 0.00
#> SRR2139687 2 0.000 0.994 0.00 1.00
#> SRR2139840 2 0.000 0.994 0.00 1.00
#> SRR2139760 1 0.000 0.989 1.00 0.00
#> SRR2139784 1 0.000 0.989 1.00 0.00
#> SRR2139839 2 0.000 0.994 0.00 1.00
#> SRR2139779 1 0.000 0.989 1.00 0.00
#> SRR2139797 1 0.000 0.989 1.00 0.00
#> SRR2139674 1 0.000 0.989 1.00 0.00
#> SRR2139773 1 0.000 0.989 1.00 0.00
#> SRR2139818 1 0.000 0.989 1.00 0.00
#> SRR2139815 1 0.000 0.989 1.00 0.00
#> SRR2139731 1 0.000 0.989 1.00 0.00
#> SRR2139827 1 0.000 0.989 1.00 0.00
#> SRR2139673 1 0.000 0.989 1.00 0.00
#> SRR2139790 2 0.000 0.994 0.00 1.00
#> SRR2139709 1 0.000 0.989 1.00 0.00
#> SRR2139679 2 0.000 0.994 0.00 1.00
#> SRR2139703 2 0.000 0.994 0.00 1.00
#> SRR2139697 2 0.000 0.994 0.00 1.00
#> SRR2139834 1 0.000 0.989 1.00 0.00
#> SRR2139783 1 0.000 0.989 1.00 0.00
#> SRR2139804 2 0.000 0.994 0.00 1.00
#> SRR2139686 2 0.000 0.994 0.00 1.00
#> SRR2139765 1 0.000 0.989 1.00 0.00
#> SRR2139718 1 0.000 0.989 1.00 0.00
#> SRR2139841 1 0.000 0.989 1.00 0.00
#> SRR2139836 1 0.000 0.989 1.00 0.00
#> SRR2139739 1 0.000 0.989 1.00 0.00
#> SRR2139733 1 0.000 0.989 1.00 0.00
#> SRR2139671 1 0.469 0.886 0.90 0.10
#> SRR2139776 2 0.402 0.912 0.08 0.92
#> SRR2139822 1 0.000 0.989 1.00 0.00
#> SRR2139771 2 0.000 0.994 0.00 1.00
#> SRR2139692 1 0.000 0.989 1.00 0.00
#> SRR2139810 2 0.000 0.994 0.00 1.00
#> SRR2139734 1 0.000 0.989 1.00 0.00
#> SRR2139762 1 0.000 0.989 1.00 0.00
#> SRR2139681 1 0.000 0.989 1.00 0.00
#> SRR2139715 2 0.000 0.994 0.00 1.00
#> SRR2139803 1 0.000 0.989 1.00 0.00
#> SRR2139809 1 0.000 0.989 1.00 0.00
#> SRR2139807 2 0.000 0.994 0.00 1.00
#> SRR2139723 1 0.000 0.989 1.00 0.00
#> SRR2139754 1 0.000 0.989 1.00 0.00
#> SRR2139835 1 0.000 0.989 1.00 0.00
#> SRR2139814 2 0.000 0.994 0.00 1.00
#> SRR2139730 2 0.000 0.994 0.00 1.00
#> SRR2139747 2 0.634 0.809 0.16 0.84
#> SRR2139826 2 0.000 0.994 0.00 1.00
#> SRR2139678 2 0.000 0.994 0.00 1.00
#> SRR2139702 2 0.000 0.994 0.00 1.00
#> SRR2139696 2 0.000 0.994 0.00 1.00
#> SRR2139672 1 0.000 0.989 1.00 0.00
#> SRR2139691 2 0.000 0.994 0.00 1.00
#> SRR2139705 2 0.000 0.994 0.00 1.00
#> SRR2139772 1 0.000 0.989 1.00 0.00
#> SRR2139821 1 0.000 0.989 1.00 0.00
#> SRR2139737 1 0.000 0.989 1.00 0.00
#> SRR2139688 1 0.000 0.989 1.00 0.00
#> SRR2139682 1 0.000 0.989 1.00 0.00
#> SRR2139838 2 0.000 0.994 0.00 1.00
#> SRR2139832 2 0.000 0.994 0.00 1.00
#> SRR2139753 1 0.000 0.989 1.00 0.00
#> SRR2139724 1 0.000 0.989 1.00 0.00
#> SRR2139800 2 0.000 0.994 0.00 1.00
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> SRR2140004 2 0.0000 0.995 0.00 1.00 0.00
#> SRR2140036 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139981 2 0.0000 0.995 0.00 1.00 0.00
#> SRR2140035 2 0.0000 0.995 0.00 1.00 0.00
#> SRR2139995 2 0.0000 0.995 0.00 1.00 0.00
#> SRR2140069 2 0.0000 0.995 0.00 1.00 0.00
#> SRR2140059 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2140072 2 0.0000 0.995 0.00 1.00 0.00
#> SRR2140040 2 0.0000 0.995 0.00 1.00 0.00
#> SRR2140008 2 0.0000 0.995 0.00 1.00 0.00
#> SRR2140015 2 0.0000 0.995 0.00 1.00 0.00
#> SRR2140027 2 0.0000 0.995 0.00 1.00 0.00
#> SRR2140071 2 0.0000 0.995 0.00 1.00 0.00
#> SRR2140039 2 0.0000 0.995 0.00 1.00 0.00
#> SRR2139830 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139726 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139823 3 0.0000 0.996 0.00 0.00 1.00
#> SRR2139693 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139811 2 0.2959 0.857 0.10 0.90 0.00
#> SRR2139735 1 0.7760 0.337 0.58 0.36 0.06
#> SRR2139694 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139793 2 0.0000 0.995 0.00 1.00 0.00
#> SRR2139670 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139824 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139756 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139805 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139780 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139764 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139687 2 0.0000 0.995 0.00 1.00 0.00
#> SRR2139840 3 0.0000 0.996 0.00 0.00 1.00
#> SRR2139760 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139784 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139839 3 0.0000 0.996 0.00 0.00 1.00
#> SRR2139779 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139797 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139674 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139773 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139818 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139815 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139731 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139827 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139673 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139790 2 0.0000 0.995 0.00 1.00 0.00
#> SRR2139709 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139679 2 0.0000 0.995 0.00 1.00 0.00
#> SRR2139703 2 0.0000 0.995 0.00 1.00 0.00
#> SRR2139697 2 0.0892 0.976 0.00 0.98 0.02
#> SRR2139834 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139783 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139804 2 0.0000 0.995 0.00 1.00 0.00
#> SRR2139686 2 0.0000 0.995 0.00 1.00 0.00
#> SRR2139765 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139718 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139841 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139836 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139739 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139733 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139671 3 0.0000 0.996 0.00 0.00 1.00
#> SRR2139776 2 0.0000 0.995 0.00 1.00 0.00
#> SRR2139822 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139771 3 0.0000 0.996 0.00 0.00 1.00
#> SRR2139692 3 0.1529 0.952 0.04 0.00 0.96
#> SRR2139810 3 0.0000 0.996 0.00 0.00 1.00
#> SRR2139734 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139762 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139681 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139715 3 0.0000 0.996 0.00 0.00 1.00
#> SRR2139803 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139809 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139807 2 0.0000 0.995 0.00 1.00 0.00
#> SRR2139723 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139754 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139835 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139814 2 0.0000 0.995 0.00 1.00 0.00
#> SRR2139730 3 0.0000 0.996 0.00 0.00 1.00
#> SRR2139747 2 0.0000 0.995 0.00 1.00 0.00
#> SRR2139826 2 0.0000 0.995 0.00 1.00 0.00
#> SRR2139678 3 0.0000 0.996 0.00 0.00 1.00
#> SRR2139702 2 0.0000 0.995 0.00 1.00 0.00
#> SRR2139696 2 0.0000 0.995 0.00 1.00 0.00
#> SRR2139672 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139691 3 0.0000 0.996 0.00 0.00 1.00
#> SRR2139705 2 0.0000 0.995 0.00 1.00 0.00
#> SRR2139772 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139821 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139737 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139688 3 0.0000 0.996 0.00 0.00 1.00
#> SRR2139682 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139838 3 0.0000 0.996 0.00 0.00 1.00
#> SRR2139832 2 0.0000 0.995 0.00 1.00 0.00
#> SRR2139753 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139724 1 0.0000 0.990 1.00 0.00 0.00
#> SRR2139800 2 0.0000 0.995 0.00 1.00 0.00
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> SRR2140004 2 0.0000 0.98414 0.00 1.00 0.00 0.00
#> SRR2140036 1 0.2011 0.83130 0.92 0.00 0.00 0.08
#> SRR2139981 2 0.0000 0.98414 0.00 1.00 0.00 0.00
#> SRR2140035 2 0.0000 0.98414 0.00 1.00 0.00 0.00
#> SRR2139995 2 0.0000 0.98414 0.00 1.00 0.00 0.00
#> SRR2140069 2 0.0000 0.98414 0.00 1.00 0.00 0.00
#> SRR2140059 1 0.0000 0.82466 1.00 0.00 0.00 0.00
#> SRR2140072 2 0.0000 0.98414 0.00 1.00 0.00 0.00
#> SRR2140040 2 0.0000 0.98414 0.00 1.00 0.00 0.00
#> SRR2140008 2 0.1211 0.94704 0.00 0.96 0.00 0.04
#> SRR2140015 2 0.0000 0.98414 0.00 1.00 0.00 0.00
#> SRR2140027 2 0.0000 0.98414 0.00 1.00 0.00 0.00
#> SRR2140071 2 0.0000 0.98414 0.00 1.00 0.00 0.00
#> SRR2140039 2 0.0000 0.98414 0.00 1.00 0.00 0.00
#> SRR2139830 4 0.4713 0.47574 0.36 0.00 0.00 0.64
#> SRR2139726 4 0.3801 0.67887 0.22 0.00 0.00 0.78
#> SRR2139823 3 0.0000 0.99408 0.00 0.00 1.00 0.00
#> SRR2139693 1 0.4907 0.25702 0.58 0.00 0.00 0.42
#> SRR2139811 1 0.7674 -0.01874 0.46 0.26 0.00 0.28
#> SRR2139735 1 0.0707 0.81479 0.98 0.02 0.00 0.00
#> SRR2139694 1 0.2921 0.77826 0.86 0.00 0.00 0.14
#> SRR2139793 2 0.0000 0.98414 0.00 1.00 0.00 0.00
#> SRR2139670 4 0.0000 0.76099 0.00 0.00 0.00 1.00
#> SRR2139824 1 0.0707 0.83166 0.98 0.00 0.00 0.02
#> SRR2139756 1 0.0000 0.82466 1.00 0.00 0.00 0.00
#> SRR2139805 1 0.4855 0.32802 0.60 0.00 0.00 0.40
#> SRR2139780 4 0.4948 0.19984 0.44 0.00 0.00 0.56
#> SRR2139764 1 0.2921 0.78650 0.86 0.00 0.00 0.14
#> SRR2139687 2 0.0000 0.98414 0.00 1.00 0.00 0.00
#> SRR2139840 3 0.0000 0.99408 0.00 0.00 1.00 0.00
#> SRR2139760 4 0.4277 0.62957 0.28 0.00 0.00 0.72
#> SRR2139784 1 0.0000 0.82466 1.00 0.00 0.00 0.00
#> SRR2139839 3 0.0000 0.99408 0.00 0.00 1.00 0.00
#> SRR2139779 1 0.2647 0.80129 0.88 0.00 0.00 0.12
#> SRR2139797 4 0.0000 0.76099 0.00 0.00 0.00 1.00
#> SRR2139674 4 0.0000 0.76099 0.00 0.00 0.00 1.00
#> SRR2139773 4 0.0000 0.76099 0.00 0.00 0.00 1.00
#> SRR2139818 1 0.2345 0.82442 0.90 0.00 0.00 0.10
#> SRR2139815 1 0.2011 0.82216 0.92 0.00 0.00 0.08
#> SRR2139731 4 0.3400 0.70404 0.18 0.00 0.00 0.82
#> SRR2139827 4 0.4855 0.36245 0.40 0.00 0.00 0.60
#> SRR2139673 4 0.3975 0.62038 0.24 0.00 0.00 0.76
#> SRR2139790 2 0.0000 0.98414 0.00 1.00 0.00 0.00
#> SRR2139709 1 0.4994 0.06659 0.52 0.00 0.00 0.48
#> SRR2139679 2 0.0000 0.98414 0.00 1.00 0.00 0.00
#> SRR2139703 2 0.0000 0.98414 0.00 1.00 0.00 0.00
#> SRR2139697 2 0.1411 0.94987 0.02 0.96 0.02 0.00
#> SRR2139834 1 0.4977 -0.00861 0.54 0.00 0.00 0.46
#> SRR2139783 1 0.0000 0.82466 1.00 0.00 0.00 0.00
#> SRR2139804 2 0.0000 0.98414 0.00 1.00 0.00 0.00
#> SRR2139686 2 0.0000 0.98414 0.00 1.00 0.00 0.00
#> SRR2139765 4 0.0000 0.76099 0.00 0.00 0.00 1.00
#> SRR2139718 4 0.2647 0.73708 0.12 0.00 0.00 0.88
#> SRR2139841 1 0.2011 0.82990 0.92 0.00 0.00 0.08
#> SRR2139836 1 0.2921 0.79620 0.86 0.00 0.00 0.14
#> SRR2139739 4 0.4522 0.54531 0.32 0.00 0.00 0.68
#> SRR2139733 4 0.0707 0.75512 0.02 0.00 0.00 0.98
#> SRR2139671 3 0.0000 0.99408 0.00 0.00 1.00 0.00
#> SRR2139776 4 0.4134 0.53363 0.00 0.26 0.00 0.74
#> SRR2139822 1 0.2345 0.82442 0.90 0.00 0.00 0.10
#> SRR2139771 3 0.0000 0.99408 0.00 0.00 1.00 0.00
#> SRR2139692 1 0.3172 0.69358 0.84 0.00 0.16 0.00
#> SRR2139810 3 0.0000 0.99408 0.00 0.00 1.00 0.00
#> SRR2139734 1 0.2011 0.83130 0.92 0.00 0.00 0.08
#> SRR2139762 1 0.1211 0.82968 0.96 0.00 0.00 0.04
#> SRR2139681 1 0.0707 0.82680 0.98 0.00 0.00 0.02
#> SRR2139715 3 0.0000 0.99408 0.00 0.00 1.00 0.00
#> SRR2139803 4 0.4624 0.50315 0.34 0.00 0.00 0.66
#> SRR2139809 4 0.3801 0.67658 0.22 0.00 0.00 0.78
#> SRR2139807 2 0.0000 0.98414 0.00 1.00 0.00 0.00
#> SRR2139723 4 0.0000 0.76099 0.00 0.00 0.00 1.00
#> SRR2139754 4 0.4855 0.40467 0.40 0.00 0.00 0.60
#> SRR2139835 1 0.2345 0.82442 0.90 0.00 0.00 0.10
#> SRR2139814 2 0.0000 0.98414 0.00 1.00 0.00 0.00
#> SRR2139730 3 0.0000 0.99408 0.00 0.00 1.00 0.00
#> SRR2139747 2 0.6366 0.47856 0.12 0.64 0.00 0.24
#> SRR2139826 2 0.0000 0.98414 0.00 1.00 0.00 0.00
#> SRR2139678 3 0.0000 0.99408 0.00 0.00 1.00 0.00
#> SRR2139702 2 0.0000 0.98414 0.00 1.00 0.00 0.00
#> SRR2139696 2 0.0000 0.98414 0.00 1.00 0.00 0.00
#> SRR2139672 4 0.0000 0.76099 0.00 0.00 0.00 1.00
#> SRR2139691 3 0.0000 0.99408 0.00 0.00 1.00 0.00
#> SRR2139705 2 0.0000 0.98414 0.00 1.00 0.00 0.00
#> SRR2139772 1 0.2345 0.82442 0.90 0.00 0.00 0.10
#> SRR2139821 4 0.5000 0.08281 0.50 0.00 0.00 0.50
#> SRR2139737 1 0.2011 0.82990 0.92 0.00 0.00 0.08
#> SRR2139688 3 0.1913 0.93160 0.04 0.00 0.94 0.02
#> SRR2139682 1 0.0000 0.82466 1.00 0.00 0.00 0.00
#> SRR2139838 3 0.0000 0.99408 0.00 0.00 1.00 0.00
#> SRR2139832 2 0.0000 0.98414 0.00 1.00 0.00 0.00
#> SRR2139753 1 0.0707 0.83131 0.98 0.00 0.00 0.02
#> SRR2139724 4 0.0000 0.76099 0.00 0.00 0.00 1.00
#> SRR2139800 2 0.0000 0.98414 0.00 1.00 0.00 0.00
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
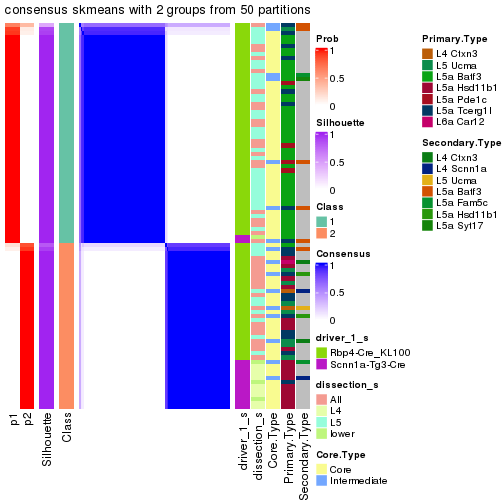
consensus_heatmap(res, k = 3)
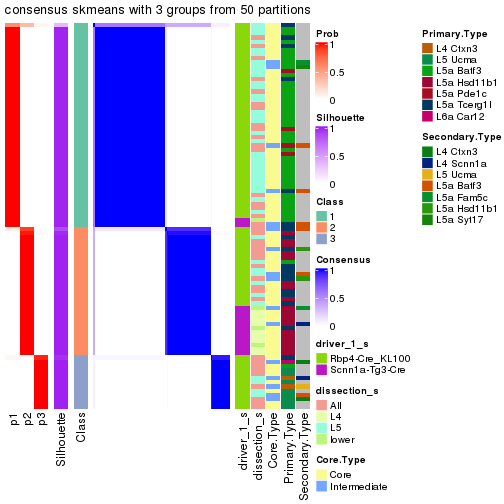
consensus_heatmap(res, k = 4)
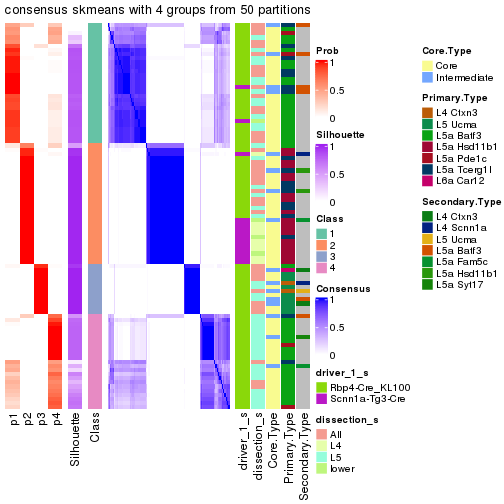
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
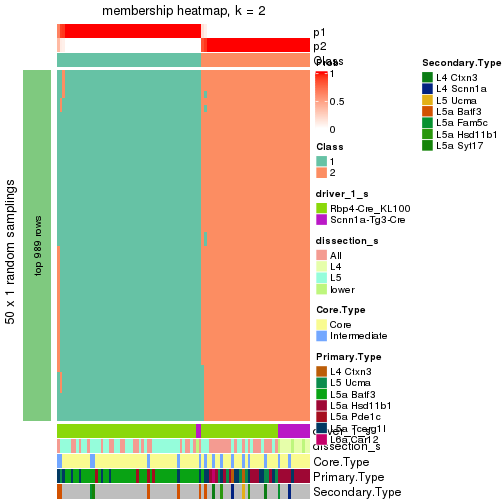
membership_heatmap(res, k = 3)
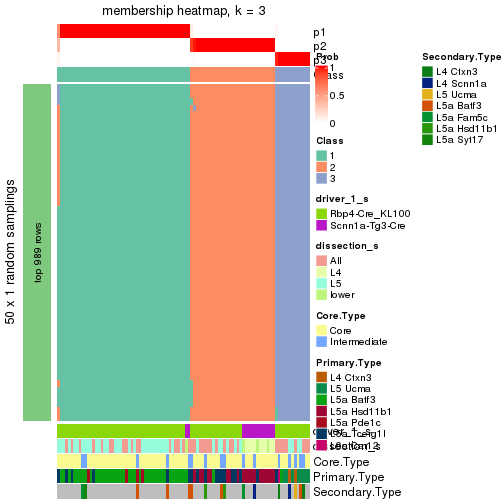
membership_heatmap(res, k = 4)
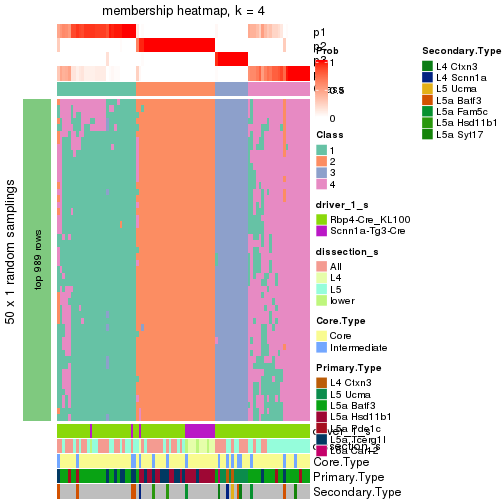
As soon as the classes for columns are determined, the signatures that are significantly different between subgroups can be looked for. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
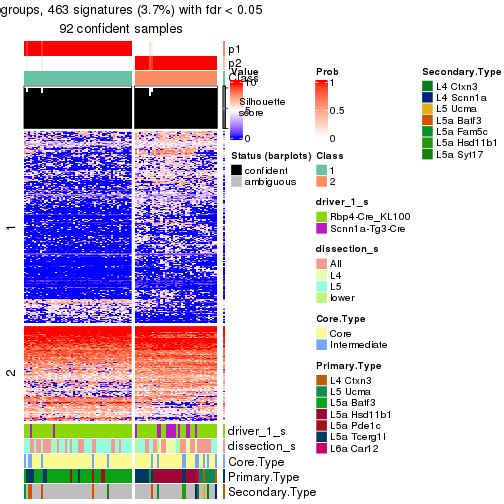
get_signatures(res, k = 3, scale_rows = FALSE)
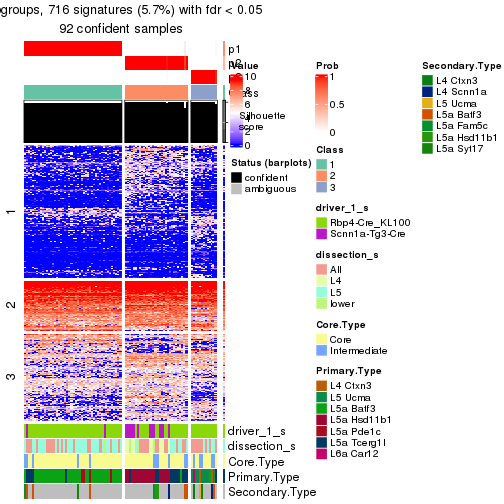
get_signatures(res, k = 4, scale_rows = FALSE)
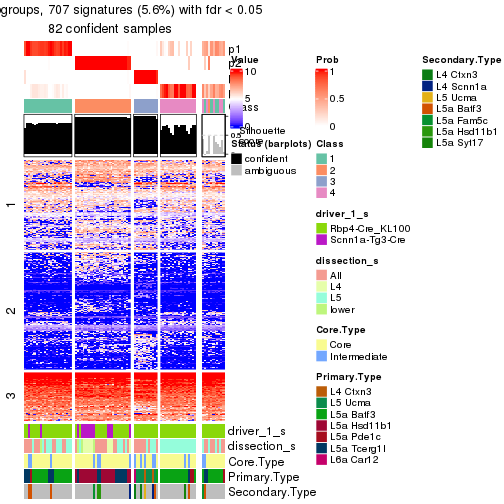
Compare the overlap of signatures from different k:
compare_signatures(res)
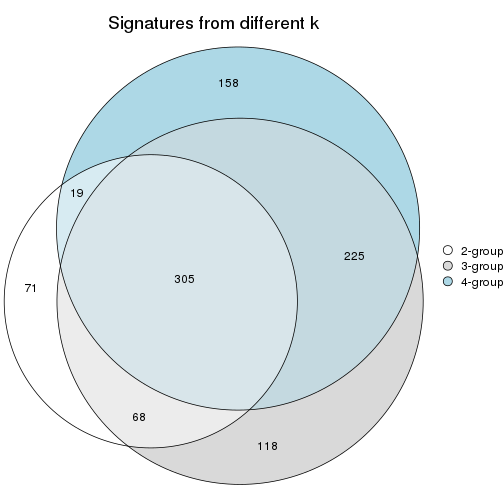
get_signature() returns a data frame invisibly. To get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows (which is done by automatically selecting number of clusters).If there are too many signatures, top_signatures = ... can be set to only show the
signatures with the highest FDRs:
# code only for demonstration
# e.g. to show the top 500 most significant rows
tb = get_signature(res, k = ..., top_signatures = 500)
If the signatures are defined as these which are uniquely high in current group, diff_method argument
can be set to "uniquely_high_in_one_group":
# code only for demonstration
tb = get_signature(res, k = ..., diff_method = "uniquely_high_in_one_group")
UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
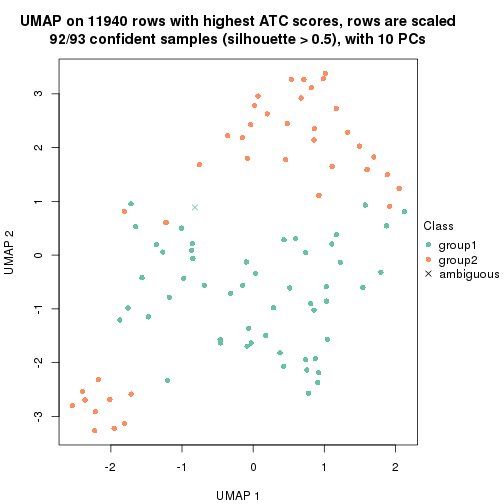
dimension_reduction(res, k = 3, method = "UMAP")
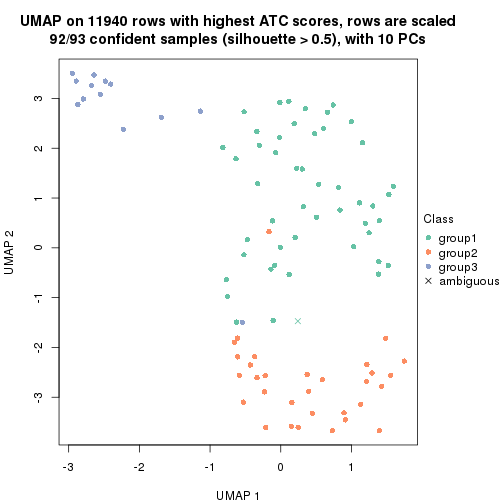
dimension_reduction(res, k = 4, method = "UMAP")
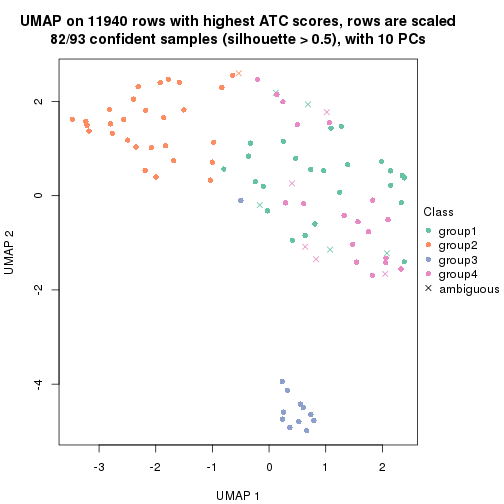
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
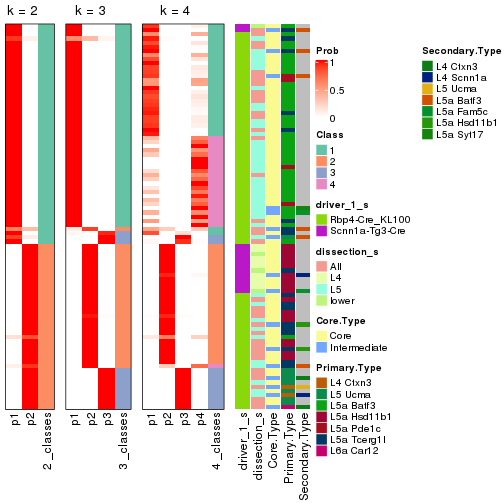
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n_sample driver_1_s(p-value) dissection_s(p-value) Core.Type(p-value)
#> ATC:skmeans 92 1.53e-03 1.45e-04 0.2601
#> ATC:skmeans 92 4.24e-05 2.37e-05 0.0571
#> ATC:skmeans 82 1.26e-04 2.86e-07 0.1075
#> Primary.Type(p-value) Secondary.Type(p-value) k
#> ATC:skmeans 1.20e-12 0.1241 2
#> ATC:skmeans 4.40e-25 0.0162 3
#> ATC:skmeans 6.38e-21 0.0346 4
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
Parent node: Node0. Child nodes: Node011-leaf , Node012-leaf , Node013-leaf , Node021 , Node022 , Node031-leaf , Node032-leaf , Node041-leaf , Node042-leaf .
The object with results only for a single top-value method and a single partitioning method can be extracted as:
res = res_rh["02"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4.
#> On a matrix with 11940 rows and 124 columns.
#> Top rows (1194) are extracted by 'ATC' method.
#> Subgroups are detected by 'skmeans' method.
#> Performed in total 150 partitions by row resampling.
#> Best k for subgroups seems to be 4.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_partitions"
#> [7] "compare_signatures" "consensus_heatmap" "dimension_reduction"
#> [10] "functional_enrichment" "get_anno_col" "get_anno"
#> [13] "get_classes" "get_consensus" "get_matrix"
#> [16] "get_membership" "get_param" "get_signatures"
#> [19] "get_stats" "is_best_k" "is_stable_k"
#> [22] "membership_heatmap" "ncol" "nrow"
#> [25] "plot_ecdf" "predict_classes" "rownames"
#> [28] "select_partition_number" "show" "suggest_best_k"
#> [31] "test_to_known_factors" "top_rows_heatmap"
collect_plots() function collects all the plots made from res for all k (number of subgroups)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
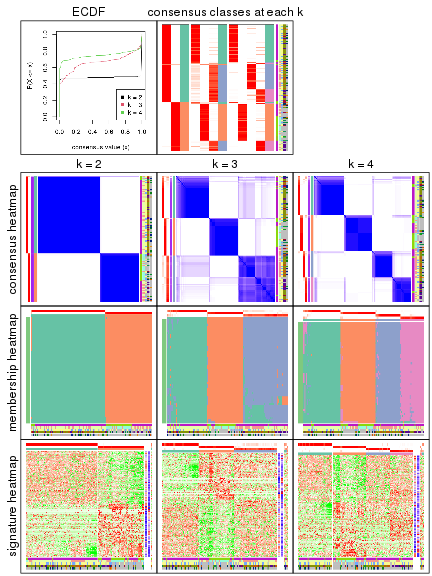
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, higher 1-PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
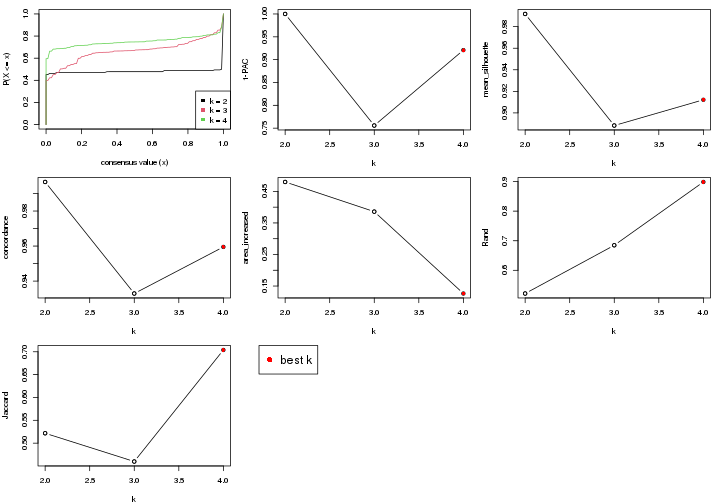
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 1.000 0.992 0.997 0.480 0.522 0.522
#> 3 3 0.756 0.888 0.933 0.386 0.685 0.460
#> 4 4 0.921 0.912 0.960 0.126 0.899 0.704
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 4
#> attr(,"optional")
#> [1] 2
There is also optional best \(k\) = 2 that is worth to check.
Following is the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall subgroup
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> SRR2140028 1 0.000 0.995 1.00 0.00
#> SRR2140022 1 0.000 0.995 1.00 0.00
#> SRR2140055 2 0.000 0.998 0.00 1.00
#> SRR2140083 2 0.000 0.998 0.00 1.00
#> SRR2139991 1 0.000 0.995 1.00 0.00
#> SRR2140067 1 0.000 0.995 1.00 0.00
#> SRR2140010 1 0.000 0.995 1.00 0.00
#> SRR2140031 1 0.000 0.995 1.00 0.00
#> SRR2140046 2 0.000 0.998 0.00 1.00
#> SRR2140074 1 0.000 0.995 1.00 0.00
#> SRR2140003 1 0.000 0.995 1.00 0.00
#> SRR2139988 2 0.000 0.998 0.00 1.00
#> SRR2139982 1 0.000 0.995 1.00 0.00
#> SRR2140009 1 0.000 0.995 1.00 0.00
#> SRR2140073 1 0.000 0.995 1.00 0.00
#> SRR2139985 1 0.000 0.995 1.00 0.00
#> SRR2140079 2 0.000 0.998 0.00 1.00
#> SRR2140041 2 0.000 0.998 0.00 1.00
#> SRR2140084 2 0.000 0.998 0.00 1.00
#> SRR2139978 1 0.000 0.995 1.00 0.00
#> SRR2139996 1 0.000 0.995 1.00 0.00
#> SRR2140017 1 0.000 0.995 1.00 0.00
#> SRR2140060 1 0.000 0.995 1.00 0.00
#> SRR2140058 1 0.000 0.995 1.00 0.00
#> SRR2140052 1 0.000 0.995 1.00 0.00
#> SRR2140025 1 0.000 0.995 1.00 0.00
#> SRR2140056 1 0.000 0.995 1.00 0.00
#> SRR2140021 1 0.000 0.995 1.00 0.00
#> SRR2140013 1 0.000 0.995 1.00 0.00
#> SRR2140064 1 0.000 0.995 1.00 0.00
#> SRR2139998 1 0.000 0.995 1.00 0.00
#> SRR2139992 1 0.000 0.995 1.00 0.00
#> SRR2140019 1 0.000 0.995 1.00 0.00
#> SRR2140080 2 0.000 0.998 0.00 1.00
#> SRR2140045 1 0.000 0.995 1.00 0.00
#> SRR2140032 1 0.000 0.995 1.00 0.00
#> SRR2140000 1 0.000 0.995 1.00 0.00
#> SRR2140077 2 0.000 0.998 0.00 1.00
#> SRR2139986 1 0.000 0.995 1.00 0.00
#> SRR2140070 1 0.000 0.995 1.00 0.00
#> SRR2140007 1 0.000 0.995 1.00 0.00
#> SRR2140048 1 0.000 0.995 1.00 0.00
#> SRR2140042 1 0.000 0.995 1.00 0.00
#> SRR2140063 2 0.000 0.998 0.00 1.00
#> SRR2140014 1 0.000 0.995 1.00 0.00
#> SRR2140026 1 0.000 0.995 1.00 0.00
#> SRR2140051 1 0.000 0.995 1.00 0.00
#> SRR2140061 1 0.000 0.995 1.00 0.00
#> SRR2140016 2 0.000 0.998 0.00 1.00
#> SRR2139979 1 0.000 0.995 1.00 0.00
#> SRR2139997 2 0.327 0.936 0.06 0.94
#> SRR2140085 2 0.000 0.998 0.00 1.00
#> SRR2140024 1 0.000 0.995 1.00 0.00
#> SRR2140053 1 0.000 0.995 1.00 0.00
#> SRR2140078 2 0.000 0.998 0.00 1.00
#> SRR2139984 1 0.000 0.995 1.00 0.00
#> SRR2140005 1 0.000 0.995 1.00 0.00
#> SRR2140047 2 0.000 0.998 0.00 1.00
#> SRR2140030 1 0.000 0.995 1.00 0.00
#> SRR2139983 1 0.000 0.995 1.00 0.00
#> SRR2139989 1 0.000 0.995 1.00 0.00
#> SRR2140002 1 0.000 0.995 1.00 0.00
#> SRR2140075 1 0.000 0.995 1.00 0.00
#> SRR2140054 2 0.000 0.998 0.00 1.00
#> SRR2140023 1 0.000 0.995 1.00 0.00
#> SRR2140029 1 0.000 0.995 1.00 0.00
#> SRR2140011 1 0.000 0.995 1.00 0.00
#> SRR2140066 1 0.000 0.995 1.00 0.00
#> SRR2139990 1 0.000 0.995 1.00 0.00
#> SRR2140082 2 0.000 0.998 0.00 1.00
#> SRR2140086 2 0.000 0.998 0.00 1.00
#> SRR2140068 1 0.000 0.995 1.00 0.00
#> SRR2139994 1 0.000 0.995 1.00 0.00
#> SRR2140062 2 0.000 0.998 0.00 1.00
#> SRR2140050 1 0.000 0.995 1.00 0.00
#> SRR2140006 1 0.000 0.995 1.00 0.00
#> SRR2139987 1 0.000 0.995 1.00 0.00
#> SRR2140043 1 0.000 0.995 1.00 0.00
#> SRR2140034 1 0.000 0.995 1.00 0.00
#> SRR2140049 1 0.000 0.995 1.00 0.00
#> SRR2140033 1 0.000 0.995 1.00 0.00
#> SRR2140044 1 0.000 0.995 1.00 0.00
#> SRR2140076 2 0.000 0.998 0.00 1.00
#> SRR2140001 1 0.000 0.995 1.00 0.00
#> SRR2139980 1 0.000 0.995 1.00 0.00
#> SRR2140020 1 0.000 0.995 1.00 0.00
#> SRR2140057 1 0.000 0.995 1.00 0.00
#> SRR2140018 2 0.000 0.998 0.00 1.00
#> SRR2140081 2 0.000 0.998 0.00 1.00
#> SRR2139993 1 0.000 0.995 1.00 0.00
#> SRR2139999 1 0.000 0.995 1.00 0.00
#> SRR2139977 1 0.000 0.995 1.00 0.00
#> SRR2140065 1 0.000 0.995 1.00 0.00
#> SRR2140012 1 0.000 0.995 1.00 0.00
#> SRR2139847 2 0.000 0.998 0.00 1.00
#> SRR2139802 2 0.000 0.998 0.00 1.00
#> SRR2139751 2 0.000 0.998 0.00 1.00
#> SRR2139854 2 0.000 0.998 0.00 1.00
#> SRR2139770 2 0.000 0.998 0.00 1.00
#> SRR2139853 2 0.000 0.998 0.00 1.00
#> SRR2139721 2 0.000 0.998 0.00 1.00
#> SRR2139669 1 0.000 0.995 1.00 0.00
#> SRR2139844 2 0.000 0.998 0.00 1.00
#> SRR2139801 2 0.000 0.998 0.00 1.00
#> SRR2139704 2 0.000 0.998 0.00 1.00
#> SRR2139812 1 0.000 0.995 1.00 0.00
#> SRR2139746 1 0.000 0.995 1.00 0.00
#> SRR2139850 2 0.000 0.998 0.00 1.00
#> SRR2139843 2 0.000 0.998 0.00 1.00
#> SRR2139849 2 0.000 0.998 0.00 1.00
#> SRR2139684 1 0.925 0.484 0.66 0.34
#> SRR2139852 2 0.000 0.998 0.00 1.00
#> SRR2139855 2 0.000 0.998 0.00 1.00
#> SRR2139698 2 0.000 0.998 0.00 1.00
#> SRR2139846 2 0.000 0.998 0.00 1.00
#> SRR2139729 2 0.141 0.979 0.02 0.98
#> SRR2139842 2 0.000 0.998 0.00 1.00
#> SRR2139851 2 0.000 0.998 0.00 1.00
#> SRR2139813 2 0.000 0.998 0.00 1.00
#> SRR2139845 2 0.000 0.998 0.00 1.00
#> SRR2139333 2 0.000 0.998 0.00 1.00
#> SRR2139383 2 0.000 0.998 0.00 1.00
#> SRR2139384 2 0.000 0.998 0.00 1.00
#> SRR2139325 2 0.000 0.998 0.00 1.00
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> SRR2140028 3 0.3686 0.8631 0.14 0.00 0.86
#> SRR2140022 1 0.0000 0.9447 1.00 0.00 0.00
#> SRR2140055 2 0.0000 0.9839 0.00 1.00 0.00
#> SRR2140083 3 0.3340 0.8073 0.00 0.12 0.88
#> SRR2139991 1 0.0000 0.9447 1.00 0.00 0.00
#> SRR2140067 3 0.4291 0.8467 0.18 0.00 0.82
#> SRR2140010 1 0.0000 0.9447 1.00 0.00 0.00
#> SRR2140031 1 0.2066 0.8948 0.94 0.00 0.06
#> SRR2140046 2 0.0000 0.9839 0.00 1.00 0.00
#> SRR2140074 1 0.0000 0.9447 1.00 0.00 0.00
#> SRR2140003 1 0.0000 0.9447 1.00 0.00 0.00
#> SRR2139988 3 0.3042 0.8496 0.04 0.04 0.92
#> SRR2139982 3 0.2066 0.8747 0.06 0.00 0.94
#> SRR2140009 1 0.0000 0.9447 1.00 0.00 0.00
#> SRR2140073 1 0.0000 0.9447 1.00 0.00 0.00
#> SRR2139985 1 0.0892 0.9294 0.98 0.00 0.02
#> SRR2140079 2 0.0000 0.9839 0.00 1.00 0.00
#> SRR2140041 2 0.0000 0.9839 0.00 1.00 0.00
#> SRR2140084 3 0.2537 0.8373 0.00 0.08 0.92
#> SRR2139978 3 0.2537 0.8493 0.08 0.00 0.92
#> SRR2139996 1 0.0000 0.9447 1.00 0.00 0.00
#> SRR2140017 3 0.3340 0.8691 0.12 0.00 0.88
#> SRR2140060 3 0.4555 0.8375 0.20 0.00 0.80
#> SRR2140058 3 0.4291 0.8467 0.18 0.00 0.82
#> SRR2140052 3 0.4291 0.8467 0.18 0.00 0.82
#> SRR2140025 1 0.0000 0.9447 1.00 0.00 0.00
#> SRR2140056 3 0.4291 0.8467 0.18 0.00 0.82
#> SRR2140021 3 0.3340 0.8714 0.12 0.00 0.88
#> SRR2140013 3 0.1529 0.8736 0.04 0.00 0.96
#> SRR2140064 3 0.4291 0.8467 0.18 0.00 0.82
#> SRR2139998 1 0.0000 0.9447 1.00 0.00 0.00
#> SRR2139992 1 0.0000 0.9447 1.00 0.00 0.00
#> SRR2140019 1 0.6309 0.0151 0.50 0.00 0.50
#> SRR2140080 2 0.0000 0.9839 0.00 1.00 0.00
#> SRR2140045 3 0.3340 0.8691 0.12 0.00 0.88
#> SRR2140032 1 0.1529 0.9111 0.96 0.00 0.04
#> SRR2140000 1 0.0000 0.9447 1.00 0.00 0.00
#> SRR2140077 2 0.0892 0.9723 0.00 0.98 0.02
#> SRR2139986 1 0.0000 0.9447 1.00 0.00 0.00
#> SRR2140070 1 0.0000 0.9447 1.00 0.00 0.00
#> SRR2140007 1 0.2959 0.8626 0.90 0.00 0.10
#> SRR2140048 3 0.5216 0.7620 0.26 0.00 0.74
#> SRR2140042 3 0.4291 0.8467 0.18 0.00 0.82
#> SRR2140063 3 0.2537 0.8373 0.00 0.08 0.92
#> SRR2140014 1 0.0000 0.9447 1.00 0.00 0.00
#> SRR2140026 3 0.0000 0.8625 0.00 0.00 1.00
#> SRR2140051 3 0.5016 0.7862 0.24 0.00 0.76
#> SRR2140061 1 0.2066 0.8948 0.94 0.00 0.06
#> SRR2140016 3 0.2537 0.8373 0.00 0.08 0.92
#> SRR2139979 3 0.0892 0.8645 0.02 0.00 0.98
#> SRR2139997 3 0.6045 0.3474 0.38 0.00 0.62
#> SRR2140085 2 0.0000 0.9839 0.00 1.00 0.00
#> SRR2140024 1 0.0000 0.9447 1.00 0.00 0.00
#> SRR2140053 3 0.4291 0.8467 0.18 0.00 0.82
#> SRR2140078 2 0.0892 0.9723 0.00 0.98 0.02
#> SRR2139984 1 0.0000 0.9447 1.00 0.00 0.00
#> SRR2140005 1 0.0000 0.9447 1.00 0.00 0.00
#> SRR2140047 3 0.2537 0.8373 0.00 0.08 0.92
#> SRR2140030 3 0.4291 0.7598 0.18 0.00 0.82
#> SRR2139983 1 0.5216 0.6614 0.74 0.00 0.26
#> SRR2139989 1 0.0000 0.9447 1.00 0.00 0.00
#> SRR2140002 3 0.2066 0.8750 0.06 0.00 0.94
#> SRR2140075 1 0.0000 0.9447 1.00 0.00 0.00
#> SRR2140054 2 0.0000 0.9839 0.00 1.00 0.00
#> SRR2140023 1 0.4555 0.7327 0.80 0.00 0.20
#> SRR2140029 1 0.0000 0.9447 1.00 0.00 0.00
#> SRR2140011 3 0.2066 0.8749 0.06 0.00 0.94
#> SRR2140066 3 0.4555 0.8296 0.20 0.00 0.80
#> SRR2139990 1 0.0000 0.9447 1.00 0.00 0.00
#> SRR2140082 3 0.4796 0.6827 0.00 0.22 0.78
#> SRR2140086 2 0.0892 0.9723 0.00 0.98 0.02
#> SRR2140068 1 0.0000 0.9447 1.00 0.00 0.00
#> SRR2139994 1 0.4555 0.7478 0.80 0.00 0.20
#> SRR2140062 3 0.0000 0.8625 0.00 0.00 1.00
#> SRR2140050 3 0.0000 0.8625 0.00 0.00 1.00
#> SRR2140006 3 0.2537 0.8493 0.08 0.00 0.92
#> SRR2139987 1 0.0000 0.9447 1.00 0.00 0.00
#> SRR2140043 3 0.3686 0.8631 0.14 0.00 0.86
#> SRR2140034 1 0.0000 0.9447 1.00 0.00 0.00
#> SRR2140049 3 0.4291 0.8467 0.18 0.00 0.82
#> SRR2140033 3 0.2537 0.8493 0.08 0.00 0.92
#> SRR2140044 3 0.4291 0.8467 0.18 0.00 0.82
#> SRR2140076 2 0.0892 0.9723 0.00 0.98 0.02
#> SRR2140001 3 0.0892 0.8645 0.02 0.00 0.98
#> SRR2139980 3 0.1529 0.8708 0.04 0.00 0.96
#> SRR2140020 1 0.0000 0.9447 1.00 0.00 0.00
#> SRR2140057 3 0.4291 0.8467 0.18 0.00 0.82
#> SRR2140018 3 0.2537 0.8373 0.00 0.08 0.92
#> SRR2140081 2 0.0000 0.9839 0.00 1.00 0.00
#> SRR2139993 1 0.0000 0.9447 1.00 0.00 0.00
#> SRR2139999 3 0.1529 0.8736 0.04 0.00 0.96
#> SRR2139977 3 0.3340 0.8536 0.12 0.00 0.88
#> SRR2140065 3 0.5216 0.7606 0.26 0.00 0.74
#> SRR2140012 1 0.0000 0.9447 1.00 0.00 0.00
#> SRR2139847 2 0.0000 0.9839 0.00 1.00 0.00
#> SRR2139802 2 0.0000 0.9839 0.00 1.00 0.00
#> SRR2139751 2 0.1529 0.9571 0.00 0.96 0.04
#> SRR2139854 2 0.0000 0.9839 0.00 1.00 0.00
#> SRR2139770 2 0.1529 0.9571 0.00 0.96 0.04
#> SRR2139853 2 0.0000 0.9839 0.00 1.00 0.00
#> SRR2139721 2 0.0000 0.9839 0.00 1.00 0.00
#> SRR2139669 1 0.0000 0.9447 1.00 0.00 0.00
#> SRR2139844 2 0.0000 0.9839 0.00 1.00 0.00
#> SRR2139801 2 0.0000 0.9839 0.00 1.00 0.00
#> SRR2139704 2 0.0000 0.9839 0.00 1.00 0.00
#> SRR2139812 1 0.0892 0.9294 0.98 0.00 0.02
#> SRR2139746 3 0.0892 0.8692 0.02 0.00 0.98
#> SRR2139850 2 0.0000 0.9839 0.00 1.00 0.00
#> SRR2139843 2 0.0000 0.9839 0.00 1.00 0.00
#> SRR2139849 2 0.0000 0.9839 0.00 1.00 0.00
#> SRR2139684 2 0.6045 0.3679 0.00 0.62 0.38
#> SRR2139852 2 0.0000 0.9839 0.00 1.00 0.00
#> SRR2139855 2 0.0000 0.9839 0.00 1.00 0.00
#> SRR2139698 2 0.1529 0.9571 0.00 0.96 0.04
#> SRR2139846 2 0.0000 0.9839 0.00 1.00 0.00
#> SRR2139729 1 0.4002 0.7816 0.84 0.16 0.00
#> SRR2139842 2 0.0000 0.9839 0.00 1.00 0.00
#> SRR2139851 2 0.0000 0.9839 0.00 1.00 0.00
#> SRR2139813 1 0.8803 0.4899 0.58 0.18 0.24
#> SRR2139845 2 0.0000 0.9839 0.00 1.00 0.00
#> SRR2139333 2 0.0000 0.9839 0.00 1.00 0.00
#> SRR2139383 2 0.0000 0.9839 0.00 1.00 0.00
#> SRR2139384 2 0.0000 0.9839 0.00 1.00 0.00
#> SRR2139325 2 0.0000 0.9839 0.00 1.00 0.00
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> SRR2140028 3 0.0000 0.958 0.00 0.00 1.00 0.00
#> SRR2140022 1 0.0000 0.951 1.00 0.00 0.00 0.00
#> SRR2140055 2 0.0000 0.969 0.00 1.00 0.00 0.00
#> SRR2140083 4 0.0000 0.947 0.00 0.00 0.00 1.00
#> SRR2139991 1 0.1637 0.905 0.94 0.00 0.06 0.00
#> SRR2140067 3 0.0000 0.958 0.00 0.00 1.00 0.00
#> SRR2140010 1 0.0000 0.951 1.00 0.00 0.00 0.00
#> SRR2140031 1 0.4522 0.530 0.68 0.00 0.32 0.00
#> SRR2140046 2 0.0707 0.967 0.00 0.98 0.00 0.02
#> SRR2140074 1 0.0000 0.951 1.00 0.00 0.00 0.00
#> SRR2140003 1 0.0000 0.951 1.00 0.00 0.00 0.00
#> SRR2139988 4 0.0000 0.947 0.00 0.00 0.00 1.00
#> SRR2139982 4 0.3853 0.809 0.02 0.00 0.16 0.82
#> SRR2140009 1 0.0000 0.951 1.00 0.00 0.00 0.00
#> SRR2140073 1 0.0000 0.951 1.00 0.00 0.00 0.00
#> SRR2139985 1 0.2345 0.865 0.90 0.00 0.10 0.00
#> SRR2140079 2 0.0707 0.967 0.00 0.98 0.00 0.02
#> SRR2140041 2 0.0707 0.967 0.00 0.98 0.00 0.02
#> SRR2140084 4 0.0000 0.947 0.00 0.00 0.00 1.00
#> SRR2139978 4 0.0707 0.944 0.02 0.00 0.00 0.98
#> SRR2139996 1 0.0000 0.951 1.00 0.00 0.00 0.00
#> SRR2140017 3 0.0000 0.958 0.00 0.00 1.00 0.00
#> SRR2140060 3 0.2647 0.840 0.00 0.00 0.88 0.12
#> SRR2140058 3 0.0000 0.958 0.00 0.00 1.00 0.00
#> SRR2140052 3 0.0000 0.958 0.00 0.00 1.00 0.00
#> SRR2140025 1 0.0000 0.951 1.00 0.00 0.00 0.00
#> SRR2140056 3 0.0000 0.958 0.00 0.00 1.00 0.00
#> SRR2140021 3 0.5657 0.674 0.16 0.00 0.72 0.12
#> SRR2140013 3 0.0000 0.958 0.00 0.00 1.00 0.00
#> SRR2140064 3 0.0000 0.958 0.00 0.00 1.00 0.00
#> SRR2139998 1 0.0000 0.951 1.00 0.00 0.00 0.00
#> SRR2139992 1 0.0000 0.951 1.00 0.00 0.00 0.00
#> SRR2140019 4 0.1211 0.931 0.04 0.00 0.00 0.96
#> SRR2140080 2 0.0707 0.967 0.00 0.98 0.00 0.02
#> SRR2140045 3 0.0000 0.958 0.00 0.00 1.00 0.00
#> SRR2140032 1 0.0000 0.951 1.00 0.00 0.00 0.00
#> SRR2140000 1 0.0000 0.951 1.00 0.00 0.00 0.00
#> SRR2140077 2 0.0707 0.967 0.00 0.98 0.00 0.02
#> SRR2139986 1 0.0000 0.951 1.00 0.00 0.00 0.00
#> SRR2140070 1 0.0000 0.951 1.00 0.00 0.00 0.00
#> SRR2140007 1 0.2647 0.844 0.88 0.00 0.00 0.12
#> SRR2140048 3 0.0000 0.958 0.00 0.00 1.00 0.00
#> SRR2140042 3 0.0000 0.958 0.00 0.00 1.00 0.00
#> SRR2140063 4 0.0000 0.947 0.00 0.00 0.00 1.00
#> SRR2140014 1 0.0000 0.951 1.00 0.00 0.00 0.00
#> SRR2140026 4 0.0707 0.943 0.00 0.00 0.02 0.98
#> SRR2140051 3 0.0000 0.958 0.00 0.00 1.00 0.00
#> SRR2140061 3 0.4134 0.637 0.26 0.00 0.74 0.00
#> SRR2140016 4 0.0000 0.947 0.00 0.00 0.00 1.00
#> SRR2139979 4 0.1211 0.933 0.00 0.00 0.04 0.96
#> SRR2139997 4 0.0707 0.944 0.02 0.00 0.00 0.98
#> SRR2140085 2 0.0707 0.967 0.00 0.98 0.00 0.02
#> SRR2140024 1 0.0000 0.951 1.00 0.00 0.00 0.00
#> SRR2140053 3 0.0000 0.958 0.00 0.00 1.00 0.00
#> SRR2140078 2 0.0707 0.967 0.00 0.98 0.00 0.02
#> SRR2139984 1 0.0000 0.951 1.00 0.00 0.00 0.00
#> SRR2140005 1 0.0000 0.951 1.00 0.00 0.00 0.00
#> SRR2140047 4 0.0000 0.947 0.00 0.00 0.00 1.00
#> SRR2140030 4 0.0707 0.944 0.02 0.00 0.00 0.98
#> SRR2139983 1 0.4948 0.231 0.56 0.00 0.00 0.44
#> SRR2139989 1 0.0000 0.951 1.00 0.00 0.00 0.00
#> SRR2140002 3 0.4134 0.625 0.00 0.00 0.74 0.26
#> SRR2140075 1 0.0000 0.951 1.00 0.00 0.00 0.00
#> SRR2140054 2 0.0000 0.969 0.00 1.00 0.00 0.00
#> SRR2140023 1 0.3975 0.683 0.76 0.00 0.00 0.24
#> SRR2140029 1 0.0000 0.951 1.00 0.00 0.00 0.00
#> SRR2140011 4 0.2921 0.846 0.00 0.00 0.14 0.86
#> SRR2140066 3 0.0000 0.958 0.00 0.00 1.00 0.00
#> SRR2139990 1 0.0000 0.951 1.00 0.00 0.00 0.00
#> SRR2140082 4 0.0000 0.947 0.00 0.00 0.00 1.00
#> SRR2140086 2 0.0707 0.967 0.00 0.98 0.00 0.02
#> SRR2140068 1 0.0000 0.951 1.00 0.00 0.00 0.00
#> SRR2139994 1 0.4790 0.405 0.62 0.00 0.00 0.38
#> SRR2140062 4 0.0000 0.947 0.00 0.00 0.00 1.00
#> SRR2140050 4 0.4948 0.220 0.00 0.00 0.44 0.56
#> SRR2140006 4 0.0707 0.944 0.02 0.00 0.00 0.98
#> SRR2139987 1 0.0000 0.951 1.00 0.00 0.00 0.00
#> SRR2140043 3 0.0000 0.958 0.00 0.00 1.00 0.00
#> SRR2140034 1 0.0000 0.951 1.00 0.00 0.00 0.00
#> SRR2140049 3 0.0000 0.958 0.00 0.00 1.00 0.00
#> SRR2140033 4 0.0707 0.944 0.02 0.00 0.00 0.98
#> SRR2140044 3 0.0000 0.958 0.00 0.00 1.00 0.00
#> SRR2140076 2 0.0707 0.967 0.00 0.98 0.00 0.02
#> SRR2140001 4 0.1411 0.938 0.02 0.00 0.02 0.96
#> SRR2139980 4 0.2921 0.845 0.00 0.00 0.14 0.86
#> SRR2140020 1 0.0000 0.951 1.00 0.00 0.00 0.00
#> SRR2140057 3 0.0000 0.958 0.00 0.00 1.00 0.00
#> SRR2140018 4 0.0000 0.947 0.00 0.00 0.00 1.00
#> SRR2140081 2 0.0707 0.967 0.00 0.98 0.00 0.02
#> SRR2139993 1 0.1211 0.923 0.96 0.00 0.04 0.00
#> SRR2139999 3 0.0707 0.941 0.00 0.00 0.98 0.02
#> SRR2139977 4 0.1913 0.925 0.04 0.00 0.02 0.94
#> SRR2140065 3 0.0000 0.958 0.00 0.00 1.00 0.00
#> SRR2140012 1 0.0000 0.951 1.00 0.00 0.00 0.00
#> SRR2139847 2 0.0000 0.969 0.00 1.00 0.00 0.00
#> SRR2139802 2 0.0000 0.969 0.00 1.00 0.00 0.00
#> SRR2139751 2 0.3400 0.782 0.00 0.82 0.00 0.18
#> SRR2139854 2 0.0000 0.969 0.00 1.00 0.00 0.00
#> SRR2139770 2 0.4790 0.411 0.00 0.62 0.00 0.38
#> SRR2139853 2 0.0000 0.969 0.00 1.00 0.00 0.00
#> SRR2139721 2 0.0000 0.969 0.00 1.00 0.00 0.00
#> SRR2139669 1 0.0000 0.951 1.00 0.00 0.00 0.00
#> SRR2139844 2 0.0000 0.969 0.00 1.00 0.00 0.00
#> SRR2139801 2 0.0000 0.969 0.00 1.00 0.00 0.00
#> SRR2139704 2 0.0000 0.969 0.00 1.00 0.00 0.00
#> SRR2139812 1 0.0000 0.951 1.00 0.00 0.00 0.00
#> SRR2139746 4 0.0707 0.943 0.00 0.00 0.02 0.98
#> SRR2139850 2 0.0000 0.969 0.00 1.00 0.00 0.00
#> SRR2139843 2 0.0707 0.967 0.00 0.98 0.00 0.02
#> SRR2139849 2 0.0000 0.969 0.00 1.00 0.00 0.00
#> SRR2139684 3 0.0000 0.958 0.00 0.00 1.00 0.00
#> SRR2139852 2 0.0000 0.969 0.00 1.00 0.00 0.00
#> SRR2139855 2 0.0000 0.969 0.00 1.00 0.00 0.00
#> SRR2139698 2 0.3975 0.694 0.00 0.76 0.00 0.24
#> SRR2139846 2 0.0707 0.967 0.00 0.98 0.00 0.02
#> SRR2139729 1 0.1211 0.919 0.96 0.04 0.00 0.00
#> SRR2139842 2 0.0707 0.967 0.00 0.98 0.00 0.02
#> SRR2139851 2 0.0000 0.969 0.00 1.00 0.00 0.00
#> SRR2139813 4 0.0707 0.940 0.00 0.02 0.00 0.98
#> SRR2139845 2 0.0000 0.969 0.00 1.00 0.00 0.00
#> SRR2139333 2 0.0000 0.969 0.00 1.00 0.00 0.00
#> SRR2139383 2 0.0707 0.967 0.00 0.98 0.00 0.02
#> SRR2139384 2 0.0707 0.967 0.00 0.98 0.00 0.02
#> SRR2139325 2 0.0000 0.969 0.00 1.00 0.00 0.00
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
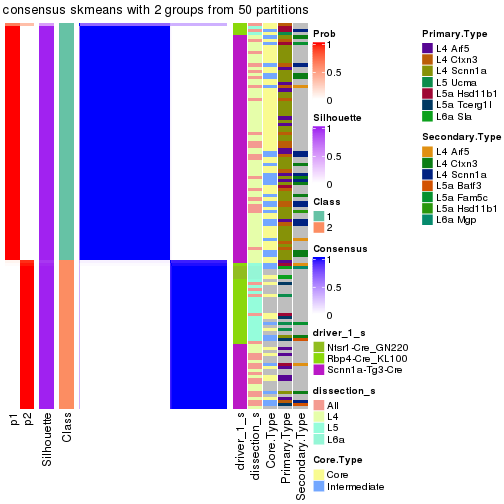
consensus_heatmap(res, k = 3)
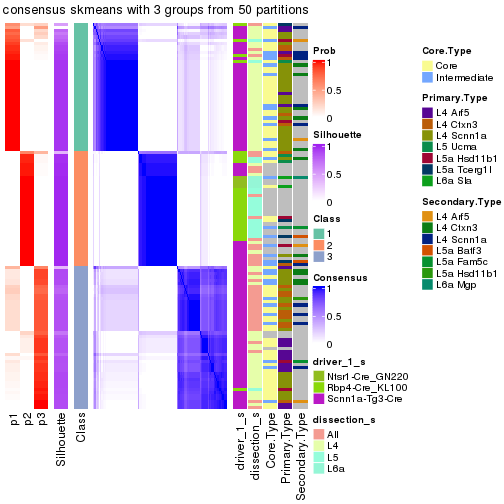
consensus_heatmap(res, k = 4)
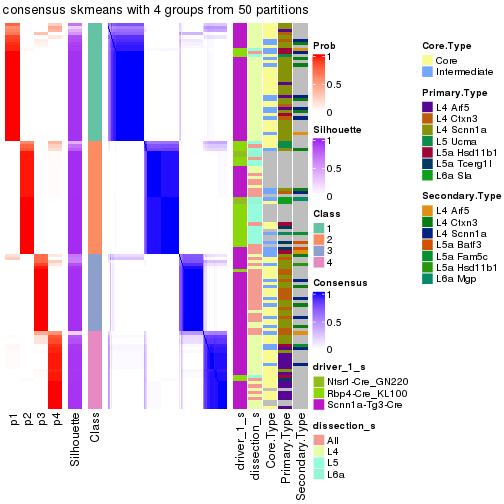
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
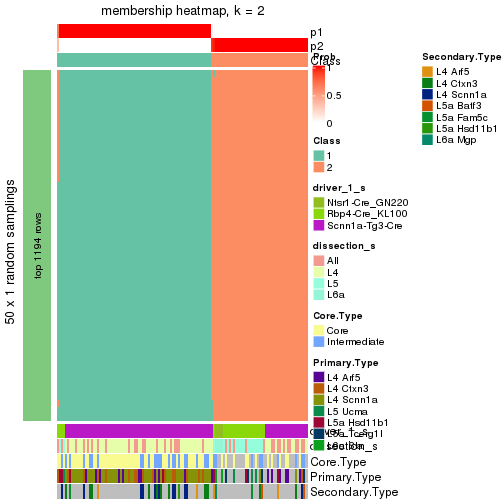
membership_heatmap(res, k = 3)
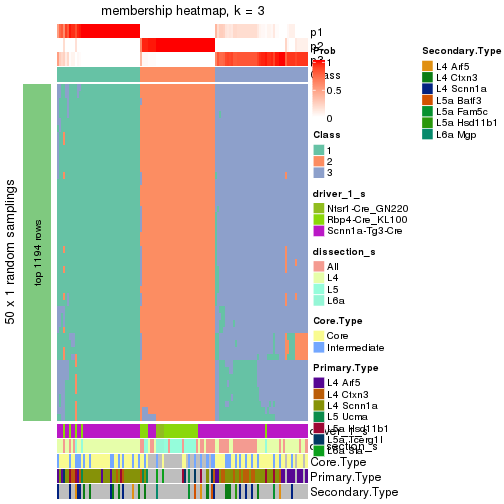
membership_heatmap(res, k = 4)
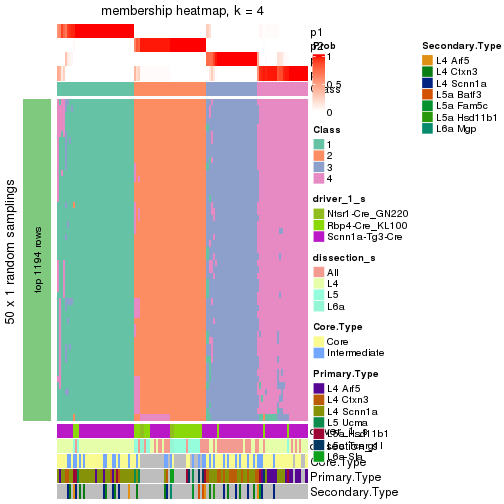
As soon as the classes for columns are determined, the signatures that are significantly different between subgroups can be looked for. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
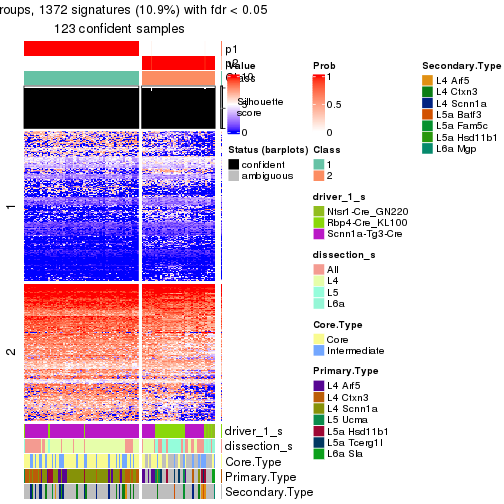
get_signatures(res, k = 3, scale_rows = FALSE)
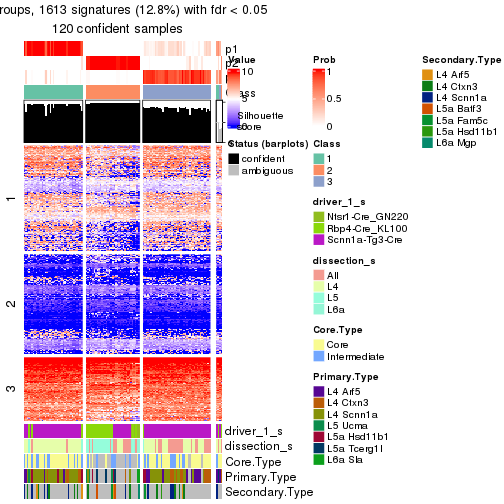
get_signatures(res, k = 4, scale_rows = FALSE)
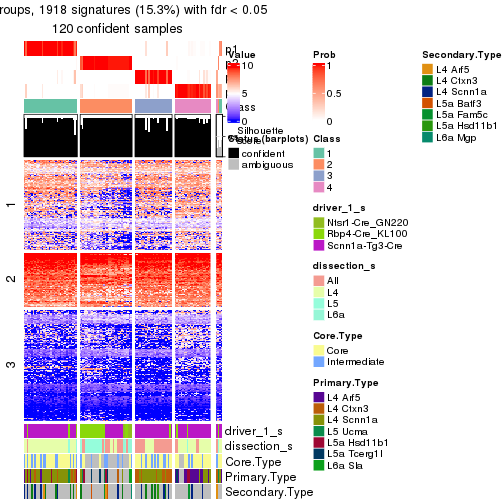
Compare the overlap of signatures from different k:
compare_signatures(res)
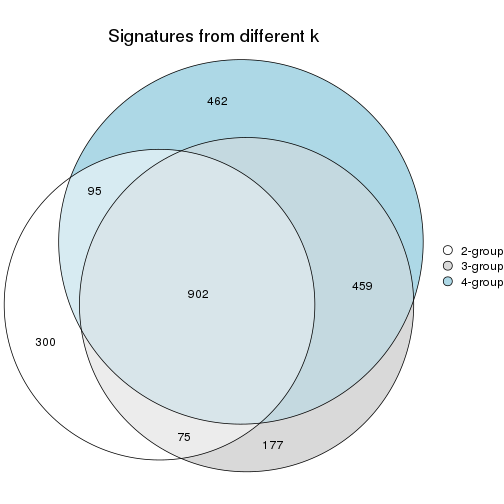
get_signature() returns a data frame invisibly. To get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows (which is done by automatically selecting number of clusters).If there are too many signatures, top_signatures = ... can be set to only show the
signatures with the highest FDRs:
# code only for demonstration
# e.g. to show the top 500 most significant rows
tb = get_signature(res, k = ..., top_signatures = 500)
If the signatures are defined as these which are uniquely high in current group, diff_method argument
can be set to "uniquely_high_in_one_group":
# code only for demonstration
tb = get_signature(res, k = ..., diff_method = "uniquely_high_in_one_group")
UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
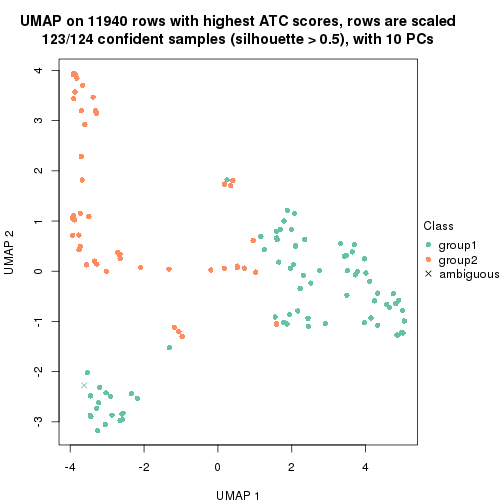
dimension_reduction(res, k = 3, method = "UMAP")
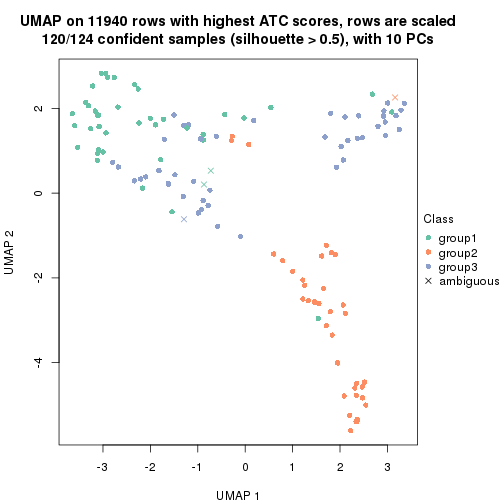
dimension_reduction(res, k = 4, method = "UMAP")
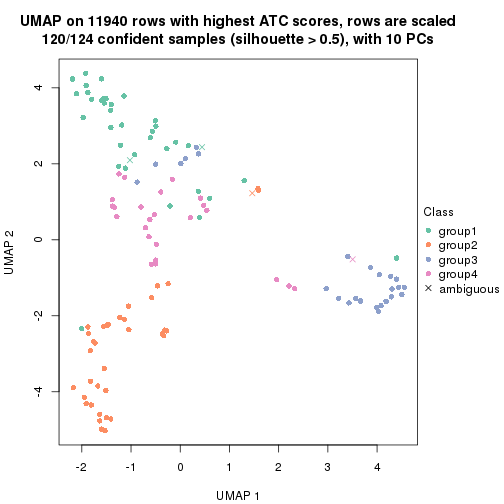
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
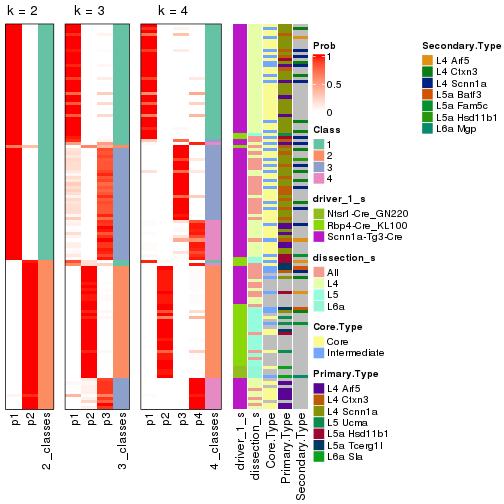
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n_sample driver_1_s(p-value) dissection_s(p-value) Core.Type(p-value)
#> ATC:skmeans 123 1.20e-09 1.15e-08 0.5218
#> ATC:skmeans 120 3.52e-11 2.42e-13 0.0562
#> ATC:skmeans 120 1.35e-08 3.91e-16 0.0234
#> Primary.Type(p-value) Secondary.Type(p-value) k
#> ATC:skmeans 1.06e-07 0.0411 2
#> ATC:skmeans 3.67e-08 0.0256 3
#> ATC:skmeans 7.78e-13 0.0158 4
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
Parent node: Node02. Child nodes: Node0211-leaf , Node0212-leaf , Node0221 , Node0222-leaf .
The object with results only for a single top-value method and a single partitioning method can be extracted as:
res = res_rh["021"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4.
#> On a matrix with 11878 rows and 76 columns.
#> Top rows (913) are extracted by 'ATC' method.
#> Subgroups are detected by 'skmeans' method.
#> Performed in total 150 partitions by row resampling.
#> Best k for subgroups seems to be 3.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_partitions"
#> [7] "compare_signatures" "consensus_heatmap" "dimension_reduction"
#> [10] "functional_enrichment" "get_anno_col" "get_anno"
#> [13] "get_classes" "get_consensus" "get_matrix"
#> [16] "get_membership" "get_param" "get_signatures"
#> [19] "get_stats" "is_best_k" "is_stable_k"
#> [22] "membership_heatmap" "ncol" "nrow"
#> [25] "plot_ecdf" "predict_classes" "rownames"
#> [28] "select_partition_number" "show" "suggest_best_k"
#> [31] "test_to_known_factors" "top_rows_heatmap"
collect_plots() function collects all the plots made from res for all k (number of subgroups)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
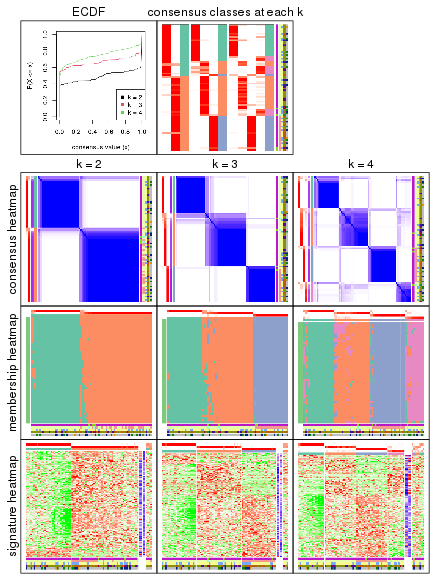
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, higher 1-PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
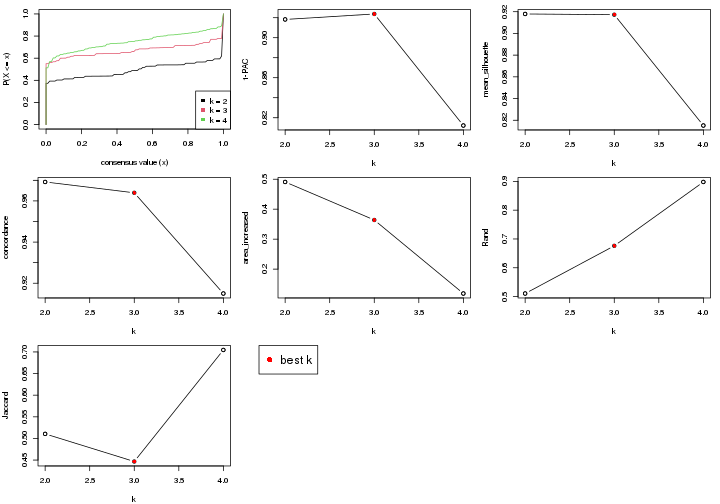
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 0.918 0.918 0.969 0.491 0.511 0.511
#> 3 3 0.924 0.917 0.964 0.364 0.676 0.447
#> 4 4 0.812 0.815 0.915 0.119 0.898 0.705
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 3
#> attr(,"optional")
#> [1] 2
There is also optional best \(k\) = 2 that is worth to check.
Following is the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall subgroup
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> SRR2140028 2 0.000 0.9676 0.00 1.00
#> SRR2140022 1 0.000 0.9657 1.00 0.00
#> SRR2139991 1 0.000 0.9657 1.00 0.00
#> SRR2140067 2 0.000 0.9676 0.00 1.00
#> SRR2140010 2 0.999 0.0615 0.48 0.52
#> SRR2140031 1 0.000 0.9657 1.00 0.00
#> SRR2140074 1 0.000 0.9657 1.00 0.00
#> SRR2140003 1 0.000 0.9657 1.00 0.00
#> SRR2139982 2 0.000 0.9676 0.00 1.00
#> SRR2140009 1 0.000 0.9657 1.00 0.00
#> SRR2140073 1 0.000 0.9657 1.00 0.00
#> SRR2139985 2 0.327 0.9131 0.06 0.94
#> SRR2139978 2 0.000 0.9676 0.00 1.00
#> SRR2139996 1 0.000 0.9657 1.00 0.00
#> SRR2140017 2 0.000 0.9676 0.00 1.00
#> SRR2140060 2 0.000 0.9676 0.00 1.00
#> SRR2140058 2 0.000 0.9676 0.00 1.00
#> SRR2140052 2 0.000 0.9676 0.00 1.00
#> SRR2140025 1 0.000 0.9657 1.00 0.00
#> SRR2140056 2 0.000 0.9676 0.00 1.00
#> SRR2140021 2 0.000 0.9676 0.00 1.00
#> SRR2140013 2 0.000 0.9676 0.00 1.00
#> SRR2140064 2 0.000 0.9676 0.00 1.00
#> SRR2139998 1 0.000 0.9657 1.00 0.00
#> SRR2139992 1 0.000 0.9657 1.00 0.00
#> SRR2140019 2 0.469 0.8698 0.10 0.90
#> SRR2140045 2 0.000 0.9676 0.00 1.00
#> SRR2140032 1 0.000 0.9657 1.00 0.00
#> SRR2140000 1 0.000 0.9657 1.00 0.00
#> SRR2139986 1 0.000 0.9657 1.00 0.00
#> SRR2140070 1 0.000 0.9657 1.00 0.00
#> SRR2140007 1 0.958 0.3751 0.62 0.38
#> SRR2140048 2 0.000 0.9676 0.00 1.00
#> SRR2140042 2 0.000 0.9676 0.00 1.00
#> SRR2140014 1 0.000 0.9657 1.00 0.00
#> SRR2140026 2 0.000 0.9676 0.00 1.00
#> SRR2140051 2 0.000 0.9676 0.00 1.00
#> SRR2140061 2 0.995 0.1301 0.46 0.54
#> SRR2139979 2 0.000 0.9676 0.00 1.00
#> SRR2140024 1 0.000 0.9657 1.00 0.00
#> SRR2140053 2 0.000 0.9676 0.00 1.00
#> SRR2139984 1 0.000 0.9657 1.00 0.00
#> SRR2140005 1 0.000 0.9657 1.00 0.00
#> SRR2140030 2 0.141 0.9509 0.02 0.98
#> SRR2139983 2 0.000 0.9676 0.00 1.00
#> SRR2139989 1 0.000 0.9657 1.00 0.00
#> SRR2140002 2 0.000 0.9676 0.00 1.00
#> SRR2140075 1 0.000 0.9657 1.00 0.00
#> SRR2140023 1 0.990 0.2016 0.56 0.44
#> SRR2140029 2 0.760 0.7052 0.22 0.78
#> SRR2140011 2 0.000 0.9676 0.00 1.00
#> SRR2140066 2 0.000 0.9676 0.00 1.00
#> SRR2139990 1 0.000 0.9657 1.00 0.00
#> SRR2140068 1 0.000 0.9657 1.00 0.00
#> SRR2139994 1 0.000 0.9657 1.00 0.00
#> SRR2140050 2 0.000 0.9676 0.00 1.00
#> SRR2140006 2 0.000 0.9676 0.00 1.00
#> SRR2139987 1 0.000 0.9657 1.00 0.00
#> SRR2140043 2 0.000 0.9676 0.00 1.00
#> SRR2140034 1 0.000 0.9657 1.00 0.00
#> SRR2140049 2 0.000 0.9676 0.00 1.00
#> SRR2140033 2 0.000 0.9676 0.00 1.00
#> SRR2140044 2 0.000 0.9676 0.00 1.00
#> SRR2140001 2 0.000 0.9676 0.00 1.00
#> SRR2139980 2 0.000 0.9676 0.00 1.00
#> SRR2140020 1 0.000 0.9657 1.00 0.00
#> SRR2140057 2 0.000 0.9676 0.00 1.00
#> SRR2139993 1 0.634 0.7941 0.84 0.16
#> SRR2139999 2 0.000 0.9676 0.00 1.00
#> SRR2139977 2 0.000 0.9676 0.00 1.00
#> SRR2140065 2 0.000 0.9676 0.00 1.00
#> SRR2140012 1 0.000 0.9657 1.00 0.00
#> SRR2139669 2 0.141 0.9508 0.02 0.98
#> SRR2139812 2 0.000 0.9676 0.00 1.00
#> SRR2139746 2 0.000 0.9676 0.00 1.00
#> SRR2139684 2 0.000 0.9676 0.00 1.00
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> SRR2140028 2 0.000 0.919 0.00 1.00 0.00
#> SRR2140022 1 0.000 0.994 1.00 0.00 0.00
#> SRR2139991 2 0.619 0.354 0.42 0.58 0.00
#> SRR2140067 3 0.000 0.992 0.00 0.00 1.00
#> SRR2140010 2 0.000 0.919 0.00 1.00 0.00
#> SRR2140031 3 0.254 0.912 0.08 0.00 0.92
#> SRR2140074 1 0.000 0.994 1.00 0.00 0.00
#> SRR2140003 1 0.000 0.994 1.00 0.00 0.00
#> SRR2139982 2 0.000 0.919 0.00 1.00 0.00
#> SRR2140009 1 0.000 0.994 1.00 0.00 0.00
#> SRR2140073 1 0.000 0.994 1.00 0.00 0.00
#> SRR2139985 2 0.000 0.919 0.00 1.00 0.00
#> SRR2139978 2 0.000 0.919 0.00 1.00 0.00
#> SRR2139996 1 0.000 0.994 1.00 0.00 0.00
#> SRR2140017 2 0.000 0.919 0.00 1.00 0.00
#> SRR2140060 3 0.000 0.992 0.00 0.00 1.00
#> SRR2140058 3 0.000 0.992 0.00 0.00 1.00
#> SRR2140052 3 0.000 0.992 0.00 0.00 1.00
#> SRR2140025 1 0.000 0.994 1.00 0.00 0.00
#> SRR2140056 3 0.000 0.992 0.00 0.00 1.00
#> SRR2140021 2 0.000 0.919 0.00 1.00 0.00
#> SRR2140013 2 0.153 0.895 0.00 0.96 0.04
#> SRR2140064 3 0.000 0.992 0.00 0.00 1.00
#> SRR2139998 2 0.631 0.113 0.50 0.50 0.00
#> SRR2139992 1 0.000 0.994 1.00 0.00 0.00
#> SRR2140019 2 0.000 0.919 0.00 1.00 0.00
#> SRR2140045 3 0.000 0.992 0.00 0.00 1.00
#> SRR2140032 2 0.540 0.629 0.28 0.72 0.00
#> SRR2140000 1 0.000 0.994 1.00 0.00 0.00
#> SRR2139986 1 0.000 0.994 1.00 0.00 0.00
#> SRR2140070 1 0.000 0.994 1.00 0.00 0.00
#> SRR2140007 2 0.000 0.919 0.00 1.00 0.00
#> SRR2140048 3 0.000 0.992 0.00 0.00 1.00
#> SRR2140042 3 0.000 0.992 0.00 0.00 1.00
#> SRR2140014 1 0.334 0.851 0.88 0.12 0.00
#> SRR2140026 2 0.000 0.919 0.00 1.00 0.00
#> SRR2140051 3 0.000 0.992 0.00 0.00 1.00
#> SRR2140061 3 0.000 0.992 0.00 0.00 1.00
#> SRR2139979 2 0.000 0.919 0.00 1.00 0.00
#> SRR2140024 1 0.000 0.994 1.00 0.00 0.00
#> SRR2140053 3 0.000 0.992 0.00 0.00 1.00
#> SRR2139984 1 0.000 0.994 1.00 0.00 0.00
#> SRR2140005 1 0.000 0.994 1.00 0.00 0.00
#> SRR2140030 2 0.295 0.869 0.02 0.92 0.06
#> SRR2139983 2 0.000 0.919 0.00 1.00 0.00
#> SRR2139989 1 0.000 0.994 1.00 0.00 0.00
#> SRR2140002 2 0.000 0.919 0.00 1.00 0.00
#> SRR2140075 1 0.000 0.994 1.00 0.00 0.00
#> SRR2140023 2 0.000 0.919 0.00 1.00 0.00
#> SRR2140029 2 0.000 0.919 0.00 1.00 0.00
#> SRR2140011 2 0.000 0.919 0.00 1.00 0.00
#> SRR2140066 3 0.000 0.992 0.00 0.00 1.00
#> SRR2139990 1 0.000 0.994 1.00 0.00 0.00
#> SRR2140068 1 0.000 0.994 1.00 0.00 0.00
#> SRR2139994 2 0.369 0.812 0.14 0.86 0.00
#> SRR2140050 3 0.000 0.992 0.00 0.00 1.00
#> SRR2140006 2 0.000 0.919 0.00 1.00 0.00
#> SRR2139987 2 0.630 0.179 0.48 0.52 0.00
#> SRR2140043 3 0.000 0.992 0.00 0.00 1.00
#> SRR2140034 1 0.000 0.994 1.00 0.00 0.00
#> SRR2140049 3 0.000 0.992 0.00 0.00 1.00
#> SRR2140033 2 0.000 0.919 0.00 1.00 0.00
#> SRR2140044 3 0.000 0.992 0.00 0.00 1.00
#> SRR2140001 2 0.000 0.919 0.00 1.00 0.00
#> SRR2139980 2 0.000 0.919 0.00 1.00 0.00
#> SRR2140020 1 0.000 0.994 1.00 0.00 0.00
#> SRR2140057 3 0.000 0.992 0.00 0.00 1.00
#> SRR2139993 2 0.400 0.793 0.16 0.84 0.00
#> SRR2139999 2 0.254 0.862 0.00 0.92 0.08
#> SRR2139977 2 0.000 0.919 0.00 1.00 0.00
#> SRR2140065 3 0.000 0.992 0.00 0.00 1.00
#> SRR2140012 1 0.000 0.994 1.00 0.00 0.00
#> SRR2139669 2 0.540 0.597 0.00 0.72 0.28
#> SRR2139812 3 0.254 0.911 0.00 0.08 0.92
#> SRR2139746 2 0.000 0.919 0.00 1.00 0.00
#> SRR2139684 3 0.000 0.992 0.00 0.00 1.00
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> SRR2140028 4 0.4642 0.6371 0.00 0.24 0.02 0.74
#> SRR2140022 1 0.6104 0.5613 0.68 0.18 0.00 0.14
#> SRR2139991 4 0.0707 0.8523 0.02 0.00 0.00 0.98
#> SRR2140067 3 0.0000 0.9567 0.00 0.00 1.00 0.00
#> SRR2140010 2 0.4790 0.4764 0.00 0.62 0.00 0.38
#> SRR2140031 3 0.6074 0.3971 0.34 0.00 0.60 0.06
#> SRR2140074 1 0.0000 0.9165 1.00 0.00 0.00 0.00
#> SRR2140003 1 0.0000 0.9165 1.00 0.00 0.00 0.00
#> SRR2139982 2 0.0000 0.8690 0.00 1.00 0.00 0.00
#> SRR2140009 1 0.0000 0.9165 1.00 0.00 0.00 0.00
#> SRR2140073 1 0.0000 0.9165 1.00 0.00 0.00 0.00
#> SRR2139985 4 0.1211 0.8394 0.00 0.04 0.00 0.96
#> SRR2139978 2 0.0000 0.8690 0.00 1.00 0.00 0.00
#> SRR2139996 4 0.4977 0.0728 0.46 0.00 0.00 0.54
#> SRR2140017 2 0.2921 0.8144 0.00 0.86 0.00 0.14
#> SRR2140060 3 0.0000 0.9567 0.00 0.00 1.00 0.00
#> SRR2140058 3 0.0000 0.9567 0.00 0.00 1.00 0.00
#> SRR2140052 3 0.0000 0.9567 0.00 0.00 1.00 0.00
#> SRR2140025 1 0.2011 0.8440 0.92 0.00 0.00 0.08
#> SRR2140056 3 0.0000 0.9567 0.00 0.00 1.00 0.00
#> SRR2140021 4 0.4642 0.6504 0.00 0.24 0.02 0.74
#> SRR2140013 2 0.7382 0.3331 0.00 0.52 0.22 0.26
#> SRR2140064 3 0.0000 0.9567 0.00 0.00 1.00 0.00
#> SRR2139998 4 0.0707 0.8523 0.02 0.00 0.00 0.98
#> SRR2139992 4 0.1211 0.8461 0.04 0.00 0.00 0.96
#> SRR2140019 2 0.0707 0.8651 0.00 0.98 0.00 0.02
#> SRR2140045 3 0.0000 0.9567 0.00 0.00 1.00 0.00
#> SRR2140032 2 0.3525 0.7933 0.04 0.86 0.00 0.10
#> SRR2140000 1 0.0000 0.9165 1.00 0.00 0.00 0.00
#> SRR2139986 1 0.4907 0.2425 0.58 0.00 0.00 0.42
#> SRR2140070 1 0.0000 0.9165 1.00 0.00 0.00 0.00
#> SRR2140007 2 0.3801 0.7245 0.00 0.78 0.00 0.22
#> SRR2140048 3 0.0000 0.9567 0.00 0.00 1.00 0.00
#> SRR2140042 3 0.0000 0.9567 0.00 0.00 1.00 0.00
#> SRR2140014 1 0.6005 0.0487 0.50 0.46 0.00 0.04
#> SRR2140026 2 0.2647 0.8196 0.00 0.88 0.00 0.12
#> SRR2140051 3 0.0000 0.9567 0.00 0.00 1.00 0.00
#> SRR2140061 3 0.1211 0.9193 0.04 0.00 0.96 0.00
#> SRR2139979 2 0.0000 0.8690 0.00 1.00 0.00 0.00
#> SRR2140024 1 0.0000 0.9165 1.00 0.00 0.00 0.00
#> SRR2140053 3 0.0000 0.9567 0.00 0.00 1.00 0.00
#> SRR2139984 4 0.1637 0.8333 0.06 0.00 0.00 0.94
#> SRR2140005 1 0.0000 0.9165 1.00 0.00 0.00 0.00
#> SRR2140030 2 0.3106 0.8338 0.04 0.90 0.02 0.04
#> SRR2139983 2 0.0000 0.8690 0.00 1.00 0.00 0.00
#> SRR2139989 1 0.0000 0.9165 1.00 0.00 0.00 0.00
#> SRR2140002 2 0.2345 0.8335 0.00 0.90 0.00 0.10
#> SRR2140075 1 0.0000 0.9165 1.00 0.00 0.00 0.00
#> SRR2140023 2 0.3400 0.7834 0.00 0.82 0.00 0.18
#> SRR2140029 2 0.1211 0.8594 0.00 0.96 0.00 0.04
#> SRR2140011 2 0.3400 0.7709 0.00 0.82 0.00 0.18
#> SRR2140066 3 0.0000 0.9567 0.00 0.00 1.00 0.00
#> SRR2139990 1 0.0000 0.9165 1.00 0.00 0.00 0.00
#> SRR2140068 1 0.0000 0.9165 1.00 0.00 0.00 0.00
#> SRR2139994 4 0.0707 0.8466 0.00 0.02 0.00 0.98
#> SRR2140050 3 0.0000 0.9567 0.00 0.00 1.00 0.00
#> SRR2140006 2 0.0000 0.8690 0.00 1.00 0.00 0.00
#> SRR2139987 4 0.1913 0.8438 0.02 0.04 0.00 0.94
#> SRR2140043 3 0.0000 0.9567 0.00 0.00 1.00 0.00
#> SRR2140034 1 0.0000 0.9165 1.00 0.00 0.00 0.00
#> SRR2140049 3 0.0000 0.9567 0.00 0.00 1.00 0.00
#> SRR2140033 2 0.0707 0.8625 0.00 0.98 0.00 0.02
#> SRR2140044 3 0.0000 0.9567 0.00 0.00 1.00 0.00
#> SRR2140001 2 0.2345 0.8368 0.00 0.90 0.00 0.10
#> SRR2139980 2 0.0000 0.8690 0.00 1.00 0.00 0.00
#> SRR2140020 1 0.0000 0.9165 1.00 0.00 0.00 0.00
#> SRR2140057 3 0.0000 0.9567 0.00 0.00 1.00 0.00
#> SRR2139993 4 0.0707 0.8523 0.02 0.00 0.00 0.98
#> SRR2139999 2 0.6881 0.3815 0.00 0.54 0.34 0.12
#> SRR2139977 2 0.0000 0.8690 0.00 1.00 0.00 0.00
#> SRR2140065 3 0.0000 0.9567 0.00 0.00 1.00 0.00
#> SRR2140012 1 0.0000 0.9165 1.00 0.00 0.00 0.00
#> SRR2139669 4 0.6089 0.5644 0.00 0.28 0.08 0.64
#> SRR2139812 3 0.6623 0.3839 0.06 0.32 0.60 0.02
#> SRR2139746 2 0.0000 0.8690 0.00 1.00 0.00 0.00
#> SRR2139684 3 0.0000 0.9567 0.00 0.00 1.00 0.00
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
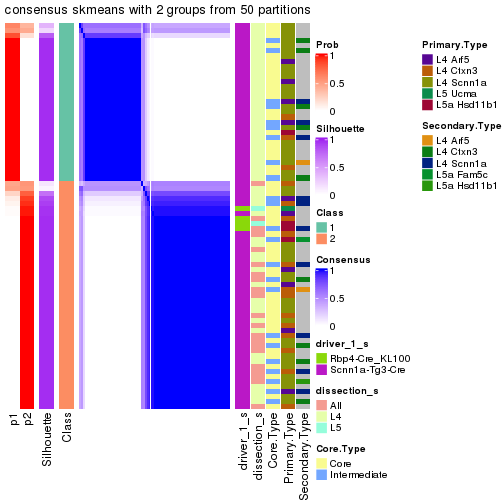
consensus_heatmap(res, k = 3)
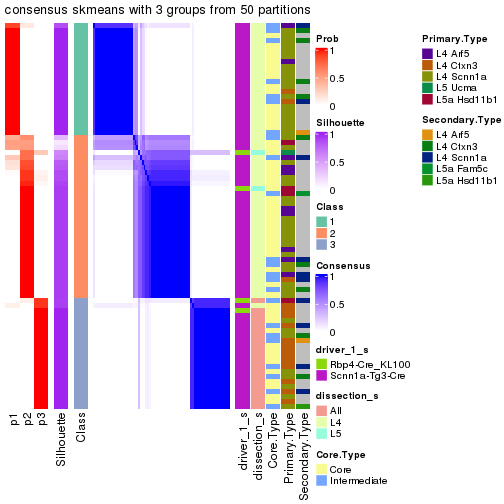
consensus_heatmap(res, k = 4)
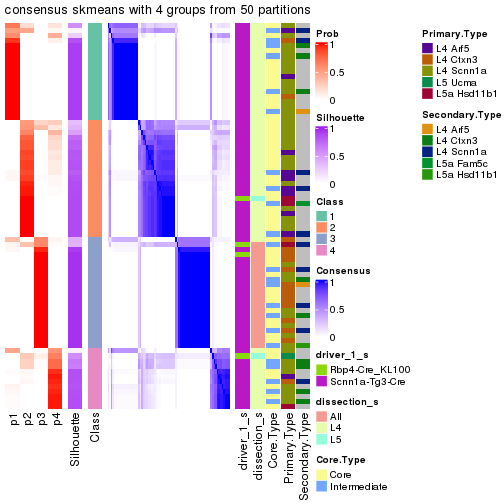
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
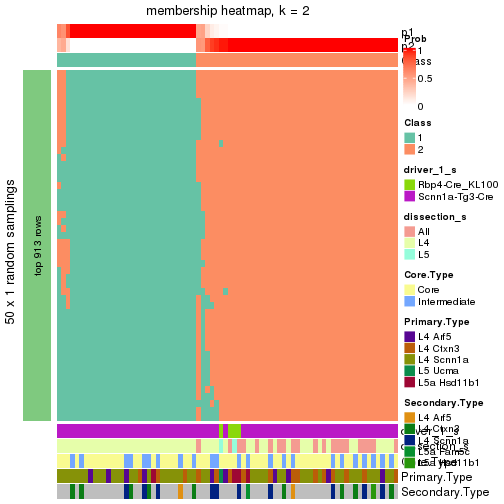
membership_heatmap(res, k = 3)
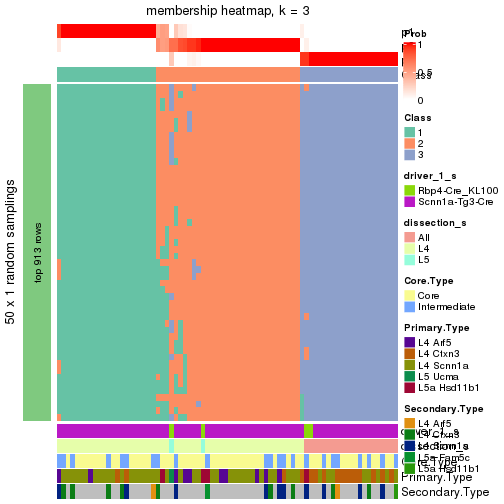
membership_heatmap(res, k = 4)
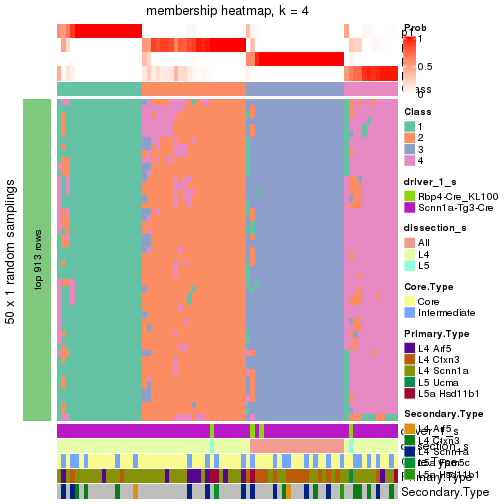
As soon as the classes for columns are determined, the signatures that are significantly different between subgroups can be looked for. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
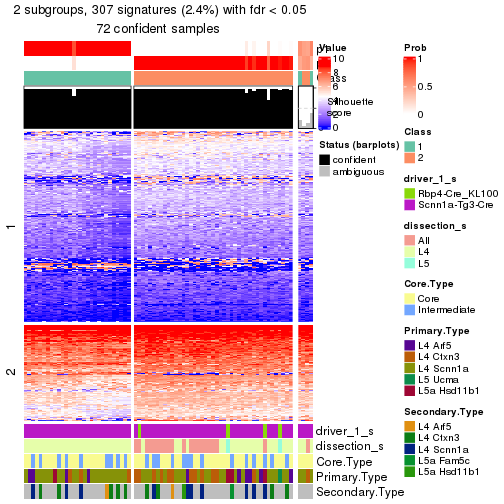
get_signatures(res, k = 3, scale_rows = FALSE)
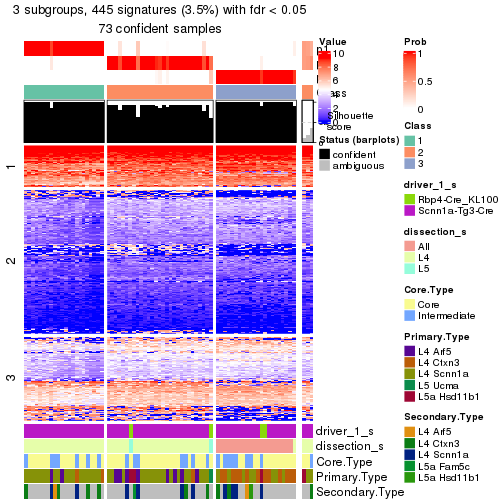
get_signatures(res, k = 4, scale_rows = FALSE)
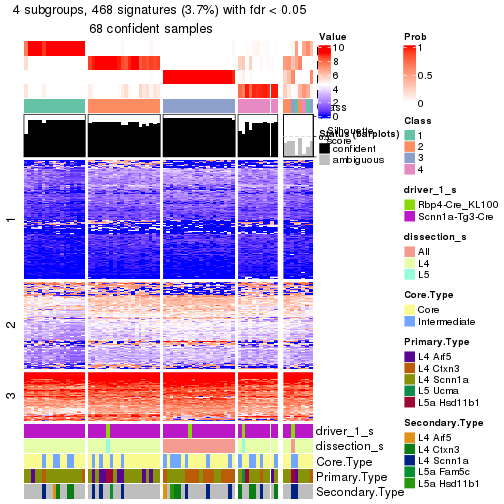
Compare the overlap of signatures from different k:
compare_signatures(res)
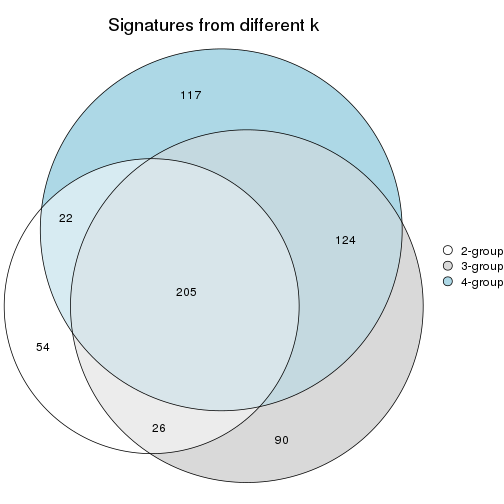
get_signature() returns a data frame invisibly. To get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows (which is done by automatically selecting number of clusters).If there are too many signatures, top_signatures = ... can be set to only show the
signatures with the highest FDRs:
# code only for demonstration
# e.g. to show the top 500 most significant rows
tb = get_signature(res, k = ..., top_signatures = 500)
If the signatures are defined as these which are uniquely high in current group, diff_method argument
can be set to "uniquely_high_in_one_group":
# code only for demonstration
tb = get_signature(res, k = ..., diff_method = "uniquely_high_in_one_group")
UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
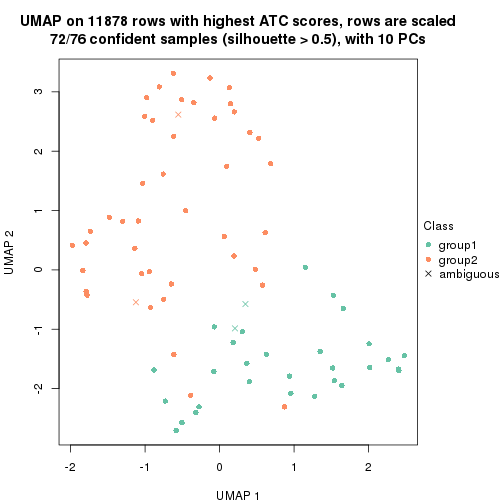
dimension_reduction(res, k = 3, method = "UMAP")
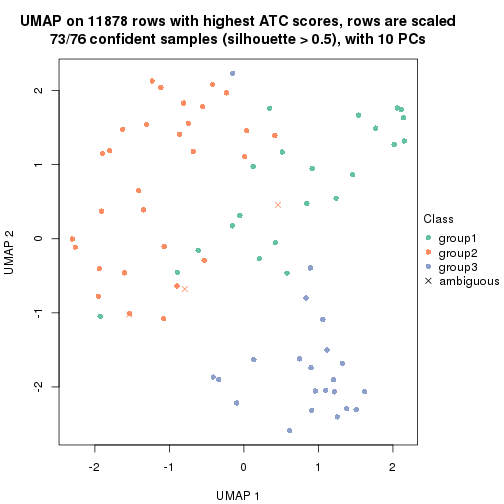
dimension_reduction(res, k = 4, method = "UMAP")
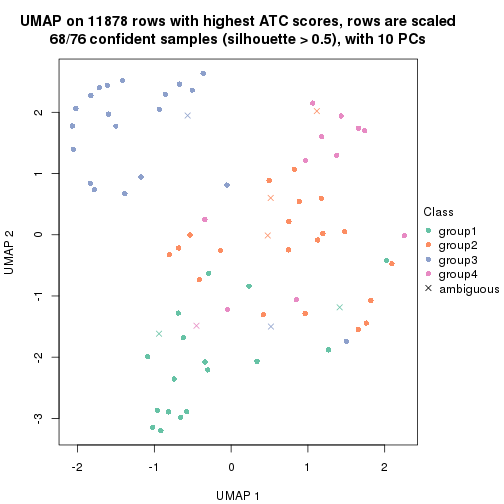
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
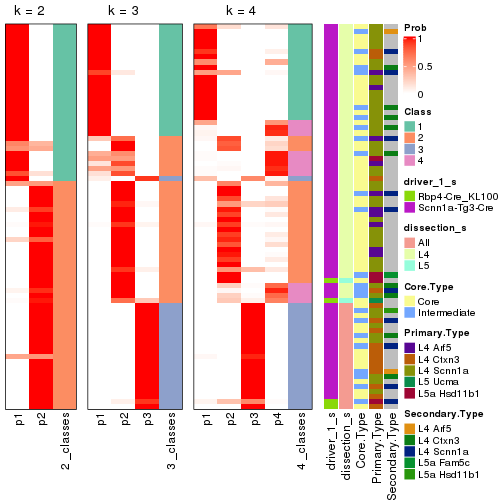
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n_sample driver_1_s(p-value) dissection_s(p-value) Core.Type(p-value)
#> ATC:skmeans 72 0.244 2.29e-05 1.000
#> ATC:skmeans 73 0.379 1.69e-14 0.628
#> ATC:skmeans 68 0.708 4.01e-13 0.497
#> Primary.Type(p-value) Secondary.Type(p-value) k
#> ATC:skmeans 2.60e-01 0.739 2
#> ATC:skmeans 3.57e-05 0.663 3
#> ATC:skmeans 4.14e-05 0.405 4
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
Parent node: Node02. Child nodes: Node0211-leaf , Node0212-leaf , Node0221 , Node0222-leaf .
The object with results only for a single top-value method and a single partitioning method can be extracted as:
res = res_rh["022"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4.
#> On a matrix with 11925 rows and 48 columns.
#> Top rows (1192) are extracted by 'ATC' method.
#> Subgroups are detected by 'skmeans' method.
#> Performed in total 150 partitions by row resampling.
#> Best k for subgroups seems to be 2.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_partitions"
#> [7] "compare_signatures" "consensus_heatmap" "dimension_reduction"
#> [10] "functional_enrichment" "get_anno_col" "get_anno"
#> [13] "get_classes" "get_consensus" "get_matrix"
#> [16] "get_membership" "get_param" "get_signatures"
#> [19] "get_stats" "is_best_k" "is_stable_k"
#> [22] "membership_heatmap" "ncol" "nrow"
#> [25] "plot_ecdf" "predict_classes" "rownames"
#> [28] "select_partition_number" "show" "suggest_best_k"
#> [31] "test_to_known_factors" "top_rows_heatmap"
collect_plots() function collects all the plots made from res for all k (number of subgroups)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
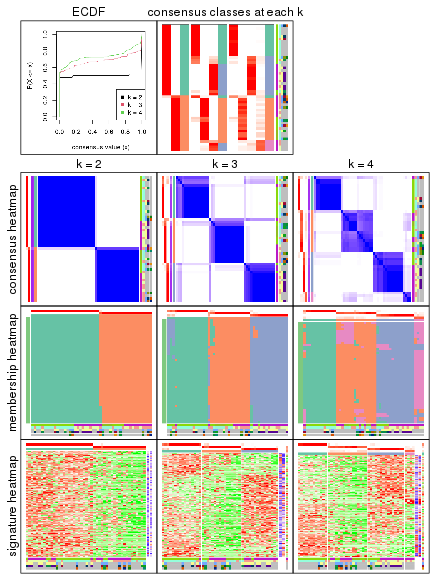
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, higher 1-PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
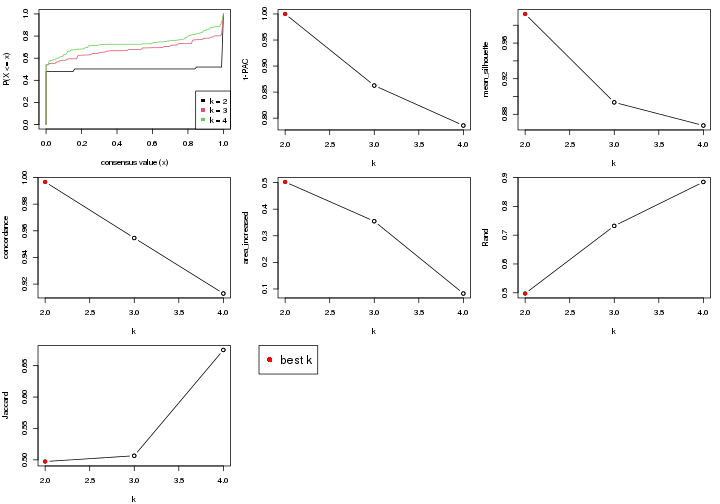
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 1.000 0.993 0.997 0.5022 0.497 0.497
#> 3 3 0.863 0.893 0.955 0.3546 0.732 0.507
#> 4 4 0.786 0.867 0.913 0.0829 0.885 0.675
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 2
Following is the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall subgroup
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> SRR2140055 2 0.000 0.992 0.00 1.00
#> SRR2140083 1 0.000 1.000 1.00 0.00
#> SRR2140046 2 0.000 0.992 0.00 1.00
#> SRR2139988 1 0.000 1.000 1.00 0.00
#> SRR2140079 2 0.000 0.992 0.00 1.00
#> SRR2140041 2 0.000 0.992 0.00 1.00
#> SRR2140084 1 0.000 1.000 1.00 0.00
#> SRR2140080 2 0.000 0.992 0.00 1.00
#> SRR2140077 2 0.000 0.992 0.00 1.00
#> SRR2140063 1 0.000 1.000 1.00 0.00
#> SRR2140016 1 0.000 1.000 1.00 0.00
#> SRR2139997 1 0.000 1.000 1.00 0.00
#> SRR2140085 2 0.000 0.992 0.00 1.00
#> SRR2140078 2 0.000 0.992 0.00 1.00
#> SRR2140047 1 0.000 1.000 1.00 0.00
#> SRR2140054 2 0.634 0.810 0.16 0.84
#> SRR2140082 1 0.000 1.000 1.00 0.00
#> SRR2140086 2 0.000 0.992 0.00 1.00
#> SRR2140062 1 0.000 1.000 1.00 0.00
#> SRR2140076 2 0.000 0.992 0.00 1.00
#> SRR2140018 1 0.000 1.000 1.00 0.00
#> SRR2140081 2 0.000 0.992 0.00 1.00
#> SRR2139847 2 0.000 0.992 0.00 1.00
#> SRR2139802 1 0.000 1.000 1.00 0.00
#> SRR2139751 1 0.000 1.000 1.00 0.00
#> SRR2139854 1 0.000 1.000 1.00 0.00
#> SRR2139770 1 0.000 1.000 1.00 0.00
#> SRR2139853 1 0.000 1.000 1.00 0.00
#> SRR2139721 2 0.000 0.992 0.00 1.00
#> SRR2139844 1 0.000 1.000 1.00 0.00
#> SRR2139801 1 0.000 1.000 1.00 0.00
#> SRR2139704 1 0.000 1.000 1.00 0.00
#> SRR2139850 1 0.000 1.000 1.00 0.00
#> SRR2139843 2 0.000 0.992 0.00 1.00
#> SRR2139849 1 0.000 1.000 1.00 0.00
#> SRR2139852 1 0.000 1.000 1.00 0.00
#> SRR2139855 1 0.000 1.000 1.00 0.00
#> SRR2139698 1 0.000 1.000 1.00 0.00
#> SRR2139846 1 0.000 1.000 1.00 0.00
#> SRR2139729 2 0.000 0.992 0.00 1.00
#> SRR2139842 2 0.000 0.992 0.00 1.00
#> SRR2139851 1 0.000 1.000 1.00 0.00
#> SRR2139813 1 0.000 1.000 1.00 0.00
#> SRR2139845 1 0.000 1.000 1.00 0.00
#> SRR2139333 2 0.000 0.992 0.00 1.00
#> SRR2139383 2 0.000 0.992 0.00 1.00
#> SRR2139384 2 0.000 0.992 0.00 1.00
#> SRR2139325 2 0.000 0.992 0.00 1.00
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> SRR2140055 2 0.0000 0.942 0.00 1.00 0.00
#> SRR2140083 3 0.0000 0.968 0.00 0.00 1.00
#> SRR2140046 2 0.0000 0.942 0.00 1.00 0.00
#> SRR2139988 3 0.0000 0.968 0.00 0.00 1.00
#> SRR2140079 2 0.0000 0.942 0.00 1.00 0.00
#> SRR2140041 2 0.0000 0.942 0.00 1.00 0.00
#> SRR2140084 3 0.0000 0.968 0.00 0.00 1.00
#> SRR2140080 2 0.0000 0.942 0.00 1.00 0.00
#> SRR2140077 3 0.0000 0.968 0.00 0.00 1.00
#> SRR2140063 3 0.0000 0.968 0.00 0.00 1.00
#> SRR2140016 3 0.0000 0.968 0.00 0.00 1.00
#> SRR2139997 3 0.0000 0.968 0.00 0.00 1.00
#> SRR2140085 2 0.0000 0.942 0.00 1.00 0.00
#> SRR2140078 3 0.2537 0.900 0.00 0.08 0.92
#> SRR2140047 3 0.0000 0.968 0.00 0.00 1.00
#> SRR2140054 1 0.2066 0.886 0.94 0.06 0.00
#> SRR2140082 3 0.0000 0.968 0.00 0.00 1.00
#> SRR2140086 2 0.6280 0.113 0.00 0.54 0.46
#> SRR2140062 3 0.0000 0.968 0.00 0.00 1.00
#> SRR2140076 3 0.3340 0.854 0.00 0.12 0.88
#> SRR2140018 3 0.0000 0.968 0.00 0.00 1.00
#> SRR2140081 2 0.0000 0.942 0.00 1.00 0.00
#> SRR2139847 2 0.5216 0.654 0.26 0.74 0.00
#> SRR2139802 1 0.0000 0.938 1.00 0.00 0.00
#> SRR2139751 1 0.4291 0.777 0.82 0.00 0.18
#> SRR2139854 1 0.0000 0.938 1.00 0.00 0.00
#> SRR2139770 3 0.4291 0.754 0.18 0.00 0.82
#> SRR2139853 1 0.0000 0.938 1.00 0.00 0.00
#> SRR2139721 2 0.4291 0.766 0.18 0.82 0.00
#> SRR2139844 1 0.0000 0.938 1.00 0.00 0.00
#> SRR2139801 1 0.0000 0.938 1.00 0.00 0.00
#> SRR2139704 1 0.0000 0.938 1.00 0.00 0.00
#> SRR2139850 1 0.0000 0.938 1.00 0.00 0.00
#> SRR2139843 2 0.0000 0.942 0.00 1.00 0.00
#> SRR2139849 1 0.0000 0.938 1.00 0.00 0.00
#> SRR2139852 1 0.0000 0.938 1.00 0.00 0.00
#> SRR2139855 1 0.0000 0.938 1.00 0.00 0.00
#> SRR2139698 1 0.5560 0.607 0.70 0.00 0.30
#> SRR2139846 1 0.5835 0.530 0.66 0.00 0.34
#> SRR2139729 2 0.0000 0.942 0.00 1.00 0.00
#> SRR2139842 2 0.0000 0.942 0.00 1.00 0.00
#> SRR2139851 1 0.0000 0.938 1.00 0.00 0.00
#> SRR2139813 3 0.0892 0.952 0.02 0.00 0.98
#> SRR2139845 1 0.0000 0.938 1.00 0.00 0.00
#> SRR2139333 2 0.0000 0.942 0.00 1.00 0.00
#> SRR2139383 2 0.0000 0.942 0.00 1.00 0.00
#> SRR2139384 2 0.0000 0.942 0.00 1.00 0.00
#> SRR2139325 2 0.0000 0.942 0.00 1.00 0.00
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> SRR2140055 2 0.2345 0.795 0.00 0.90 0.00 0.10
#> SRR2140083 3 0.0707 0.923 0.00 0.00 0.98 0.02
#> SRR2140046 2 0.0707 0.841 0.00 0.98 0.00 0.02
#> SRR2139988 3 0.0000 0.937 0.00 0.00 1.00 0.00
#> SRR2140079 2 0.3172 0.818 0.00 0.84 0.00 0.16
#> SRR2140041 2 0.0707 0.841 0.00 0.98 0.00 0.02
#> SRR2140084 3 0.0000 0.937 0.00 0.00 1.00 0.00
#> SRR2140080 2 0.2921 0.823 0.00 0.86 0.00 0.14
#> SRR2140077 4 0.3975 0.796 0.00 0.00 0.24 0.76
#> SRR2140063 3 0.0000 0.937 0.00 0.00 1.00 0.00
#> SRR2140016 3 0.0000 0.937 0.00 0.00 1.00 0.00
#> SRR2139997 3 0.0707 0.931 0.00 0.00 0.98 0.02
#> SRR2140085 2 0.1637 0.831 0.00 0.94 0.00 0.06
#> SRR2140078 4 0.4581 0.891 0.00 0.08 0.12 0.80
#> SRR2140047 3 0.0000 0.937 0.00 0.00 1.00 0.00
#> SRR2140054 1 0.6840 0.464 0.60 0.22 0.00 0.18
#> SRR2140082 3 0.0000 0.937 0.00 0.00 1.00 0.00
#> SRR2140086 4 0.4581 0.822 0.00 0.12 0.08 0.80
#> SRR2140062 3 0.0000 0.937 0.00 0.00 1.00 0.00
#> SRR2140076 4 0.4581 0.891 0.00 0.08 0.12 0.80
#> SRR2140018 3 0.0000 0.937 0.00 0.00 1.00 0.00
#> SRR2140081 2 0.3172 0.824 0.00 0.84 0.00 0.16
#> SRR2139847 2 0.5106 0.572 0.24 0.72 0.00 0.04
#> SRR2139802 1 0.0000 0.963 1.00 0.00 0.00 0.00
#> SRR2139751 3 0.4610 0.801 0.10 0.00 0.80 0.10
#> SRR2139854 1 0.0707 0.948 0.98 0.00 0.00 0.02
#> SRR2139770 3 0.3037 0.879 0.02 0.00 0.88 0.10
#> SRR2139853 1 0.0000 0.963 1.00 0.00 0.00 0.00
#> SRR2139721 2 0.4227 0.734 0.06 0.82 0.00 0.12
#> SRR2139844 1 0.0000 0.963 1.00 0.00 0.00 0.00
#> SRR2139801 1 0.0000 0.963 1.00 0.00 0.00 0.00
#> SRR2139704 1 0.0000 0.963 1.00 0.00 0.00 0.00
#> SRR2139850 1 0.0707 0.948 0.98 0.00 0.00 0.02
#> SRR2139843 2 0.3801 0.784 0.00 0.78 0.00 0.22
#> SRR2139849 1 0.0000 0.963 1.00 0.00 0.00 0.00
#> SRR2139852 1 0.0000 0.963 1.00 0.00 0.00 0.00
#> SRR2139855 1 0.0000 0.963 1.00 0.00 0.00 0.00
#> SRR2139698 3 0.3037 0.879 0.02 0.00 0.88 0.10
#> SRR2139846 3 0.4841 0.760 0.14 0.00 0.78 0.08
#> SRR2139729 2 0.2647 0.785 0.00 0.88 0.00 0.12
#> SRR2139842 2 0.3801 0.784 0.00 0.78 0.00 0.22
#> SRR2139851 1 0.0000 0.963 1.00 0.00 0.00 0.00
#> SRR2139813 3 0.2011 0.902 0.00 0.00 0.92 0.08
#> SRR2139845 1 0.0000 0.963 1.00 0.00 0.00 0.00
#> SRR2139333 2 0.0000 0.839 0.00 1.00 0.00 0.00
#> SRR2139383 2 0.3801 0.784 0.00 0.78 0.00 0.22
#> SRR2139384 2 0.3801 0.784 0.00 0.78 0.00 0.22
#> SRR2139325 2 0.0000 0.839 0.00 1.00 0.00 0.00
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
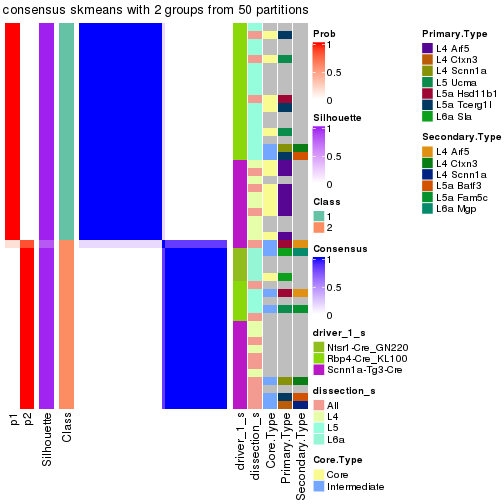
consensus_heatmap(res, k = 3)
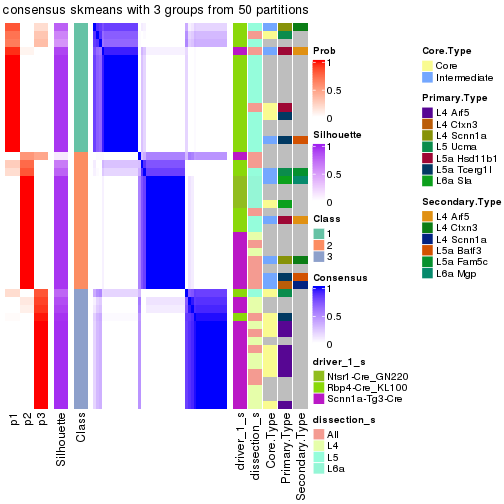
consensus_heatmap(res, k = 4)
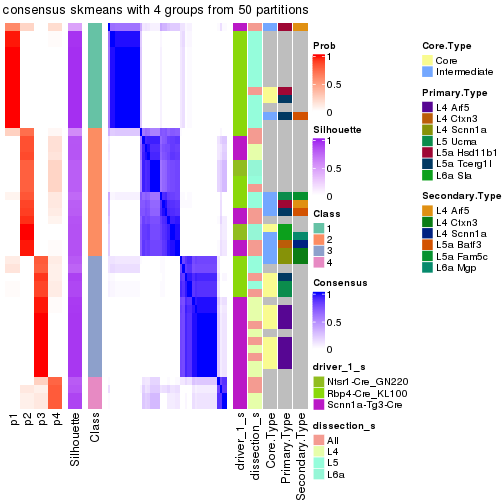
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
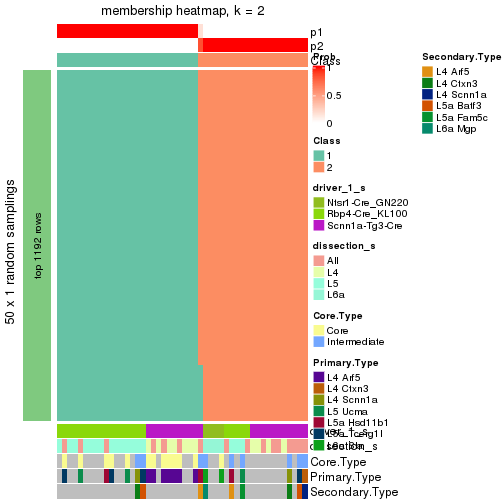
membership_heatmap(res, k = 3)
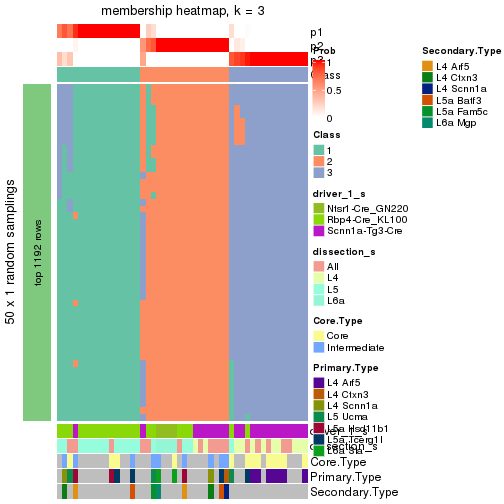
membership_heatmap(res, k = 4)
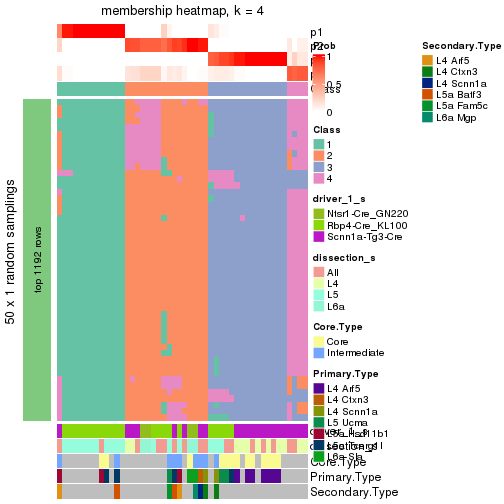
As soon as the classes for columns are determined, the signatures that are significantly different between subgroups can be looked for. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
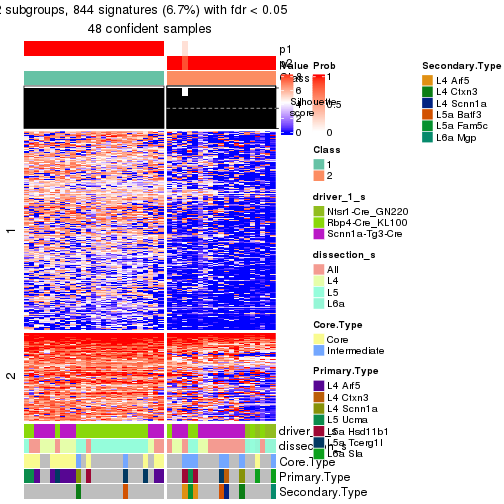
get_signatures(res, k = 3, scale_rows = FALSE)
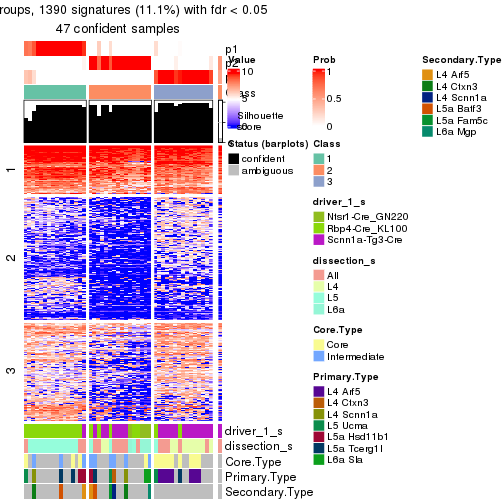
get_signatures(res, k = 4, scale_rows = FALSE)
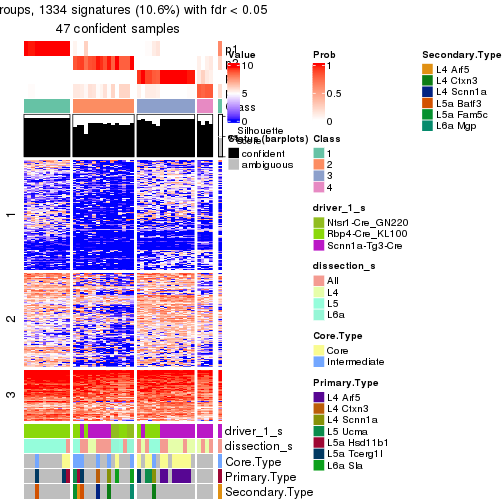
Compare the overlap of signatures from different k:
compare_signatures(res)
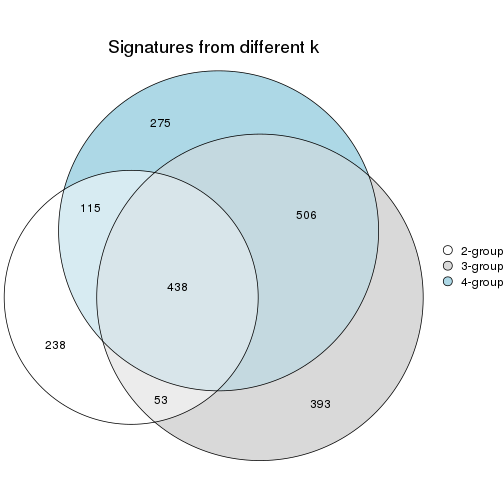
get_signature() returns a data frame invisibly. To get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows (which is done by automatically selecting number of clusters).If there are too many signatures, top_signatures = ... can be set to only show the
signatures with the highest FDRs:
# code only for demonstration
# e.g. to show the top 500 most significant rows
tb = get_signature(res, k = ..., top_signatures = 500)
If the signatures are defined as these which are uniquely high in current group, diff_method argument
can be set to "uniquely_high_in_one_group":
# code only for demonstration
tb = get_signature(res, k = ..., diff_method = "uniquely_high_in_one_group")
UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
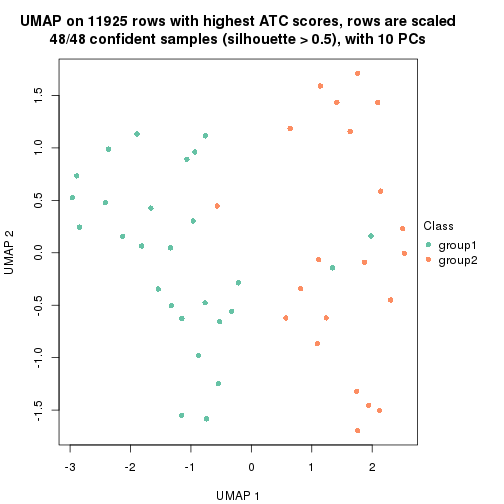
dimension_reduction(res, k = 3, method = "UMAP")
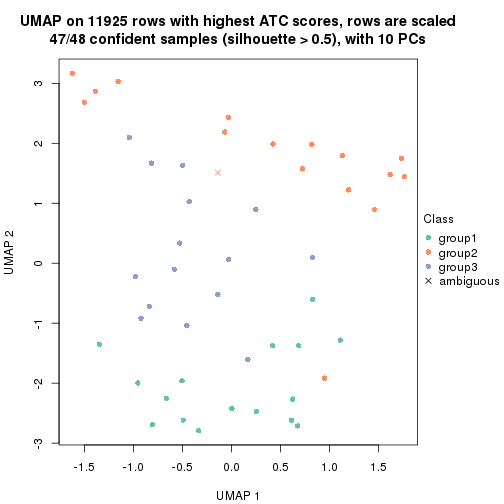
dimension_reduction(res, k = 4, method = "UMAP")
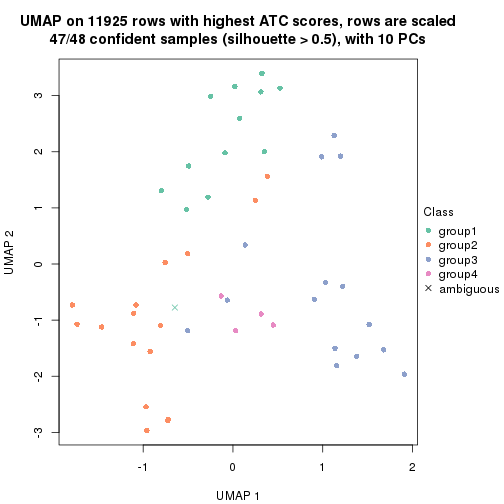
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
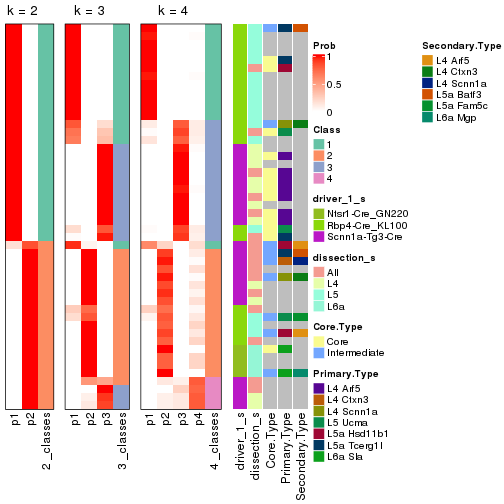
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n_sample driver_1_s(p-value) dissection_s(p-value) Core.Type(p-value)
#> ATC:skmeans 48 6.30e-03 6.19e-03 0.00362
#> ATC:skmeans 47 3.19e-06 2.29e-06 0.00219
#> ATC:skmeans 47 9.35e-05 1.16e-04 0.00479
#> Primary.Type(p-value) Secondary.Type(p-value) k
#> ATC:skmeans 0.0936 0.0333 2
#> ATC:skmeans 0.0372 0.2076 3
#> ATC:skmeans 0.0567 0.2140 4
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
Parent node: Node022. Child nodes: Node02211-leaf , Node02212-leaf , Node02213-leaf .
The object with results only for a single top-value method and a single partitioning method can be extracted as:
res = res_rh["0221"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4.
#> On a matrix with 11864 rows and 27 columns.
#> Top rows (1186) are extracted by 'ATC' method.
#> Subgroups are detected by 'skmeans' method.
#> Performed in total 150 partitions by row resampling.
#> Best k for subgroups seems to be 4.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_partitions"
#> [7] "compare_signatures" "consensus_heatmap" "dimension_reduction"
#> [10] "functional_enrichment" "get_anno_col" "get_anno"
#> [13] "get_classes" "get_consensus" "get_matrix"
#> [16] "get_membership" "get_param" "get_signatures"
#> [19] "get_stats" "is_best_k" "is_stable_k"
#> [22] "membership_heatmap" "ncol" "nrow"
#> [25] "plot_ecdf" "predict_classes" "rownames"
#> [28] "select_partition_number" "show" "suggest_best_k"
#> [31] "test_to_known_factors" "top_rows_heatmap"
collect_plots() function collects all the plots made from res for all k (number of subgroups)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
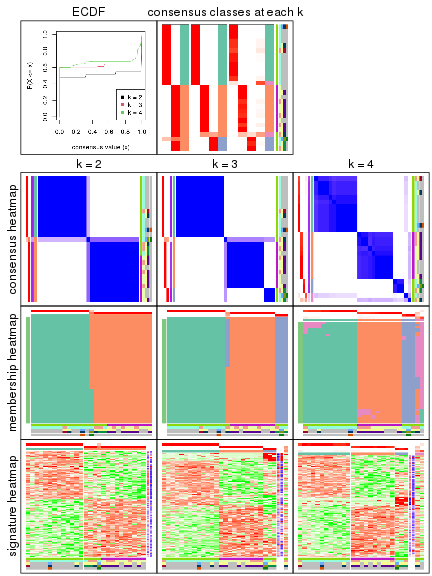
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, higher 1-PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
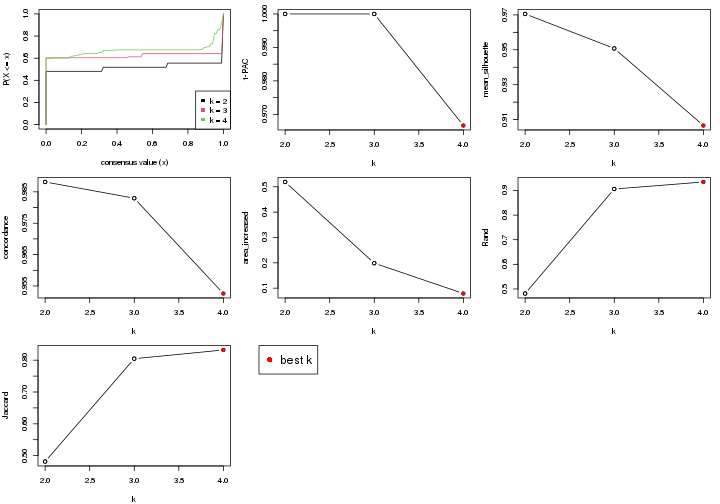
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 1.000 0.971 0.988 0.519 0.481 0.481
#> 3 3 1.000 0.951 0.983 0.199 0.906 0.805
#> 4 4 0.967 0.907 0.953 0.079 0.934 0.832
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 4
#> attr(,"optional")
#> [1] 2 3
There is also optional best \(k\) = 2 3 that is worth to check.
Following is the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall subgroup
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> SRR2140083 2 0.000 0.975 0.00 1.00
#> SRR2139988 2 0.000 0.975 0.00 1.00
#> SRR2140084 2 0.000 0.975 0.00 1.00
#> SRR2140063 2 0.000 0.975 0.00 1.00
#> SRR2140016 2 0.000 0.975 0.00 1.00
#> SRR2139997 2 0.000 0.975 0.00 1.00
#> SRR2140047 2 0.000 0.975 0.00 1.00
#> SRR2140082 2 0.000 0.975 0.00 1.00
#> SRR2140062 2 0.000 0.975 0.00 1.00
#> SRR2140018 2 0.000 0.975 0.00 1.00
#> SRR2139802 1 0.000 1.000 1.00 0.00
#> SRR2139751 2 0.904 0.529 0.32 0.68
#> SRR2139854 1 0.000 1.000 1.00 0.00
#> SRR2139770 2 0.000 0.975 0.00 1.00
#> SRR2139853 1 0.000 1.000 1.00 0.00
#> SRR2139844 1 0.000 1.000 1.00 0.00
#> SRR2139801 1 0.000 1.000 1.00 0.00
#> SRR2139704 1 0.000 1.000 1.00 0.00
#> SRR2139850 1 0.000 1.000 1.00 0.00
#> SRR2139849 1 0.000 1.000 1.00 0.00
#> SRR2139852 1 0.000 1.000 1.00 0.00
#> SRR2139855 1 0.000 1.000 1.00 0.00
#> SRR2139698 2 0.000 0.975 0.00 1.00
#> SRR2139846 1 0.000 1.000 1.00 0.00
#> SRR2139851 1 0.000 1.000 1.00 0.00
#> SRR2139813 2 0.000 0.975 0.00 1.00
#> SRR2139845 1 0.000 1.000 1.00 0.00
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> SRR2140083 2 0.000 0.952 0 1.00 0.00
#> SRR2139988 2 0.000 0.952 0 1.00 0.00
#> SRR2140084 2 0.000 0.952 0 1.00 0.00
#> SRR2140063 2 0.000 0.952 0 1.00 0.00
#> SRR2140016 2 0.000 0.952 0 1.00 0.00
#> SRR2139997 2 0.000 0.952 0 1.00 0.00
#> SRR2140047 2 0.000 0.952 0 1.00 0.00
#> SRR2140082 2 0.000 0.952 0 1.00 0.00
#> SRR2140062 2 0.000 0.952 0 1.00 0.00
#> SRR2140018 2 0.000 0.952 0 1.00 0.00
#> SRR2139802 1 0.000 1.000 1 0.00 0.00
#> SRR2139751 3 0.000 1.000 0 0.00 1.00
#> SRR2139854 1 0.000 1.000 1 0.00 0.00
#> SRR2139770 3 0.000 1.000 0 0.00 1.00
#> SRR2139853 1 0.000 1.000 1 0.00 0.00
#> SRR2139844 1 0.000 1.000 1 0.00 0.00
#> SRR2139801 1 0.000 1.000 1 0.00 0.00
#> SRR2139704 1 0.000 1.000 1 0.00 0.00
#> SRR2139850 1 0.000 1.000 1 0.00 0.00
#> SRR2139849 1 0.000 1.000 1 0.00 0.00
#> SRR2139852 1 0.000 1.000 1 0.00 0.00
#> SRR2139855 1 0.000 1.000 1 0.00 0.00
#> SRR2139698 3 0.000 1.000 0 0.00 1.00
#> SRR2139846 1 0.000 1.000 1 0.00 0.00
#> SRR2139851 1 0.000 1.000 1 0.00 0.00
#> SRR2139813 2 0.628 0.148 0 0.54 0.46
#> SRR2139845 1 0.000 1.000 1 0.00 0.00
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> SRR2140083 2 0.0000 0.969 0.00 1.00 0.00 0.00
#> SRR2139988 2 0.0000 0.969 0.00 1.00 0.00 0.00
#> SRR2140084 2 0.0000 0.969 0.00 1.00 0.00 0.00
#> SRR2140063 2 0.1637 0.947 0.00 0.94 0.00 0.06
#> SRR2140016 2 0.0707 0.964 0.00 0.98 0.00 0.02
#> SRR2139997 2 0.1211 0.944 0.00 0.96 0.00 0.04
#> SRR2140047 2 0.1637 0.947 0.00 0.94 0.00 0.06
#> SRR2140082 2 0.0000 0.969 0.00 1.00 0.00 0.00
#> SRR2140062 2 0.2011 0.936 0.00 0.92 0.00 0.08
#> SRR2140018 2 0.0000 0.969 0.00 1.00 0.00 0.00
#> SRR2139802 1 0.0000 0.969 1.00 0.00 0.00 0.00
#> SRR2139751 3 0.0000 0.978 0.00 0.00 1.00 0.00
#> SRR2139854 1 0.0000 0.969 1.00 0.00 0.00 0.00
#> SRR2139770 3 0.1211 0.954 0.00 0.00 0.96 0.04
#> SRR2139853 1 0.0000 0.969 1.00 0.00 0.00 0.00
#> SRR2139844 1 0.1637 0.949 0.94 0.00 0.00 0.06
#> SRR2139801 1 0.1637 0.949 0.94 0.00 0.00 0.06
#> SRR2139704 1 0.2647 0.896 0.88 0.00 0.00 0.12
#> SRR2139850 1 0.0707 0.958 0.98 0.00 0.00 0.02
#> SRR2139849 1 0.0707 0.965 0.98 0.00 0.00 0.02
#> SRR2139852 1 0.0000 0.969 1.00 0.00 0.00 0.00
#> SRR2139855 1 0.0000 0.969 1.00 0.00 0.00 0.00
#> SRR2139698 3 0.0000 0.978 0.00 0.00 1.00 0.00
#> SRR2139846 4 0.2921 0.278 0.14 0.00 0.00 0.86
#> SRR2139851 1 0.0000 0.969 1.00 0.00 0.00 0.00
#> SRR2139813 4 0.7357 0.229 0.00 0.32 0.18 0.50
#> SRR2139845 1 0.1637 0.949 0.94 0.00 0.00 0.06
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
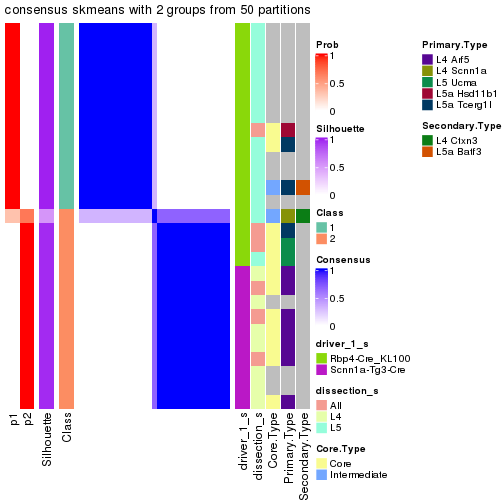
consensus_heatmap(res, k = 3)
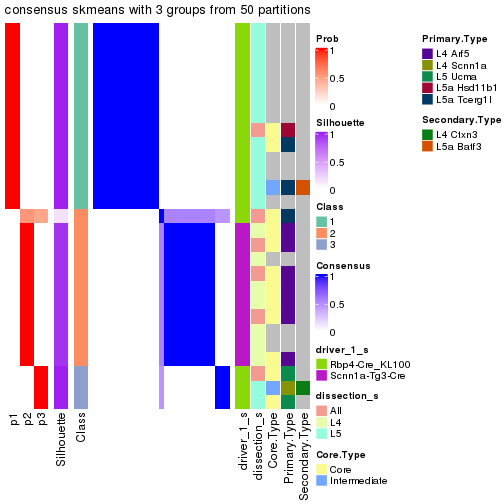
consensus_heatmap(res, k = 4)
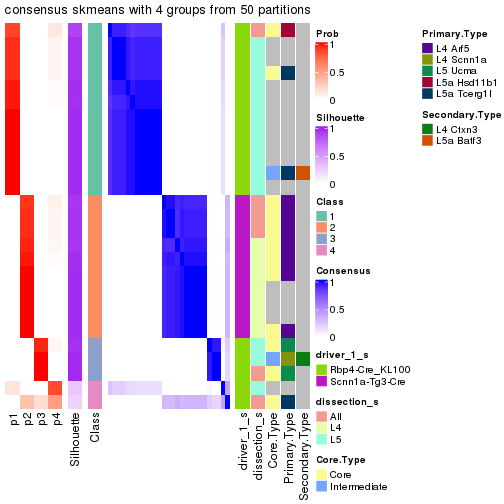
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
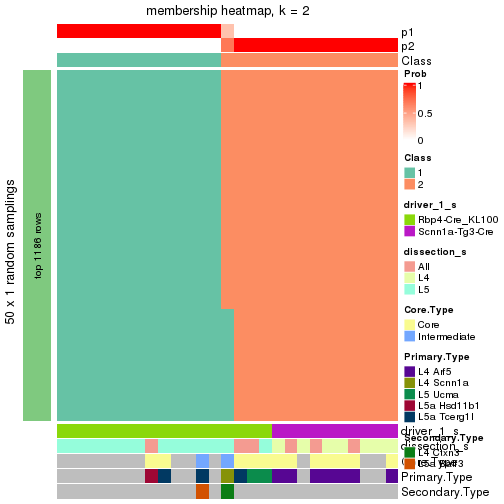
membership_heatmap(res, k = 3)
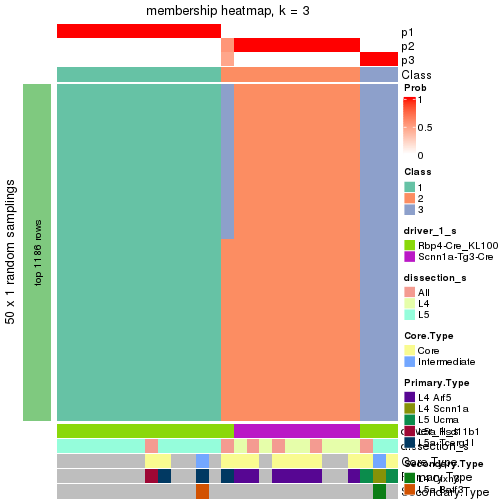
membership_heatmap(res, k = 4)
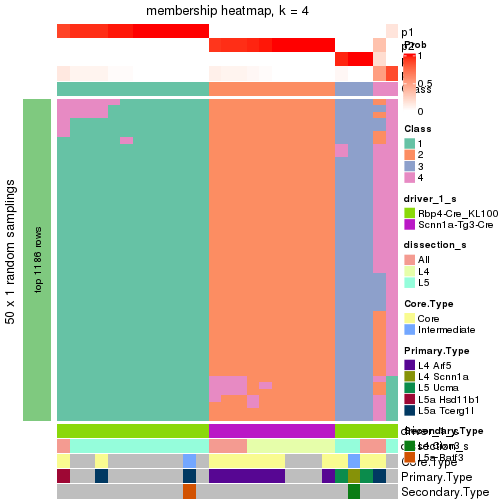
As soon as the classes for columns are determined, the signatures that are significantly different between subgroups can be looked for. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
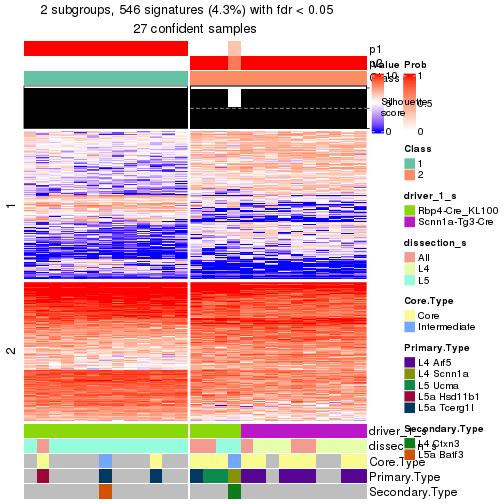
get_signatures(res, k = 3, scale_rows = FALSE)
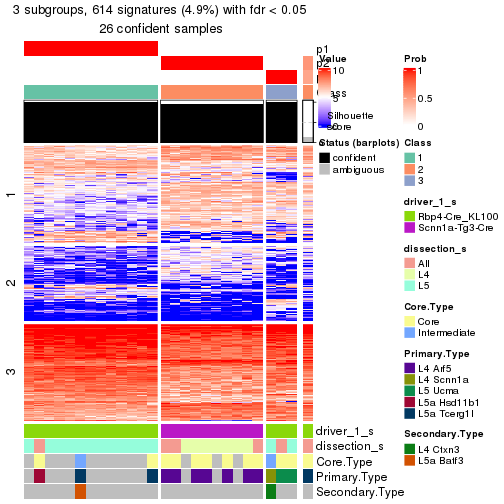
get_signatures(res, k = 4, scale_rows = FALSE)
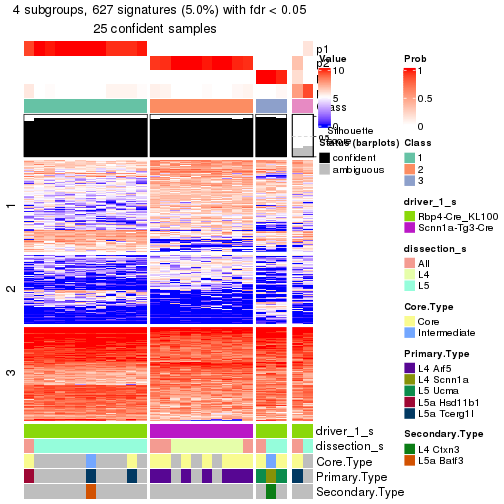
Compare the overlap of signatures from different k:
compare_signatures(res)
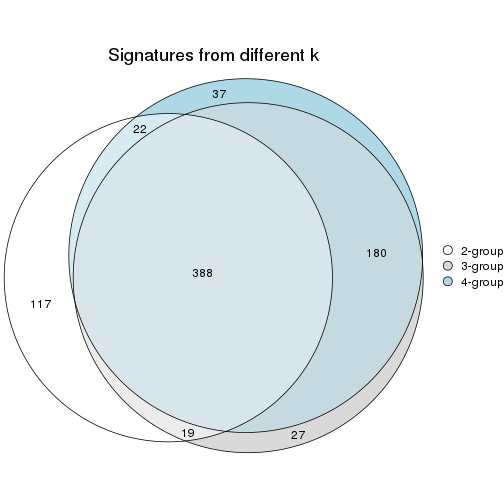
get_signature() returns a data frame invisibly. To get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows (which is done by automatically selecting number of clusters).If there are too many signatures, top_signatures = ... can be set to only show the
signatures with the highest FDRs:
# code only for demonstration
# e.g. to show the top 500 most significant rows
tb = get_signature(res, k = ..., top_signatures = 500)
If the signatures are defined as these which are uniquely high in current group, diff_method argument
can be set to "uniquely_high_in_one_group":
# code only for demonstration
tb = get_signature(res, k = ..., diff_method = "uniquely_high_in_one_group")
UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
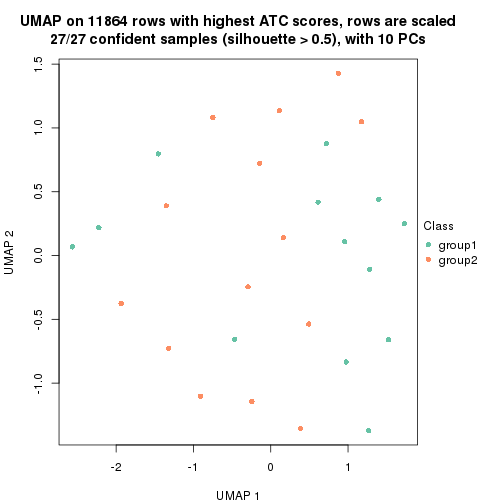
dimension_reduction(res, k = 3, method = "UMAP")
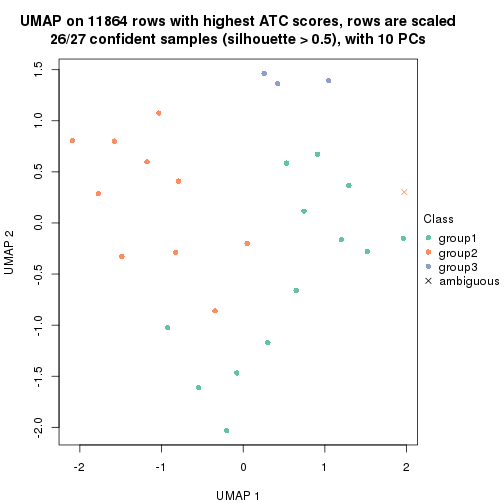
dimension_reduction(res, k = 4, method = "UMAP")
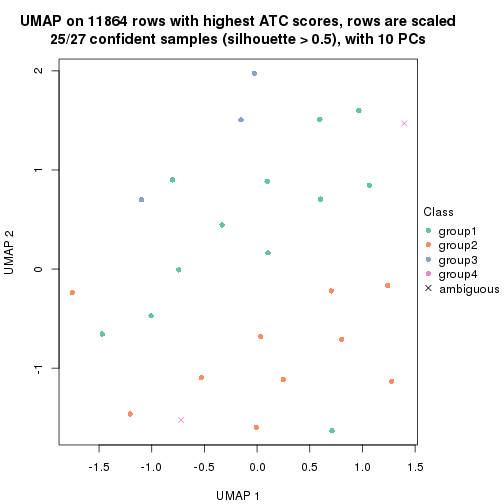
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
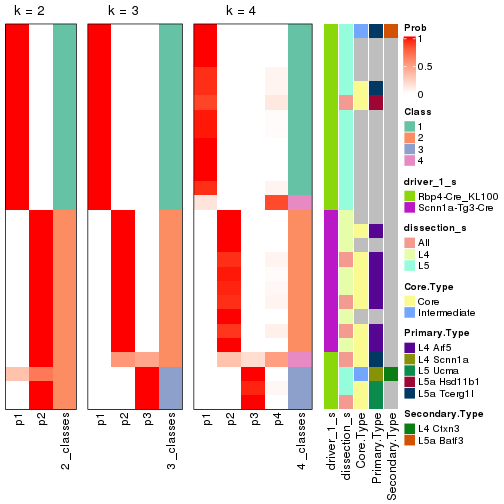
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n_sample driver_1_s(p-value) dissection_s(p-value) Core.Type(p-value)
#> ATC:skmeans 27 5.79e-04 0.000225 0.894
#> ATC:skmeans 26 2.26e-06 0.000195 0.252
#> ATC:skmeans 25 3.73e-06 0.000311 0.252
#> Primary.Type(p-value) Secondary.Type(p-value) k
#> ATC:skmeans 0.03975 0.129 2
#> ATC:skmeans 0.00105 0.131 3
#> ATC:skmeans 0.00105 0.131 4
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
Parent node: Node0. Child nodes: Node011-leaf , Node012-leaf , Node013-leaf , Node021 , Node022 , Node031-leaf , Node032-leaf , Node041-leaf , Node042-leaf .
The object with results only for a single top-value method and a single partitioning method can be extracted as:
res = res_rh["03"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4.
#> On a matrix with 11921 rows and 89 columns.
#> Top rows (1183) are extracted by 'ATC' method.
#> Subgroups are detected by 'skmeans' method.
#> Performed in total 150 partitions by row resampling.
#> Best k for subgroups seems to be 3.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_partitions"
#> [7] "compare_signatures" "consensus_heatmap" "dimension_reduction"
#> [10] "functional_enrichment" "get_anno_col" "get_anno"
#> [13] "get_classes" "get_consensus" "get_matrix"
#> [16] "get_membership" "get_param" "get_signatures"
#> [19] "get_stats" "is_best_k" "is_stable_k"
#> [22] "membership_heatmap" "ncol" "nrow"
#> [25] "plot_ecdf" "predict_classes" "rownames"
#> [28] "select_partition_number" "show" "suggest_best_k"
#> [31] "test_to_known_factors" "top_rows_heatmap"
collect_plots() function collects all the plots made from res for all k (number of subgroups)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
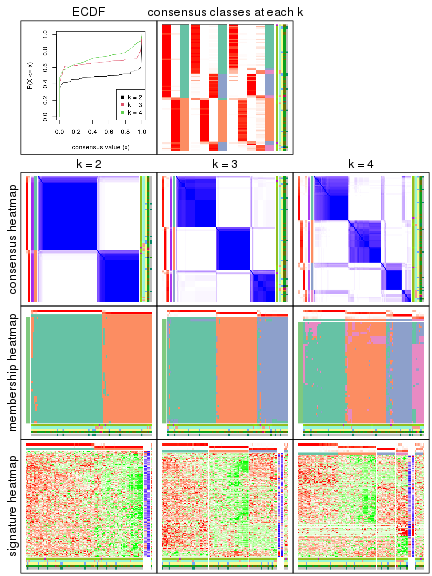
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, higher 1-PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
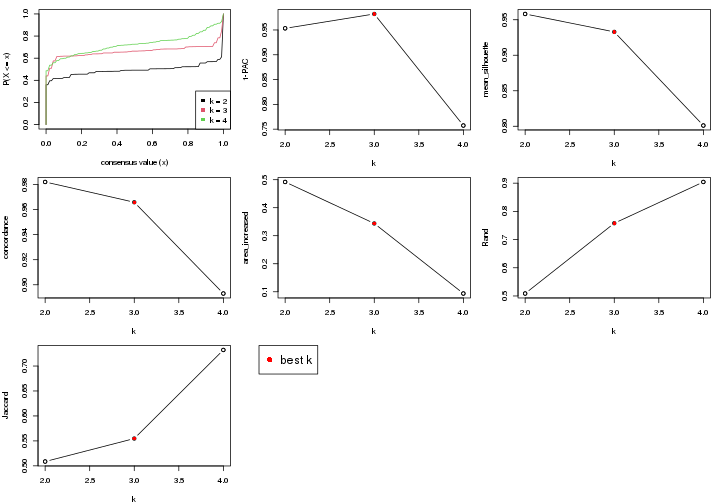
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 0.953 0.958 0.982 0.4919 0.509 0.509
#> 3 3 0.982 0.933 0.966 0.3437 0.758 0.555
#> 4 4 0.757 0.801 0.893 0.0937 0.904 0.732
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 3
#> attr(,"optional")
#> [1] 2
There is also optional best \(k\) = 2 that is worth to check.
Following is the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall subgroup
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> SRR2140038 2 0.584 0.835 0.14 0.86
#> SRR2140037 1 0.000 0.983 1.00 0.00
#> SRR2139829 2 0.000 0.978 0.00 1.00
#> SRR2139690 1 0.000 0.983 1.00 0.00
#> SRR2139767 2 0.000 0.978 0.00 1.00
#> SRR2139789 2 0.141 0.963 0.02 0.98
#> SRR2139757 2 0.000 0.978 0.00 1.00
#> SRR2139712 2 0.000 0.978 0.00 1.00
#> SRR2139825 1 0.000 0.983 1.00 0.00
#> SRR2139828 1 0.000 0.983 1.00 0.00
#> SRR2139831 1 0.000 0.983 1.00 0.00
#> SRR2139766 1 0.000 0.983 1.00 0.00
#> SRR2139791 1 0.981 0.259 0.58 0.42
#> SRR2139708 2 0.795 0.689 0.24 0.76
#> SRR2139306 1 0.000 0.983 1.00 0.00
#> SRR2139371 1 0.000 0.983 1.00 0.00
#> SRR2139343 2 0.000 0.978 0.00 1.00
#> SRR2139334 2 0.855 0.612 0.28 0.72
#> SRR2139349 2 0.000 0.978 0.00 1.00
#> SRR2139368 1 0.000 0.983 1.00 0.00
#> SRR2139315 1 0.000 0.983 1.00 0.00
#> SRR2139362 1 0.000 0.983 1.00 0.00
#> SRR2139350 2 0.000 0.978 0.00 1.00
#> SRR2139327 1 0.000 0.983 1.00 0.00
#> SRR2139320 1 0.000 0.983 1.00 0.00
#> SRR2139357 2 0.242 0.945 0.04 0.96
#> SRR2139318 1 0.000 0.983 1.00 0.00
#> SRR2139381 2 0.000 0.978 0.00 1.00
#> SRR2139365 2 0.000 0.978 0.00 1.00
#> SRR2139312 1 0.469 0.883 0.90 0.10
#> SRR2139344 2 0.000 0.978 0.00 1.00
#> SRR2139339 2 0.000 0.978 0.00 1.00
#> SRR2139376 1 0.000 0.983 1.00 0.00
#> SRR2139378 1 0.000 0.983 1.00 0.00
#> SRR2139372 2 0.000 0.978 0.00 1.00
#> SRR2139337 2 0.000 0.978 0.00 1.00
#> SRR2139340 2 0.000 0.978 0.00 1.00
#> SRR2139361 1 0.000 0.983 1.00 0.00
#> SRR2139316 1 0.000 0.983 1.00 0.00
#> SRR2139324 1 0.000 0.983 1.00 0.00
#> SRR2139353 2 0.000 0.978 0.00 1.00
#> SRR2139359 1 0.000 0.983 1.00 0.00
#> SRR2139354 2 0.000 0.978 0.00 1.00
#> SRR2139323 1 0.000 0.983 1.00 0.00
#> SRR2139329 1 0.242 0.947 0.96 0.04
#> SRR2139311 1 0.000 0.983 1.00 0.00
#> SRR2139366 1 0.000 0.983 1.00 0.00
#> SRR2139382 2 0.000 0.978 0.00 1.00
#> SRR2139347 2 0.000 0.978 0.00 1.00
#> SRR2139330 1 0.000 0.983 1.00 0.00
#> SRR2139308 1 0.000 0.983 1.00 0.00
#> SRR2139375 1 0.000 0.983 1.00 0.00
#> SRR2139338 2 0.000 0.978 0.00 1.00
#> SRR2139345 2 0.000 0.978 0.00 1.00
#> SRR2139332 2 0.000 0.978 0.00 1.00
#> SRR2139377 1 0.000 0.983 1.00 0.00
#> SRR2139356 1 0.000 0.983 1.00 0.00
#> SRR2139321 1 0.000 0.983 1.00 0.00
#> SRR2139313 1 0.000 0.983 1.00 0.00
#> SRR2139364 1 0.000 0.983 1.00 0.00
#> SRR2139319 2 0.141 0.963 0.02 0.98
#> SRR2139380 2 0.000 0.978 0.00 1.00
#> SRR2139363 1 0.000 0.983 1.00 0.00
#> SRR2139314 2 0.141 0.963 0.02 0.98
#> SRR2139369 1 0.000 0.983 1.00 0.00
#> SRR2139326 2 0.000 0.978 0.00 1.00
#> SRR2139351 1 0.000 0.983 1.00 0.00
#> SRR2139370 1 0.000 0.983 1.00 0.00
#> SRR2139307 1 0.000 0.983 1.00 0.00
#> SRR2139348 2 0.000 0.978 0.00 1.00
#> SRR2139335 2 0.000 0.978 0.00 1.00
#> SRR2139342 2 0.000 0.978 0.00 1.00
#> SRR2139331 1 0.584 0.832 0.86 0.14
#> SRR2139346 2 0.000 0.978 0.00 1.00
#> SRR2139374 1 0.000 0.983 1.00 0.00
#> SRR2139309 1 0.584 0.834 0.86 0.14
#> SRR2139328 1 0.000 0.983 1.00 0.00
#> SRR2139322 1 0.000 0.983 1.00 0.00
#> SRR2139355 2 0.000 0.978 0.00 1.00
#> SRR2139367 1 0.000 0.983 1.00 0.00
#> SRR2139310 1 0.000 0.983 1.00 0.00
#> SRR2139317 1 0.000 0.983 1.00 0.00
#> SRR2139360 1 0.000 0.983 1.00 0.00
#> SRR2139358 1 0.000 0.983 1.00 0.00
#> SRR2139352 1 0.000 0.983 1.00 0.00
#> SRR2139373 1 0.000 0.983 1.00 0.00
#> SRR2139379 1 0.000 0.983 1.00 0.00
#> SRR2139341 2 0.000 0.978 0.00 1.00
#> SRR2139336 2 0.000 0.978 0.00 1.00
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> SRR2140038 3 0.7091 0.496 0.04 0.32 0.64
#> SRR2140037 1 0.0892 0.951 0.98 0.00 0.02
#> SRR2139829 3 0.0892 0.923 0.02 0.00 0.98
#> SRR2139690 3 0.0000 0.930 0.00 0.00 1.00
#> SRR2139767 2 0.0000 0.988 0.00 1.00 0.00
#> SRR2139789 3 0.0892 0.923 0.02 0.00 0.98
#> SRR2139757 2 0.0000 0.988 0.00 1.00 0.00
#> SRR2139712 2 0.0000 0.988 0.00 1.00 0.00
#> SRR2139825 1 0.1529 0.940 0.96 0.00 0.04
#> SRR2139828 1 0.1529 0.940 0.96 0.00 0.04
#> SRR2139831 1 0.4555 0.753 0.80 0.00 0.20
#> SRR2139766 1 0.1529 0.940 0.96 0.00 0.04
#> SRR2139791 3 0.0892 0.923 0.02 0.00 0.98
#> SRR2139708 3 0.0000 0.930 0.00 0.00 1.00
#> SRR2139306 1 0.0000 0.963 1.00 0.00 0.00
#> SRR2139371 1 0.0892 0.968 0.98 0.00 0.02
#> SRR2139343 2 0.0000 0.988 0.00 1.00 0.00
#> SRR2139334 1 0.6045 0.378 0.62 0.38 0.00
#> SRR2139349 2 0.0000 0.988 0.00 1.00 0.00
#> SRR2139368 1 0.0892 0.968 0.98 0.00 0.02
#> SRR2139315 3 0.1529 0.928 0.04 0.00 0.96
#> SRR2139362 1 0.0892 0.968 0.98 0.00 0.02
#> SRR2139350 2 0.0000 0.988 0.00 1.00 0.00
#> SRR2139327 3 0.5016 0.689 0.24 0.00 0.76
#> SRR2139320 3 0.0892 0.936 0.02 0.00 0.98
#> SRR2139357 2 0.2066 0.923 0.06 0.94 0.00
#> SRR2139318 3 0.0892 0.936 0.02 0.00 0.98
#> SRR2139381 2 0.0000 0.988 0.00 1.00 0.00
#> SRR2139365 2 0.0000 0.988 0.00 1.00 0.00
#> SRR2139312 1 0.0000 0.963 1.00 0.00 0.00
#> SRR2139344 2 0.0000 0.988 0.00 1.00 0.00
#> SRR2139339 2 0.1529 0.951 0.04 0.96 0.00
#> SRR2139376 1 0.0892 0.968 0.98 0.00 0.02
#> SRR2139378 3 0.6280 0.171 0.46 0.00 0.54
#> SRR2139372 2 0.0000 0.988 0.00 1.00 0.00
#> SRR2139337 2 0.0000 0.988 0.00 1.00 0.00
#> SRR2139340 2 0.0000 0.988 0.00 1.00 0.00
#> SRR2139361 1 0.0892 0.968 0.98 0.00 0.02
#> SRR2139316 3 0.0892 0.936 0.02 0.00 0.98
#> SRR2139324 3 0.1529 0.928 0.04 0.00 0.96
#> SRR2139353 2 0.0000 0.988 0.00 1.00 0.00
#> SRR2139359 1 0.0892 0.968 0.98 0.00 0.02
#> SRR2139354 2 0.0000 0.988 0.00 1.00 0.00
#> SRR2139323 3 0.0892 0.936 0.02 0.00 0.98
#> SRR2139329 3 0.0892 0.936 0.02 0.00 0.98
#> SRR2139311 1 0.0000 0.963 1.00 0.00 0.00
#> SRR2139366 1 0.0892 0.968 0.98 0.00 0.02
#> SRR2139382 2 0.0000 0.988 0.00 1.00 0.00
#> SRR2139347 2 0.0000 0.988 0.00 1.00 0.00
#> SRR2139330 3 0.1529 0.928 0.04 0.00 0.96
#> SRR2139308 1 0.0000 0.963 1.00 0.00 0.00
#> SRR2139375 1 0.0892 0.968 0.98 0.00 0.02
#> SRR2139338 2 0.0000 0.988 0.00 1.00 0.00
#> SRR2139345 2 0.0000 0.988 0.00 1.00 0.00
#> SRR2139332 2 0.0000 0.988 0.00 1.00 0.00
#> SRR2139377 1 0.0892 0.968 0.98 0.00 0.02
#> SRR2139356 1 0.0892 0.968 0.98 0.00 0.02
#> SRR2139321 3 0.0892 0.936 0.02 0.00 0.98
#> SRR2139313 1 0.0000 0.963 1.00 0.00 0.00
#> SRR2139364 1 0.0892 0.968 0.98 0.00 0.02
#> SRR2139319 3 0.0892 0.923 0.02 0.00 0.98
#> SRR2139380 2 0.0000 0.988 0.00 1.00 0.00
#> SRR2139363 1 0.0892 0.968 0.98 0.00 0.02
#> SRR2139314 3 0.2066 0.894 0.00 0.06 0.94
#> SRR2139369 1 0.0892 0.968 0.98 0.00 0.02
#> SRR2139326 2 0.4796 0.709 0.00 0.78 0.22
#> SRR2139351 1 0.0000 0.963 1.00 0.00 0.00
#> SRR2139370 1 0.0892 0.954 0.98 0.00 0.02
#> SRR2139307 1 0.0000 0.963 1.00 0.00 0.00
#> SRR2139348 2 0.0000 0.988 0.00 1.00 0.00
#> SRR2139335 2 0.0000 0.988 0.00 1.00 0.00
#> SRR2139342 2 0.0000 0.988 0.00 1.00 0.00
#> SRR2139331 3 0.0000 0.930 0.00 0.00 1.00
#> SRR2139346 2 0.0000 0.988 0.00 1.00 0.00
#> SRR2139374 1 0.0892 0.968 0.98 0.00 0.02
#> SRR2139309 1 0.0892 0.952 0.98 0.02 0.00
#> SRR2139328 3 0.1529 0.928 0.04 0.00 0.96
#> SRR2139322 3 0.0892 0.936 0.02 0.00 0.98
#> SRR2139355 2 0.0000 0.988 0.00 1.00 0.00
#> SRR2139367 1 0.0892 0.968 0.98 0.00 0.02
#> SRR2139310 1 0.0000 0.963 1.00 0.00 0.00
#> SRR2139317 3 0.0892 0.936 0.02 0.00 0.98
#> SRR2139360 1 0.0892 0.968 0.98 0.00 0.02
#> SRR2139358 1 0.2066 0.935 0.94 0.00 0.06
#> SRR2139352 1 0.0892 0.968 0.98 0.00 0.02
#> SRR2139373 1 0.0892 0.968 0.98 0.00 0.02
#> SRR2139379 1 0.0892 0.968 0.98 0.00 0.02
#> SRR2139341 2 0.0000 0.988 0.00 1.00 0.00
#> SRR2139336 2 0.0000 0.988 0.00 1.00 0.00
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> SRR2140038 3 0.8335 0.3311 0.12 0.20 0.56 0.12
#> SRR2140037 1 0.0000 0.9253 1.00 0.00 0.00 0.00
#> SRR2139829 4 0.3972 0.7056 0.00 0.08 0.08 0.84
#> SRR2139690 4 0.4797 0.6575 0.02 0.00 0.26 0.72
#> SRR2139767 2 0.3172 0.8413 0.00 0.84 0.00 0.16
#> SRR2139789 4 0.3606 0.7356 0.00 0.02 0.14 0.84
#> SRR2139757 2 0.1637 0.8990 0.00 0.94 0.00 0.06
#> SRR2139712 2 0.3610 0.8039 0.00 0.80 0.00 0.20
#> SRR2139825 4 0.4790 0.5078 0.38 0.00 0.00 0.62
#> SRR2139828 4 0.4713 0.5460 0.36 0.00 0.00 0.64
#> SRR2139831 4 0.5173 0.6055 0.32 0.00 0.02 0.66
#> SRR2139766 1 0.4790 0.2195 0.62 0.00 0.00 0.38
#> SRR2139791 4 0.3172 0.7378 0.00 0.00 0.16 0.84
#> SRR2139708 4 0.4134 0.6632 0.00 0.00 0.26 0.74
#> SRR2139306 1 0.2011 0.8913 0.92 0.00 0.00 0.08
#> SRR2139371 1 0.0000 0.9253 1.00 0.00 0.00 0.00
#> SRR2139343 2 0.1637 0.8952 0.00 0.94 0.00 0.06
#> SRR2139334 2 0.7855 -0.0376 0.30 0.40 0.00 0.30
#> SRR2139349 2 0.2011 0.8997 0.00 0.92 0.00 0.08
#> SRR2139368 1 0.0000 0.9253 1.00 0.00 0.00 0.00
#> SRR2139315 3 0.0000 0.8304 0.00 0.00 1.00 0.00
#> SRR2139362 1 0.0000 0.9253 1.00 0.00 0.00 0.00
#> SRR2139350 2 0.1637 0.9002 0.00 0.94 0.00 0.06
#> SRR2139327 3 0.5271 0.3803 0.34 0.00 0.64 0.02
#> SRR2139320 3 0.0000 0.8304 0.00 0.00 1.00 0.00
#> SRR2139357 2 0.3935 0.8380 0.00 0.84 0.06 0.10
#> SRR2139318 3 0.0000 0.8304 0.00 0.00 1.00 0.00
#> SRR2139381 2 0.2647 0.8392 0.00 0.88 0.00 0.12
#> SRR2139365 2 0.0707 0.8954 0.00 0.98 0.00 0.02
#> SRR2139312 1 0.4088 0.8211 0.82 0.04 0.00 0.14
#> SRR2139344 2 0.2011 0.8997 0.00 0.92 0.00 0.08
#> SRR2139339 2 0.4797 0.6727 0.02 0.72 0.00 0.26
#> SRR2139376 1 0.0000 0.9253 1.00 0.00 0.00 0.00
#> SRR2139378 3 0.4855 0.3248 0.40 0.00 0.60 0.00
#> SRR2139372 2 0.0707 0.8954 0.00 0.98 0.00 0.02
#> SRR2139337 2 0.1913 0.8828 0.00 0.94 0.02 0.04
#> SRR2139340 2 0.2011 0.8997 0.00 0.92 0.00 0.08
#> SRR2139361 1 0.0000 0.9253 1.00 0.00 0.00 0.00
#> SRR2139316 3 0.0000 0.8304 0.00 0.00 1.00 0.00
#> SRR2139324 3 0.0000 0.8304 0.00 0.00 1.00 0.00
#> SRR2139353 2 0.2011 0.8997 0.00 0.92 0.00 0.08
#> SRR2139359 1 0.0000 0.9253 1.00 0.00 0.00 0.00
#> SRR2139354 2 0.2011 0.8997 0.00 0.92 0.00 0.08
#> SRR2139323 3 0.0000 0.8304 0.00 0.00 1.00 0.00
#> SRR2139329 3 0.0000 0.8304 0.00 0.00 1.00 0.00
#> SRR2139311 1 0.5422 0.7352 0.74 0.04 0.02 0.20
#> SRR2139366 1 0.0000 0.9253 1.00 0.00 0.00 0.00
#> SRR2139382 2 0.1211 0.8893 0.00 0.96 0.00 0.04
#> SRR2139347 2 0.2011 0.8997 0.00 0.92 0.00 0.08
#> SRR2139330 3 0.0000 0.8304 0.00 0.00 1.00 0.00
#> SRR2139308 1 0.4332 0.7974 0.80 0.04 0.00 0.16
#> SRR2139375 1 0.0000 0.9253 1.00 0.00 0.00 0.00
#> SRR2139338 2 0.1211 0.8901 0.00 0.96 0.00 0.04
#> SRR2139345 2 0.2011 0.8997 0.00 0.92 0.00 0.08
#> SRR2139332 2 0.0000 0.8980 0.00 1.00 0.00 0.00
#> SRR2139377 1 0.0000 0.9253 1.00 0.00 0.00 0.00
#> SRR2139356 1 0.2345 0.8802 0.90 0.00 0.00 0.10
#> SRR2139321 3 0.0000 0.8304 0.00 0.00 1.00 0.00
#> SRR2139313 1 0.2921 0.8584 0.86 0.00 0.00 0.14
#> SRR2139364 1 0.0000 0.9253 1.00 0.00 0.00 0.00
#> SRR2139319 4 0.3172 0.7378 0.00 0.00 0.16 0.84
#> SRR2139380 2 0.3801 0.8008 0.00 0.78 0.00 0.22
#> SRR2139363 1 0.0000 0.9253 1.00 0.00 0.00 0.00
#> SRR2139314 3 0.0000 0.8304 0.00 0.00 1.00 0.00
#> SRR2139369 1 0.0000 0.9253 1.00 0.00 0.00 0.00
#> SRR2139326 3 0.6150 0.2976 0.00 0.36 0.58 0.06
#> SRR2139351 1 0.1637 0.9018 0.94 0.00 0.00 0.06
#> SRR2139370 1 0.1913 0.9035 0.94 0.02 0.00 0.04
#> SRR2139307 1 0.3606 0.8326 0.84 0.02 0.00 0.14
#> SRR2139348 2 0.2011 0.8997 0.00 0.92 0.00 0.08
#> SRR2139335 2 0.0707 0.8954 0.00 0.98 0.00 0.02
#> SRR2139342 2 0.2647 0.8392 0.00 0.88 0.00 0.12
#> SRR2139331 3 0.0707 0.8132 0.00 0.00 0.98 0.02
#> SRR2139346 2 0.2011 0.8997 0.00 0.92 0.00 0.08
#> SRR2139374 1 0.0000 0.9253 1.00 0.00 0.00 0.00
#> SRR2139309 1 0.4491 0.7894 0.80 0.06 0.00 0.14
#> SRR2139328 3 0.0000 0.8304 0.00 0.00 1.00 0.00
#> SRR2139322 3 0.0000 0.8304 0.00 0.00 1.00 0.00
#> SRR2139355 2 0.2011 0.8997 0.00 0.92 0.00 0.08
#> SRR2139367 1 0.0000 0.9253 1.00 0.00 0.00 0.00
#> SRR2139310 1 0.0707 0.9180 0.98 0.00 0.00 0.02
#> SRR2139317 3 0.0000 0.8304 0.00 0.00 1.00 0.00
#> SRR2139360 1 0.0000 0.9253 1.00 0.00 0.00 0.00
#> SRR2139358 3 0.4994 0.1372 0.48 0.00 0.52 0.00
#> SRR2139352 1 0.4211 0.8228 0.84 0.02 0.04 0.10
#> SRR2139373 1 0.0000 0.9253 1.00 0.00 0.00 0.00
#> SRR2139379 1 0.1211 0.8959 0.96 0.00 0.04 0.00
#> SRR2139341 2 0.1211 0.8893 0.00 0.96 0.00 0.04
#> SRR2139336 2 0.0707 0.8954 0.00 0.98 0.00 0.02
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
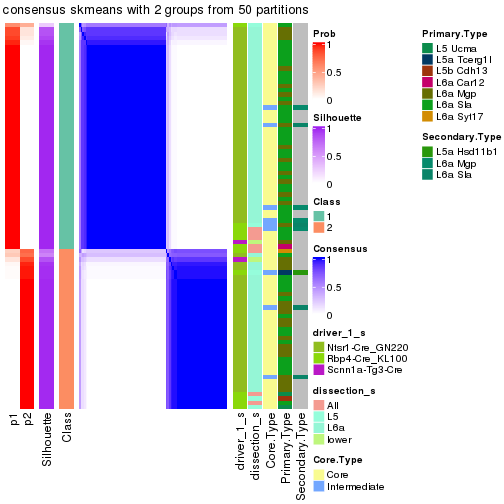
consensus_heatmap(res, k = 3)
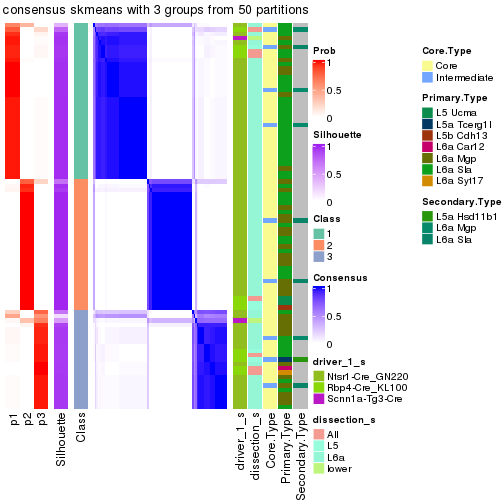
consensus_heatmap(res, k = 4)
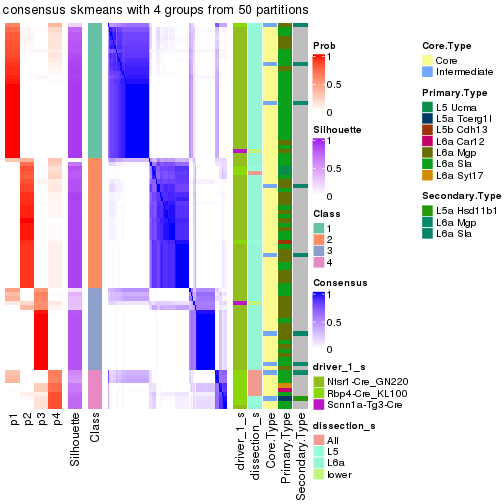
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
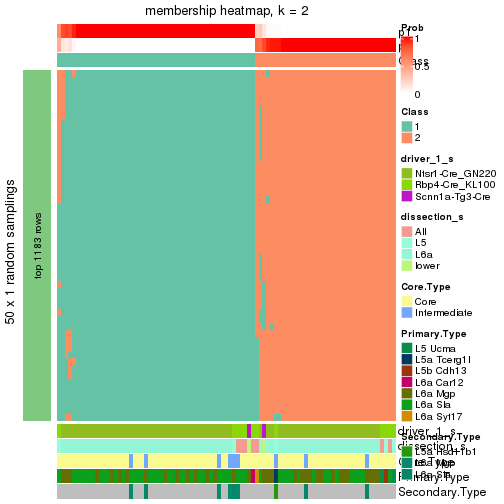
membership_heatmap(res, k = 3)
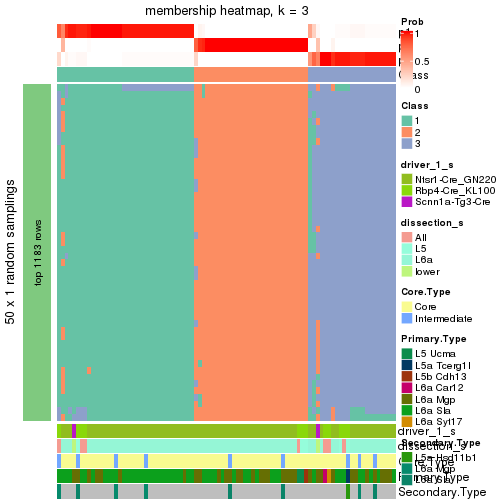
membership_heatmap(res, k = 4)
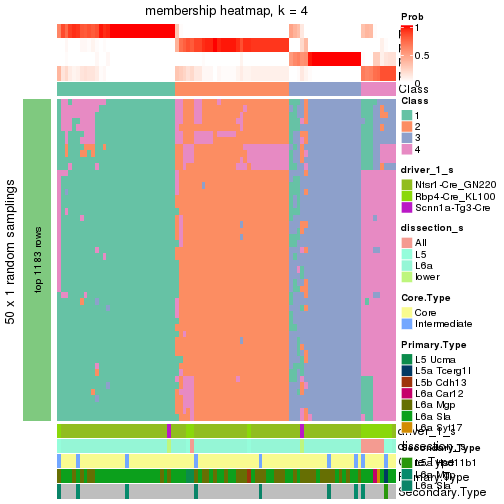
As soon as the classes for columns are determined, the signatures that are significantly different between subgroups can be looked for. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
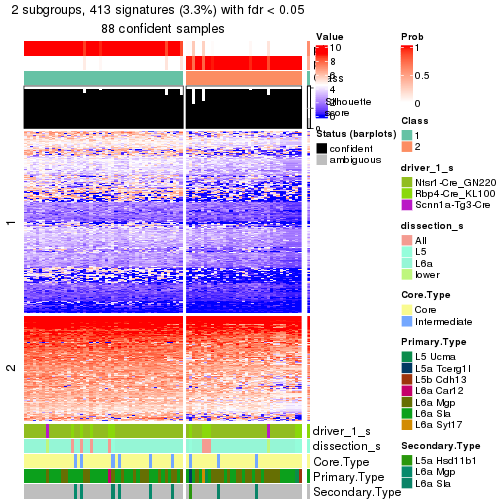
get_signatures(res, k = 3, scale_rows = FALSE)
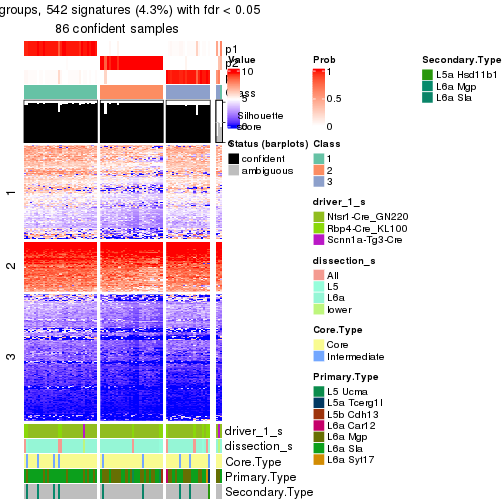
get_signatures(res, k = 4, scale_rows = FALSE)
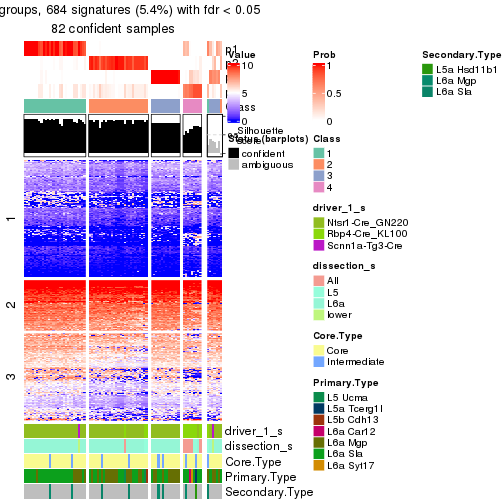
Compare the overlap of signatures from different k:
compare_signatures(res)
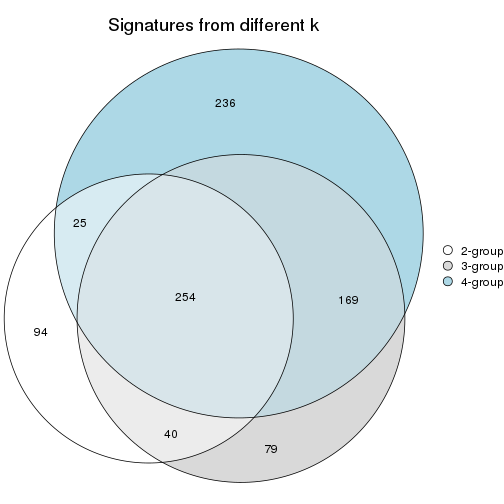
get_signature() returns a data frame invisibly. To get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows (which is done by automatically selecting number of clusters).If there are too many signatures, top_signatures = ... can be set to only show the
signatures with the highest FDRs:
# code only for demonstration
# e.g. to show the top 500 most significant rows
tb = get_signature(res, k = ..., top_signatures = 500)
If the signatures are defined as these which are uniquely high in current group, diff_method argument
can be set to "uniquely_high_in_one_group":
# code only for demonstration
tb = get_signature(res, k = ..., diff_method = "uniquely_high_in_one_group")
UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
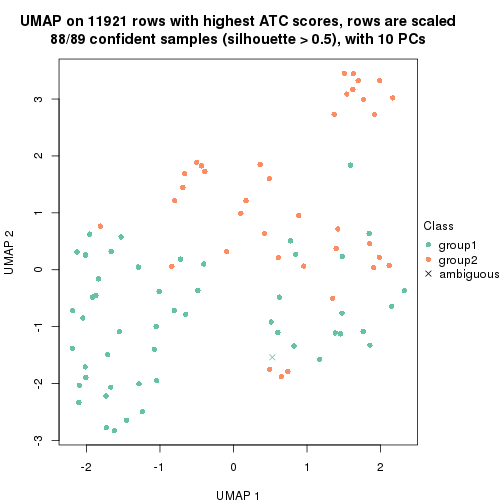
dimension_reduction(res, k = 3, method = "UMAP")
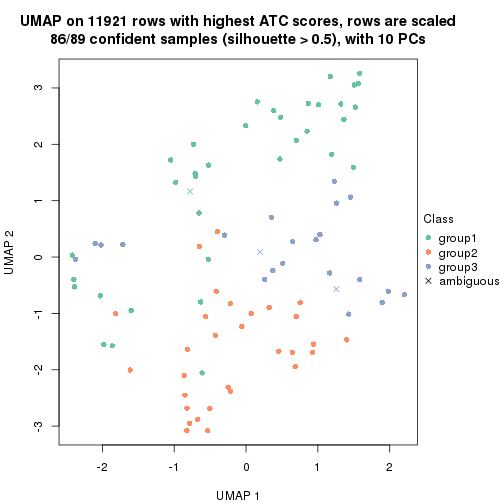
dimension_reduction(res, k = 4, method = "UMAP")
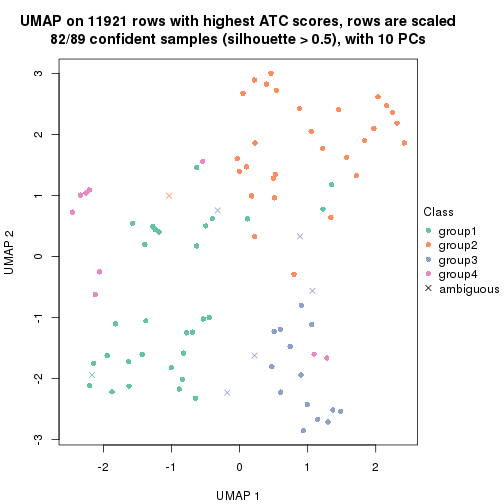
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
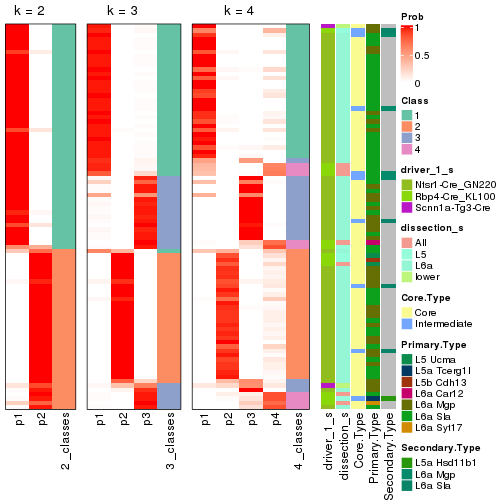
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n_sample driver_1_s(p-value) dissection_s(p-value) Core.Type(p-value)
#> ATC:skmeans 88 6.42e-01 5.80e-01 0.840
#> ATC:skmeans 86 4.49e-01 5.91e-01 0.662
#> ATC:skmeans 82 1.33e-09 6.00e-09 0.474
#> Primary.Type(p-value) Secondary.Type(p-value) k
#> ATC:skmeans 0.075147 0.220 2
#> ATC:skmeans 0.015875 0.397 3
#> ATC:skmeans 0.000424 0.139 4
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
Parent node: Node0. Child nodes: Node011-leaf , Node012-leaf , Node013-leaf , Node021 , Node022 , Node031-leaf , Node032-leaf , Node041-leaf , Node042-leaf .
The object with results only for a single top-value method and a single partitioning method can be extracted as:
res = res_rh["04"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4.
#> On a matrix with 11934 rows and 73 columns.
#> Top rows (883) are extracted by 'ATC' method.
#> Subgroups are detected by 'skmeans' method.
#> Performed in total 150 partitions by row resampling.
#> Best k for subgroups seems to be 2.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_partitions"
#> [7] "compare_signatures" "consensus_heatmap" "dimension_reduction"
#> [10] "functional_enrichment" "get_anno_col" "get_anno"
#> [13] "get_classes" "get_consensus" "get_matrix"
#> [16] "get_membership" "get_param" "get_signatures"
#> [19] "get_stats" "is_best_k" "is_stable_k"
#> [22] "membership_heatmap" "ncol" "nrow"
#> [25] "plot_ecdf" "predict_classes" "rownames"
#> [28] "select_partition_number" "show" "suggest_best_k"
#> [31] "test_to_known_factors" "top_rows_heatmap"
collect_plots() function collects all the plots made from res for all k (number of subgroups)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
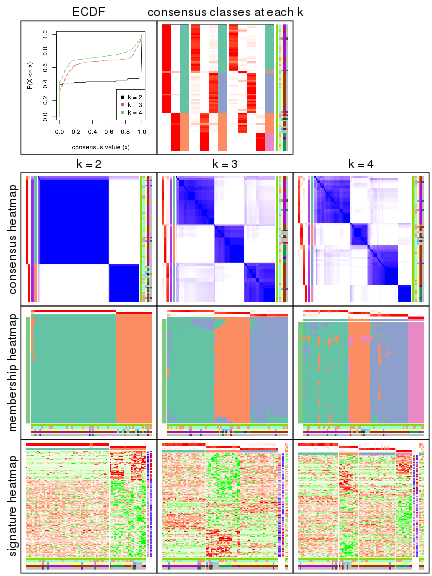
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, higher 1-PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
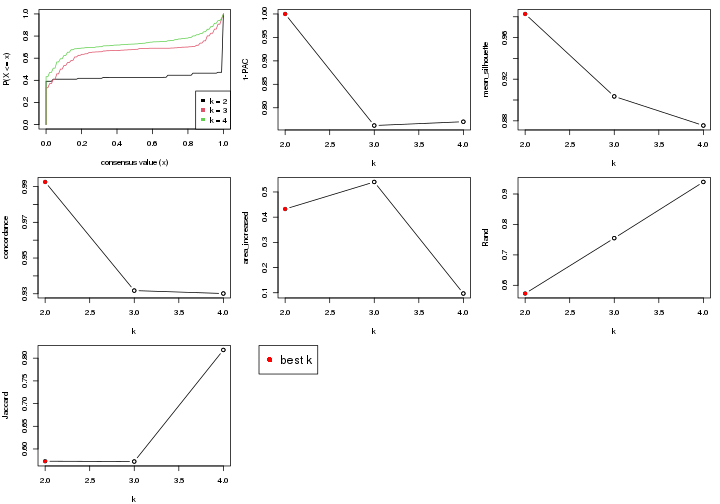
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 1.000 0.983 0.993 0.4323 0.573 0.573
#> 3 3 0.762 0.903 0.932 0.5397 0.755 0.572
#> 4 4 0.770 0.875 0.930 0.0969 0.939 0.818
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 2
Following is the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall subgroup
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> SRR2139787 1 0.000 0.990 1.00 0.00
#> SRR2139769 1 0.000 0.990 1.00 0.00
#> SRR2139680 2 0.000 0.998 0.00 1.00
#> SRR2139714 2 0.000 0.998 0.00 1.00
#> SRR2139763 1 0.000 0.990 1.00 0.00
#> SRR2139808 1 0.000 0.990 1.00 0.00
#> SRR2139707 1 0.000 0.990 1.00 0.00
#> SRR2139699 2 0.000 0.998 0.00 1.00
#> SRR2139677 2 0.000 0.998 0.00 1.00
#> SRR2139794 2 0.000 0.998 0.00 1.00
#> SRR2139742 1 0.000 0.990 1.00 0.00
#> SRR2139748 1 0.000 0.990 1.00 0.00
#> SRR2139732 1 0.000 0.990 1.00 0.00
#> SRR2139745 1 0.000 0.990 1.00 0.00
#> SRR2139738 1 0.000 0.990 1.00 0.00
#> SRR2139816 1 0.000 0.990 1.00 0.00
#> SRR2139799 1 0.000 0.990 1.00 0.00
#> SRR2139777 1 0.000 0.990 1.00 0.00
#> SRR2139700 2 0.000 0.998 0.00 1.00
#> SRR2139719 2 0.000 0.998 0.00 1.00
#> SRR2139713 1 0.000 0.990 1.00 0.00
#> SRR2139837 1 0.000 0.990 1.00 0.00
#> SRR2139683 1 0.000 0.990 1.00 0.00
#> SRR2139717 2 0.000 0.998 0.00 1.00
#> SRR2139689 1 0.904 0.533 0.68 0.32
#> SRR2139833 2 0.000 0.998 0.00 1.00
#> SRR2139725 1 0.000 0.990 1.00 0.00
#> SRR2139752 1 0.000 0.990 1.00 0.00
#> SRR2139758 1 0.000 0.990 1.00 0.00
#> SRR2139820 1 0.000 0.990 1.00 0.00
#> SRR2139857 2 0.000 0.998 0.00 1.00
#> SRR2139736 1 0.000 0.990 1.00 0.00
#> SRR2139741 1 0.000 0.990 1.00 0.00
#> SRR2139774 2 0.000 0.998 0.00 1.00
#> SRR2139806 1 0.000 0.990 1.00 0.00
#> SRR2139755 1 0.000 0.990 1.00 0.00
#> SRR2139722 2 0.242 0.957 0.04 0.96
#> SRR2139728 1 0.680 0.781 0.82 0.18
#> SRR2139710 2 0.000 0.998 0.00 1.00
#> SRR2139720 1 0.000 0.990 1.00 0.00
#> SRR2139781 2 0.000 0.998 0.00 1.00
#> SRR2139744 1 0.000 0.990 1.00 0.00
#> SRR2139817 1 0.000 0.990 1.00 0.00
#> SRR2139792 1 0.000 0.990 1.00 0.00
#> SRR2139798 1 0.000 0.990 1.00 0.00
#> SRR2139701 1 0.000 0.990 1.00 0.00
#> SRR2139695 2 0.000 0.998 0.00 1.00
#> SRR2139858 2 0.000 0.998 0.00 1.00
#> SRR2139795 1 0.000 0.990 1.00 0.00
#> SRR2139676 1 0.000 0.990 1.00 0.00
#> SRR2139706 2 0.000 0.998 0.00 1.00
#> SRR2139749 1 0.000 0.990 1.00 0.00
#> SRR2139743 1 0.000 0.990 1.00 0.00
#> SRR2139786 1 0.000 0.990 1.00 0.00
#> SRR2139768 1 0.000 0.990 1.00 0.00
#> SRR2139727 2 0.000 0.998 0.00 1.00
#> SRR2139750 1 0.000 0.990 1.00 0.00
#> SRR2139848 2 0.000 0.998 0.00 1.00
#> SRR2139782 1 0.000 0.990 1.00 0.00
#> SRR2139711 1 0.000 0.990 1.00 0.00
#> SRR2139685 1 0.000 0.990 1.00 0.00
#> SRR2139788 2 0.000 0.998 0.00 1.00
#> SRR2139775 1 0.000 0.990 1.00 0.00
#> SRR2139778 1 0.000 0.990 1.00 0.00
#> SRR2139675 2 0.000 0.998 0.00 1.00
#> SRR2139796 1 0.000 0.990 1.00 0.00
#> SRR2139856 2 0.000 0.998 0.00 1.00
#> SRR2139740 1 0.000 0.990 1.00 0.00
#> SRR2139819 1 0.000 0.990 1.00 0.00
#> SRR2139785 1 0.000 0.990 1.00 0.00
#> SRR2139716 1 0.000 0.990 1.00 0.00
#> SRR2139761 1 0.000 0.990 1.00 0.00
#> SRR2139759 1 0.000 0.990 1.00 0.00
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> SRR2139787 1 0.2066 0.924 0.94 0.00 0.06
#> SRR2139769 1 0.2959 0.907 0.90 0.00 0.10
#> SRR2139680 2 0.0000 0.946 0.00 1.00 0.00
#> SRR2139714 2 0.5012 0.882 0.08 0.84 0.08
#> SRR2139763 1 0.1529 0.897 0.96 0.00 0.04
#> SRR2139808 3 0.0000 0.926 0.00 0.00 1.00
#> SRR2139707 1 0.1529 0.897 0.96 0.00 0.04
#> SRR2139699 2 0.0892 0.945 0.00 0.98 0.02
#> SRR2139677 2 0.0000 0.946 0.00 1.00 0.00
#> SRR2139794 2 0.0000 0.946 0.00 1.00 0.00
#> SRR2139742 1 0.1529 0.897 0.96 0.00 0.04
#> SRR2139748 3 0.2066 0.947 0.06 0.00 0.94
#> SRR2139732 1 0.0000 0.918 1.00 0.00 0.00
#> SRR2139745 1 0.2066 0.924 0.94 0.00 0.06
#> SRR2139738 3 0.4002 0.845 0.16 0.00 0.84
#> SRR2139816 3 0.2959 0.926 0.10 0.00 0.90
#> SRR2139799 3 0.1529 0.902 0.04 0.00 0.96
#> SRR2139777 3 0.0000 0.926 0.00 0.00 1.00
#> SRR2139700 2 0.0892 0.945 0.00 0.98 0.02
#> SRR2139719 2 0.0000 0.946 0.00 1.00 0.00
#> SRR2139713 1 0.0000 0.918 1.00 0.00 0.00
#> SRR2139837 3 0.2066 0.947 0.06 0.00 0.94
#> SRR2139683 1 0.1529 0.925 0.96 0.00 0.04
#> SRR2139717 2 0.0000 0.946 0.00 1.00 0.00
#> SRR2139689 1 0.8215 0.263 0.54 0.08 0.38
#> SRR2139833 2 0.3572 0.919 0.04 0.90 0.06
#> SRR2139725 1 0.2537 0.919 0.92 0.00 0.08
#> SRR2139752 1 0.2959 0.908 0.90 0.00 0.10
#> SRR2139758 3 0.2537 0.939 0.08 0.00 0.92
#> SRR2139820 3 0.2066 0.947 0.06 0.00 0.94
#> SRR2139857 2 0.4097 0.909 0.06 0.88 0.06
#> SRR2139736 3 0.2066 0.947 0.06 0.00 0.94
#> SRR2139741 3 0.2066 0.947 0.06 0.00 0.94
#> SRR2139774 2 0.4556 0.896 0.08 0.86 0.06
#> SRR2139806 3 0.0892 0.937 0.02 0.00 0.98
#> SRR2139755 1 0.2959 0.907 0.90 0.00 0.10
#> SRR2139722 2 0.9330 0.378 0.24 0.52 0.24
#> SRR2139728 3 0.4002 0.890 0.16 0.00 0.84
#> SRR2139710 2 0.4097 0.909 0.06 0.88 0.06
#> SRR2139720 1 0.2959 0.907 0.90 0.00 0.10
#> SRR2139781 2 0.0000 0.946 0.00 1.00 0.00
#> SRR2139744 3 0.2066 0.947 0.06 0.00 0.94
#> SRR2139817 1 0.2537 0.919 0.92 0.00 0.08
#> SRR2139792 3 0.0000 0.926 0.00 0.00 1.00
#> SRR2139798 1 0.0000 0.918 1.00 0.00 0.00
#> SRR2139701 1 0.0892 0.924 0.98 0.00 0.02
#> SRR2139695 2 0.0000 0.946 0.00 1.00 0.00
#> SRR2139858 2 0.0892 0.945 0.00 0.98 0.02
#> SRR2139795 3 0.4002 0.890 0.16 0.00 0.84
#> SRR2139676 1 0.0000 0.918 1.00 0.00 0.00
#> SRR2139706 2 0.0000 0.946 0.00 1.00 0.00
#> SRR2139749 1 0.2066 0.924 0.94 0.00 0.06
#> SRR2139743 1 0.2537 0.919 0.92 0.00 0.08
#> SRR2139786 3 0.0892 0.937 0.02 0.00 0.98
#> SRR2139768 3 0.4002 0.861 0.16 0.00 0.84
#> SRR2139727 2 0.2066 0.931 0.00 0.94 0.06
#> SRR2139750 3 0.2066 0.947 0.06 0.00 0.94
#> SRR2139848 2 0.3572 0.919 0.04 0.90 0.06
#> SRR2139782 3 0.2537 0.940 0.08 0.00 0.92
#> SRR2139711 1 0.0892 0.916 0.98 0.00 0.02
#> SRR2139685 1 0.1529 0.897 0.96 0.00 0.04
#> SRR2139788 2 0.0000 0.946 0.00 1.00 0.00
#> SRR2139775 3 0.2959 0.926 0.10 0.00 0.90
#> SRR2139778 1 0.5216 0.661 0.74 0.00 0.26
#> SRR2139675 2 0.0000 0.946 0.00 1.00 0.00
#> SRR2139796 3 0.1529 0.914 0.04 0.00 0.96
#> SRR2139856 2 0.0892 0.945 0.00 0.98 0.02
#> SRR2139740 1 0.2959 0.907 0.90 0.00 0.10
#> SRR2139819 1 0.0000 0.918 1.00 0.00 0.00
#> SRR2139785 3 0.2066 0.947 0.06 0.00 0.94
#> SRR2139716 1 0.1529 0.925 0.96 0.00 0.04
#> SRR2139761 1 0.0892 0.924 0.98 0.00 0.02
#> SRR2139759 1 0.2537 0.919 0.92 0.00 0.08
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> SRR2139787 1 0.0707 0.901 0.98 0.00 0.02 0.00
#> SRR2139769 1 0.2647 0.865 0.88 0.00 0.12 0.00
#> SRR2139680 4 0.0000 0.998 0.00 0.00 0.00 1.00
#> SRR2139714 2 0.0000 0.922 0.00 1.00 0.00 0.00
#> SRR2139763 1 0.2345 0.853 0.90 0.10 0.00 0.00
#> SRR2139808 3 0.2011 0.874 0.00 0.08 0.92 0.00
#> SRR2139707 1 0.4907 0.350 0.58 0.42 0.00 0.00
#> SRR2139699 2 0.2345 0.897 0.00 0.90 0.00 0.10
#> SRR2139677 4 0.0000 0.998 0.00 0.00 0.00 1.00
#> SRR2139794 4 0.0707 0.977 0.00 0.02 0.00 0.98
#> SRR2139742 1 0.1637 0.879 0.94 0.06 0.00 0.00
#> SRR2139748 3 0.0000 0.921 0.00 0.00 1.00 0.00
#> SRR2139732 1 0.0000 0.898 1.00 0.00 0.00 0.00
#> SRR2139745 1 0.1211 0.900 0.96 0.00 0.04 0.00
#> SRR2139738 3 0.2335 0.889 0.06 0.02 0.92 0.00
#> SRR2139816 3 0.2011 0.889 0.08 0.00 0.92 0.00
#> SRR2139799 3 0.4277 0.625 0.00 0.28 0.72 0.00
#> SRR2139777 3 0.0707 0.914 0.00 0.02 0.98 0.00
#> SRR2139700 2 0.2647 0.879 0.00 0.88 0.00 0.12
#> SRR2139719 4 0.0000 0.998 0.00 0.00 0.00 1.00
#> SRR2139713 1 0.1637 0.884 0.94 0.06 0.00 0.00
#> SRR2139837 3 0.0000 0.921 0.00 0.00 1.00 0.00
#> SRR2139683 1 0.2830 0.871 0.90 0.04 0.06 0.00
#> SRR2139717 4 0.0000 0.998 0.00 0.00 0.00 1.00
#> SRR2139689 2 0.0000 0.922 0.00 1.00 0.00 0.00
#> SRR2139833 2 0.1211 0.926 0.00 0.96 0.00 0.04
#> SRR2139725 1 0.1637 0.896 0.94 0.00 0.06 0.00
#> SRR2139752 1 0.2921 0.847 0.86 0.00 0.14 0.00
#> SRR2139758 3 0.2345 0.873 0.10 0.00 0.90 0.00
#> SRR2139820 3 0.0000 0.921 0.00 0.00 1.00 0.00
#> SRR2139857 2 0.0000 0.922 0.00 1.00 0.00 0.00
#> SRR2139736 3 0.0000 0.921 0.00 0.00 1.00 0.00
#> SRR2139741 3 0.0000 0.921 0.00 0.00 1.00 0.00
#> SRR2139774 2 0.0000 0.922 0.00 1.00 0.00 0.00
#> SRR2139806 3 0.0000 0.921 0.00 0.00 1.00 0.00
#> SRR2139755 1 0.2345 0.877 0.90 0.00 0.10 0.00
#> SRR2139722 2 0.7408 0.372 0.06 0.56 0.06 0.32
#> SRR2139728 3 0.5818 0.734 0.10 0.14 0.74 0.02
#> SRR2139710 2 0.0000 0.922 0.00 1.00 0.00 0.00
#> SRR2139720 1 0.2647 0.865 0.88 0.00 0.12 0.00
#> SRR2139781 4 0.0000 0.998 0.00 0.00 0.00 1.00
#> SRR2139744 3 0.0000 0.921 0.00 0.00 1.00 0.00
#> SRR2139817 1 0.1211 0.899 0.96 0.00 0.04 0.00
#> SRR2139792 3 0.0000 0.921 0.00 0.00 1.00 0.00
#> SRR2139798 1 0.0000 0.898 1.00 0.00 0.00 0.00
#> SRR2139701 1 0.0707 0.895 0.98 0.02 0.00 0.00
#> SRR2139695 4 0.0000 0.998 0.00 0.00 0.00 1.00
#> SRR2139858 2 0.1637 0.921 0.00 0.94 0.00 0.06
#> SRR2139795 3 0.4088 0.812 0.14 0.04 0.82 0.00
#> SRR2139676 1 0.0000 0.898 1.00 0.00 0.00 0.00
#> SRR2139706 4 0.0000 0.998 0.00 0.00 0.00 1.00
#> SRR2139749 1 0.0000 0.898 1.00 0.00 0.00 0.00
#> SRR2139743 1 0.2011 0.887 0.92 0.00 0.08 0.00
#> SRR2139786 3 0.0000 0.921 0.00 0.00 1.00 0.00
#> SRR2139768 3 0.2345 0.873 0.10 0.00 0.90 0.00
#> SRR2139727 2 0.1637 0.921 0.00 0.94 0.00 0.06
#> SRR2139750 3 0.0000 0.921 0.00 0.00 1.00 0.00
#> SRR2139848 2 0.1211 0.926 0.00 0.96 0.00 0.04
#> SRR2139782 3 0.1211 0.910 0.04 0.00 0.96 0.00
#> SRR2139711 1 0.4227 0.814 0.82 0.06 0.12 0.00
#> SRR2139685 1 0.3172 0.805 0.84 0.16 0.00 0.00
#> SRR2139788 4 0.0000 0.998 0.00 0.00 0.00 1.00
#> SRR2139775 3 0.1913 0.899 0.02 0.00 0.94 0.04
#> SRR2139778 1 0.5860 0.318 0.58 0.04 0.38 0.00
#> SRR2139675 4 0.0000 0.998 0.00 0.00 0.00 1.00
#> SRR2139796 3 0.4522 0.543 0.00 0.32 0.68 0.00
#> SRR2139856 2 0.1637 0.921 0.00 0.94 0.00 0.06
#> SRR2139740 1 0.2921 0.845 0.86 0.00 0.14 0.00
#> SRR2139819 1 0.1637 0.884 0.94 0.06 0.00 0.00
#> SRR2139785 3 0.1211 0.910 0.04 0.00 0.96 0.00
#> SRR2139716 1 0.0707 0.901 0.98 0.00 0.02 0.00
#> SRR2139761 1 0.0000 0.898 1.00 0.00 0.00 0.00
#> SRR2139759 1 0.1637 0.896 0.94 0.00 0.06 0.00
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
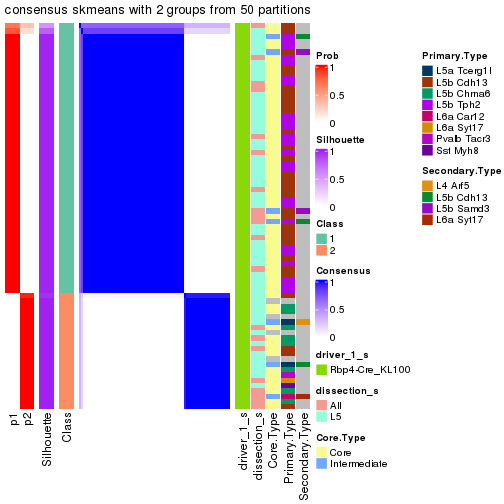
consensus_heatmap(res, k = 3)
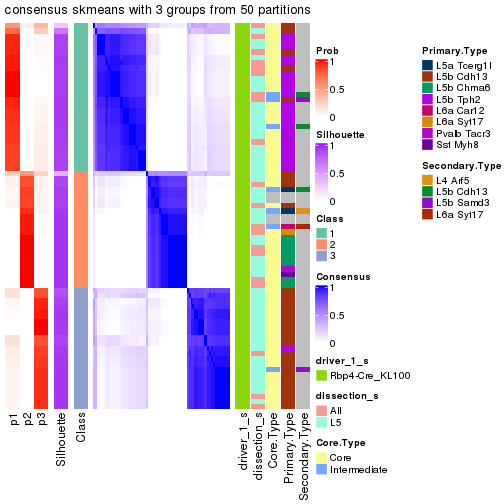
consensus_heatmap(res, k = 4)
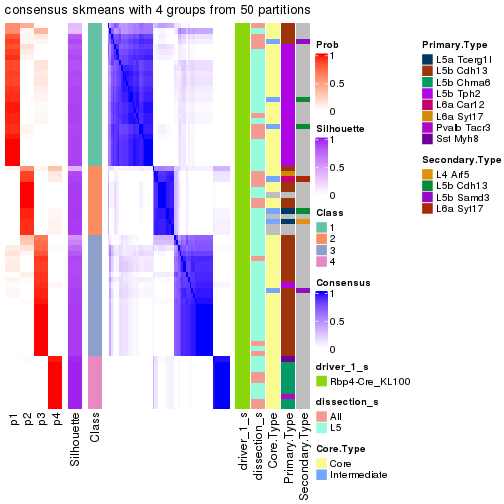
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
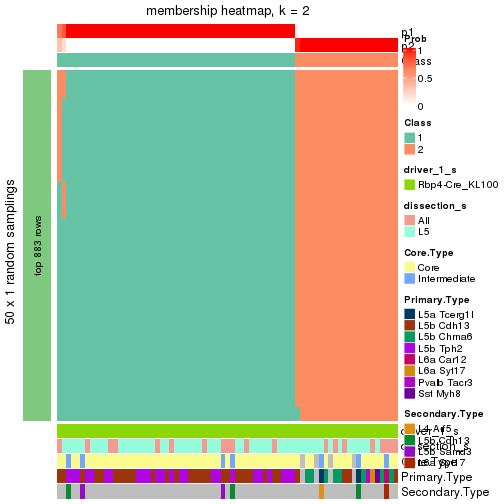
membership_heatmap(res, k = 3)
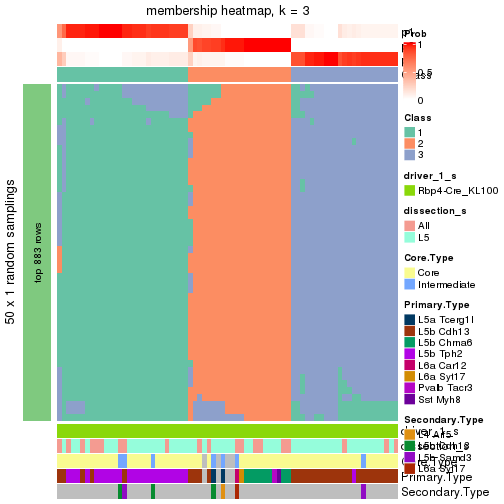
membership_heatmap(res, k = 4)
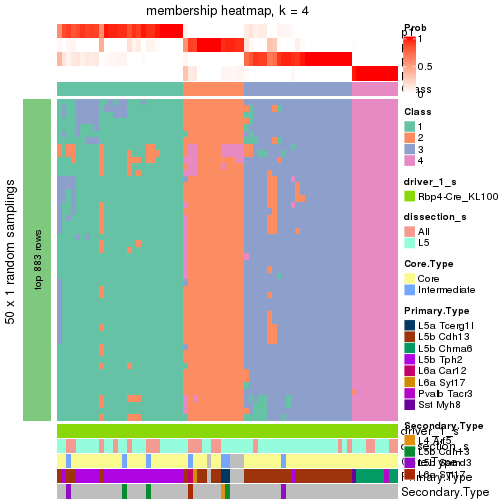
As soon as the classes for columns are determined, the signatures that are significantly different between subgroups can be looked for. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
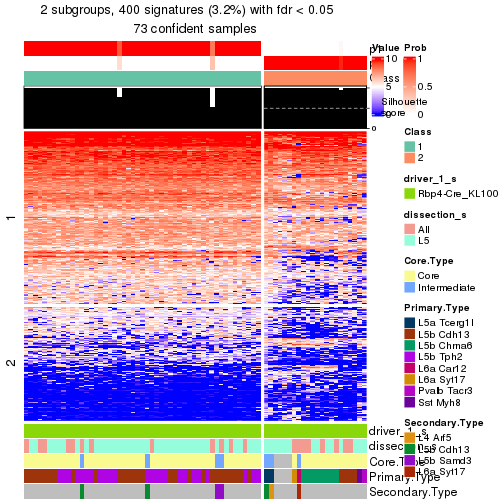
get_signatures(res, k = 3, scale_rows = FALSE)
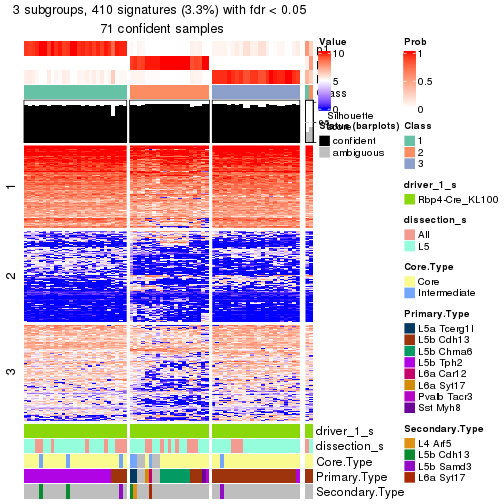
get_signatures(res, k = 4, scale_rows = FALSE)
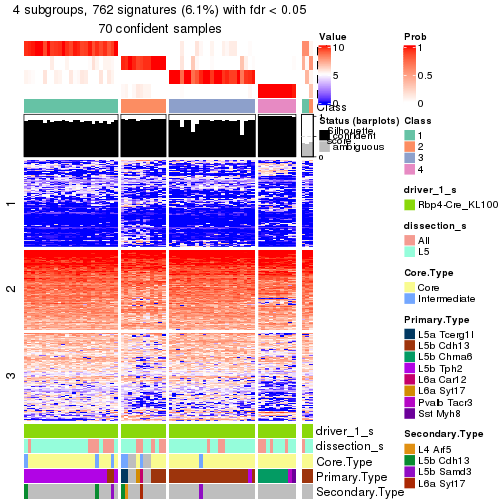
Compare the overlap of signatures from different k:
compare_signatures(res)
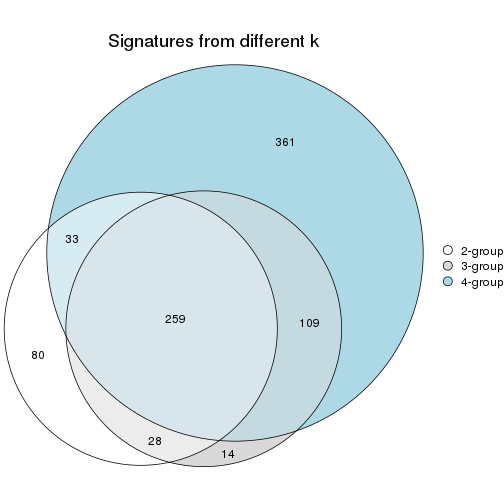
get_signature() returns a data frame invisibly. To get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows (which is done by automatically selecting number of clusters).If there are too many signatures, top_signatures = ... can be set to only show the
signatures with the highest FDRs:
# code only for demonstration
# e.g. to show the top 500 most significant rows
tb = get_signature(res, k = ..., top_signatures = 500)
If the signatures are defined as these which are uniquely high in current group, diff_method argument
can be set to "uniquely_high_in_one_group":
# code only for demonstration
tb = get_signature(res, k = ..., diff_method = "uniquely_high_in_one_group")
UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
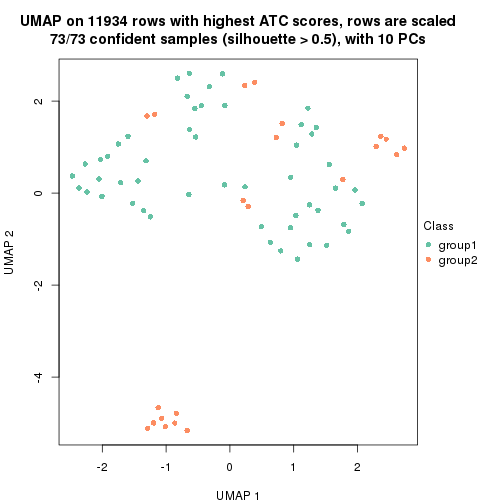
dimension_reduction(res, k = 3, method = "UMAP")
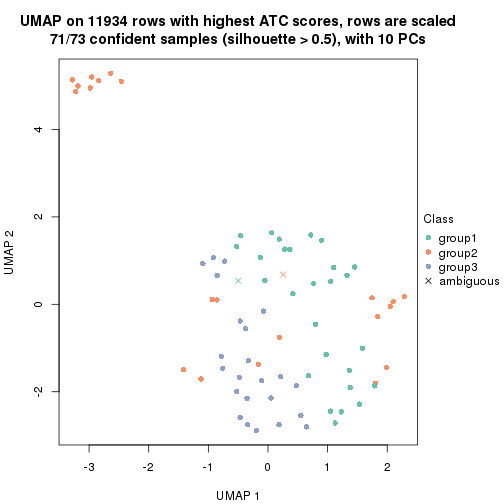
dimension_reduction(res, k = 4, method = "UMAP")
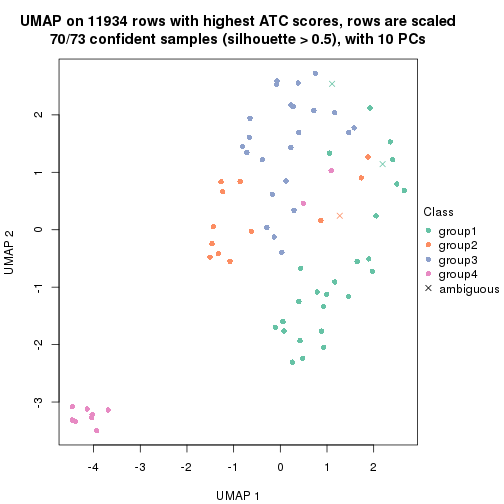
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
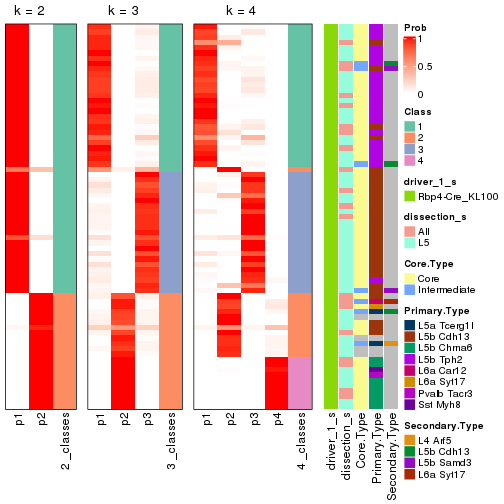
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n_sample driver_1_s(p-value) dissection_s(p-value) Core.Type(p-value)
#> ATC:skmeans 73 NA 0.400 0.5406
#> ATC:skmeans 71 NA 0.157 0.3928
#> ATC:skmeans 70 NA 0.218 0.0404
#> Primary.Type(p-value) Secondary.Type(p-value) k
#> ATC:skmeans 9.48e-09 0.1605 2
#> ATC:skmeans 6.06e-14 0.3957 3
#> ATC:skmeans 1.01e-20 0.0792 4
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
sessionInfo()
#> R version 4.1.0 (2021-05-18)
#> Platform: x86_64-pc-linux-gnu (64-bit)
#> Running under: CentOS Linux 7 (Core)
#>
#> Matrix products: default
#> BLAS/LAPACK: /usr/lib64/libopenblas-r0.3.3.so
#>
#> locale:
#> [1] LC_CTYPE=en_US.UTF-8 LC_NUMERIC=C LC_TIME=en_US.UTF-8
#> [4] LC_COLLATE=en_US.UTF-8 LC_MONETARY=en_US.UTF-8 LC_MESSAGES=en_US.UTF-8
#> [7] LC_PAPER=en_US.UTF-8 LC_NAME=C LC_ADDRESS=C
#> [10] LC_TELEPHONE=C LC_MEASUREMENT=en_US.UTF-8 LC_IDENTIFICATION=C
#>
#> attached base packages:
#> [1] grid parallel stats4 stats graphics grDevices utils datasets methods
#> [10] base
#>
#> other attached packages:
#> [1] genefilter_1.74.0 ComplexHeatmap_2.8.0 markdown_1.1
#> [4] knitr_1.33 scRNAseq_2.6.1 SingleCellExperiment_1.14.1
#> [7] SummarizedExperiment_1.22.0 Biobase_2.52.0 GenomicRanges_1.44.0
#> [10] GenomeInfoDb_1.28.1 IRanges_2.26.0 S4Vectors_0.30.0
#> [13] BiocGenerics_0.38.0 MatrixGenerics_1.4.0 matrixStats_0.59.0
#> [16] cola_1.9.4
#>
#> loaded via a namespace (and not attached):
#> [1] circlize_0.4.13 AnnotationHub_3.0.1 BiocFileCache_2.0.0
#> [4] lazyeval_0.2.2 polylabelr_0.2.0 splines_4.1.0
#> [7] Polychrome_1.3.1 BiocParallel_1.26.1 ggplot2_3.3.5
#> [10] digest_0.6.27 foreach_1.5.1 ensembldb_2.16.3
#> [13] htmltools_0.5.1.1 viridis_0.6.1 fansi_0.5.0
#> [16] magrittr_2.0.1 memoise_2.0.0 cluster_2.1.2
#> [19] doParallel_1.0.16 Biostrings_2.60.1 annotate_1.70.0
#> [22] askpass_1.1 prettyunits_1.1.1 colorspace_2.0-2
#> [25] blob_1.2.1 rappdirs_0.3.3 xfun_0.24
#> [28] dplyr_1.0.7 crayon_1.4.1 RCurl_1.98-1.3
#> [31] microbenchmark_1.4-7 jsonlite_1.7.2 impute_1.66.0
#> [34] brew_1.0-6 survival_3.2-11 iterators_1.0.13
#> [37] glue_1.4.2 polyclip_1.10-0 gtable_0.3.0
#> [40] zlibbioc_1.38.0 XVector_0.32.0 GetoptLong_1.0.5
#> [43] DelayedArray_0.18.0 shape_1.4.6 scales_1.1.1
#> [46] data.tree_1.0.0 DBI_1.1.1 Rcpp_1.0.7
#> [49] viridisLite_0.4.0 xtable_1.8-4 progress_1.2.2
#> [52] clue_0.3-59 reticulate_1.20 bit_4.0.4
#> [55] mclust_5.4.7 umap_0.2.7.0 httr_1.4.2
#> [58] RColorBrewer_1.1-2 ellipsis_0.3.2 pkgconfig_2.0.3
#> [61] XML_3.99-0.6 dbplyr_2.1.1 utf8_1.2.1
#> [64] tidyselect_1.1.1 rlang_0.4.11 later_1.2.0
#> [67] AnnotationDbi_1.54.1 munsell_0.5.0 BiocVersion_3.13.1
#> [70] tools_4.1.0 cachem_1.0.5 generics_0.1.0
#> [73] RSQLite_2.2.7 ExperimentHub_2.0.0 evaluate_0.14
#> [76] stringr_1.4.0 fastmap_1.1.0 yaml_2.2.1
#> [79] bit64_4.0.5 purrr_0.3.4 dendextend_1.15.1
#> [82] KEGGREST_1.32.0 AnnotationFilter_1.16.0 mime_0.11
#> [85] slam_0.1-48 xml2_1.3.2 biomaRt_2.48.2
#> [88] compiler_4.1.0 rstudioapi_0.13 filelock_1.0.2
#> [91] curl_4.3.2 png_0.1-7 interactiveDisplayBase_1.30.0
#> [94] tibble_3.1.2 stringi_1.7.3 highr_0.9
#> [97] GenomicFeatures_1.44.0 RSpectra_0.16-0 lattice_0.20-44
#> [100] ProtGenerics_1.24.0 Matrix_1.3-4 vctrs_0.3.8
#> [103] pillar_1.6.1 lifecycle_1.0.0 BiocManager_1.30.16
#> [106] eulerr_6.1.0 GlobalOptions_0.1.2 bitops_1.0-7
#> [109] irlba_2.3.3 httpuv_1.6.1 rtracklayer_1.52.0
#> [112] R6_2.5.0 BiocIO_1.2.0 promises_1.2.0.1
#> [115] gridExtra_2.3 codetools_0.2-18 assertthat_0.2.1
#> [118] openssl_1.4.4 rjson_0.2.20 GenomicAlignments_1.28.0
#> [121] Rsamtools_2.8.0 GenomeInfoDbData_1.2.6 hms_1.1.0
#> [124] skmeans_0.2-13 Cairo_1.5-12.2 scatterplot3d_0.3-41
#> [127] shiny_1.6.0 restfulr_0.0.13