
Date: 2021-07-26 10:50:21 CEST, cola version: 1.9.4
Document is loading... 
First the variable is renamed to res_rh.
res_rh = rh
The partition hierarchy and all available functions which can be applied to res_rh object.
res_rh
#> A 'HierarchicalPartition' object with 'ATC:skmeans' method.
#> On a matrix with 14607 rows and 638 columns.
#> Performed in total 5400 partitions.
#> There are 22 groups under the following parameters:
#> - min_samples: 6
#> - mean_silhouette_cutoff: 0.9
#> - min_n_signatures: 143 (signatures are selected based on:)
#> - fdr_cutoff: 0.05
#> - group_diff (scaled values): 0.5
#>
#> Hierarchy of the partition:
#> 0, 638 cols
#> |-- 01, 377 cols, 1587 signatures
#> | |-- 011, 207 cols, 2764 signatures
#> | | |-- 0111, 73 cols, 256 signatures
#> | | | |-- 01111, 38 cols, 3 signatures (c)
#> | | | `-- 01112, 35 cols (a)
#> | | |-- 0112, 71 cols, 388 signatures
#> | | | |-- 01121, 32 cols, 37 signatures (c)
#> | | | `-- 01122, 39 cols, 1 signatures (c)
#> | | `-- 0113, 63 cols, 249 signatures
#> | | |-- 01131, 39 cols (a)
#> | | `-- 01132, 24 cols, 181 signatures
#> | | |-- 011321, 16 cols, 0 signatures (c)
#> | | `-- 011322, 8 cols (b)
#> | `-- 012, 170 cols, 4252 signatures
#> | |-- 0121, 59 cols, 79 signatures (c)
#> | |-- 0122, 40 cols, 545 signatures
#> | | |-- 01221, 15 cols, 16 signatures (c)
#> | | |-- 01222, 15 cols, 71 signatures (c)
#> | | `-- 01223, 10 cols (b)
#> | |-- 0123, 36 cols, 373 signatures
#> | | |-- 01231, 18 cols, 0 signatures (c)
#> | | `-- 01232, 18 cols, 0 signatures (c)
#> | `-- 0124, 35 cols, 13 signatures (c)
#> `-- 02, 261 cols, 5379 signatures
#> |-- 021, 90 cols, 1013 signatures
#> | |-- 0211, 48 cols, 2 signatures (c)
#> | `-- 0212, 42 cols, 13 signatures (c)
#> |-- 022, 76 cols, 903 signatures
#> | |-- 0221, 34 cols, 80 signatures (c)
#> | `-- 0222, 42 cols, 56 signatures (c)
#> |-- 023, 43 cols, 507 signatures
#> | |-- 0231, 17 cols, 1 signatures (c)
#> | |-- 0232, 12 cols, 46 signatures (c)
#> | `-- 0233, 14 cols, 0 signatures (c)
#> `-- 024, 52 cols, 36 signatures (c)
#> Stop reason:
#> a) Mean silhouette score was too small
#> b) Subgroup had too few columns.
#> c) There were too few signatures.
#>
#> Following methods can be applied to this 'HierarchicalPartition' object:
#> [1] "all_leaves" "all_nodes" "cola_report" "collect_classes"
#> [5] "colnames" "compare_signatures" "dimension_reduction" "functional_enrichment"
#> [9] "get_anno_col" "get_anno" "get_children_nodes" "get_classes"
#> [13] "get_matrix" "get_signatures" "is_leaf_node" "max_depth"
#> [17] "merge_node" "ncol" "node_info" "node_level"
#> [21] "nrow" "rownames" "show" "split_node"
#> [25] "suggest_best_k" "test_to_known_factors" "top_rows_heatmap" "top_rows_overlap"
#>
#> You can get result for a single node by e.g. object["01"]
The call of hierarchical_partition() was:
#> hierarchical_partition(data = lt$mat, anno = lt$anno, subset = 500, cores = 4)
Dimension of the input matrix:
mat = get_matrix(res_rh)
dim(mat)
#> [1] 14607 638
All the methods that were tried:
res_rh@param$combination_method
#> [[1]]
#> [1] "ATC" "skmeans"
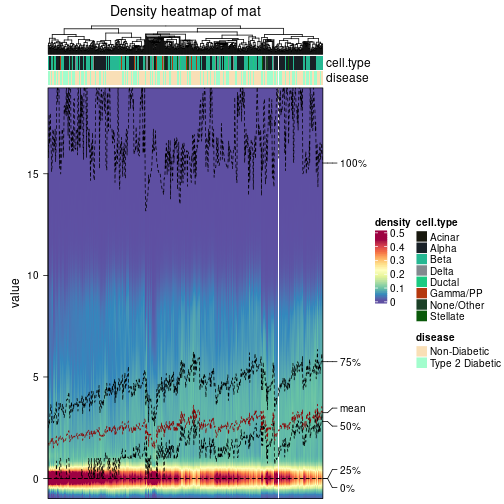
The density distribution for each sample is visualized as one column in the following heatmap. The clustering is based on the distance which is the Kolmogorov-Smirnov statistic between two distributions.
library(ComplexHeatmap)
densityHeatmap(mat, top_annotation = HeatmapAnnotation(df = get_anno(res_rh),
col = get_anno_col(res_rh)), ylab = "value", cluster_columns = TRUE, show_column_names = FALSE,
mc.cores = 1)
Some values about the hierarchy:
all_nodes(res_rh)
#> [1] "0" "01" "011" "0111" "01111" "01112" "0112" "01121" "01122" "0113"
#> [11] "01131" "01132" "011321" "011322" "012" "0121" "0122" "01221" "01222" "01223"
#> [21] "0123" "01231" "01232" "0124" "02" "021" "0211" "0212" "022" "0221"
#> [31] "0222" "023" "0231" "0232" "0233" "024"
all_leaves(res_rh)
#> [1] "01111" "01112" "01121" "01122" "01131" "011321" "011322" "0121" "01221" "01222"
#> [11] "01223" "01231" "01232" "0124" "0211" "0212" "0221" "0222" "0231" "0232"
#> [21] "0233" "024"
node_info(res_rh)
#> id best_method depth best_k n_columns n_signatures p_signatures is_leaf
#> 1 0 ATC:skmeans 1 2 638 2868 1.96e-01 FALSE
#> 2 01 ATC:skmeans 2 2 377 1587 1.09e-01 FALSE
#> 3 011 ATC:skmeans 3 3 207 2764 1.89e-01 FALSE
#> 4 0111 ATC:skmeans 4 2 73 256 1.75e-02 FALSE
#> 5 01111 ATC:skmeans 5 2 38 3 2.05e-04 TRUE
#> 6 01112 ATC:skmeans 5 2 35 NA NA TRUE
#> 7 0112 ATC:skmeans 4 2 71 388 2.66e-02 FALSE
#> 8 01121 ATC:skmeans 5 2 32 37 2.53e-03 TRUE
#> 9 01122 ATC:skmeans 5 2 39 1 6.85e-05 TRUE
#> 10 0113 ATC:skmeans 4 2 63 249 1.70e-02 FALSE
#> 11 01131 ATC:skmeans 5 2 39 NA NA TRUE
#> 12 01132 ATC:skmeans 5 2 24 181 1.24e-02 FALSE
#> 13 011321 ATC:skmeans 6 2 16 0 0.00e+00 TRUE
#> 14 011322 not applied 6 NA 8 NA NA TRUE
#> 15 012 ATC:skmeans 3 4 170 4252 2.91e-01 FALSE
#> 16 0121 ATC:skmeans 4 2 59 79 5.41e-03 TRUE
#> 17 0122 ATC:skmeans 4 3 40 545 3.73e-02 FALSE
#> 18 01221 ATC:skmeans 5 2 15 16 1.10e-03 TRUE
#> 19 01222 ATC:skmeans 5 2 15 71 4.86e-03 TRUE
#> 20 01223 not applied 5 NA 10 NA NA TRUE
#> 21 0123 ATC:skmeans 4 2 36 373 2.55e-02 FALSE
#> 22 01231 ATC:skmeans 5 2 18 0 0.00e+00 TRUE
#> 23 01232 ATC:skmeans 5 2 18 0 0.00e+00 TRUE
#> 24 0124 ATC:skmeans 4 2 35 13 8.90e-04 TRUE
#> 25 02 ATC:skmeans 2 4 261 5379 3.68e-01 FALSE
#> 26 021 ATC:skmeans 3 2 90 1013 6.94e-02 FALSE
#> 27 0211 ATC:skmeans 4 2 48 2 1.37e-04 TRUE
#> 28 0212 ATC:skmeans 4 2 42 13 8.90e-04 TRUE
#> 29 022 ATC:skmeans 3 2 76 903 6.18e-02 FALSE
#> 30 0221 ATC:skmeans 4 3 34 80 5.48e-03 TRUE
#> 31 0222 ATC:skmeans 4 2 42 56 3.83e-03 TRUE
#> 32 023 ATC:skmeans 3 3 43 507 3.47e-02 FALSE
#> 33 0231 ATC:skmeans 4 2 17 1 6.85e-05 TRUE
#> 34 0232 ATC:skmeans 4 3 12 46 3.15e-03 TRUE
#> 35 0233 ATC:skmeans 4 2 14 0 0.00e+00 TRUE
#> 36 024 ATC:skmeans 3 2 52 36 2.46e-03 TRUE
In the output from node_info(), there are the following columns:
id: The node id.best_method: The best method selected.depth: Depth of the node in the hierarchy.best_k: Best number of groups of the partition on that node.n_columns: Number of columns in the submatrix.n_signatures: Number of signatures with the best_k.p_signatures: Proportion of hte signatures in total number of rows in the matrix.is_leaf: Whether the node is a leaf.Labels of nodes are encoded in a special way. The number of digits correspond to the depth of the node in the hierarchy and the value of the digits correspond to the index of the subgroup in the current node, E.g. a label of “012” means the node is the second subgroup of the partition which is the first subgroup of the root node.
Following table shows the best k (number of partitions) for each node in the
partition hierarchy. Clicking on the node name in the table goes to the
corresponding section for the partitioning on that node.
The cola vignette explains the definition of the metrics used for determining the best number of partitions.
suggest_best_k(res_rh)
| Node | Best method | Is leaf | Best k | 1-PAC | Mean silhouette | Concordance | #samples | |
|---|---|---|---|---|---|---|---|---|
| Node0 | ATC:skmeans | 4 | 0.94 | 0.90 | 0.96 | 638 | * | |
| Node01 | ATC:skmeans | 4 | 0.98 | 0.94 | 0.97 | 377 | ** | |
| Node011 | ATC:skmeans | 4 | 0.92 | 0.90 | 0.95 | 207 | * | |
| Node0111 | ATC:skmeans | 2 | 1.00 | 0.96 | 0.98 | 73 | ** | |
| Node01111-leaf | ATC:skmeans | ✓ (c) | 2 | 0.86 | 0.93 | 0.96 | 38 | |
| Node01112-leaf | ATC:skmeans | ✓ (a) | 2 | 0.67 | 0.83 | 0.93 | 35 | |
| Node0112 | ATC:skmeans | 2 | 1.00 | 0.97 | 0.99 | 71 | ** | |
| Node01121-leaf | ATC:skmeans | ✓ (c) | 2 | 1.00 | 1.00 | 1.00 | 32 | ** |
| Node01122-leaf | ATC:skmeans | ✓ (c) | 2 | 0.84 | 0.92 | 0.97 | 39 | |
| Node0113 | ATC:skmeans | 2 | 1.00 | 0.99 | 0.99 | 63 | ** | |
| Node01131-leaf | ATC:skmeans | ✓ (a) | 2 | 0.38 | 0.80 | 0.90 | 39 | |
| Node01132 | ATC:skmeans | 2 | 1.00 | 0.99 | 1.00 | 24 | ** | |
| Node011321-leaf | ATC:skmeans | ✓ (c) | 2 | 0.88 | 0.95 | 0.98 | 16 | |
| Node011322-leaf | not applied | ✓ (b) | 8 | |||||
| Node012 | ATC:skmeans | 4 | 1.00 | 0.98 | 0.99 | 170 | ** | |
| Node0121-leaf | ATC:skmeans | ✓ (c) | 2 | 0.96 | 0.95 | 0.98 | 59 | ** |
| Node0122 | ATC:skmeans | 3 | 1.00 | 0.97 | 0.99 | 40 | ** | |
| Node01221-leaf | ATC:skmeans | ✓ (c) | 2 | 0.87 | 0.97 | 0.99 | 15 | |
| Node01222-leaf | ATC:skmeans | ✓ (c) | 3 | 1.00 | 0.99 | 0.99 | 15 | ** |
| Node01223-leaf | not applied | ✓ (b) | 10 | |||||
| Node0123 | ATC:skmeans | 4 | 0.97 | 0.95 | 0.97 | 36 | ** | |
| Node01231-leaf | ATC:skmeans | ✓ (c) | 2 | 1.00 | 1.00 | 1.00 | 18 | ** |
| Node01232-leaf | ATC:skmeans | ✓ (c) | 2 | 1.00 | 1.00 | 1.00 | 18 | ** |
| Node0124-leaf | ATC:skmeans | ✓ (c) | 2 | 1.00 | 0.98 | 0.99 | 35 | ** |
| Node02 | ATC:skmeans | 4 | 1.00 | 0.98 | 0.99 | 261 | ** | |
| Node021 | ATC:skmeans | 2 | 1.00 | 0.97 | 0.99 | 90 | ** | |
| Node0211-leaf | ATC:skmeans | ✓ (c) | 2 | 0.96 | 0.96 | 0.98 | 48 | ** |
| Node0212-leaf | ATC:skmeans | ✓ (c) | 2 | 0.95 | 0.90 | 0.96 | 42 | * |
| Node022 | ATC:skmeans | 2 | 1.00 | 1.00 | 1.00 | 76 | ** | |
| Node0221-leaf | ATC:skmeans | ✓ (c) | 3 | 1.00 | 0.98 | 0.99 | 34 | ** |
| Node0222-leaf | ATC:skmeans | ✓ (c) | 3 | 0.96 | 0.93 | 0.97 | 42 | ** |
| Node023 | ATC:skmeans | 3 | 0.94 | 0.96 | 0.98 | 43 | * | |
| Node0231-leaf | ATC:skmeans | ✓ (c) | 2 | 1.00 | 0.99 | 0.99 | 17 | ** |
| Node0232-leaf | ATC:skmeans | ✓ (c) | 3 | 0.83 | 0.94 | 0.97 | 12 | |
| Node0233-leaf | ATC:skmeans | ✓ (c) | 3 | 1.00 | 0.95 | 0.96 | 14 | ** |
| Node024-leaf | ATC:skmeans | ✓ (c) | 2 | 0.92 | 0.95 | 0.98 | 52 | * |
Stop reason: a) Mean silhouette score was too small b) Subgroup had too few columns. c) There were too few signatures.
**: 1-PAC > 0.95, *: 1-PAC > 0.9
The nodes of the hierarchy can be merged by setting the merge_node parameters. Here we
control the hierarchy with the min_n_signatures parameter. The value of min_n_signatures is
from node_info().
collect_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 181))
#> Error in dimnames(x) <- dn: length of 'dimnames' [2] not equal to array extent
collect_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 249))
#> Error in dimnames(x) <- dn: length of 'dimnames' [2] not equal to array extent
collect_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 256))
#> Error in dimnames(x) <- dn: length of 'dimnames' [2] not equal to array extent
collect_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 373))
#> Error in dimnames(x) <- dn: length of 'dimnames' [2] not equal to array extent
collect_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 388))
#> Error in dimnames(x) <- dn: length of 'dimnames' [2] not equal to array extent
collect_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 507))
#> Error in dimnames(x) <- dn: length of 'dimnames' [2] not equal to array extent
collect_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 545))
#> Error in dimnames(x) <- dn: length of 'dimnames' [2] not equal to array extent
collect_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 903))
#> Error in dimnames(x) <- dn: length of 'dimnames' [2] not equal to array extent
collect_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 1013))
#> Error in dimnames(x) <- dn: length of 'dimnames' [2] not equal to array extent
collect_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 1587))
#> Error in dimnames(x) <- dn: length of 'dimnames' [2] not equal to array extent
collect_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 2764))
#> Error in dimnames(x) <- dn: length of 'dimnames' [2] not equal to array extent
collect_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 2868))
#> Error in dimnames(x) <- dn: length of 'dimnames' [2] not equal to array extent
collect_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 4252))
#> Error in dimnames(x) <- dn: length of 'dimnames' [2] not equal to array extent
collect_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 5379))
#> Error in dimnames(x) <- dn: length of 'dimnames' [2] not equal to array extent
Following shows the table of the partitions (You need to click the show/hide code output link to see it).
get_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 181))
#> 10th_C10_S104 10th_C11_S96 10th_C13_S61 10th_C14_S53 10th_C16_S105 10th_C17_S97 10th_C19_S62
#> "01231" "0211" "01112" "0124" "01231" "0211" "011322"
#> 10th_C1_S59 10th_C20_S54 10th_C23_S98 10th_C24_S90 10th_C28_S91 10th_C30_S107 10th_C31_S48
#> "0124" "0124" "01232" "01231" "0222" "0121" "0121"
#> 10th_C32_S56 10th_C33_S64 10th_C34_S92 10th_C37_S49 10th_C41_S101 10th_C42_S109 10th_C43_S50
#> "0211" "0211" "024" "0211" "01232" "0231" "0221"
#> 10th_C45_S66 10th_C46_S94 10th_C4_S103 10th_C50_S73 10th_C51_S80 10th_C52_S110 10th_C53_S118
#> "0121" "01222" "01221" "024" "0221" "024" "0221"
#> 10th_C54_S124 10th_C56_S74 10th_C57_S81 10th_C58_S111 10th_C5_S95 10th_C61_S68 10th_C63_S82
#> "01231" "01222" "0222" "0222" "0221" "0211" "0231"
#> 10th_C64_S112 10th_C66_S126 10th_C68_S75 10th_C6_S88 10th_C73_S84 10th_C74_S76 10th_C76_S128
#> "0211" "0211" "01231" "0222" "01221" "0121" "0124"
#> 10th_C77_S120 10th_C78_S114 10th_C7_S60 10th_C80_S77 10th_C81_S70 10th_C84_S115 10th_C85_S86
#> "0232" "0222" "01221" "0233" "01131" "01131" "0124"
#> 10th_C86_S78 10th_C87_S71 10th_C88_S130 10th_C8_S52 10th_C90_S116 10th_C95_S123 10th_C96_S117
#> "0231" "0231" "01221" "01232" "0121" "024" "0121"
#> 11th-C10_S63 11th-C12_S47 11th-C16_S64 11th-C21_S4 11th-C22_S65 11th-C24_S49 11th-C26_S12
#> "0222" "024" "01231" "0212" "0211" "01221" "0233"
#> 11th-C27_S19 11th-C2_S8 11th-C30_S66 11th-C33_S20 11th-C36_S67 11th-C37_S6 11th-C39_S21
#> "0212" "0232" "0222" "01231" "01232" "0221" "01232"
#> 11th-C40_S52 11th-C41_S60 11th-C43_S7 11th-C44_S15 11th-C49_S23 11th-C4_S62 11th-C51_S39
#> "01222" "011321" "0233" "01131" "01131" "0233" "01131"
#> 11th-C53_S78 11th-C54_S86 11th-C55_S24 11th-C56_S32 11th-C57_S40 11th-C58_S71 11th-C5_S54
#> "01131" "0212" "0233" "0232" "024" "01221" "0121"
#> 11th-C61_S25 11th-C62_S33 11th-C64_S72 11th-C66_S88 11th-C67_S26 11th-C68_S34 11th-C77_S82
#> "01232" "0222" "0231" "01112" "0221" "01221" "0232"
#> 11th-C7_S16 11th-C93_S30 12th-C10_S155 12th-C11_S147 12th-C12_S139 12th-C14_S190 12th-C15_S183
#> "011322" "0222" "0211" "0121" "0124" "01131" "0211"
#> 12th-C1_S195 12th-C20_S191 12th-C21_S184 12th-C23_S149 12th-C24_S141 12th-C25_S185 12th-C26_S192
#> "0221" "01232" "0211" "0221" "01131" "0124" "0124"
#> 12th-C28_S142 12th-C29_S150 12th-C30_S157 12th-C33_S200 12th-C35_S151 12th-C36_S158 12th-C37_S187
#> "0121" "01122" "0124" "0124" "0211" "0232" "0222"
#> 12th-C38_S194 12th-C39_S201 12th-C3_S181 12th-C40_S144 12th-C42_S159 12th-C46_S145 12th-C47_S153
#> "0211" "0221" "0211" "0221" "01131" "01222" "0211"
#> 12th-C48_S160 12th-C4_S154 12th-C50_S210 12th-C51_S217 12th-C53_S168 12th-C55_S203 12th-C56_S211
#> "0124" "0221" "024" "0124" "0231" "011321" "0233"
#> 12th-C57_S218 12th-C58_S162 12th-C59_S169 12th-C60_S176 12th-C63_S219 12th-C64_S163 12th-C65_S170
#> "024" "01121" "01112" "01112" "0121" "01112" "01131"
#> 12th-C67_S205 12th-C69_S135 12th-C71_S171 12th-C74_S214 12th-C75_S206 12th-C76_S177 12th-C7_S196
#> "0212" "01222" "0221" "01112" "0221" "01112" "01131"
#> 12th-C80_S215 12th-C81_S207 12th-C84_S165 12th-C85_S137 12th-C8_S189 12th-C90_S166 12th-C93_S209
#> "0121" "0121" "01112" "01232" "0221" "01131" "0212"
#> 12th-C94_S180 12th-C95_S174 12th-C96_S167 13th_C12_S178 13th_C13_S149 13th_C15_S134 13th_C16_S193
#> "01222" "01121" "01112" "0124" "0121" "0212" "0124"
#> 13th_C17_S186 13th_C18_S179 13th_C1_S147 13th_C20_S142 13th_C21_S135 13th_C23_S187 13th_C27_S151
#> "0222" "0222" "0221" "0221" "0222" "01222" "0231"
#> 13th_C29_S188 13th_C31_S137 13th_C34_S181 13th_C36_S196 13th_C38_S145 13th_C39_S153 13th_C3_S132
#> "0221" "0222" "01131" "0232" "0221" "0124" "0221"
#> 13th_C46_S183 13th_C49_S155 13th_C4_S191 13th_C51_S170 13th_C52_S198 13th_C53_S205 13th_C54_S212
#> "0221" "0233" "0221" "0222" "0222" "0221" "0221"
#> 13th_C55_S156 13th_C57_S171 13th_C5_S184 13th_C60_S213 13th_C63_S172 13th_C66_S214 13th_C68_S165
#> "0222" "0211" "0222" "0121" "0222" "01122" "0222"
#> 13th_C69_S173 13th_C6_S177 13th_C70_S201 13th_C71_S208 13th_C72_S215 13th_C75_S159 13th_C76_S216
#> "0222" "0221" "0222" "0222" "0232" "0211" "01122"
#> 13th_C77_S209 13th_C79_S174 13th_C80_S167 13th_C81_S160 13th_C86_S168 13th_C88_S218 13th_C89_S211
#> "0221" "0222" "0212" "0212" "0221" "0222" "0222"
#> 13th_C8_S140 13th_C92_S169 13th_C93_S162 13th_C94_S219 13th_C96_S204 1st-61_S27 1st-C11_S58
#> "0233" "0221" "0221" "0124" "0124" "01111" "01112"
#> 1st-C13_S19 1st-C15_S3 1st-C18_S51 1st-C19_S20 1st-C20_S12 1st-C21_S4 1st-C32_S14
#> "0212" "0222" "024" "01122" "024" "0121" "011321"
#> 1st-C34_S54 1st-C39_S23 1st-C42_S71 1st-C50_S33 1st-C51_S41 1st-C53_S74 1st-C56_S34
#> "01222" "0212" "011322" "01122" "024" "024" "01121"
#> 1st-C57_S42 1st-C58_S76 1st-C59_S77 1st-C62_S35 1st-C64_S79 1st-C68_S36 1st-C69_S44
#> "01122" "01111" "024" "024" "01112" "01121" "0124"
#> 1st-C71_S83 1st-C73_S45 1st-C74_S37 1st-C75_S29 1st-C77_S86 1st-C78_S85 1st-C79_S46
#> "0121" "01122" "024" "01122" "011321" "01122" "0212"
#> 1st-C80_S38 1st-C8_S10 1st-C90_S91 1st-C96_S94 2nd-C11_S20 2nd-C15_S25 2nd-C16_S33
#> "01121" "024" "01112" "0211" "01121" "01112" "01121"
#> 2nd-C17_S32 2nd-C19_S39 2nd-C1_S3 2nd-C21_S37 2nd-C25_S49 2nd-C26_S50 2nd-C27_S51
#> "01112" "0212" "0222" "011322" "01232" "01121" "0212"
#> 2nd-C28_S55 2nd-C29_S56 2nd-C2_S2 2nd-C31_S61 2nd-C32_S62 2nd-C36_S69 2nd-C37_S73
#> "024" "0121" "0232" "0121" "01112" "024" "0211"
#> 2nd-C38_S74 2nd-C39_S75 2nd-C3_S1 2nd-C47_S92 2nd-C49_S4 2nd-C4_S9 2nd-C51_S6
#> "01112" "01121" "024" "0121" "0211" "024" "0212"
#> 2nd-C52_S10 2nd-C54_S12 2nd-C57_S18 2nd-C58_S22 2nd-C5_S8 2nd-C62_S29 2nd-C67_S40
#> "0212" "01222" "0121" "024" "0212" "01111" "01122"
#> 2nd-C69_S42 2nd-C6_S7 2nd-C72_S48 2nd-C74_S53 2nd-C75_S52 2nd-C76_S60 2nd-C77_S59
#> "0222" "0121" "01112" "0121" "01121" "01232" "01122"
#> 2nd-C7_S15 2nd-C80_S65 2nd-C81_S64 2nd-C83_S71 2nd-C86_S77 2nd-C87_S76 2nd-C88_S84
#> "0212" "01121" "0124" "0121" "011321" "0211" "01112"
#> 2nd-C8_S14 2nd-C93_S88 2nd-C94_S96 2nd-C95_S95 3rd-C11_S58 3rd-C12_S68 3rd-C18_S80
#> "01122" "01112" "0222" "011321" "01111" "01122" "0121"
#> 3rd-C1_S39 3rd-C20_S22 3rd-C21_S11 3rd-C23_S94 3rd-C25_S15 3rd-C26_S28 3rd-C27_S49
#> "01232" "01231" "0121" "024" "0212" "0121" "01122"
#> 3rd-C32_S31 3rd-C33_S50 3rd-C35_S23 3rd-C36_S2 3rd-C3_S2 3rd-C40_S57 3rd-C42_S74
#> "024" "01111" "011322" "01111" "024" "0124" "01222"
#> 3rd-C44_S32 3rd-C46_S93 3rd-C47_S35 3rd-C49_S60 3rd-C4_S25 3rd-C51_S87 3rd-C52_S86
#> "024" "01232" "01122" "01122" "01111" "0232" "024"
#> 3rd-C53_S67 3rd-C56_S90 3rd-C57_S5 3rd-C58_S3 3rd-C59_S91 3rd-C60_S10 3rd-C61_S64
#> "01112" "0212" "01121" "01111" "01111" "0211" "024"
#> 3rd-C63_S54 3rd-C65_S20 3rd-C67_S69 3rd-C68_S13 3rd-C69_S78 3rd-C6_S44 3rd-C71_S80
#> "024" "011321" "0121" "0124" "024" "011322" "01111"
#> 3rd-C76_S22 3rd-C79_S67 3rd-C7_S40 3rd-C82_S11 3rd-C84_S75 3rd-C85_S79 3rd-C85_S83
#> "0121" "01121" "024" "01111" "01111" "01121" "024"
#> 3rd-C86_S85 3rd-C87_S88 3rd-C88_S24 3rd-C91_S91 3rd-C92_S86 3rd-C95_S81 3rd-C96_S79
#> "0124" "01232" "01111" "01121" "01111" "01121" "0212"
#> 3rd-C9_S5 4th-61_S28 4th-C12_S19 4th-C14_S26 4th-C18_S31 4th-C22_S45 4th-C23_S44
#> "011322" "01111" "0121" "01111" "01122" "024" "0121"
#> 4th-C24_S43 4th-C26_S50 4th-C27_S51 4th-C28_S55 4th-C29_S56 4th-C32_S62 4th-C33_S63
#> "01112" "01111" "0233" "0124" "0121" "0124" "0121"
#> 4th-C35_S68 4th-C36_S69 4th-C37_S73 4th-C3_S1 4th-C40_S79 4th-C43_S85 4th-C45_S87
#> "024" "011322" "024" "024" "01121" "01231" "0212"
#> 4th-C49_S4 4th-C4_S9 4th-C50_S5 4th-C51_S6 4th-C56_S17 4th-C57_S18 4th-C59_S23
#> "0124" "01122" "024" "0121" "01122" "024" "0121"
#> 4th-C5_S8 4th-C62_S29 4th-C63_S30 4th-C64_S34 4th-C66_S36 4th-C67_S40 4th-C68_S41
#> "01112" "01121" "0121" "01121" "01121" "01131" "0222"
#> 4th-C69_S42 4th-C70_S46 4th-C73_S54 4th-C75_S52 4th-C78_S58 4th-C79_S66 4th-C7_S15
#> "0121" "01231" "01122" "01122" "01222" "01122" "01111"
#> 4th-C80_S65 4th-C81_S64 4th-C82_S72 4th-C83_S71 4th-C85_S78 4th-C86_S77 4th-C87_S76
#> "01121" "01221" "01121" "01122" "01112" "01121" "0124"
#> 4th-C88_S84 4th-C89_S83 4th-C8_S14 4th-C92_S89 4th-C93_S88 4th-C94_S96 4th-C95_S95
#> "01121" "01112" "0124" "01121" "0212" "01122" "01221"
#> 4th-C96_S94 4th-C9_S13 5th-C10_S92 5th-C11_S91 5th-C12_S90 5th-C14_S97 5th-C16_S98
#> "01122" "024" "0231" "0231" "01231" "0211" "0233"
#> 5th-C18_S96 5th-C19_S104 5th-C21_S102 5th-C25_S108 5th-C30_S105 5th-C34_S108 5th-C35_S109
#> "0211" "01221" "0121" "0233" "01221" "01121" "01131"
#> 5th-C40_S112 5th-C41_S113 5th-C42_S114 5th-C43_S121 5th-C45_S123 5th-C47_S118 5th-C49_S89
#> "0231" "0222" "0231" "0233" "0231" "01222" "01111"
#> 5th-C50_S90 5th-C54_S89 5th-C56_S95 5th-C57_S96 5th-C58_S93 5th-C59_S94 5th-C5_S85
#> "01221" "01221" "0231" "01223" "0231" "01223" "01111"
#> 5th-C64_S99 5th-C66_S101 5th-C67_S105 5th-C68_S106 5th-C69_S107 5th-C6_S84 5th-C70_S103
#> "01223" "01223" "0232" "01223" "01223" "024" "024"
#> 5th-C73_S111 5th-C74_S110 5th-C77_S107 5th-C7_S93 5th-C80_S116 5th-C81_S115 5th-C83_S111
#> "0231" "01223" "01223" "01111" "0212" "0231" "0222"
#> 5th-C87_S119 5th-C88_S117 5th-C90_S115 5th-C92_S124 5th-C9_S92 6th-C12_S18 6th-C15_S22
#> "024" "0231" "01131" "01223" "01121" "01111" "0211"
#> 6th-C16_S29 6th-C19_S35 6th-C1_S3 6th-C20_S34 6th-C21_S33 6th-C22_S39 6th-C23_S38
#> "0124" "0212" "0211" "01131" "01122" "01131" "01111"
#> 6th-C24_S37 6th-C25_S43 6th-C28_S49 6th-C29_S50 6th-C2_S2 6th-C30_S51 6th-C34_S61
#> "011321" "0212" "0212" "01112" "011321" "011321" "0221"
#> 6th-C40_S73 6th-C42_S75 6th-C45_S81 6th-C51_S6 6th-C53_S10 6th-C54_S11 6th-C57_S17
#> "01131" "01131" "0221" "011321" "01231" "01111" "0211"
#> 6th-C58_S20 6th-C59_S21 6th-C5_S8 6th-C62_S25 6th-C63_S26 6th-C64_S30 6th-C65_S31
#> "0211" "01111" "0121" "0212" "01111" "0211" "0121"
#> 6th-C66_S32 6th-C67_S36 6th-C71_S41 6th-C73_S48 6th-C75_S46 6th-C77_S53 6th-C79_S60
#> "01131" "0212" "01112" "011321" "011321" "01111" "01112"
#> 6th-C80_S59 6th-C82_S66 6th-C83_S65 6th-C84_S64 6th-C85_S72 6th-C87_S70 6th-C89_S77
#> "01131" "0211" "024" "0211" "01112" "01122" "0212"
#> 6th-C90_S76 6th-C91_S84 6th-C93_S82 6th-C9_S12 7th-C10_S19 7th-C11_S18 7th-C12_S17
#> "0211" "0124" "0124" "0221" "011321" "01122" "0212"
#> 7th-C14_S24 7th-C15_S23 7th-C17_S29 7th-C19_S36 7th-C1_S3 7th-C20_S35 7th-C21_S34
#> "01121" "0124" "01231" "0211" "0211" "0212" "0211"
#> 7th-C24_S40 7th-C25_S43 7th-C28_S48 7th-C2_S2 7th-C31_S53 7th-C32_S54 7th-C34_S59
#> "01121" "01111" "0212" "0212" "01131" "0121" "0121"
#> 7th-C36_S61 7th-C3_S1 7th-C40_S70 7th-C44_S76 7th-C45_S77 7th-C47_S81 7th-C49_S4
#> "01122" "0212" "01222" "01231" "01112" "0222" "0222"
#> 7th-C4_S8 7th-C50_S5 7th-C52_S9 7th-C53_S10 7th-C56_S15 7th-C57_S16 7th-C58_S20
#> "0212" "01131" "0212" "01111" "01231" "0212" "01121"
#> 7th-C59_S21 7th-C60_S22 7th-C62_S27 7th-C64_S31 7th-C65_S32 7th-C66_S33 7th-C68_S38
#> "01111" "0212" "01112" "01111" "0211" "01131" "01231"
#> 7th-C69_S39 7th-C72_S42 7th-C73_S47 7th-C76_S52 7th-C77_S51 7th-C79_S58 7th-C80_S57
#> "0121" "0124" "011321" "0232" "01111" "01122" "011321"
#> 7th-C81_S56 7th-C82_S64 7th-C84_S62 7th-C85_S69 7th-C88_S75 7th-C89_S74 7th-C8_S13
#> "0233" "01122" "01111" "0221" "01231" "01131" "01111"
#> 7th-C90_S73 7th-C94_S83 7th-C96_S82 8th-C10_S100 8th-C11_S99 8th-C18_S110 8th-C20_S116
#> "01111" "0211" "01111" "01111" "0121" "0222" "01232"
#> 8th-C21_S115 8th-C23_S121 8th-C24_S120 8th-C26_S126 8th-C28_S131 8th-C2_S85 8th-C34_S141
#> "0222" "024" "01112" "0221" "024" "01111" "0121"
#> 8th-C37_S146 8th-C38_S147 8th-C44_S155 8th-C47_S160 8th-C55_S96 8th-C57_S98 8th-C58_S101
#> "0222" "0211" "01131" "0211" "01122" "01122" "01121"
#> 8th-C59_S102 8th-C61_S107 8th-C64_S112 8th-C65_S113 8th-C67_S117 8th-C69_S119 8th-C6_S88
#> "0121" "0124" "0121" "01112" "01122" "0222" "01232"
#> 8th-C70_S123 8th-C73_S130 8th-C74_S129 8th-C75_S128 8th-C79_S140 8th-C7_S95 8th-C84_S143
#> "0211" "01221" "01122" "0211" "024" "0121" "0211"
#> 8th-C85_S150 8th-C87_S148 8th-C90_S152 8th-C91_S158 8th-C92_S157 8th-C94_S162 8th-C95_S161
#> "01122" "01112" "024" "0222" "01232" "024" "0121"
#> 9th-C10_S18 9th-C11_S17 9th-C13_S24 9th-C14_S23 9th-C15_S22 9th-C16_S30 9th-C17_S29
#> "01131" "01131" "0211" "0211" "0121" "0124" "0121"
#> 9th-C19_S36 9th-C1_S3 9th-C20_S35 9th-C22_S41 9th-C25_S45 9th-C28_S50 9th-C29_S51
#> "0121" "01131" "0222" "0233" "0211" "01232" "0121"
#> 9th-C2_S2 9th-C30_S52 9th-C36_S59 9th-C38_S64 9th-C3_S1 9th-C40_S69 9th-C41_S70
#> "0232" "0121" "01222" "01131" "01131" "01231" "01112"
#> 9th-C46_S79 9th-C49_S4 9th-C51_S6 9th-C52_S10 9th-C57_S16 9th-C59_S20 9th-C5_S8
#> "01131" "024" "0211" "024" "01122" "0212" "0121"
#> 9th-C61_S25 9th-C62_S26 9th-C64_S31 9th-C65_S32 9th-C66_S33 9th-C67_S37 9th-C69_S39
#> "01221" "0121" "0121" "0124" "01232" "0121" "0212"
#> 9th-C6_S7 9th-C70_S42 9th-C74_S48 9th-C75_S47 9th-C77_S53 9th-C79_S57 9th-C80_S56
#> "01131" "01112" "0121" "024" "0121" "024" "01122"
#> 9th-C81_S55 9th-C83_S61 9th-C84_S60 9th-C85_S68 9th-C86_S67 9th-C87_S66 9th-C88_S73
#> "01131" "01121" "01223" "0222" "01131" "0221" "0211"
#> 9th-C89_S72 9th-C8_S14 9th-C91_S78 9th-C92_S77 9th-C93_S76 9th-C94_S83 9th-C96_S81
#> "01131" "01131" "0212" "024" "01131" "0212" "01222"
#> 9th-C9_S13
#> "01122"
get_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 249))
#> 10th_C10_S104 10th_C11_S96 10th_C13_S61 10th_C14_S53 10th_C16_S105 10th_C17_S97 10th_C19_S62
#> "01231" "0211" "01112" "0124" "01231" "0211" "01132"
#> 10th_C1_S59 10th_C20_S54 10th_C23_S98 10th_C24_S90 10th_C28_S91 10th_C30_S107 10th_C31_S48
#> "0124" "0124" "01232" "01231" "0222" "0121" "0121"
#> 10th_C32_S56 10th_C33_S64 10th_C34_S92 10th_C37_S49 10th_C41_S101 10th_C42_S109 10th_C43_S50
#> "0211" "0211" "024" "0211" "01232" "0231" "0221"
#> 10th_C45_S66 10th_C46_S94 10th_C4_S103 10th_C50_S73 10th_C51_S80 10th_C52_S110 10th_C53_S118
#> "0121" "01222" "01221" "024" "0221" "024" "0221"
#> 10th_C54_S124 10th_C56_S74 10th_C57_S81 10th_C58_S111 10th_C5_S95 10th_C61_S68 10th_C63_S82
#> "01231" "01222" "0222" "0222" "0221" "0211" "0231"
#> 10th_C64_S112 10th_C66_S126 10th_C68_S75 10th_C6_S88 10th_C73_S84 10th_C74_S76 10th_C76_S128
#> "0211" "0211" "01231" "0222" "01221" "0121" "0124"
#> 10th_C77_S120 10th_C78_S114 10th_C7_S60 10th_C80_S77 10th_C81_S70 10th_C84_S115 10th_C85_S86
#> "0232" "0222" "01221" "0233" "01131" "01131" "0124"
#> 10th_C86_S78 10th_C87_S71 10th_C88_S130 10th_C8_S52 10th_C90_S116 10th_C95_S123 10th_C96_S117
#> "0231" "0231" "01221" "01232" "0121" "024" "0121"
#> 11th-C10_S63 11th-C12_S47 11th-C16_S64 11th-C21_S4 11th-C22_S65 11th-C24_S49 11th-C26_S12
#> "0222" "024" "01231" "0212" "0211" "01221" "0233"
#> 11th-C27_S19 11th-C2_S8 11th-C30_S66 11th-C33_S20 11th-C36_S67 11th-C37_S6 11th-C39_S21
#> "0212" "0232" "0222" "01231" "01232" "0221" "01232"
#> 11th-C40_S52 11th-C41_S60 11th-C43_S7 11th-C44_S15 11th-C49_S23 11th-C4_S62 11th-C51_S39
#> "01222" "01132" "0233" "01131" "01131" "0233" "01131"
#> 11th-C53_S78 11th-C54_S86 11th-C55_S24 11th-C56_S32 11th-C57_S40 11th-C58_S71 11th-C5_S54
#> "01131" "0212" "0233" "0232" "024" "01221" "0121"
#> 11th-C61_S25 11th-C62_S33 11th-C64_S72 11th-C66_S88 11th-C67_S26 11th-C68_S34 11th-C77_S82
#> "01232" "0222" "0231" "01112" "0221" "01221" "0232"
#> 11th-C7_S16 11th-C93_S30 12th-C10_S155 12th-C11_S147 12th-C12_S139 12th-C14_S190 12th-C15_S183
#> "01132" "0222" "0211" "0121" "0124" "01131" "0211"
#> 12th-C1_S195 12th-C20_S191 12th-C21_S184 12th-C23_S149 12th-C24_S141 12th-C25_S185 12th-C26_S192
#> "0221" "01232" "0211" "0221" "01131" "0124" "0124"
#> 12th-C28_S142 12th-C29_S150 12th-C30_S157 12th-C33_S200 12th-C35_S151 12th-C36_S158 12th-C37_S187
#> "0121" "01122" "0124" "0124" "0211" "0232" "0222"
#> 12th-C38_S194 12th-C39_S201 12th-C3_S181 12th-C40_S144 12th-C42_S159 12th-C46_S145 12th-C47_S153
#> "0211" "0221" "0211" "0221" "01131" "01222" "0211"
#> 12th-C48_S160 12th-C4_S154 12th-C50_S210 12th-C51_S217 12th-C53_S168 12th-C55_S203 12th-C56_S211
#> "0124" "0221" "024" "0124" "0231" "01132" "0233"
#> 12th-C57_S218 12th-C58_S162 12th-C59_S169 12th-C60_S176 12th-C63_S219 12th-C64_S163 12th-C65_S170
#> "024" "01121" "01112" "01112" "0121" "01112" "01131"
#> 12th-C67_S205 12th-C69_S135 12th-C71_S171 12th-C74_S214 12th-C75_S206 12th-C76_S177 12th-C7_S196
#> "0212" "01222" "0221" "01112" "0221" "01112" "01131"
#> 12th-C80_S215 12th-C81_S207 12th-C84_S165 12th-C85_S137 12th-C8_S189 12th-C90_S166 12th-C93_S209
#> "0121" "0121" "01112" "01232" "0221" "01131" "0212"
#> 12th-C94_S180 12th-C95_S174 12th-C96_S167 13th_C12_S178 13th_C13_S149 13th_C15_S134 13th_C16_S193
#> "01222" "01121" "01112" "0124" "0121" "0212" "0124"
#> 13th_C17_S186 13th_C18_S179 13th_C1_S147 13th_C20_S142 13th_C21_S135 13th_C23_S187 13th_C27_S151
#> "0222" "0222" "0221" "0221" "0222" "01222" "0231"
#> 13th_C29_S188 13th_C31_S137 13th_C34_S181 13th_C36_S196 13th_C38_S145 13th_C39_S153 13th_C3_S132
#> "0221" "0222" "01131" "0232" "0221" "0124" "0221"
#> 13th_C46_S183 13th_C49_S155 13th_C4_S191 13th_C51_S170 13th_C52_S198 13th_C53_S205 13th_C54_S212
#> "0221" "0233" "0221" "0222" "0222" "0221" "0221"
#> 13th_C55_S156 13th_C57_S171 13th_C5_S184 13th_C60_S213 13th_C63_S172 13th_C66_S214 13th_C68_S165
#> "0222" "0211" "0222" "0121" "0222" "01122" "0222"
#> 13th_C69_S173 13th_C6_S177 13th_C70_S201 13th_C71_S208 13th_C72_S215 13th_C75_S159 13th_C76_S216
#> "0222" "0221" "0222" "0222" "0232" "0211" "01122"
#> 13th_C77_S209 13th_C79_S174 13th_C80_S167 13th_C81_S160 13th_C86_S168 13th_C88_S218 13th_C89_S211
#> "0221" "0222" "0212" "0212" "0221" "0222" "0222"
#> 13th_C8_S140 13th_C92_S169 13th_C93_S162 13th_C94_S219 13th_C96_S204 1st-61_S27 1st-C11_S58
#> "0233" "0221" "0221" "0124" "0124" "01111" "01112"
#> 1st-C13_S19 1st-C15_S3 1st-C18_S51 1st-C19_S20 1st-C20_S12 1st-C21_S4 1st-C32_S14
#> "0212" "0222" "024" "01122" "024" "0121" "01132"
#> 1st-C34_S54 1st-C39_S23 1st-C42_S71 1st-C50_S33 1st-C51_S41 1st-C53_S74 1st-C56_S34
#> "01222" "0212" "01132" "01122" "024" "024" "01121"
#> 1st-C57_S42 1st-C58_S76 1st-C59_S77 1st-C62_S35 1st-C64_S79 1st-C68_S36 1st-C69_S44
#> "01122" "01111" "024" "024" "01112" "01121" "0124"
#> 1st-C71_S83 1st-C73_S45 1st-C74_S37 1st-C75_S29 1st-C77_S86 1st-C78_S85 1st-C79_S46
#> "0121" "01122" "024" "01122" "01132" "01122" "0212"
#> 1st-C80_S38 1st-C8_S10 1st-C90_S91 1st-C96_S94 2nd-C11_S20 2nd-C15_S25 2nd-C16_S33
#> "01121" "024" "01112" "0211" "01121" "01112" "01121"
#> 2nd-C17_S32 2nd-C19_S39 2nd-C1_S3 2nd-C21_S37 2nd-C25_S49 2nd-C26_S50 2nd-C27_S51
#> "01112" "0212" "0222" "01132" "01232" "01121" "0212"
#> 2nd-C28_S55 2nd-C29_S56 2nd-C2_S2 2nd-C31_S61 2nd-C32_S62 2nd-C36_S69 2nd-C37_S73
#> "024" "0121" "0232" "0121" "01112" "024" "0211"
#> 2nd-C38_S74 2nd-C39_S75 2nd-C3_S1 2nd-C47_S92 2nd-C49_S4 2nd-C4_S9 2nd-C51_S6
#> "01112" "01121" "024" "0121" "0211" "024" "0212"
#> 2nd-C52_S10 2nd-C54_S12 2nd-C57_S18 2nd-C58_S22 2nd-C5_S8 2nd-C62_S29 2nd-C67_S40
#> "0212" "01222" "0121" "024" "0212" "01111" "01122"
#> 2nd-C69_S42 2nd-C6_S7 2nd-C72_S48 2nd-C74_S53 2nd-C75_S52 2nd-C76_S60 2nd-C77_S59
#> "0222" "0121" "01112" "0121" "01121" "01232" "01122"
#> 2nd-C7_S15 2nd-C80_S65 2nd-C81_S64 2nd-C83_S71 2nd-C86_S77 2nd-C87_S76 2nd-C88_S84
#> "0212" "01121" "0124" "0121" "01132" "0211" "01112"
#> 2nd-C8_S14 2nd-C93_S88 2nd-C94_S96 2nd-C95_S95 3rd-C11_S58 3rd-C12_S68 3rd-C18_S80
#> "01122" "01112" "0222" "01132" "01111" "01122" "0121"
#> 3rd-C1_S39 3rd-C20_S22 3rd-C21_S11 3rd-C23_S94 3rd-C25_S15 3rd-C26_S28 3rd-C27_S49
#> "01232" "01231" "0121" "024" "0212" "0121" "01122"
#> 3rd-C32_S31 3rd-C33_S50 3rd-C35_S23 3rd-C36_S2 3rd-C3_S2 3rd-C40_S57 3rd-C42_S74
#> "024" "01111" "01132" "01111" "024" "0124" "01222"
#> 3rd-C44_S32 3rd-C46_S93 3rd-C47_S35 3rd-C49_S60 3rd-C4_S25 3rd-C51_S87 3rd-C52_S86
#> "024" "01232" "01122" "01122" "01111" "0232" "024"
#> 3rd-C53_S67 3rd-C56_S90 3rd-C57_S5 3rd-C58_S3 3rd-C59_S91 3rd-C60_S10 3rd-C61_S64
#> "01112" "0212" "01121" "01111" "01111" "0211" "024"
#> 3rd-C63_S54 3rd-C65_S20 3rd-C67_S69 3rd-C68_S13 3rd-C69_S78 3rd-C6_S44 3rd-C71_S80
#> "024" "01132" "0121" "0124" "024" "01132" "01111"
#> 3rd-C76_S22 3rd-C79_S67 3rd-C7_S40 3rd-C82_S11 3rd-C84_S75 3rd-C85_S79 3rd-C85_S83
#> "0121" "01121" "024" "01111" "01111" "01121" "024"
#> 3rd-C86_S85 3rd-C87_S88 3rd-C88_S24 3rd-C91_S91 3rd-C92_S86 3rd-C95_S81 3rd-C96_S79
#> "0124" "01232" "01111" "01121" "01111" "01121" "0212"
#> 3rd-C9_S5 4th-61_S28 4th-C12_S19 4th-C14_S26 4th-C18_S31 4th-C22_S45 4th-C23_S44
#> "01132" "01111" "0121" "01111" "01122" "024" "0121"
#> 4th-C24_S43 4th-C26_S50 4th-C27_S51 4th-C28_S55 4th-C29_S56 4th-C32_S62 4th-C33_S63
#> "01112" "01111" "0233" "0124" "0121" "0124" "0121"
#> 4th-C35_S68 4th-C36_S69 4th-C37_S73 4th-C3_S1 4th-C40_S79 4th-C43_S85 4th-C45_S87
#> "024" "01132" "024" "024" "01121" "01231" "0212"
#> 4th-C49_S4 4th-C4_S9 4th-C50_S5 4th-C51_S6 4th-C56_S17 4th-C57_S18 4th-C59_S23
#> "0124" "01122" "024" "0121" "01122" "024" "0121"
#> 4th-C5_S8 4th-C62_S29 4th-C63_S30 4th-C64_S34 4th-C66_S36 4th-C67_S40 4th-C68_S41
#> "01112" "01121" "0121" "01121" "01121" "01131" "0222"
#> 4th-C69_S42 4th-C70_S46 4th-C73_S54 4th-C75_S52 4th-C78_S58 4th-C79_S66 4th-C7_S15
#> "0121" "01231" "01122" "01122" "01222" "01122" "01111"
#> 4th-C80_S65 4th-C81_S64 4th-C82_S72 4th-C83_S71 4th-C85_S78 4th-C86_S77 4th-C87_S76
#> "01121" "01221" "01121" "01122" "01112" "01121" "0124"
#> 4th-C88_S84 4th-C89_S83 4th-C8_S14 4th-C92_S89 4th-C93_S88 4th-C94_S96 4th-C95_S95
#> "01121" "01112" "0124" "01121" "0212" "01122" "01221"
#> 4th-C96_S94 4th-C9_S13 5th-C10_S92 5th-C11_S91 5th-C12_S90 5th-C14_S97 5th-C16_S98
#> "01122" "024" "0231" "0231" "01231" "0211" "0233"
#> 5th-C18_S96 5th-C19_S104 5th-C21_S102 5th-C25_S108 5th-C30_S105 5th-C34_S108 5th-C35_S109
#> "0211" "01221" "0121" "0233" "01221" "01121" "01131"
#> 5th-C40_S112 5th-C41_S113 5th-C42_S114 5th-C43_S121 5th-C45_S123 5th-C47_S118 5th-C49_S89
#> "0231" "0222" "0231" "0233" "0231" "01222" "01111"
#> 5th-C50_S90 5th-C54_S89 5th-C56_S95 5th-C57_S96 5th-C58_S93 5th-C59_S94 5th-C5_S85
#> "01221" "01221" "0231" "01223" "0231" "01223" "01111"
#> 5th-C64_S99 5th-C66_S101 5th-C67_S105 5th-C68_S106 5th-C69_S107 5th-C6_S84 5th-C70_S103
#> "01223" "01223" "0232" "01223" "01223" "024" "024"
#> 5th-C73_S111 5th-C74_S110 5th-C77_S107 5th-C7_S93 5th-C80_S116 5th-C81_S115 5th-C83_S111
#> "0231" "01223" "01223" "01111" "0212" "0231" "0222"
#> 5th-C87_S119 5th-C88_S117 5th-C90_S115 5th-C92_S124 5th-C9_S92 6th-C12_S18 6th-C15_S22
#> "024" "0231" "01131" "01223" "01121" "01111" "0211"
#> 6th-C16_S29 6th-C19_S35 6th-C1_S3 6th-C20_S34 6th-C21_S33 6th-C22_S39 6th-C23_S38
#> "0124" "0212" "0211" "01131" "01122" "01131" "01111"
#> 6th-C24_S37 6th-C25_S43 6th-C28_S49 6th-C29_S50 6th-C2_S2 6th-C30_S51 6th-C34_S61
#> "01132" "0212" "0212" "01112" "01132" "01132" "0221"
#> 6th-C40_S73 6th-C42_S75 6th-C45_S81 6th-C51_S6 6th-C53_S10 6th-C54_S11 6th-C57_S17
#> "01131" "01131" "0221" "01132" "01231" "01111" "0211"
#> 6th-C58_S20 6th-C59_S21 6th-C5_S8 6th-C62_S25 6th-C63_S26 6th-C64_S30 6th-C65_S31
#> "0211" "01111" "0121" "0212" "01111" "0211" "0121"
#> 6th-C66_S32 6th-C67_S36 6th-C71_S41 6th-C73_S48 6th-C75_S46 6th-C77_S53 6th-C79_S60
#> "01131" "0212" "01112" "01132" "01132" "01111" "01112"
#> 6th-C80_S59 6th-C82_S66 6th-C83_S65 6th-C84_S64 6th-C85_S72 6th-C87_S70 6th-C89_S77
#> "01131" "0211" "024" "0211" "01112" "01122" "0212"
#> 6th-C90_S76 6th-C91_S84 6th-C93_S82 6th-C9_S12 7th-C10_S19 7th-C11_S18 7th-C12_S17
#> "0211" "0124" "0124" "0221" "01132" "01122" "0212"
#> 7th-C14_S24 7th-C15_S23 7th-C17_S29 7th-C19_S36 7th-C1_S3 7th-C20_S35 7th-C21_S34
#> "01121" "0124" "01231" "0211" "0211" "0212" "0211"
#> 7th-C24_S40 7th-C25_S43 7th-C28_S48 7th-C2_S2 7th-C31_S53 7th-C32_S54 7th-C34_S59
#> "01121" "01111" "0212" "0212" "01131" "0121" "0121"
#> 7th-C36_S61 7th-C3_S1 7th-C40_S70 7th-C44_S76 7th-C45_S77 7th-C47_S81 7th-C49_S4
#> "01122" "0212" "01222" "01231" "01112" "0222" "0222"
#> 7th-C4_S8 7th-C50_S5 7th-C52_S9 7th-C53_S10 7th-C56_S15 7th-C57_S16 7th-C58_S20
#> "0212" "01131" "0212" "01111" "01231" "0212" "01121"
#> 7th-C59_S21 7th-C60_S22 7th-C62_S27 7th-C64_S31 7th-C65_S32 7th-C66_S33 7th-C68_S38
#> "01111" "0212" "01112" "01111" "0211" "01131" "01231"
#> 7th-C69_S39 7th-C72_S42 7th-C73_S47 7th-C76_S52 7th-C77_S51 7th-C79_S58 7th-C80_S57
#> "0121" "0124" "01132" "0232" "01111" "01122" "01132"
#> 7th-C81_S56 7th-C82_S64 7th-C84_S62 7th-C85_S69 7th-C88_S75 7th-C89_S74 7th-C8_S13
#> "0233" "01122" "01111" "0221" "01231" "01131" "01111"
#> 7th-C90_S73 7th-C94_S83 7th-C96_S82 8th-C10_S100 8th-C11_S99 8th-C18_S110 8th-C20_S116
#> "01111" "0211" "01111" "01111" "0121" "0222" "01232"
#> 8th-C21_S115 8th-C23_S121 8th-C24_S120 8th-C26_S126 8th-C28_S131 8th-C2_S85 8th-C34_S141
#> "0222" "024" "01112" "0221" "024" "01111" "0121"
#> 8th-C37_S146 8th-C38_S147 8th-C44_S155 8th-C47_S160 8th-C55_S96 8th-C57_S98 8th-C58_S101
#> "0222" "0211" "01131" "0211" "01122" "01122" "01121"
#> 8th-C59_S102 8th-C61_S107 8th-C64_S112 8th-C65_S113 8th-C67_S117 8th-C69_S119 8th-C6_S88
#> "0121" "0124" "0121" "01112" "01122" "0222" "01232"
#> 8th-C70_S123 8th-C73_S130 8th-C74_S129 8th-C75_S128 8th-C79_S140 8th-C7_S95 8th-C84_S143
#> "0211" "01221" "01122" "0211" "024" "0121" "0211"
#> 8th-C85_S150 8th-C87_S148 8th-C90_S152 8th-C91_S158 8th-C92_S157 8th-C94_S162 8th-C95_S161
#> "01122" "01112" "024" "0222" "01232" "024" "0121"
#> 9th-C10_S18 9th-C11_S17 9th-C13_S24 9th-C14_S23 9th-C15_S22 9th-C16_S30 9th-C17_S29
#> "01131" "01131" "0211" "0211" "0121" "0124" "0121"
#> 9th-C19_S36 9th-C1_S3 9th-C20_S35 9th-C22_S41 9th-C25_S45 9th-C28_S50 9th-C29_S51
#> "0121" "01131" "0222" "0233" "0211" "01232" "0121"
#> 9th-C2_S2 9th-C30_S52 9th-C36_S59 9th-C38_S64 9th-C3_S1 9th-C40_S69 9th-C41_S70
#> "0232" "0121" "01222" "01131" "01131" "01231" "01112"
#> 9th-C46_S79 9th-C49_S4 9th-C51_S6 9th-C52_S10 9th-C57_S16 9th-C59_S20 9th-C5_S8
#> "01131" "024" "0211" "024" "01122" "0212" "0121"
#> 9th-C61_S25 9th-C62_S26 9th-C64_S31 9th-C65_S32 9th-C66_S33 9th-C67_S37 9th-C69_S39
#> "01221" "0121" "0121" "0124" "01232" "0121" "0212"
#> 9th-C6_S7 9th-C70_S42 9th-C74_S48 9th-C75_S47 9th-C77_S53 9th-C79_S57 9th-C80_S56
#> "01131" "01112" "0121" "024" "0121" "024" "01122"
#> 9th-C81_S55 9th-C83_S61 9th-C84_S60 9th-C85_S68 9th-C86_S67 9th-C87_S66 9th-C88_S73
#> "01131" "01121" "01223" "0222" "01131" "0221" "0211"
#> 9th-C89_S72 9th-C8_S14 9th-C91_S78 9th-C92_S77 9th-C93_S76 9th-C94_S83 9th-C96_S81
#> "01131" "01131" "0212" "024" "01131" "0212" "01222"
#> 9th-C9_S13
#> "01122"
get_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 256))
#> 10th_C10_S104 10th_C11_S96 10th_C13_S61 10th_C14_S53 10th_C16_S105 10th_C17_S97 10th_C19_S62
#> "01231" "0211" "01112" "0124" "01231" "0211" "0113"
#> 10th_C1_S59 10th_C20_S54 10th_C23_S98 10th_C24_S90 10th_C28_S91 10th_C30_S107 10th_C31_S48
#> "0124" "0124" "01232" "01231" "0222" "0121" "0121"
#> 10th_C32_S56 10th_C33_S64 10th_C34_S92 10th_C37_S49 10th_C41_S101 10th_C42_S109 10th_C43_S50
#> "0211" "0211" "024" "0211" "01232" "0231" "0221"
#> 10th_C45_S66 10th_C46_S94 10th_C4_S103 10th_C50_S73 10th_C51_S80 10th_C52_S110 10th_C53_S118
#> "0121" "01222" "01221" "024" "0221" "024" "0221"
#> 10th_C54_S124 10th_C56_S74 10th_C57_S81 10th_C58_S111 10th_C5_S95 10th_C61_S68 10th_C63_S82
#> "01231" "01222" "0222" "0222" "0221" "0211" "0231"
#> 10th_C64_S112 10th_C66_S126 10th_C68_S75 10th_C6_S88 10th_C73_S84 10th_C74_S76 10th_C76_S128
#> "0211" "0211" "01231" "0222" "01221" "0121" "0124"
#> 10th_C77_S120 10th_C78_S114 10th_C7_S60 10th_C80_S77 10th_C81_S70 10th_C84_S115 10th_C85_S86
#> "0232" "0222" "01221" "0233" "0113" "0113" "0124"
#> 10th_C86_S78 10th_C87_S71 10th_C88_S130 10th_C8_S52 10th_C90_S116 10th_C95_S123 10th_C96_S117
#> "0231" "0231" "01221" "01232" "0121" "024" "0121"
#> 11th-C10_S63 11th-C12_S47 11th-C16_S64 11th-C21_S4 11th-C22_S65 11th-C24_S49 11th-C26_S12
#> "0222" "024" "01231" "0212" "0211" "01221" "0233"
#> 11th-C27_S19 11th-C2_S8 11th-C30_S66 11th-C33_S20 11th-C36_S67 11th-C37_S6 11th-C39_S21
#> "0212" "0232" "0222" "01231" "01232" "0221" "01232"
#> 11th-C40_S52 11th-C41_S60 11th-C43_S7 11th-C44_S15 11th-C49_S23 11th-C4_S62 11th-C51_S39
#> "01222" "0113" "0233" "0113" "0113" "0233" "0113"
#> 11th-C53_S78 11th-C54_S86 11th-C55_S24 11th-C56_S32 11th-C57_S40 11th-C58_S71 11th-C5_S54
#> "0113" "0212" "0233" "0232" "024" "01221" "0121"
#> 11th-C61_S25 11th-C62_S33 11th-C64_S72 11th-C66_S88 11th-C67_S26 11th-C68_S34 11th-C77_S82
#> "01232" "0222" "0231" "01112" "0221" "01221" "0232"
#> 11th-C7_S16 11th-C93_S30 12th-C10_S155 12th-C11_S147 12th-C12_S139 12th-C14_S190 12th-C15_S183
#> "0113" "0222" "0211" "0121" "0124" "0113" "0211"
#> 12th-C1_S195 12th-C20_S191 12th-C21_S184 12th-C23_S149 12th-C24_S141 12th-C25_S185 12th-C26_S192
#> "0221" "01232" "0211" "0221" "0113" "0124" "0124"
#> 12th-C28_S142 12th-C29_S150 12th-C30_S157 12th-C33_S200 12th-C35_S151 12th-C36_S158 12th-C37_S187
#> "0121" "01122" "0124" "0124" "0211" "0232" "0222"
#> 12th-C38_S194 12th-C39_S201 12th-C3_S181 12th-C40_S144 12th-C42_S159 12th-C46_S145 12th-C47_S153
#> "0211" "0221" "0211" "0221" "0113" "01222" "0211"
#> 12th-C48_S160 12th-C4_S154 12th-C50_S210 12th-C51_S217 12th-C53_S168 12th-C55_S203 12th-C56_S211
#> "0124" "0221" "024" "0124" "0231" "0113" "0233"
#> 12th-C57_S218 12th-C58_S162 12th-C59_S169 12th-C60_S176 12th-C63_S219 12th-C64_S163 12th-C65_S170
#> "024" "01121" "01112" "01112" "0121" "01112" "0113"
#> 12th-C67_S205 12th-C69_S135 12th-C71_S171 12th-C74_S214 12th-C75_S206 12th-C76_S177 12th-C7_S196
#> "0212" "01222" "0221" "01112" "0221" "01112" "0113"
#> 12th-C80_S215 12th-C81_S207 12th-C84_S165 12th-C85_S137 12th-C8_S189 12th-C90_S166 12th-C93_S209
#> "0121" "0121" "01112" "01232" "0221" "0113" "0212"
#> 12th-C94_S180 12th-C95_S174 12th-C96_S167 13th_C12_S178 13th_C13_S149 13th_C15_S134 13th_C16_S193
#> "01222" "01121" "01112" "0124" "0121" "0212" "0124"
#> 13th_C17_S186 13th_C18_S179 13th_C1_S147 13th_C20_S142 13th_C21_S135 13th_C23_S187 13th_C27_S151
#> "0222" "0222" "0221" "0221" "0222" "01222" "0231"
#> 13th_C29_S188 13th_C31_S137 13th_C34_S181 13th_C36_S196 13th_C38_S145 13th_C39_S153 13th_C3_S132
#> "0221" "0222" "0113" "0232" "0221" "0124" "0221"
#> 13th_C46_S183 13th_C49_S155 13th_C4_S191 13th_C51_S170 13th_C52_S198 13th_C53_S205 13th_C54_S212
#> "0221" "0233" "0221" "0222" "0222" "0221" "0221"
#> 13th_C55_S156 13th_C57_S171 13th_C5_S184 13th_C60_S213 13th_C63_S172 13th_C66_S214 13th_C68_S165
#> "0222" "0211" "0222" "0121" "0222" "01122" "0222"
#> 13th_C69_S173 13th_C6_S177 13th_C70_S201 13th_C71_S208 13th_C72_S215 13th_C75_S159 13th_C76_S216
#> "0222" "0221" "0222" "0222" "0232" "0211" "01122"
#> 13th_C77_S209 13th_C79_S174 13th_C80_S167 13th_C81_S160 13th_C86_S168 13th_C88_S218 13th_C89_S211
#> "0221" "0222" "0212" "0212" "0221" "0222" "0222"
#> 13th_C8_S140 13th_C92_S169 13th_C93_S162 13th_C94_S219 13th_C96_S204 1st-61_S27 1st-C11_S58
#> "0233" "0221" "0221" "0124" "0124" "01111" "01112"
#> 1st-C13_S19 1st-C15_S3 1st-C18_S51 1st-C19_S20 1st-C20_S12 1st-C21_S4 1st-C32_S14
#> "0212" "0222" "024" "01122" "024" "0121" "0113"
#> 1st-C34_S54 1st-C39_S23 1st-C42_S71 1st-C50_S33 1st-C51_S41 1st-C53_S74 1st-C56_S34
#> "01222" "0212" "0113" "01122" "024" "024" "01121"
#> 1st-C57_S42 1st-C58_S76 1st-C59_S77 1st-C62_S35 1st-C64_S79 1st-C68_S36 1st-C69_S44
#> "01122" "01111" "024" "024" "01112" "01121" "0124"
#> 1st-C71_S83 1st-C73_S45 1st-C74_S37 1st-C75_S29 1st-C77_S86 1st-C78_S85 1st-C79_S46
#> "0121" "01122" "024" "01122" "0113" "01122" "0212"
#> 1st-C80_S38 1st-C8_S10 1st-C90_S91 1st-C96_S94 2nd-C11_S20 2nd-C15_S25 2nd-C16_S33
#> "01121" "024" "01112" "0211" "01121" "01112" "01121"
#> 2nd-C17_S32 2nd-C19_S39 2nd-C1_S3 2nd-C21_S37 2nd-C25_S49 2nd-C26_S50 2nd-C27_S51
#> "01112" "0212" "0222" "0113" "01232" "01121" "0212"
#> 2nd-C28_S55 2nd-C29_S56 2nd-C2_S2 2nd-C31_S61 2nd-C32_S62 2nd-C36_S69 2nd-C37_S73
#> "024" "0121" "0232" "0121" "01112" "024" "0211"
#> 2nd-C38_S74 2nd-C39_S75 2nd-C3_S1 2nd-C47_S92 2nd-C49_S4 2nd-C4_S9 2nd-C51_S6
#> "01112" "01121" "024" "0121" "0211" "024" "0212"
#> 2nd-C52_S10 2nd-C54_S12 2nd-C57_S18 2nd-C58_S22 2nd-C5_S8 2nd-C62_S29 2nd-C67_S40
#> "0212" "01222" "0121" "024" "0212" "01111" "01122"
#> 2nd-C69_S42 2nd-C6_S7 2nd-C72_S48 2nd-C74_S53 2nd-C75_S52 2nd-C76_S60 2nd-C77_S59
#> "0222" "0121" "01112" "0121" "01121" "01232" "01122"
#> 2nd-C7_S15 2nd-C80_S65 2nd-C81_S64 2nd-C83_S71 2nd-C86_S77 2nd-C87_S76 2nd-C88_S84
#> "0212" "01121" "0124" "0121" "0113" "0211" "01112"
#> 2nd-C8_S14 2nd-C93_S88 2nd-C94_S96 2nd-C95_S95 3rd-C11_S58 3rd-C12_S68 3rd-C18_S80
#> "01122" "01112" "0222" "0113" "01111" "01122" "0121"
#> 3rd-C1_S39 3rd-C20_S22 3rd-C21_S11 3rd-C23_S94 3rd-C25_S15 3rd-C26_S28 3rd-C27_S49
#> "01232" "01231" "0121" "024" "0212" "0121" "01122"
#> 3rd-C32_S31 3rd-C33_S50 3rd-C35_S23 3rd-C36_S2 3rd-C3_S2 3rd-C40_S57 3rd-C42_S74
#> "024" "01111" "0113" "01111" "024" "0124" "01222"
#> 3rd-C44_S32 3rd-C46_S93 3rd-C47_S35 3rd-C49_S60 3rd-C4_S25 3rd-C51_S87 3rd-C52_S86
#> "024" "01232" "01122" "01122" "01111" "0232" "024"
#> 3rd-C53_S67 3rd-C56_S90 3rd-C57_S5 3rd-C58_S3 3rd-C59_S91 3rd-C60_S10 3rd-C61_S64
#> "01112" "0212" "01121" "01111" "01111" "0211" "024"
#> 3rd-C63_S54 3rd-C65_S20 3rd-C67_S69 3rd-C68_S13 3rd-C69_S78 3rd-C6_S44 3rd-C71_S80
#> "024" "0113" "0121" "0124" "024" "0113" "01111"
#> 3rd-C76_S22 3rd-C79_S67 3rd-C7_S40 3rd-C82_S11 3rd-C84_S75 3rd-C85_S79 3rd-C85_S83
#> "0121" "01121" "024" "01111" "01111" "01121" "024"
#> 3rd-C86_S85 3rd-C87_S88 3rd-C88_S24 3rd-C91_S91 3rd-C92_S86 3rd-C95_S81 3rd-C96_S79
#> "0124" "01232" "01111" "01121" "01111" "01121" "0212"
#> 3rd-C9_S5 4th-61_S28 4th-C12_S19 4th-C14_S26 4th-C18_S31 4th-C22_S45 4th-C23_S44
#> "0113" "01111" "0121" "01111" "01122" "024" "0121"
#> 4th-C24_S43 4th-C26_S50 4th-C27_S51 4th-C28_S55 4th-C29_S56 4th-C32_S62 4th-C33_S63
#> "01112" "01111" "0233" "0124" "0121" "0124" "0121"
#> 4th-C35_S68 4th-C36_S69 4th-C37_S73 4th-C3_S1 4th-C40_S79 4th-C43_S85 4th-C45_S87
#> "024" "0113" "024" "024" "01121" "01231" "0212"
#> 4th-C49_S4 4th-C4_S9 4th-C50_S5 4th-C51_S6 4th-C56_S17 4th-C57_S18 4th-C59_S23
#> "0124" "01122" "024" "0121" "01122" "024" "0121"
#> 4th-C5_S8 4th-C62_S29 4th-C63_S30 4th-C64_S34 4th-C66_S36 4th-C67_S40 4th-C68_S41
#> "01112" "01121" "0121" "01121" "01121" "0113" "0222"
#> 4th-C69_S42 4th-C70_S46 4th-C73_S54 4th-C75_S52 4th-C78_S58 4th-C79_S66 4th-C7_S15
#> "0121" "01231" "01122" "01122" "01222" "01122" "01111"
#> 4th-C80_S65 4th-C81_S64 4th-C82_S72 4th-C83_S71 4th-C85_S78 4th-C86_S77 4th-C87_S76
#> "01121" "01221" "01121" "01122" "01112" "01121" "0124"
#> 4th-C88_S84 4th-C89_S83 4th-C8_S14 4th-C92_S89 4th-C93_S88 4th-C94_S96 4th-C95_S95
#> "01121" "01112" "0124" "01121" "0212" "01122" "01221"
#> 4th-C96_S94 4th-C9_S13 5th-C10_S92 5th-C11_S91 5th-C12_S90 5th-C14_S97 5th-C16_S98
#> "01122" "024" "0231" "0231" "01231" "0211" "0233"
#> 5th-C18_S96 5th-C19_S104 5th-C21_S102 5th-C25_S108 5th-C30_S105 5th-C34_S108 5th-C35_S109
#> "0211" "01221" "0121" "0233" "01221" "01121" "0113"
#> 5th-C40_S112 5th-C41_S113 5th-C42_S114 5th-C43_S121 5th-C45_S123 5th-C47_S118 5th-C49_S89
#> "0231" "0222" "0231" "0233" "0231" "01222" "01111"
#> 5th-C50_S90 5th-C54_S89 5th-C56_S95 5th-C57_S96 5th-C58_S93 5th-C59_S94 5th-C5_S85
#> "01221" "01221" "0231" "01223" "0231" "01223" "01111"
#> 5th-C64_S99 5th-C66_S101 5th-C67_S105 5th-C68_S106 5th-C69_S107 5th-C6_S84 5th-C70_S103
#> "01223" "01223" "0232" "01223" "01223" "024" "024"
#> 5th-C73_S111 5th-C74_S110 5th-C77_S107 5th-C7_S93 5th-C80_S116 5th-C81_S115 5th-C83_S111
#> "0231" "01223" "01223" "01111" "0212" "0231" "0222"
#> 5th-C87_S119 5th-C88_S117 5th-C90_S115 5th-C92_S124 5th-C9_S92 6th-C12_S18 6th-C15_S22
#> "024" "0231" "0113" "01223" "01121" "01111" "0211"
#> 6th-C16_S29 6th-C19_S35 6th-C1_S3 6th-C20_S34 6th-C21_S33 6th-C22_S39 6th-C23_S38
#> "0124" "0212" "0211" "0113" "01122" "0113" "01111"
#> 6th-C24_S37 6th-C25_S43 6th-C28_S49 6th-C29_S50 6th-C2_S2 6th-C30_S51 6th-C34_S61
#> "0113" "0212" "0212" "01112" "0113" "0113" "0221"
#> 6th-C40_S73 6th-C42_S75 6th-C45_S81 6th-C51_S6 6th-C53_S10 6th-C54_S11 6th-C57_S17
#> "0113" "0113" "0221" "0113" "01231" "01111" "0211"
#> 6th-C58_S20 6th-C59_S21 6th-C5_S8 6th-C62_S25 6th-C63_S26 6th-C64_S30 6th-C65_S31
#> "0211" "01111" "0121" "0212" "01111" "0211" "0121"
#> 6th-C66_S32 6th-C67_S36 6th-C71_S41 6th-C73_S48 6th-C75_S46 6th-C77_S53 6th-C79_S60
#> "0113" "0212" "01112" "0113" "0113" "01111" "01112"
#> 6th-C80_S59 6th-C82_S66 6th-C83_S65 6th-C84_S64 6th-C85_S72 6th-C87_S70 6th-C89_S77
#> "0113" "0211" "024" "0211" "01112" "01122" "0212"
#> 6th-C90_S76 6th-C91_S84 6th-C93_S82 6th-C9_S12 7th-C10_S19 7th-C11_S18 7th-C12_S17
#> "0211" "0124" "0124" "0221" "0113" "01122" "0212"
#> 7th-C14_S24 7th-C15_S23 7th-C17_S29 7th-C19_S36 7th-C1_S3 7th-C20_S35 7th-C21_S34
#> "01121" "0124" "01231" "0211" "0211" "0212" "0211"
#> 7th-C24_S40 7th-C25_S43 7th-C28_S48 7th-C2_S2 7th-C31_S53 7th-C32_S54 7th-C34_S59
#> "01121" "01111" "0212" "0212" "0113" "0121" "0121"
#> 7th-C36_S61 7th-C3_S1 7th-C40_S70 7th-C44_S76 7th-C45_S77 7th-C47_S81 7th-C49_S4
#> "01122" "0212" "01222" "01231" "01112" "0222" "0222"
#> 7th-C4_S8 7th-C50_S5 7th-C52_S9 7th-C53_S10 7th-C56_S15 7th-C57_S16 7th-C58_S20
#> "0212" "0113" "0212" "01111" "01231" "0212" "01121"
#> 7th-C59_S21 7th-C60_S22 7th-C62_S27 7th-C64_S31 7th-C65_S32 7th-C66_S33 7th-C68_S38
#> "01111" "0212" "01112" "01111" "0211" "0113" "01231"
#> 7th-C69_S39 7th-C72_S42 7th-C73_S47 7th-C76_S52 7th-C77_S51 7th-C79_S58 7th-C80_S57
#> "0121" "0124" "0113" "0232" "01111" "01122" "0113"
#> 7th-C81_S56 7th-C82_S64 7th-C84_S62 7th-C85_S69 7th-C88_S75 7th-C89_S74 7th-C8_S13
#> "0233" "01122" "01111" "0221" "01231" "0113" "01111"
#> 7th-C90_S73 7th-C94_S83 7th-C96_S82 8th-C10_S100 8th-C11_S99 8th-C18_S110 8th-C20_S116
#> "01111" "0211" "01111" "01111" "0121" "0222" "01232"
#> 8th-C21_S115 8th-C23_S121 8th-C24_S120 8th-C26_S126 8th-C28_S131 8th-C2_S85 8th-C34_S141
#> "0222" "024" "01112" "0221" "024" "01111" "0121"
#> 8th-C37_S146 8th-C38_S147 8th-C44_S155 8th-C47_S160 8th-C55_S96 8th-C57_S98 8th-C58_S101
#> "0222" "0211" "0113" "0211" "01122" "01122" "01121"
#> 8th-C59_S102 8th-C61_S107 8th-C64_S112 8th-C65_S113 8th-C67_S117 8th-C69_S119 8th-C6_S88
#> "0121" "0124" "0121" "01112" "01122" "0222" "01232"
#> 8th-C70_S123 8th-C73_S130 8th-C74_S129 8th-C75_S128 8th-C79_S140 8th-C7_S95 8th-C84_S143
#> "0211" "01221" "01122" "0211" "024" "0121" "0211"
#> 8th-C85_S150 8th-C87_S148 8th-C90_S152 8th-C91_S158 8th-C92_S157 8th-C94_S162 8th-C95_S161
#> "01122" "01112" "024" "0222" "01232" "024" "0121"
#> 9th-C10_S18 9th-C11_S17 9th-C13_S24 9th-C14_S23 9th-C15_S22 9th-C16_S30 9th-C17_S29
#> "0113" "0113" "0211" "0211" "0121" "0124" "0121"
#> 9th-C19_S36 9th-C1_S3 9th-C20_S35 9th-C22_S41 9th-C25_S45 9th-C28_S50 9th-C29_S51
#> "0121" "0113" "0222" "0233" "0211" "01232" "0121"
#> 9th-C2_S2 9th-C30_S52 9th-C36_S59 9th-C38_S64 9th-C3_S1 9th-C40_S69 9th-C41_S70
#> "0232" "0121" "01222" "0113" "0113" "01231" "01112"
#> 9th-C46_S79 9th-C49_S4 9th-C51_S6 9th-C52_S10 9th-C57_S16 9th-C59_S20 9th-C5_S8
#> "0113" "024" "0211" "024" "01122" "0212" "0121"
#> 9th-C61_S25 9th-C62_S26 9th-C64_S31 9th-C65_S32 9th-C66_S33 9th-C67_S37 9th-C69_S39
#> "01221" "0121" "0121" "0124" "01232" "0121" "0212"
#> 9th-C6_S7 9th-C70_S42 9th-C74_S48 9th-C75_S47 9th-C77_S53 9th-C79_S57 9th-C80_S56
#> "0113" "01112" "0121" "024" "0121" "024" "01122"
#> 9th-C81_S55 9th-C83_S61 9th-C84_S60 9th-C85_S68 9th-C86_S67 9th-C87_S66 9th-C88_S73
#> "0113" "01121" "01223" "0222" "0113" "0221" "0211"
#> 9th-C89_S72 9th-C8_S14 9th-C91_S78 9th-C92_S77 9th-C93_S76 9th-C94_S83 9th-C96_S81
#> "0113" "0113" "0212" "024" "0113" "0212" "01222"
#> 9th-C9_S13
#> "01122"
get_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 373))
#> 10th_C10_S104 10th_C11_S96 10th_C13_S61 10th_C14_S53 10th_C16_S105 10th_C17_S97 10th_C19_S62
#> "01231" "0211" "0111" "0124" "01231" "0211" "0113"
#> 10th_C1_S59 10th_C20_S54 10th_C23_S98 10th_C24_S90 10th_C28_S91 10th_C30_S107 10th_C31_S48
#> "0124" "0124" "01232" "01231" "0222" "0121" "0121"
#> 10th_C32_S56 10th_C33_S64 10th_C34_S92 10th_C37_S49 10th_C41_S101 10th_C42_S109 10th_C43_S50
#> "0211" "0211" "024" "0211" "01232" "0231" "0221"
#> 10th_C45_S66 10th_C46_S94 10th_C4_S103 10th_C50_S73 10th_C51_S80 10th_C52_S110 10th_C53_S118
#> "0121" "01222" "01221" "024" "0221" "024" "0221"
#> 10th_C54_S124 10th_C56_S74 10th_C57_S81 10th_C58_S111 10th_C5_S95 10th_C61_S68 10th_C63_S82
#> "01231" "01222" "0222" "0222" "0221" "0211" "0231"
#> 10th_C64_S112 10th_C66_S126 10th_C68_S75 10th_C6_S88 10th_C73_S84 10th_C74_S76 10th_C76_S128
#> "0211" "0211" "01231" "0222" "01221" "0121" "0124"
#> 10th_C77_S120 10th_C78_S114 10th_C7_S60 10th_C80_S77 10th_C81_S70 10th_C84_S115 10th_C85_S86
#> "0232" "0222" "01221" "0233" "0113" "0113" "0124"
#> 10th_C86_S78 10th_C87_S71 10th_C88_S130 10th_C8_S52 10th_C90_S116 10th_C95_S123 10th_C96_S117
#> "0231" "0231" "01221" "01232" "0121" "024" "0121"
#> 11th-C10_S63 11th-C12_S47 11th-C16_S64 11th-C21_S4 11th-C22_S65 11th-C24_S49 11th-C26_S12
#> "0222" "024" "01231" "0212" "0211" "01221" "0233"
#> 11th-C27_S19 11th-C2_S8 11th-C30_S66 11th-C33_S20 11th-C36_S67 11th-C37_S6 11th-C39_S21
#> "0212" "0232" "0222" "01231" "01232" "0221" "01232"
#> 11th-C40_S52 11th-C41_S60 11th-C43_S7 11th-C44_S15 11th-C49_S23 11th-C4_S62 11th-C51_S39
#> "01222" "0113" "0233" "0113" "0113" "0233" "0113"
#> 11th-C53_S78 11th-C54_S86 11th-C55_S24 11th-C56_S32 11th-C57_S40 11th-C58_S71 11th-C5_S54
#> "0113" "0212" "0233" "0232" "024" "01221" "0121"
#> 11th-C61_S25 11th-C62_S33 11th-C64_S72 11th-C66_S88 11th-C67_S26 11th-C68_S34 11th-C77_S82
#> "01232" "0222" "0231" "0111" "0221" "01221" "0232"
#> 11th-C7_S16 11th-C93_S30 12th-C10_S155 12th-C11_S147 12th-C12_S139 12th-C14_S190 12th-C15_S183
#> "0113" "0222" "0211" "0121" "0124" "0113" "0211"
#> 12th-C1_S195 12th-C20_S191 12th-C21_S184 12th-C23_S149 12th-C24_S141 12th-C25_S185 12th-C26_S192
#> "0221" "01232" "0211" "0221" "0113" "0124" "0124"
#> 12th-C28_S142 12th-C29_S150 12th-C30_S157 12th-C33_S200 12th-C35_S151 12th-C36_S158 12th-C37_S187
#> "0121" "01122" "0124" "0124" "0211" "0232" "0222"
#> 12th-C38_S194 12th-C39_S201 12th-C3_S181 12th-C40_S144 12th-C42_S159 12th-C46_S145 12th-C47_S153
#> "0211" "0221" "0211" "0221" "0113" "01222" "0211"
#> 12th-C48_S160 12th-C4_S154 12th-C50_S210 12th-C51_S217 12th-C53_S168 12th-C55_S203 12th-C56_S211
#> "0124" "0221" "024" "0124" "0231" "0113" "0233"
#> 12th-C57_S218 12th-C58_S162 12th-C59_S169 12th-C60_S176 12th-C63_S219 12th-C64_S163 12th-C65_S170
#> "024" "01121" "0111" "0111" "0121" "0111" "0113"
#> 12th-C67_S205 12th-C69_S135 12th-C71_S171 12th-C74_S214 12th-C75_S206 12th-C76_S177 12th-C7_S196
#> "0212" "01222" "0221" "0111" "0221" "0111" "0113"
#> 12th-C80_S215 12th-C81_S207 12th-C84_S165 12th-C85_S137 12th-C8_S189 12th-C90_S166 12th-C93_S209
#> "0121" "0121" "0111" "01232" "0221" "0113" "0212"
#> 12th-C94_S180 12th-C95_S174 12th-C96_S167 13th_C12_S178 13th_C13_S149 13th_C15_S134 13th_C16_S193
#> "01222" "01121" "0111" "0124" "0121" "0212" "0124"
#> 13th_C17_S186 13th_C18_S179 13th_C1_S147 13th_C20_S142 13th_C21_S135 13th_C23_S187 13th_C27_S151
#> "0222" "0222" "0221" "0221" "0222" "01222" "0231"
#> 13th_C29_S188 13th_C31_S137 13th_C34_S181 13th_C36_S196 13th_C38_S145 13th_C39_S153 13th_C3_S132
#> "0221" "0222" "0113" "0232" "0221" "0124" "0221"
#> 13th_C46_S183 13th_C49_S155 13th_C4_S191 13th_C51_S170 13th_C52_S198 13th_C53_S205 13th_C54_S212
#> "0221" "0233" "0221" "0222" "0222" "0221" "0221"
#> 13th_C55_S156 13th_C57_S171 13th_C5_S184 13th_C60_S213 13th_C63_S172 13th_C66_S214 13th_C68_S165
#> "0222" "0211" "0222" "0121" "0222" "01122" "0222"
#> 13th_C69_S173 13th_C6_S177 13th_C70_S201 13th_C71_S208 13th_C72_S215 13th_C75_S159 13th_C76_S216
#> "0222" "0221" "0222" "0222" "0232" "0211" "01122"
#> 13th_C77_S209 13th_C79_S174 13th_C80_S167 13th_C81_S160 13th_C86_S168 13th_C88_S218 13th_C89_S211
#> "0221" "0222" "0212" "0212" "0221" "0222" "0222"
#> 13th_C8_S140 13th_C92_S169 13th_C93_S162 13th_C94_S219 13th_C96_S204 1st-61_S27 1st-C11_S58
#> "0233" "0221" "0221" "0124" "0124" "0111" "0111"
#> 1st-C13_S19 1st-C15_S3 1st-C18_S51 1st-C19_S20 1st-C20_S12 1st-C21_S4 1st-C32_S14
#> "0212" "0222" "024" "01122" "024" "0121" "0113"
#> 1st-C34_S54 1st-C39_S23 1st-C42_S71 1st-C50_S33 1st-C51_S41 1st-C53_S74 1st-C56_S34
#> "01222" "0212" "0113" "01122" "024" "024" "01121"
#> 1st-C57_S42 1st-C58_S76 1st-C59_S77 1st-C62_S35 1st-C64_S79 1st-C68_S36 1st-C69_S44
#> "01122" "0111" "024" "024" "0111" "01121" "0124"
#> 1st-C71_S83 1st-C73_S45 1st-C74_S37 1st-C75_S29 1st-C77_S86 1st-C78_S85 1st-C79_S46
#> "0121" "01122" "024" "01122" "0113" "01122" "0212"
#> 1st-C80_S38 1st-C8_S10 1st-C90_S91 1st-C96_S94 2nd-C11_S20 2nd-C15_S25 2nd-C16_S33
#> "01121" "024" "0111" "0211" "01121" "0111" "01121"
#> 2nd-C17_S32 2nd-C19_S39 2nd-C1_S3 2nd-C21_S37 2nd-C25_S49 2nd-C26_S50 2nd-C27_S51
#> "0111" "0212" "0222" "0113" "01232" "01121" "0212"
#> 2nd-C28_S55 2nd-C29_S56 2nd-C2_S2 2nd-C31_S61 2nd-C32_S62 2nd-C36_S69 2nd-C37_S73
#> "024" "0121" "0232" "0121" "0111" "024" "0211"
#> 2nd-C38_S74 2nd-C39_S75 2nd-C3_S1 2nd-C47_S92 2nd-C49_S4 2nd-C4_S9 2nd-C51_S6
#> "0111" "01121" "024" "0121" "0211" "024" "0212"
#> 2nd-C52_S10 2nd-C54_S12 2nd-C57_S18 2nd-C58_S22 2nd-C5_S8 2nd-C62_S29 2nd-C67_S40
#> "0212" "01222" "0121" "024" "0212" "0111" "01122"
#> 2nd-C69_S42 2nd-C6_S7 2nd-C72_S48 2nd-C74_S53 2nd-C75_S52 2nd-C76_S60 2nd-C77_S59
#> "0222" "0121" "0111" "0121" "01121" "01232" "01122"
#> 2nd-C7_S15 2nd-C80_S65 2nd-C81_S64 2nd-C83_S71 2nd-C86_S77 2nd-C87_S76 2nd-C88_S84
#> "0212" "01121" "0124" "0121" "0113" "0211" "0111"
#> 2nd-C8_S14 2nd-C93_S88 2nd-C94_S96 2nd-C95_S95 3rd-C11_S58 3rd-C12_S68 3rd-C18_S80
#> "01122" "0111" "0222" "0113" "0111" "01122" "0121"
#> 3rd-C1_S39 3rd-C20_S22 3rd-C21_S11 3rd-C23_S94 3rd-C25_S15 3rd-C26_S28 3rd-C27_S49
#> "01232" "01231" "0121" "024" "0212" "0121" "01122"
#> 3rd-C32_S31 3rd-C33_S50 3rd-C35_S23 3rd-C36_S2 3rd-C3_S2 3rd-C40_S57 3rd-C42_S74
#> "024" "0111" "0113" "0111" "024" "0124" "01222"
#> 3rd-C44_S32 3rd-C46_S93 3rd-C47_S35 3rd-C49_S60 3rd-C4_S25 3rd-C51_S87 3rd-C52_S86
#> "024" "01232" "01122" "01122" "0111" "0232" "024"
#> 3rd-C53_S67 3rd-C56_S90 3rd-C57_S5 3rd-C58_S3 3rd-C59_S91 3rd-C60_S10 3rd-C61_S64
#> "0111" "0212" "01121" "0111" "0111" "0211" "024"
#> 3rd-C63_S54 3rd-C65_S20 3rd-C67_S69 3rd-C68_S13 3rd-C69_S78 3rd-C6_S44 3rd-C71_S80
#> "024" "0113" "0121" "0124" "024" "0113" "0111"
#> 3rd-C76_S22 3rd-C79_S67 3rd-C7_S40 3rd-C82_S11 3rd-C84_S75 3rd-C85_S79 3rd-C85_S83
#> "0121" "01121" "024" "0111" "0111" "01121" "024"
#> 3rd-C86_S85 3rd-C87_S88 3rd-C88_S24 3rd-C91_S91 3rd-C92_S86 3rd-C95_S81 3rd-C96_S79
#> "0124" "01232" "0111" "01121" "0111" "01121" "0212"
#> 3rd-C9_S5 4th-61_S28 4th-C12_S19 4th-C14_S26 4th-C18_S31 4th-C22_S45 4th-C23_S44
#> "0113" "0111" "0121" "0111" "01122" "024" "0121"
#> 4th-C24_S43 4th-C26_S50 4th-C27_S51 4th-C28_S55 4th-C29_S56 4th-C32_S62 4th-C33_S63
#> "0111" "0111" "0233" "0124" "0121" "0124" "0121"
#> 4th-C35_S68 4th-C36_S69 4th-C37_S73 4th-C3_S1 4th-C40_S79 4th-C43_S85 4th-C45_S87
#> "024" "0113" "024" "024" "01121" "01231" "0212"
#> 4th-C49_S4 4th-C4_S9 4th-C50_S5 4th-C51_S6 4th-C56_S17 4th-C57_S18 4th-C59_S23
#> "0124" "01122" "024" "0121" "01122" "024" "0121"
#> 4th-C5_S8 4th-C62_S29 4th-C63_S30 4th-C64_S34 4th-C66_S36 4th-C67_S40 4th-C68_S41
#> "0111" "01121" "0121" "01121" "01121" "0113" "0222"
#> 4th-C69_S42 4th-C70_S46 4th-C73_S54 4th-C75_S52 4th-C78_S58 4th-C79_S66 4th-C7_S15
#> "0121" "01231" "01122" "01122" "01222" "01122" "0111"
#> 4th-C80_S65 4th-C81_S64 4th-C82_S72 4th-C83_S71 4th-C85_S78 4th-C86_S77 4th-C87_S76
#> "01121" "01221" "01121" "01122" "0111" "01121" "0124"
#> 4th-C88_S84 4th-C89_S83 4th-C8_S14 4th-C92_S89 4th-C93_S88 4th-C94_S96 4th-C95_S95
#> "01121" "0111" "0124" "01121" "0212" "01122" "01221"
#> 4th-C96_S94 4th-C9_S13 5th-C10_S92 5th-C11_S91 5th-C12_S90 5th-C14_S97 5th-C16_S98
#> "01122" "024" "0231" "0231" "01231" "0211" "0233"
#> 5th-C18_S96 5th-C19_S104 5th-C21_S102 5th-C25_S108 5th-C30_S105 5th-C34_S108 5th-C35_S109
#> "0211" "01221" "0121" "0233" "01221" "01121" "0113"
#> 5th-C40_S112 5th-C41_S113 5th-C42_S114 5th-C43_S121 5th-C45_S123 5th-C47_S118 5th-C49_S89
#> "0231" "0222" "0231" "0233" "0231" "01222" "0111"
#> 5th-C50_S90 5th-C54_S89 5th-C56_S95 5th-C57_S96 5th-C58_S93 5th-C59_S94 5th-C5_S85
#> "01221" "01221" "0231" "01223" "0231" "01223" "0111"
#> 5th-C64_S99 5th-C66_S101 5th-C67_S105 5th-C68_S106 5th-C69_S107 5th-C6_S84 5th-C70_S103
#> "01223" "01223" "0232" "01223" "01223" "024" "024"
#> 5th-C73_S111 5th-C74_S110 5th-C77_S107 5th-C7_S93 5th-C80_S116 5th-C81_S115 5th-C83_S111
#> "0231" "01223" "01223" "0111" "0212" "0231" "0222"
#> 5th-C87_S119 5th-C88_S117 5th-C90_S115 5th-C92_S124 5th-C9_S92 6th-C12_S18 6th-C15_S22
#> "024" "0231" "0113" "01223" "01121" "0111" "0211"
#> 6th-C16_S29 6th-C19_S35 6th-C1_S3 6th-C20_S34 6th-C21_S33 6th-C22_S39 6th-C23_S38
#> "0124" "0212" "0211" "0113" "01122" "0113" "0111"
#> 6th-C24_S37 6th-C25_S43 6th-C28_S49 6th-C29_S50 6th-C2_S2 6th-C30_S51 6th-C34_S61
#> "0113" "0212" "0212" "0111" "0113" "0113" "0221"
#> 6th-C40_S73 6th-C42_S75 6th-C45_S81 6th-C51_S6 6th-C53_S10 6th-C54_S11 6th-C57_S17
#> "0113" "0113" "0221" "0113" "01231" "0111" "0211"
#> 6th-C58_S20 6th-C59_S21 6th-C5_S8 6th-C62_S25 6th-C63_S26 6th-C64_S30 6th-C65_S31
#> "0211" "0111" "0121" "0212" "0111" "0211" "0121"
#> 6th-C66_S32 6th-C67_S36 6th-C71_S41 6th-C73_S48 6th-C75_S46 6th-C77_S53 6th-C79_S60
#> "0113" "0212" "0111" "0113" "0113" "0111" "0111"
#> 6th-C80_S59 6th-C82_S66 6th-C83_S65 6th-C84_S64 6th-C85_S72 6th-C87_S70 6th-C89_S77
#> "0113" "0211" "024" "0211" "0111" "01122" "0212"
#> 6th-C90_S76 6th-C91_S84 6th-C93_S82 6th-C9_S12 7th-C10_S19 7th-C11_S18 7th-C12_S17
#> "0211" "0124" "0124" "0221" "0113" "01122" "0212"
#> 7th-C14_S24 7th-C15_S23 7th-C17_S29 7th-C19_S36 7th-C1_S3 7th-C20_S35 7th-C21_S34
#> "01121" "0124" "01231" "0211" "0211" "0212" "0211"
#> 7th-C24_S40 7th-C25_S43 7th-C28_S48 7th-C2_S2 7th-C31_S53 7th-C32_S54 7th-C34_S59
#> "01121" "0111" "0212" "0212" "0113" "0121" "0121"
#> 7th-C36_S61 7th-C3_S1 7th-C40_S70 7th-C44_S76 7th-C45_S77 7th-C47_S81 7th-C49_S4
#> "01122" "0212" "01222" "01231" "0111" "0222" "0222"
#> 7th-C4_S8 7th-C50_S5 7th-C52_S9 7th-C53_S10 7th-C56_S15 7th-C57_S16 7th-C58_S20
#> "0212" "0113" "0212" "0111" "01231" "0212" "01121"
#> 7th-C59_S21 7th-C60_S22 7th-C62_S27 7th-C64_S31 7th-C65_S32 7th-C66_S33 7th-C68_S38
#> "0111" "0212" "0111" "0111" "0211" "0113" "01231"
#> 7th-C69_S39 7th-C72_S42 7th-C73_S47 7th-C76_S52 7th-C77_S51 7th-C79_S58 7th-C80_S57
#> "0121" "0124" "0113" "0232" "0111" "01122" "0113"
#> 7th-C81_S56 7th-C82_S64 7th-C84_S62 7th-C85_S69 7th-C88_S75 7th-C89_S74 7th-C8_S13
#> "0233" "01122" "0111" "0221" "01231" "0113" "0111"
#> 7th-C90_S73 7th-C94_S83 7th-C96_S82 8th-C10_S100 8th-C11_S99 8th-C18_S110 8th-C20_S116
#> "0111" "0211" "0111" "0111" "0121" "0222" "01232"
#> 8th-C21_S115 8th-C23_S121 8th-C24_S120 8th-C26_S126 8th-C28_S131 8th-C2_S85 8th-C34_S141
#> "0222" "024" "0111" "0221" "024" "0111" "0121"
#> 8th-C37_S146 8th-C38_S147 8th-C44_S155 8th-C47_S160 8th-C55_S96 8th-C57_S98 8th-C58_S101
#> "0222" "0211" "0113" "0211" "01122" "01122" "01121"
#> 8th-C59_S102 8th-C61_S107 8th-C64_S112 8th-C65_S113 8th-C67_S117 8th-C69_S119 8th-C6_S88
#> "0121" "0124" "0121" "0111" "01122" "0222" "01232"
#> 8th-C70_S123 8th-C73_S130 8th-C74_S129 8th-C75_S128 8th-C79_S140 8th-C7_S95 8th-C84_S143
#> "0211" "01221" "01122" "0211" "024" "0121" "0211"
#> 8th-C85_S150 8th-C87_S148 8th-C90_S152 8th-C91_S158 8th-C92_S157 8th-C94_S162 8th-C95_S161
#> "01122" "0111" "024" "0222" "01232" "024" "0121"
#> 9th-C10_S18 9th-C11_S17 9th-C13_S24 9th-C14_S23 9th-C15_S22 9th-C16_S30 9th-C17_S29
#> "0113" "0113" "0211" "0211" "0121" "0124" "0121"
#> 9th-C19_S36 9th-C1_S3 9th-C20_S35 9th-C22_S41 9th-C25_S45 9th-C28_S50 9th-C29_S51
#> "0121" "0113" "0222" "0233" "0211" "01232" "0121"
#> 9th-C2_S2 9th-C30_S52 9th-C36_S59 9th-C38_S64 9th-C3_S1 9th-C40_S69 9th-C41_S70
#> "0232" "0121" "01222" "0113" "0113" "01231" "0111"
#> 9th-C46_S79 9th-C49_S4 9th-C51_S6 9th-C52_S10 9th-C57_S16 9th-C59_S20 9th-C5_S8
#> "0113" "024" "0211" "024" "01122" "0212" "0121"
#> 9th-C61_S25 9th-C62_S26 9th-C64_S31 9th-C65_S32 9th-C66_S33 9th-C67_S37 9th-C69_S39
#> "01221" "0121" "0121" "0124" "01232" "0121" "0212"
#> 9th-C6_S7 9th-C70_S42 9th-C74_S48 9th-C75_S47 9th-C77_S53 9th-C79_S57 9th-C80_S56
#> "0113" "0111" "0121" "024" "0121" "024" "01122"
#> 9th-C81_S55 9th-C83_S61 9th-C84_S60 9th-C85_S68 9th-C86_S67 9th-C87_S66 9th-C88_S73
#> "0113" "01121" "01223" "0222" "0113" "0221" "0211"
#> 9th-C89_S72 9th-C8_S14 9th-C91_S78 9th-C92_S77 9th-C93_S76 9th-C94_S83 9th-C96_S81
#> "0113" "0113" "0212" "024" "0113" "0212" "01222"
#> 9th-C9_S13
#> "01122"
get_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 388))
#> 10th_C10_S104 10th_C11_S96 10th_C13_S61 10th_C14_S53 10th_C16_S105 10th_C17_S97 10th_C19_S62
#> "0123" "0211" "0111" "0124" "0123" "0211" "0113"
#> 10th_C1_S59 10th_C20_S54 10th_C23_S98 10th_C24_S90 10th_C28_S91 10th_C30_S107 10th_C31_S48
#> "0124" "0124" "0123" "0123" "0222" "0121" "0121"
#> 10th_C32_S56 10th_C33_S64 10th_C34_S92 10th_C37_S49 10th_C41_S101 10th_C42_S109 10th_C43_S50
#> "0211" "0211" "024" "0211" "0123" "0231" "0221"
#> 10th_C45_S66 10th_C46_S94 10th_C4_S103 10th_C50_S73 10th_C51_S80 10th_C52_S110 10th_C53_S118
#> "0121" "01222" "01221" "024" "0221" "024" "0221"
#> 10th_C54_S124 10th_C56_S74 10th_C57_S81 10th_C58_S111 10th_C5_S95 10th_C61_S68 10th_C63_S82
#> "0123" "01222" "0222" "0222" "0221" "0211" "0231"
#> 10th_C64_S112 10th_C66_S126 10th_C68_S75 10th_C6_S88 10th_C73_S84 10th_C74_S76 10th_C76_S128
#> "0211" "0211" "0123" "0222" "01221" "0121" "0124"
#> 10th_C77_S120 10th_C78_S114 10th_C7_S60 10th_C80_S77 10th_C81_S70 10th_C84_S115 10th_C85_S86
#> "0232" "0222" "01221" "0233" "0113" "0113" "0124"
#> 10th_C86_S78 10th_C87_S71 10th_C88_S130 10th_C8_S52 10th_C90_S116 10th_C95_S123 10th_C96_S117
#> "0231" "0231" "01221" "0123" "0121" "024" "0121"
#> 11th-C10_S63 11th-C12_S47 11th-C16_S64 11th-C21_S4 11th-C22_S65 11th-C24_S49 11th-C26_S12
#> "0222" "024" "0123" "0212" "0211" "01221" "0233"
#> 11th-C27_S19 11th-C2_S8 11th-C30_S66 11th-C33_S20 11th-C36_S67 11th-C37_S6 11th-C39_S21
#> "0212" "0232" "0222" "0123" "0123" "0221" "0123"
#> 11th-C40_S52 11th-C41_S60 11th-C43_S7 11th-C44_S15 11th-C49_S23 11th-C4_S62 11th-C51_S39
#> "01222" "0113" "0233" "0113" "0113" "0233" "0113"
#> 11th-C53_S78 11th-C54_S86 11th-C55_S24 11th-C56_S32 11th-C57_S40 11th-C58_S71 11th-C5_S54
#> "0113" "0212" "0233" "0232" "024" "01221" "0121"
#> 11th-C61_S25 11th-C62_S33 11th-C64_S72 11th-C66_S88 11th-C67_S26 11th-C68_S34 11th-C77_S82
#> "0123" "0222" "0231" "0111" "0221" "01221" "0232"
#> 11th-C7_S16 11th-C93_S30 12th-C10_S155 12th-C11_S147 12th-C12_S139 12th-C14_S190 12th-C15_S183
#> "0113" "0222" "0211" "0121" "0124" "0113" "0211"
#> 12th-C1_S195 12th-C20_S191 12th-C21_S184 12th-C23_S149 12th-C24_S141 12th-C25_S185 12th-C26_S192
#> "0221" "0123" "0211" "0221" "0113" "0124" "0124"
#> 12th-C28_S142 12th-C29_S150 12th-C30_S157 12th-C33_S200 12th-C35_S151 12th-C36_S158 12th-C37_S187
#> "0121" "01122" "0124" "0124" "0211" "0232" "0222"
#> 12th-C38_S194 12th-C39_S201 12th-C3_S181 12th-C40_S144 12th-C42_S159 12th-C46_S145 12th-C47_S153
#> "0211" "0221" "0211" "0221" "0113" "01222" "0211"
#> 12th-C48_S160 12th-C4_S154 12th-C50_S210 12th-C51_S217 12th-C53_S168 12th-C55_S203 12th-C56_S211
#> "0124" "0221" "024" "0124" "0231" "0113" "0233"
#> 12th-C57_S218 12th-C58_S162 12th-C59_S169 12th-C60_S176 12th-C63_S219 12th-C64_S163 12th-C65_S170
#> "024" "01121" "0111" "0111" "0121" "0111" "0113"
#> 12th-C67_S205 12th-C69_S135 12th-C71_S171 12th-C74_S214 12th-C75_S206 12th-C76_S177 12th-C7_S196
#> "0212" "01222" "0221" "0111" "0221" "0111" "0113"
#> 12th-C80_S215 12th-C81_S207 12th-C84_S165 12th-C85_S137 12th-C8_S189 12th-C90_S166 12th-C93_S209
#> "0121" "0121" "0111" "0123" "0221" "0113" "0212"
#> 12th-C94_S180 12th-C95_S174 12th-C96_S167 13th_C12_S178 13th_C13_S149 13th_C15_S134 13th_C16_S193
#> "01222" "01121" "0111" "0124" "0121" "0212" "0124"
#> 13th_C17_S186 13th_C18_S179 13th_C1_S147 13th_C20_S142 13th_C21_S135 13th_C23_S187 13th_C27_S151
#> "0222" "0222" "0221" "0221" "0222" "01222" "0231"
#> 13th_C29_S188 13th_C31_S137 13th_C34_S181 13th_C36_S196 13th_C38_S145 13th_C39_S153 13th_C3_S132
#> "0221" "0222" "0113" "0232" "0221" "0124" "0221"
#> 13th_C46_S183 13th_C49_S155 13th_C4_S191 13th_C51_S170 13th_C52_S198 13th_C53_S205 13th_C54_S212
#> "0221" "0233" "0221" "0222" "0222" "0221" "0221"
#> 13th_C55_S156 13th_C57_S171 13th_C5_S184 13th_C60_S213 13th_C63_S172 13th_C66_S214 13th_C68_S165
#> "0222" "0211" "0222" "0121" "0222" "01122" "0222"
#> 13th_C69_S173 13th_C6_S177 13th_C70_S201 13th_C71_S208 13th_C72_S215 13th_C75_S159 13th_C76_S216
#> "0222" "0221" "0222" "0222" "0232" "0211" "01122"
#> 13th_C77_S209 13th_C79_S174 13th_C80_S167 13th_C81_S160 13th_C86_S168 13th_C88_S218 13th_C89_S211
#> "0221" "0222" "0212" "0212" "0221" "0222" "0222"
#> 13th_C8_S140 13th_C92_S169 13th_C93_S162 13th_C94_S219 13th_C96_S204 1st-61_S27 1st-C11_S58
#> "0233" "0221" "0221" "0124" "0124" "0111" "0111"
#> 1st-C13_S19 1st-C15_S3 1st-C18_S51 1st-C19_S20 1st-C20_S12 1st-C21_S4 1st-C32_S14
#> "0212" "0222" "024" "01122" "024" "0121" "0113"
#> 1st-C34_S54 1st-C39_S23 1st-C42_S71 1st-C50_S33 1st-C51_S41 1st-C53_S74 1st-C56_S34
#> "01222" "0212" "0113" "01122" "024" "024" "01121"
#> 1st-C57_S42 1st-C58_S76 1st-C59_S77 1st-C62_S35 1st-C64_S79 1st-C68_S36 1st-C69_S44
#> "01122" "0111" "024" "024" "0111" "01121" "0124"
#> 1st-C71_S83 1st-C73_S45 1st-C74_S37 1st-C75_S29 1st-C77_S86 1st-C78_S85 1st-C79_S46
#> "0121" "01122" "024" "01122" "0113" "01122" "0212"
#> 1st-C80_S38 1st-C8_S10 1st-C90_S91 1st-C96_S94 2nd-C11_S20 2nd-C15_S25 2nd-C16_S33
#> "01121" "024" "0111" "0211" "01121" "0111" "01121"
#> 2nd-C17_S32 2nd-C19_S39 2nd-C1_S3 2nd-C21_S37 2nd-C25_S49 2nd-C26_S50 2nd-C27_S51
#> "0111" "0212" "0222" "0113" "0123" "01121" "0212"
#> 2nd-C28_S55 2nd-C29_S56 2nd-C2_S2 2nd-C31_S61 2nd-C32_S62 2nd-C36_S69 2nd-C37_S73
#> "024" "0121" "0232" "0121" "0111" "024" "0211"
#> 2nd-C38_S74 2nd-C39_S75 2nd-C3_S1 2nd-C47_S92 2nd-C49_S4 2nd-C4_S9 2nd-C51_S6
#> "0111" "01121" "024" "0121" "0211" "024" "0212"
#> 2nd-C52_S10 2nd-C54_S12 2nd-C57_S18 2nd-C58_S22 2nd-C5_S8 2nd-C62_S29 2nd-C67_S40
#> "0212" "01222" "0121" "024" "0212" "0111" "01122"
#> 2nd-C69_S42 2nd-C6_S7 2nd-C72_S48 2nd-C74_S53 2nd-C75_S52 2nd-C76_S60 2nd-C77_S59
#> "0222" "0121" "0111" "0121" "01121" "0123" "01122"
#> 2nd-C7_S15 2nd-C80_S65 2nd-C81_S64 2nd-C83_S71 2nd-C86_S77 2nd-C87_S76 2nd-C88_S84
#> "0212" "01121" "0124" "0121" "0113" "0211" "0111"
#> 2nd-C8_S14 2nd-C93_S88 2nd-C94_S96 2nd-C95_S95 3rd-C11_S58 3rd-C12_S68 3rd-C18_S80
#> "01122" "0111" "0222" "0113" "0111" "01122" "0121"
#> 3rd-C1_S39 3rd-C20_S22 3rd-C21_S11 3rd-C23_S94 3rd-C25_S15 3rd-C26_S28 3rd-C27_S49
#> "0123" "0123" "0121" "024" "0212" "0121" "01122"
#> 3rd-C32_S31 3rd-C33_S50 3rd-C35_S23 3rd-C36_S2 3rd-C3_S2 3rd-C40_S57 3rd-C42_S74
#> "024" "0111" "0113" "0111" "024" "0124" "01222"
#> 3rd-C44_S32 3rd-C46_S93 3rd-C47_S35 3rd-C49_S60 3rd-C4_S25 3rd-C51_S87 3rd-C52_S86
#> "024" "0123" "01122" "01122" "0111" "0232" "024"
#> 3rd-C53_S67 3rd-C56_S90 3rd-C57_S5 3rd-C58_S3 3rd-C59_S91 3rd-C60_S10 3rd-C61_S64
#> "0111" "0212" "01121" "0111" "0111" "0211" "024"
#> 3rd-C63_S54 3rd-C65_S20 3rd-C67_S69 3rd-C68_S13 3rd-C69_S78 3rd-C6_S44 3rd-C71_S80
#> "024" "0113" "0121" "0124" "024" "0113" "0111"
#> 3rd-C76_S22 3rd-C79_S67 3rd-C7_S40 3rd-C82_S11 3rd-C84_S75 3rd-C85_S79 3rd-C85_S83
#> "0121" "01121" "024" "0111" "0111" "01121" "024"
#> 3rd-C86_S85 3rd-C87_S88 3rd-C88_S24 3rd-C91_S91 3rd-C92_S86 3rd-C95_S81 3rd-C96_S79
#> "0124" "0123" "0111" "01121" "0111" "01121" "0212"
#> 3rd-C9_S5 4th-61_S28 4th-C12_S19 4th-C14_S26 4th-C18_S31 4th-C22_S45 4th-C23_S44
#> "0113" "0111" "0121" "0111" "01122" "024" "0121"
#> 4th-C24_S43 4th-C26_S50 4th-C27_S51 4th-C28_S55 4th-C29_S56 4th-C32_S62 4th-C33_S63
#> "0111" "0111" "0233" "0124" "0121" "0124" "0121"
#> 4th-C35_S68 4th-C36_S69 4th-C37_S73 4th-C3_S1 4th-C40_S79 4th-C43_S85 4th-C45_S87
#> "024" "0113" "024" "024" "01121" "0123" "0212"
#> 4th-C49_S4 4th-C4_S9 4th-C50_S5 4th-C51_S6 4th-C56_S17 4th-C57_S18 4th-C59_S23
#> "0124" "01122" "024" "0121" "01122" "024" "0121"
#> 4th-C5_S8 4th-C62_S29 4th-C63_S30 4th-C64_S34 4th-C66_S36 4th-C67_S40 4th-C68_S41
#> "0111" "01121" "0121" "01121" "01121" "0113" "0222"
#> 4th-C69_S42 4th-C70_S46 4th-C73_S54 4th-C75_S52 4th-C78_S58 4th-C79_S66 4th-C7_S15
#> "0121" "0123" "01122" "01122" "01222" "01122" "0111"
#> 4th-C80_S65 4th-C81_S64 4th-C82_S72 4th-C83_S71 4th-C85_S78 4th-C86_S77 4th-C87_S76
#> "01121" "01221" "01121" "01122" "0111" "01121" "0124"
#> 4th-C88_S84 4th-C89_S83 4th-C8_S14 4th-C92_S89 4th-C93_S88 4th-C94_S96 4th-C95_S95
#> "01121" "0111" "0124" "01121" "0212" "01122" "01221"
#> 4th-C96_S94 4th-C9_S13 5th-C10_S92 5th-C11_S91 5th-C12_S90 5th-C14_S97 5th-C16_S98
#> "01122" "024" "0231" "0231" "0123" "0211" "0233"
#> 5th-C18_S96 5th-C19_S104 5th-C21_S102 5th-C25_S108 5th-C30_S105 5th-C34_S108 5th-C35_S109
#> "0211" "01221" "0121" "0233" "01221" "01121" "0113"
#> 5th-C40_S112 5th-C41_S113 5th-C42_S114 5th-C43_S121 5th-C45_S123 5th-C47_S118 5th-C49_S89
#> "0231" "0222" "0231" "0233" "0231" "01222" "0111"
#> 5th-C50_S90 5th-C54_S89 5th-C56_S95 5th-C57_S96 5th-C58_S93 5th-C59_S94 5th-C5_S85
#> "01221" "01221" "0231" "01223" "0231" "01223" "0111"
#> 5th-C64_S99 5th-C66_S101 5th-C67_S105 5th-C68_S106 5th-C69_S107 5th-C6_S84 5th-C70_S103
#> "01223" "01223" "0232" "01223" "01223" "024" "024"
#> 5th-C73_S111 5th-C74_S110 5th-C77_S107 5th-C7_S93 5th-C80_S116 5th-C81_S115 5th-C83_S111
#> "0231" "01223" "01223" "0111" "0212" "0231" "0222"
#> 5th-C87_S119 5th-C88_S117 5th-C90_S115 5th-C92_S124 5th-C9_S92 6th-C12_S18 6th-C15_S22
#> "024" "0231" "0113" "01223" "01121" "0111" "0211"
#> 6th-C16_S29 6th-C19_S35 6th-C1_S3 6th-C20_S34 6th-C21_S33 6th-C22_S39 6th-C23_S38
#> "0124" "0212" "0211" "0113" "01122" "0113" "0111"
#> 6th-C24_S37 6th-C25_S43 6th-C28_S49 6th-C29_S50 6th-C2_S2 6th-C30_S51 6th-C34_S61
#> "0113" "0212" "0212" "0111" "0113" "0113" "0221"
#> 6th-C40_S73 6th-C42_S75 6th-C45_S81 6th-C51_S6 6th-C53_S10 6th-C54_S11 6th-C57_S17
#> "0113" "0113" "0221" "0113" "0123" "0111" "0211"
#> 6th-C58_S20 6th-C59_S21 6th-C5_S8 6th-C62_S25 6th-C63_S26 6th-C64_S30 6th-C65_S31
#> "0211" "0111" "0121" "0212" "0111" "0211" "0121"
#> 6th-C66_S32 6th-C67_S36 6th-C71_S41 6th-C73_S48 6th-C75_S46 6th-C77_S53 6th-C79_S60
#> "0113" "0212" "0111" "0113" "0113" "0111" "0111"
#> 6th-C80_S59 6th-C82_S66 6th-C83_S65 6th-C84_S64 6th-C85_S72 6th-C87_S70 6th-C89_S77
#> "0113" "0211" "024" "0211" "0111" "01122" "0212"
#> 6th-C90_S76 6th-C91_S84 6th-C93_S82 6th-C9_S12 7th-C10_S19 7th-C11_S18 7th-C12_S17
#> "0211" "0124" "0124" "0221" "0113" "01122" "0212"
#> 7th-C14_S24 7th-C15_S23 7th-C17_S29 7th-C19_S36 7th-C1_S3 7th-C20_S35 7th-C21_S34
#> "01121" "0124" "0123" "0211" "0211" "0212" "0211"
#> 7th-C24_S40 7th-C25_S43 7th-C28_S48 7th-C2_S2 7th-C31_S53 7th-C32_S54 7th-C34_S59
#> "01121" "0111" "0212" "0212" "0113" "0121" "0121"
#> 7th-C36_S61 7th-C3_S1 7th-C40_S70 7th-C44_S76 7th-C45_S77 7th-C47_S81 7th-C49_S4
#> "01122" "0212" "01222" "0123" "0111" "0222" "0222"
#> 7th-C4_S8 7th-C50_S5 7th-C52_S9 7th-C53_S10 7th-C56_S15 7th-C57_S16 7th-C58_S20
#> "0212" "0113" "0212" "0111" "0123" "0212" "01121"
#> 7th-C59_S21 7th-C60_S22 7th-C62_S27 7th-C64_S31 7th-C65_S32 7th-C66_S33 7th-C68_S38
#> "0111" "0212" "0111" "0111" "0211" "0113" "0123"
#> 7th-C69_S39 7th-C72_S42 7th-C73_S47 7th-C76_S52 7th-C77_S51 7th-C79_S58 7th-C80_S57
#> "0121" "0124" "0113" "0232" "0111" "01122" "0113"
#> 7th-C81_S56 7th-C82_S64 7th-C84_S62 7th-C85_S69 7th-C88_S75 7th-C89_S74 7th-C8_S13
#> "0233" "01122" "0111" "0221" "0123" "0113" "0111"
#> 7th-C90_S73 7th-C94_S83 7th-C96_S82 8th-C10_S100 8th-C11_S99 8th-C18_S110 8th-C20_S116
#> "0111" "0211" "0111" "0111" "0121" "0222" "0123"
#> 8th-C21_S115 8th-C23_S121 8th-C24_S120 8th-C26_S126 8th-C28_S131 8th-C2_S85 8th-C34_S141
#> "0222" "024" "0111" "0221" "024" "0111" "0121"
#> 8th-C37_S146 8th-C38_S147 8th-C44_S155 8th-C47_S160 8th-C55_S96 8th-C57_S98 8th-C58_S101
#> "0222" "0211" "0113" "0211" "01122" "01122" "01121"
#> 8th-C59_S102 8th-C61_S107 8th-C64_S112 8th-C65_S113 8th-C67_S117 8th-C69_S119 8th-C6_S88
#> "0121" "0124" "0121" "0111" "01122" "0222" "0123"
#> 8th-C70_S123 8th-C73_S130 8th-C74_S129 8th-C75_S128 8th-C79_S140 8th-C7_S95 8th-C84_S143
#> "0211" "01221" "01122" "0211" "024" "0121" "0211"
#> 8th-C85_S150 8th-C87_S148 8th-C90_S152 8th-C91_S158 8th-C92_S157 8th-C94_S162 8th-C95_S161
#> "01122" "0111" "024" "0222" "0123" "024" "0121"
#> 9th-C10_S18 9th-C11_S17 9th-C13_S24 9th-C14_S23 9th-C15_S22 9th-C16_S30 9th-C17_S29
#> "0113" "0113" "0211" "0211" "0121" "0124" "0121"
#> 9th-C19_S36 9th-C1_S3 9th-C20_S35 9th-C22_S41 9th-C25_S45 9th-C28_S50 9th-C29_S51
#> "0121" "0113" "0222" "0233" "0211" "0123" "0121"
#> 9th-C2_S2 9th-C30_S52 9th-C36_S59 9th-C38_S64 9th-C3_S1 9th-C40_S69 9th-C41_S70
#> "0232" "0121" "01222" "0113" "0113" "0123" "0111"
#> 9th-C46_S79 9th-C49_S4 9th-C51_S6 9th-C52_S10 9th-C57_S16 9th-C59_S20 9th-C5_S8
#> "0113" "024" "0211" "024" "01122" "0212" "0121"
#> 9th-C61_S25 9th-C62_S26 9th-C64_S31 9th-C65_S32 9th-C66_S33 9th-C67_S37 9th-C69_S39
#> "01221" "0121" "0121" "0124" "0123" "0121" "0212"
#> 9th-C6_S7 9th-C70_S42 9th-C74_S48 9th-C75_S47 9th-C77_S53 9th-C79_S57 9th-C80_S56
#> "0113" "0111" "0121" "024" "0121" "024" "01122"
#> 9th-C81_S55 9th-C83_S61 9th-C84_S60 9th-C85_S68 9th-C86_S67 9th-C87_S66 9th-C88_S73
#> "0113" "01121" "01223" "0222" "0113" "0221" "0211"
#> 9th-C89_S72 9th-C8_S14 9th-C91_S78 9th-C92_S77 9th-C93_S76 9th-C94_S83 9th-C96_S81
#> "0113" "0113" "0212" "024" "0113" "0212" "01222"
#> 9th-C9_S13
#> "01122"
get_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 507))
#> 10th_C10_S104 10th_C11_S96 10th_C13_S61 10th_C14_S53 10th_C16_S105 10th_C17_S97 10th_C19_S62
#> "0123" "0211" "0111" "0124" "0123" "0211" "0113"
#> 10th_C1_S59 10th_C20_S54 10th_C23_S98 10th_C24_S90 10th_C28_S91 10th_C30_S107 10th_C31_S48
#> "0124" "0124" "0123" "0123" "0222" "0121" "0121"
#> 10th_C32_S56 10th_C33_S64 10th_C34_S92 10th_C37_S49 10th_C41_S101 10th_C42_S109 10th_C43_S50
#> "0211" "0211" "024" "0211" "0123" "0231" "0221"
#> 10th_C45_S66 10th_C46_S94 10th_C4_S103 10th_C50_S73 10th_C51_S80 10th_C52_S110 10th_C53_S118
#> "0121" "01222" "01221" "024" "0221" "024" "0221"
#> 10th_C54_S124 10th_C56_S74 10th_C57_S81 10th_C58_S111 10th_C5_S95 10th_C61_S68 10th_C63_S82
#> "0123" "01222" "0222" "0222" "0221" "0211" "0231"
#> 10th_C64_S112 10th_C66_S126 10th_C68_S75 10th_C6_S88 10th_C73_S84 10th_C74_S76 10th_C76_S128
#> "0211" "0211" "0123" "0222" "01221" "0121" "0124"
#> 10th_C77_S120 10th_C78_S114 10th_C7_S60 10th_C80_S77 10th_C81_S70 10th_C84_S115 10th_C85_S86
#> "0232" "0222" "01221" "0233" "0113" "0113" "0124"
#> 10th_C86_S78 10th_C87_S71 10th_C88_S130 10th_C8_S52 10th_C90_S116 10th_C95_S123 10th_C96_S117
#> "0231" "0231" "01221" "0123" "0121" "024" "0121"
#> 11th-C10_S63 11th-C12_S47 11th-C16_S64 11th-C21_S4 11th-C22_S65 11th-C24_S49 11th-C26_S12
#> "0222" "024" "0123" "0212" "0211" "01221" "0233"
#> 11th-C27_S19 11th-C2_S8 11th-C30_S66 11th-C33_S20 11th-C36_S67 11th-C37_S6 11th-C39_S21
#> "0212" "0232" "0222" "0123" "0123" "0221" "0123"
#> 11th-C40_S52 11th-C41_S60 11th-C43_S7 11th-C44_S15 11th-C49_S23 11th-C4_S62 11th-C51_S39
#> "01222" "0113" "0233" "0113" "0113" "0233" "0113"
#> 11th-C53_S78 11th-C54_S86 11th-C55_S24 11th-C56_S32 11th-C57_S40 11th-C58_S71 11th-C5_S54
#> "0113" "0212" "0233" "0232" "024" "01221" "0121"
#> 11th-C61_S25 11th-C62_S33 11th-C64_S72 11th-C66_S88 11th-C67_S26 11th-C68_S34 11th-C77_S82
#> "0123" "0222" "0231" "0111" "0221" "01221" "0232"
#> 11th-C7_S16 11th-C93_S30 12th-C10_S155 12th-C11_S147 12th-C12_S139 12th-C14_S190 12th-C15_S183
#> "0113" "0222" "0211" "0121" "0124" "0113" "0211"
#> 12th-C1_S195 12th-C20_S191 12th-C21_S184 12th-C23_S149 12th-C24_S141 12th-C25_S185 12th-C26_S192
#> "0221" "0123" "0211" "0221" "0113" "0124" "0124"
#> 12th-C28_S142 12th-C29_S150 12th-C30_S157 12th-C33_S200 12th-C35_S151 12th-C36_S158 12th-C37_S187
#> "0121" "0112" "0124" "0124" "0211" "0232" "0222"
#> 12th-C38_S194 12th-C39_S201 12th-C3_S181 12th-C40_S144 12th-C42_S159 12th-C46_S145 12th-C47_S153
#> "0211" "0221" "0211" "0221" "0113" "01222" "0211"
#> 12th-C48_S160 12th-C4_S154 12th-C50_S210 12th-C51_S217 12th-C53_S168 12th-C55_S203 12th-C56_S211
#> "0124" "0221" "024" "0124" "0231" "0113" "0233"
#> 12th-C57_S218 12th-C58_S162 12th-C59_S169 12th-C60_S176 12th-C63_S219 12th-C64_S163 12th-C65_S170
#> "024" "0112" "0111" "0111" "0121" "0111" "0113"
#> 12th-C67_S205 12th-C69_S135 12th-C71_S171 12th-C74_S214 12th-C75_S206 12th-C76_S177 12th-C7_S196
#> "0212" "01222" "0221" "0111" "0221" "0111" "0113"
#> 12th-C80_S215 12th-C81_S207 12th-C84_S165 12th-C85_S137 12th-C8_S189 12th-C90_S166 12th-C93_S209
#> "0121" "0121" "0111" "0123" "0221" "0113" "0212"
#> 12th-C94_S180 12th-C95_S174 12th-C96_S167 13th_C12_S178 13th_C13_S149 13th_C15_S134 13th_C16_S193
#> "01222" "0112" "0111" "0124" "0121" "0212" "0124"
#> 13th_C17_S186 13th_C18_S179 13th_C1_S147 13th_C20_S142 13th_C21_S135 13th_C23_S187 13th_C27_S151
#> "0222" "0222" "0221" "0221" "0222" "01222" "0231"
#> 13th_C29_S188 13th_C31_S137 13th_C34_S181 13th_C36_S196 13th_C38_S145 13th_C39_S153 13th_C3_S132
#> "0221" "0222" "0113" "0232" "0221" "0124" "0221"
#> 13th_C46_S183 13th_C49_S155 13th_C4_S191 13th_C51_S170 13th_C52_S198 13th_C53_S205 13th_C54_S212
#> "0221" "0233" "0221" "0222" "0222" "0221" "0221"
#> 13th_C55_S156 13th_C57_S171 13th_C5_S184 13th_C60_S213 13th_C63_S172 13th_C66_S214 13th_C68_S165
#> "0222" "0211" "0222" "0121" "0222" "0112" "0222"
#> 13th_C69_S173 13th_C6_S177 13th_C70_S201 13th_C71_S208 13th_C72_S215 13th_C75_S159 13th_C76_S216
#> "0222" "0221" "0222" "0222" "0232" "0211" "0112"
#> 13th_C77_S209 13th_C79_S174 13th_C80_S167 13th_C81_S160 13th_C86_S168 13th_C88_S218 13th_C89_S211
#> "0221" "0222" "0212" "0212" "0221" "0222" "0222"
#> 13th_C8_S140 13th_C92_S169 13th_C93_S162 13th_C94_S219 13th_C96_S204 1st-61_S27 1st-C11_S58
#> "0233" "0221" "0221" "0124" "0124" "0111" "0111"
#> 1st-C13_S19 1st-C15_S3 1st-C18_S51 1st-C19_S20 1st-C20_S12 1st-C21_S4 1st-C32_S14
#> "0212" "0222" "024" "0112" "024" "0121" "0113"
#> 1st-C34_S54 1st-C39_S23 1st-C42_S71 1st-C50_S33 1st-C51_S41 1st-C53_S74 1st-C56_S34
#> "01222" "0212" "0113" "0112" "024" "024" "0112"
#> 1st-C57_S42 1st-C58_S76 1st-C59_S77 1st-C62_S35 1st-C64_S79 1st-C68_S36 1st-C69_S44
#> "0112" "0111" "024" "024" "0111" "0112" "0124"
#> 1st-C71_S83 1st-C73_S45 1st-C74_S37 1st-C75_S29 1st-C77_S86 1st-C78_S85 1st-C79_S46
#> "0121" "0112" "024" "0112" "0113" "0112" "0212"
#> 1st-C80_S38 1st-C8_S10 1st-C90_S91 1st-C96_S94 2nd-C11_S20 2nd-C15_S25 2nd-C16_S33
#> "0112" "024" "0111" "0211" "0112" "0111" "0112"
#> 2nd-C17_S32 2nd-C19_S39 2nd-C1_S3 2nd-C21_S37 2nd-C25_S49 2nd-C26_S50 2nd-C27_S51
#> "0111" "0212" "0222" "0113" "0123" "0112" "0212"
#> 2nd-C28_S55 2nd-C29_S56 2nd-C2_S2 2nd-C31_S61 2nd-C32_S62 2nd-C36_S69 2nd-C37_S73
#> "024" "0121" "0232" "0121" "0111" "024" "0211"
#> 2nd-C38_S74 2nd-C39_S75 2nd-C3_S1 2nd-C47_S92 2nd-C49_S4 2nd-C4_S9 2nd-C51_S6
#> "0111" "0112" "024" "0121" "0211" "024" "0212"
#> 2nd-C52_S10 2nd-C54_S12 2nd-C57_S18 2nd-C58_S22 2nd-C5_S8 2nd-C62_S29 2nd-C67_S40
#> "0212" "01222" "0121" "024" "0212" "0111" "0112"
#> 2nd-C69_S42 2nd-C6_S7 2nd-C72_S48 2nd-C74_S53 2nd-C75_S52 2nd-C76_S60 2nd-C77_S59
#> "0222" "0121" "0111" "0121" "0112" "0123" "0112"
#> 2nd-C7_S15 2nd-C80_S65 2nd-C81_S64 2nd-C83_S71 2nd-C86_S77 2nd-C87_S76 2nd-C88_S84
#> "0212" "0112" "0124" "0121" "0113" "0211" "0111"
#> 2nd-C8_S14 2nd-C93_S88 2nd-C94_S96 2nd-C95_S95 3rd-C11_S58 3rd-C12_S68 3rd-C18_S80
#> "0112" "0111" "0222" "0113" "0111" "0112" "0121"
#> 3rd-C1_S39 3rd-C20_S22 3rd-C21_S11 3rd-C23_S94 3rd-C25_S15 3rd-C26_S28 3rd-C27_S49
#> "0123" "0123" "0121" "024" "0212" "0121" "0112"
#> 3rd-C32_S31 3rd-C33_S50 3rd-C35_S23 3rd-C36_S2 3rd-C3_S2 3rd-C40_S57 3rd-C42_S74
#> "024" "0111" "0113" "0111" "024" "0124" "01222"
#> 3rd-C44_S32 3rd-C46_S93 3rd-C47_S35 3rd-C49_S60 3rd-C4_S25 3rd-C51_S87 3rd-C52_S86
#> "024" "0123" "0112" "0112" "0111" "0232" "024"
#> 3rd-C53_S67 3rd-C56_S90 3rd-C57_S5 3rd-C58_S3 3rd-C59_S91 3rd-C60_S10 3rd-C61_S64
#> "0111" "0212" "0112" "0111" "0111" "0211" "024"
#> 3rd-C63_S54 3rd-C65_S20 3rd-C67_S69 3rd-C68_S13 3rd-C69_S78 3rd-C6_S44 3rd-C71_S80
#> "024" "0113" "0121" "0124" "024" "0113" "0111"
#> 3rd-C76_S22 3rd-C79_S67 3rd-C7_S40 3rd-C82_S11 3rd-C84_S75 3rd-C85_S79 3rd-C85_S83
#> "0121" "0112" "024" "0111" "0111" "0112" "024"
#> 3rd-C86_S85 3rd-C87_S88 3rd-C88_S24 3rd-C91_S91 3rd-C92_S86 3rd-C95_S81 3rd-C96_S79
#> "0124" "0123" "0111" "0112" "0111" "0112" "0212"
#> 3rd-C9_S5 4th-61_S28 4th-C12_S19 4th-C14_S26 4th-C18_S31 4th-C22_S45 4th-C23_S44
#> "0113" "0111" "0121" "0111" "0112" "024" "0121"
#> 4th-C24_S43 4th-C26_S50 4th-C27_S51 4th-C28_S55 4th-C29_S56 4th-C32_S62 4th-C33_S63
#> "0111" "0111" "0233" "0124" "0121" "0124" "0121"
#> 4th-C35_S68 4th-C36_S69 4th-C37_S73 4th-C3_S1 4th-C40_S79 4th-C43_S85 4th-C45_S87
#> "024" "0113" "024" "024" "0112" "0123" "0212"
#> 4th-C49_S4 4th-C4_S9 4th-C50_S5 4th-C51_S6 4th-C56_S17 4th-C57_S18 4th-C59_S23
#> "0124" "0112" "024" "0121" "0112" "024" "0121"
#> 4th-C5_S8 4th-C62_S29 4th-C63_S30 4th-C64_S34 4th-C66_S36 4th-C67_S40 4th-C68_S41
#> "0111" "0112" "0121" "0112" "0112" "0113" "0222"
#> 4th-C69_S42 4th-C70_S46 4th-C73_S54 4th-C75_S52 4th-C78_S58 4th-C79_S66 4th-C7_S15
#> "0121" "0123" "0112" "0112" "01222" "0112" "0111"
#> 4th-C80_S65 4th-C81_S64 4th-C82_S72 4th-C83_S71 4th-C85_S78 4th-C86_S77 4th-C87_S76
#> "0112" "01221" "0112" "0112" "0111" "0112" "0124"
#> 4th-C88_S84 4th-C89_S83 4th-C8_S14 4th-C92_S89 4th-C93_S88 4th-C94_S96 4th-C95_S95
#> "0112" "0111" "0124" "0112" "0212" "0112" "01221"
#> 4th-C96_S94 4th-C9_S13 5th-C10_S92 5th-C11_S91 5th-C12_S90 5th-C14_S97 5th-C16_S98
#> "0112" "024" "0231" "0231" "0123" "0211" "0233"
#> 5th-C18_S96 5th-C19_S104 5th-C21_S102 5th-C25_S108 5th-C30_S105 5th-C34_S108 5th-C35_S109
#> "0211" "01221" "0121" "0233" "01221" "0112" "0113"
#> 5th-C40_S112 5th-C41_S113 5th-C42_S114 5th-C43_S121 5th-C45_S123 5th-C47_S118 5th-C49_S89
#> "0231" "0222" "0231" "0233" "0231" "01222" "0111"
#> 5th-C50_S90 5th-C54_S89 5th-C56_S95 5th-C57_S96 5th-C58_S93 5th-C59_S94 5th-C5_S85
#> "01221" "01221" "0231" "01223" "0231" "01223" "0111"
#> 5th-C64_S99 5th-C66_S101 5th-C67_S105 5th-C68_S106 5th-C69_S107 5th-C6_S84 5th-C70_S103
#> "01223" "01223" "0232" "01223" "01223" "024" "024"
#> 5th-C73_S111 5th-C74_S110 5th-C77_S107 5th-C7_S93 5th-C80_S116 5th-C81_S115 5th-C83_S111
#> "0231" "01223" "01223" "0111" "0212" "0231" "0222"
#> 5th-C87_S119 5th-C88_S117 5th-C90_S115 5th-C92_S124 5th-C9_S92 6th-C12_S18 6th-C15_S22
#> "024" "0231" "0113" "01223" "0112" "0111" "0211"
#> 6th-C16_S29 6th-C19_S35 6th-C1_S3 6th-C20_S34 6th-C21_S33 6th-C22_S39 6th-C23_S38
#> "0124" "0212" "0211" "0113" "0112" "0113" "0111"
#> 6th-C24_S37 6th-C25_S43 6th-C28_S49 6th-C29_S50 6th-C2_S2 6th-C30_S51 6th-C34_S61
#> "0113" "0212" "0212" "0111" "0113" "0113" "0221"
#> 6th-C40_S73 6th-C42_S75 6th-C45_S81 6th-C51_S6 6th-C53_S10 6th-C54_S11 6th-C57_S17
#> "0113" "0113" "0221" "0113" "0123" "0111" "0211"
#> 6th-C58_S20 6th-C59_S21 6th-C5_S8 6th-C62_S25 6th-C63_S26 6th-C64_S30 6th-C65_S31
#> "0211" "0111" "0121" "0212" "0111" "0211" "0121"
#> 6th-C66_S32 6th-C67_S36 6th-C71_S41 6th-C73_S48 6th-C75_S46 6th-C77_S53 6th-C79_S60
#> "0113" "0212" "0111" "0113" "0113" "0111" "0111"
#> 6th-C80_S59 6th-C82_S66 6th-C83_S65 6th-C84_S64 6th-C85_S72 6th-C87_S70 6th-C89_S77
#> "0113" "0211" "024" "0211" "0111" "0112" "0212"
#> 6th-C90_S76 6th-C91_S84 6th-C93_S82 6th-C9_S12 7th-C10_S19 7th-C11_S18 7th-C12_S17
#> "0211" "0124" "0124" "0221" "0113" "0112" "0212"
#> 7th-C14_S24 7th-C15_S23 7th-C17_S29 7th-C19_S36 7th-C1_S3 7th-C20_S35 7th-C21_S34
#> "0112" "0124" "0123" "0211" "0211" "0212" "0211"
#> 7th-C24_S40 7th-C25_S43 7th-C28_S48 7th-C2_S2 7th-C31_S53 7th-C32_S54 7th-C34_S59
#> "0112" "0111" "0212" "0212" "0113" "0121" "0121"
#> 7th-C36_S61 7th-C3_S1 7th-C40_S70 7th-C44_S76 7th-C45_S77 7th-C47_S81 7th-C49_S4
#> "0112" "0212" "01222" "0123" "0111" "0222" "0222"
#> 7th-C4_S8 7th-C50_S5 7th-C52_S9 7th-C53_S10 7th-C56_S15 7th-C57_S16 7th-C58_S20
#> "0212" "0113" "0212" "0111" "0123" "0212" "0112"
#> 7th-C59_S21 7th-C60_S22 7th-C62_S27 7th-C64_S31 7th-C65_S32 7th-C66_S33 7th-C68_S38
#> "0111" "0212" "0111" "0111" "0211" "0113" "0123"
#> 7th-C69_S39 7th-C72_S42 7th-C73_S47 7th-C76_S52 7th-C77_S51 7th-C79_S58 7th-C80_S57
#> "0121" "0124" "0113" "0232" "0111" "0112" "0113"
#> 7th-C81_S56 7th-C82_S64 7th-C84_S62 7th-C85_S69 7th-C88_S75 7th-C89_S74 7th-C8_S13
#> "0233" "0112" "0111" "0221" "0123" "0113" "0111"
#> 7th-C90_S73 7th-C94_S83 7th-C96_S82 8th-C10_S100 8th-C11_S99 8th-C18_S110 8th-C20_S116
#> "0111" "0211" "0111" "0111" "0121" "0222" "0123"
#> 8th-C21_S115 8th-C23_S121 8th-C24_S120 8th-C26_S126 8th-C28_S131 8th-C2_S85 8th-C34_S141
#> "0222" "024" "0111" "0221" "024" "0111" "0121"
#> 8th-C37_S146 8th-C38_S147 8th-C44_S155 8th-C47_S160 8th-C55_S96 8th-C57_S98 8th-C58_S101
#> "0222" "0211" "0113" "0211" "0112" "0112" "0112"
#> 8th-C59_S102 8th-C61_S107 8th-C64_S112 8th-C65_S113 8th-C67_S117 8th-C69_S119 8th-C6_S88
#> "0121" "0124" "0121" "0111" "0112" "0222" "0123"
#> 8th-C70_S123 8th-C73_S130 8th-C74_S129 8th-C75_S128 8th-C79_S140 8th-C7_S95 8th-C84_S143
#> "0211" "01221" "0112" "0211" "024" "0121" "0211"
#> 8th-C85_S150 8th-C87_S148 8th-C90_S152 8th-C91_S158 8th-C92_S157 8th-C94_S162 8th-C95_S161
#> "0112" "0111" "024" "0222" "0123" "024" "0121"
#> 9th-C10_S18 9th-C11_S17 9th-C13_S24 9th-C14_S23 9th-C15_S22 9th-C16_S30 9th-C17_S29
#> "0113" "0113" "0211" "0211" "0121" "0124" "0121"
#> 9th-C19_S36 9th-C1_S3 9th-C20_S35 9th-C22_S41 9th-C25_S45 9th-C28_S50 9th-C29_S51
#> "0121" "0113" "0222" "0233" "0211" "0123" "0121"
#> 9th-C2_S2 9th-C30_S52 9th-C36_S59 9th-C38_S64 9th-C3_S1 9th-C40_S69 9th-C41_S70
#> "0232" "0121" "01222" "0113" "0113" "0123" "0111"
#> 9th-C46_S79 9th-C49_S4 9th-C51_S6 9th-C52_S10 9th-C57_S16 9th-C59_S20 9th-C5_S8
#> "0113" "024" "0211" "024" "0112" "0212" "0121"
#> 9th-C61_S25 9th-C62_S26 9th-C64_S31 9th-C65_S32 9th-C66_S33 9th-C67_S37 9th-C69_S39
#> "01221" "0121" "0121" "0124" "0123" "0121" "0212"
#> 9th-C6_S7 9th-C70_S42 9th-C74_S48 9th-C75_S47 9th-C77_S53 9th-C79_S57 9th-C80_S56
#> "0113" "0111" "0121" "024" "0121" "024" "0112"
#> 9th-C81_S55 9th-C83_S61 9th-C84_S60 9th-C85_S68 9th-C86_S67 9th-C87_S66 9th-C88_S73
#> "0113" "0112" "01223" "0222" "0113" "0221" "0211"
#> 9th-C89_S72 9th-C8_S14 9th-C91_S78 9th-C92_S77 9th-C93_S76 9th-C94_S83 9th-C96_S81
#> "0113" "0113" "0212" "024" "0113" "0212" "01222"
#> 9th-C9_S13
#> "0112"
get_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 545))
#> 10th_C10_S104 10th_C11_S96 10th_C13_S61 10th_C14_S53 10th_C16_S105 10th_C17_S97 10th_C19_S62
#> "0123" "0211" "0111" "0124" "0123" "0211" "0113"
#> 10th_C1_S59 10th_C20_S54 10th_C23_S98 10th_C24_S90 10th_C28_S91 10th_C30_S107 10th_C31_S48
#> "0124" "0124" "0123" "0123" "0222" "0121" "0121"
#> 10th_C32_S56 10th_C33_S64 10th_C34_S92 10th_C37_S49 10th_C41_S101 10th_C42_S109 10th_C43_S50
#> "0211" "0211" "024" "0211" "0123" "023" "0221"
#> 10th_C45_S66 10th_C46_S94 10th_C4_S103 10th_C50_S73 10th_C51_S80 10th_C52_S110 10th_C53_S118
#> "0121" "01222" "01221" "024" "0221" "024" "0221"
#> 10th_C54_S124 10th_C56_S74 10th_C57_S81 10th_C58_S111 10th_C5_S95 10th_C61_S68 10th_C63_S82
#> "0123" "01222" "0222" "0222" "0221" "0211" "023"
#> 10th_C64_S112 10th_C66_S126 10th_C68_S75 10th_C6_S88 10th_C73_S84 10th_C74_S76 10th_C76_S128
#> "0211" "0211" "0123" "0222" "01221" "0121" "0124"
#> 10th_C77_S120 10th_C78_S114 10th_C7_S60 10th_C80_S77 10th_C81_S70 10th_C84_S115 10th_C85_S86
#> "023" "0222" "01221" "023" "0113" "0113" "0124"
#> 10th_C86_S78 10th_C87_S71 10th_C88_S130 10th_C8_S52 10th_C90_S116 10th_C95_S123 10th_C96_S117
#> "023" "023" "01221" "0123" "0121" "024" "0121"
#> 11th-C10_S63 11th-C12_S47 11th-C16_S64 11th-C21_S4 11th-C22_S65 11th-C24_S49 11th-C26_S12
#> "0222" "024" "0123" "0212" "0211" "01221" "023"
#> 11th-C27_S19 11th-C2_S8 11th-C30_S66 11th-C33_S20 11th-C36_S67 11th-C37_S6 11th-C39_S21
#> "0212" "023" "0222" "0123" "0123" "0221" "0123"
#> 11th-C40_S52 11th-C41_S60 11th-C43_S7 11th-C44_S15 11th-C49_S23 11th-C4_S62 11th-C51_S39
#> "01222" "0113" "023" "0113" "0113" "023" "0113"
#> 11th-C53_S78 11th-C54_S86 11th-C55_S24 11th-C56_S32 11th-C57_S40 11th-C58_S71 11th-C5_S54
#> "0113" "0212" "023" "023" "024" "01221" "0121"
#> 11th-C61_S25 11th-C62_S33 11th-C64_S72 11th-C66_S88 11th-C67_S26 11th-C68_S34 11th-C77_S82
#> "0123" "0222" "023" "0111" "0221" "01221" "023"
#> 11th-C7_S16 11th-C93_S30 12th-C10_S155 12th-C11_S147 12th-C12_S139 12th-C14_S190 12th-C15_S183
#> "0113" "0222" "0211" "0121" "0124" "0113" "0211"
#> 12th-C1_S195 12th-C20_S191 12th-C21_S184 12th-C23_S149 12th-C24_S141 12th-C25_S185 12th-C26_S192
#> "0221" "0123" "0211" "0221" "0113" "0124" "0124"
#> 12th-C28_S142 12th-C29_S150 12th-C30_S157 12th-C33_S200 12th-C35_S151 12th-C36_S158 12th-C37_S187
#> "0121" "0112" "0124" "0124" "0211" "023" "0222"
#> 12th-C38_S194 12th-C39_S201 12th-C3_S181 12th-C40_S144 12th-C42_S159 12th-C46_S145 12th-C47_S153
#> "0211" "0221" "0211" "0221" "0113" "01222" "0211"
#> 12th-C48_S160 12th-C4_S154 12th-C50_S210 12th-C51_S217 12th-C53_S168 12th-C55_S203 12th-C56_S211
#> "0124" "0221" "024" "0124" "023" "0113" "023"
#> 12th-C57_S218 12th-C58_S162 12th-C59_S169 12th-C60_S176 12th-C63_S219 12th-C64_S163 12th-C65_S170
#> "024" "0112" "0111" "0111" "0121" "0111" "0113"
#> 12th-C67_S205 12th-C69_S135 12th-C71_S171 12th-C74_S214 12th-C75_S206 12th-C76_S177 12th-C7_S196
#> "0212" "01222" "0221" "0111" "0221" "0111" "0113"
#> 12th-C80_S215 12th-C81_S207 12th-C84_S165 12th-C85_S137 12th-C8_S189 12th-C90_S166 12th-C93_S209
#> "0121" "0121" "0111" "0123" "0221" "0113" "0212"
#> 12th-C94_S180 12th-C95_S174 12th-C96_S167 13th_C12_S178 13th_C13_S149 13th_C15_S134 13th_C16_S193
#> "01222" "0112" "0111" "0124" "0121" "0212" "0124"
#> 13th_C17_S186 13th_C18_S179 13th_C1_S147 13th_C20_S142 13th_C21_S135 13th_C23_S187 13th_C27_S151
#> "0222" "0222" "0221" "0221" "0222" "01222" "023"
#> 13th_C29_S188 13th_C31_S137 13th_C34_S181 13th_C36_S196 13th_C38_S145 13th_C39_S153 13th_C3_S132
#> "0221" "0222" "0113" "023" "0221" "0124" "0221"
#> 13th_C46_S183 13th_C49_S155 13th_C4_S191 13th_C51_S170 13th_C52_S198 13th_C53_S205 13th_C54_S212
#> "0221" "023" "0221" "0222" "0222" "0221" "0221"
#> 13th_C55_S156 13th_C57_S171 13th_C5_S184 13th_C60_S213 13th_C63_S172 13th_C66_S214 13th_C68_S165
#> "0222" "0211" "0222" "0121" "0222" "0112" "0222"
#> 13th_C69_S173 13th_C6_S177 13th_C70_S201 13th_C71_S208 13th_C72_S215 13th_C75_S159 13th_C76_S216
#> "0222" "0221" "0222" "0222" "023" "0211" "0112"
#> 13th_C77_S209 13th_C79_S174 13th_C80_S167 13th_C81_S160 13th_C86_S168 13th_C88_S218 13th_C89_S211
#> "0221" "0222" "0212" "0212" "0221" "0222" "0222"
#> 13th_C8_S140 13th_C92_S169 13th_C93_S162 13th_C94_S219 13th_C96_S204 1st-61_S27 1st-C11_S58
#> "023" "0221" "0221" "0124" "0124" "0111" "0111"
#> 1st-C13_S19 1st-C15_S3 1st-C18_S51 1st-C19_S20 1st-C20_S12 1st-C21_S4 1st-C32_S14
#> "0212" "0222" "024" "0112" "024" "0121" "0113"
#> 1st-C34_S54 1st-C39_S23 1st-C42_S71 1st-C50_S33 1st-C51_S41 1st-C53_S74 1st-C56_S34
#> "01222" "0212" "0113" "0112" "024" "024" "0112"
#> 1st-C57_S42 1st-C58_S76 1st-C59_S77 1st-C62_S35 1st-C64_S79 1st-C68_S36 1st-C69_S44
#> "0112" "0111" "024" "024" "0111" "0112" "0124"
#> 1st-C71_S83 1st-C73_S45 1st-C74_S37 1st-C75_S29 1st-C77_S86 1st-C78_S85 1st-C79_S46
#> "0121" "0112" "024" "0112" "0113" "0112" "0212"
#> 1st-C80_S38 1st-C8_S10 1st-C90_S91 1st-C96_S94 2nd-C11_S20 2nd-C15_S25 2nd-C16_S33
#> "0112" "024" "0111" "0211" "0112" "0111" "0112"
#> 2nd-C17_S32 2nd-C19_S39 2nd-C1_S3 2nd-C21_S37 2nd-C25_S49 2nd-C26_S50 2nd-C27_S51
#> "0111" "0212" "0222" "0113" "0123" "0112" "0212"
#> 2nd-C28_S55 2nd-C29_S56 2nd-C2_S2 2nd-C31_S61 2nd-C32_S62 2nd-C36_S69 2nd-C37_S73
#> "024" "0121" "023" "0121" "0111" "024" "0211"
#> 2nd-C38_S74 2nd-C39_S75 2nd-C3_S1 2nd-C47_S92 2nd-C49_S4 2nd-C4_S9 2nd-C51_S6
#> "0111" "0112" "024" "0121" "0211" "024" "0212"
#> 2nd-C52_S10 2nd-C54_S12 2nd-C57_S18 2nd-C58_S22 2nd-C5_S8 2nd-C62_S29 2nd-C67_S40
#> "0212" "01222" "0121" "024" "0212" "0111" "0112"
#> 2nd-C69_S42 2nd-C6_S7 2nd-C72_S48 2nd-C74_S53 2nd-C75_S52 2nd-C76_S60 2nd-C77_S59
#> "0222" "0121" "0111" "0121" "0112" "0123" "0112"
#> 2nd-C7_S15 2nd-C80_S65 2nd-C81_S64 2nd-C83_S71 2nd-C86_S77 2nd-C87_S76 2nd-C88_S84
#> "0212" "0112" "0124" "0121" "0113" "0211" "0111"
#> 2nd-C8_S14 2nd-C93_S88 2nd-C94_S96 2nd-C95_S95 3rd-C11_S58 3rd-C12_S68 3rd-C18_S80
#> "0112" "0111" "0222" "0113" "0111" "0112" "0121"
#> 3rd-C1_S39 3rd-C20_S22 3rd-C21_S11 3rd-C23_S94 3rd-C25_S15 3rd-C26_S28 3rd-C27_S49
#> "0123" "0123" "0121" "024" "0212" "0121" "0112"
#> 3rd-C32_S31 3rd-C33_S50 3rd-C35_S23 3rd-C36_S2 3rd-C3_S2 3rd-C40_S57 3rd-C42_S74
#> "024" "0111" "0113" "0111" "024" "0124" "01222"
#> 3rd-C44_S32 3rd-C46_S93 3rd-C47_S35 3rd-C49_S60 3rd-C4_S25 3rd-C51_S87 3rd-C52_S86
#> "024" "0123" "0112" "0112" "0111" "023" "024"
#> 3rd-C53_S67 3rd-C56_S90 3rd-C57_S5 3rd-C58_S3 3rd-C59_S91 3rd-C60_S10 3rd-C61_S64
#> "0111" "0212" "0112" "0111" "0111" "0211" "024"
#> 3rd-C63_S54 3rd-C65_S20 3rd-C67_S69 3rd-C68_S13 3rd-C69_S78 3rd-C6_S44 3rd-C71_S80
#> "024" "0113" "0121" "0124" "024" "0113" "0111"
#> 3rd-C76_S22 3rd-C79_S67 3rd-C7_S40 3rd-C82_S11 3rd-C84_S75 3rd-C85_S79 3rd-C85_S83
#> "0121" "0112" "024" "0111" "0111" "0112" "024"
#> 3rd-C86_S85 3rd-C87_S88 3rd-C88_S24 3rd-C91_S91 3rd-C92_S86 3rd-C95_S81 3rd-C96_S79
#> "0124" "0123" "0111" "0112" "0111" "0112" "0212"
#> 3rd-C9_S5 4th-61_S28 4th-C12_S19 4th-C14_S26 4th-C18_S31 4th-C22_S45 4th-C23_S44
#> "0113" "0111" "0121" "0111" "0112" "024" "0121"
#> 4th-C24_S43 4th-C26_S50 4th-C27_S51 4th-C28_S55 4th-C29_S56 4th-C32_S62 4th-C33_S63
#> "0111" "0111" "023" "0124" "0121" "0124" "0121"
#> 4th-C35_S68 4th-C36_S69 4th-C37_S73 4th-C3_S1 4th-C40_S79 4th-C43_S85 4th-C45_S87
#> "024" "0113" "024" "024" "0112" "0123" "0212"
#> 4th-C49_S4 4th-C4_S9 4th-C50_S5 4th-C51_S6 4th-C56_S17 4th-C57_S18 4th-C59_S23
#> "0124" "0112" "024" "0121" "0112" "024" "0121"
#> 4th-C5_S8 4th-C62_S29 4th-C63_S30 4th-C64_S34 4th-C66_S36 4th-C67_S40 4th-C68_S41
#> "0111" "0112" "0121" "0112" "0112" "0113" "0222"
#> 4th-C69_S42 4th-C70_S46 4th-C73_S54 4th-C75_S52 4th-C78_S58 4th-C79_S66 4th-C7_S15
#> "0121" "0123" "0112" "0112" "01222" "0112" "0111"
#> 4th-C80_S65 4th-C81_S64 4th-C82_S72 4th-C83_S71 4th-C85_S78 4th-C86_S77 4th-C87_S76
#> "0112" "01221" "0112" "0112" "0111" "0112" "0124"
#> 4th-C88_S84 4th-C89_S83 4th-C8_S14 4th-C92_S89 4th-C93_S88 4th-C94_S96 4th-C95_S95
#> "0112" "0111" "0124" "0112" "0212" "0112" "01221"
#> 4th-C96_S94 4th-C9_S13 5th-C10_S92 5th-C11_S91 5th-C12_S90 5th-C14_S97 5th-C16_S98
#> "0112" "024" "023" "023" "0123" "0211" "023"
#> 5th-C18_S96 5th-C19_S104 5th-C21_S102 5th-C25_S108 5th-C30_S105 5th-C34_S108 5th-C35_S109
#> "0211" "01221" "0121" "023" "01221" "0112" "0113"
#> 5th-C40_S112 5th-C41_S113 5th-C42_S114 5th-C43_S121 5th-C45_S123 5th-C47_S118 5th-C49_S89
#> "023" "0222" "023" "023" "023" "01222" "0111"
#> 5th-C50_S90 5th-C54_S89 5th-C56_S95 5th-C57_S96 5th-C58_S93 5th-C59_S94 5th-C5_S85
#> "01221" "01221" "023" "01223" "023" "01223" "0111"
#> 5th-C64_S99 5th-C66_S101 5th-C67_S105 5th-C68_S106 5th-C69_S107 5th-C6_S84 5th-C70_S103
#> "01223" "01223" "023" "01223" "01223" "024" "024"
#> 5th-C73_S111 5th-C74_S110 5th-C77_S107 5th-C7_S93 5th-C80_S116 5th-C81_S115 5th-C83_S111
#> "023" "01223" "01223" "0111" "0212" "023" "0222"
#> 5th-C87_S119 5th-C88_S117 5th-C90_S115 5th-C92_S124 5th-C9_S92 6th-C12_S18 6th-C15_S22
#> "024" "023" "0113" "01223" "0112" "0111" "0211"
#> 6th-C16_S29 6th-C19_S35 6th-C1_S3 6th-C20_S34 6th-C21_S33 6th-C22_S39 6th-C23_S38
#> "0124" "0212" "0211" "0113" "0112" "0113" "0111"
#> 6th-C24_S37 6th-C25_S43 6th-C28_S49 6th-C29_S50 6th-C2_S2 6th-C30_S51 6th-C34_S61
#> "0113" "0212" "0212" "0111" "0113" "0113" "0221"
#> 6th-C40_S73 6th-C42_S75 6th-C45_S81 6th-C51_S6 6th-C53_S10 6th-C54_S11 6th-C57_S17
#> "0113" "0113" "0221" "0113" "0123" "0111" "0211"
#> 6th-C58_S20 6th-C59_S21 6th-C5_S8 6th-C62_S25 6th-C63_S26 6th-C64_S30 6th-C65_S31
#> "0211" "0111" "0121" "0212" "0111" "0211" "0121"
#> 6th-C66_S32 6th-C67_S36 6th-C71_S41 6th-C73_S48 6th-C75_S46 6th-C77_S53 6th-C79_S60
#> "0113" "0212" "0111" "0113" "0113" "0111" "0111"
#> 6th-C80_S59 6th-C82_S66 6th-C83_S65 6th-C84_S64 6th-C85_S72 6th-C87_S70 6th-C89_S77
#> "0113" "0211" "024" "0211" "0111" "0112" "0212"
#> 6th-C90_S76 6th-C91_S84 6th-C93_S82 6th-C9_S12 7th-C10_S19 7th-C11_S18 7th-C12_S17
#> "0211" "0124" "0124" "0221" "0113" "0112" "0212"
#> 7th-C14_S24 7th-C15_S23 7th-C17_S29 7th-C19_S36 7th-C1_S3 7th-C20_S35 7th-C21_S34
#> "0112" "0124" "0123" "0211" "0211" "0212" "0211"
#> 7th-C24_S40 7th-C25_S43 7th-C28_S48 7th-C2_S2 7th-C31_S53 7th-C32_S54 7th-C34_S59
#> "0112" "0111" "0212" "0212" "0113" "0121" "0121"
#> 7th-C36_S61 7th-C3_S1 7th-C40_S70 7th-C44_S76 7th-C45_S77 7th-C47_S81 7th-C49_S4
#> "0112" "0212" "01222" "0123" "0111" "0222" "0222"
#> 7th-C4_S8 7th-C50_S5 7th-C52_S9 7th-C53_S10 7th-C56_S15 7th-C57_S16 7th-C58_S20
#> "0212" "0113" "0212" "0111" "0123" "0212" "0112"
#> 7th-C59_S21 7th-C60_S22 7th-C62_S27 7th-C64_S31 7th-C65_S32 7th-C66_S33 7th-C68_S38
#> "0111" "0212" "0111" "0111" "0211" "0113" "0123"
#> 7th-C69_S39 7th-C72_S42 7th-C73_S47 7th-C76_S52 7th-C77_S51 7th-C79_S58 7th-C80_S57
#> "0121" "0124" "0113" "023" "0111" "0112" "0113"
#> 7th-C81_S56 7th-C82_S64 7th-C84_S62 7th-C85_S69 7th-C88_S75 7th-C89_S74 7th-C8_S13
#> "023" "0112" "0111" "0221" "0123" "0113" "0111"
#> 7th-C90_S73 7th-C94_S83 7th-C96_S82 8th-C10_S100 8th-C11_S99 8th-C18_S110 8th-C20_S116
#> "0111" "0211" "0111" "0111" "0121" "0222" "0123"
#> 8th-C21_S115 8th-C23_S121 8th-C24_S120 8th-C26_S126 8th-C28_S131 8th-C2_S85 8th-C34_S141
#> "0222" "024" "0111" "0221" "024" "0111" "0121"
#> 8th-C37_S146 8th-C38_S147 8th-C44_S155 8th-C47_S160 8th-C55_S96 8th-C57_S98 8th-C58_S101
#> "0222" "0211" "0113" "0211" "0112" "0112" "0112"
#> 8th-C59_S102 8th-C61_S107 8th-C64_S112 8th-C65_S113 8th-C67_S117 8th-C69_S119 8th-C6_S88
#> "0121" "0124" "0121" "0111" "0112" "0222" "0123"
#> 8th-C70_S123 8th-C73_S130 8th-C74_S129 8th-C75_S128 8th-C79_S140 8th-C7_S95 8th-C84_S143
#> "0211" "01221" "0112" "0211" "024" "0121" "0211"
#> 8th-C85_S150 8th-C87_S148 8th-C90_S152 8th-C91_S158 8th-C92_S157 8th-C94_S162 8th-C95_S161
#> "0112" "0111" "024" "0222" "0123" "024" "0121"
#> 9th-C10_S18 9th-C11_S17 9th-C13_S24 9th-C14_S23 9th-C15_S22 9th-C16_S30 9th-C17_S29
#> "0113" "0113" "0211" "0211" "0121" "0124" "0121"
#> 9th-C19_S36 9th-C1_S3 9th-C20_S35 9th-C22_S41 9th-C25_S45 9th-C28_S50 9th-C29_S51
#> "0121" "0113" "0222" "023" "0211" "0123" "0121"
#> 9th-C2_S2 9th-C30_S52 9th-C36_S59 9th-C38_S64 9th-C3_S1 9th-C40_S69 9th-C41_S70
#> "023" "0121" "01222" "0113" "0113" "0123" "0111"
#> 9th-C46_S79 9th-C49_S4 9th-C51_S6 9th-C52_S10 9th-C57_S16 9th-C59_S20 9th-C5_S8
#> "0113" "024" "0211" "024" "0112" "0212" "0121"
#> 9th-C61_S25 9th-C62_S26 9th-C64_S31 9th-C65_S32 9th-C66_S33 9th-C67_S37 9th-C69_S39
#> "01221" "0121" "0121" "0124" "0123" "0121" "0212"
#> 9th-C6_S7 9th-C70_S42 9th-C74_S48 9th-C75_S47 9th-C77_S53 9th-C79_S57 9th-C80_S56
#> "0113" "0111" "0121" "024" "0121" "024" "0112"
#> 9th-C81_S55 9th-C83_S61 9th-C84_S60 9th-C85_S68 9th-C86_S67 9th-C87_S66 9th-C88_S73
#> "0113" "0112" "01223" "0222" "0113" "0221" "0211"
#> 9th-C89_S72 9th-C8_S14 9th-C91_S78 9th-C92_S77 9th-C93_S76 9th-C94_S83 9th-C96_S81
#> "0113" "0113" "0212" "024" "0113" "0212" "01222"
#> 9th-C9_S13
#> "0112"
get_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 903))
#> 10th_C10_S104 10th_C11_S96 10th_C13_S61 10th_C14_S53 10th_C16_S105 10th_C17_S97 10th_C19_S62
#> "0123" "0211" "0111" "0124" "0123" "0211" "0113"
#> 10th_C1_S59 10th_C20_S54 10th_C23_S98 10th_C24_S90 10th_C28_S91 10th_C30_S107 10th_C31_S48
#> "0124" "0124" "0123" "0123" "0222" "0121" "0121"
#> 10th_C32_S56 10th_C33_S64 10th_C34_S92 10th_C37_S49 10th_C41_S101 10th_C42_S109 10th_C43_S50
#> "0211" "0211" "024" "0211" "0123" "023" "0221"
#> 10th_C45_S66 10th_C46_S94 10th_C4_S103 10th_C50_S73 10th_C51_S80 10th_C52_S110 10th_C53_S118
#> "0121" "0122" "0122" "024" "0221" "024" "0221"
#> 10th_C54_S124 10th_C56_S74 10th_C57_S81 10th_C58_S111 10th_C5_S95 10th_C61_S68 10th_C63_S82
#> "0123" "0122" "0222" "0222" "0221" "0211" "023"
#> 10th_C64_S112 10th_C66_S126 10th_C68_S75 10th_C6_S88 10th_C73_S84 10th_C74_S76 10th_C76_S128
#> "0211" "0211" "0123" "0222" "0122" "0121" "0124"
#> 10th_C77_S120 10th_C78_S114 10th_C7_S60 10th_C80_S77 10th_C81_S70 10th_C84_S115 10th_C85_S86
#> "023" "0222" "0122" "023" "0113" "0113" "0124"
#> 10th_C86_S78 10th_C87_S71 10th_C88_S130 10th_C8_S52 10th_C90_S116 10th_C95_S123 10th_C96_S117
#> "023" "023" "0122" "0123" "0121" "024" "0121"
#> 11th-C10_S63 11th-C12_S47 11th-C16_S64 11th-C21_S4 11th-C22_S65 11th-C24_S49 11th-C26_S12
#> "0222" "024" "0123" "0212" "0211" "0122" "023"
#> 11th-C27_S19 11th-C2_S8 11th-C30_S66 11th-C33_S20 11th-C36_S67 11th-C37_S6 11th-C39_S21
#> "0212" "023" "0222" "0123" "0123" "0221" "0123"
#> 11th-C40_S52 11th-C41_S60 11th-C43_S7 11th-C44_S15 11th-C49_S23 11th-C4_S62 11th-C51_S39
#> "0122" "0113" "023" "0113" "0113" "023" "0113"
#> 11th-C53_S78 11th-C54_S86 11th-C55_S24 11th-C56_S32 11th-C57_S40 11th-C58_S71 11th-C5_S54
#> "0113" "0212" "023" "023" "024" "0122" "0121"
#> 11th-C61_S25 11th-C62_S33 11th-C64_S72 11th-C66_S88 11th-C67_S26 11th-C68_S34 11th-C77_S82
#> "0123" "0222" "023" "0111" "0221" "0122" "023"
#> 11th-C7_S16 11th-C93_S30 12th-C10_S155 12th-C11_S147 12th-C12_S139 12th-C14_S190 12th-C15_S183
#> "0113" "0222" "0211" "0121" "0124" "0113" "0211"
#> 12th-C1_S195 12th-C20_S191 12th-C21_S184 12th-C23_S149 12th-C24_S141 12th-C25_S185 12th-C26_S192
#> "0221" "0123" "0211" "0221" "0113" "0124" "0124"
#> 12th-C28_S142 12th-C29_S150 12th-C30_S157 12th-C33_S200 12th-C35_S151 12th-C36_S158 12th-C37_S187
#> "0121" "0112" "0124" "0124" "0211" "023" "0222"
#> 12th-C38_S194 12th-C39_S201 12th-C3_S181 12th-C40_S144 12th-C42_S159 12th-C46_S145 12th-C47_S153
#> "0211" "0221" "0211" "0221" "0113" "0122" "0211"
#> 12th-C48_S160 12th-C4_S154 12th-C50_S210 12th-C51_S217 12th-C53_S168 12th-C55_S203 12th-C56_S211
#> "0124" "0221" "024" "0124" "023" "0113" "023"
#> 12th-C57_S218 12th-C58_S162 12th-C59_S169 12th-C60_S176 12th-C63_S219 12th-C64_S163 12th-C65_S170
#> "024" "0112" "0111" "0111" "0121" "0111" "0113"
#> 12th-C67_S205 12th-C69_S135 12th-C71_S171 12th-C74_S214 12th-C75_S206 12th-C76_S177 12th-C7_S196
#> "0212" "0122" "0221" "0111" "0221" "0111" "0113"
#> 12th-C80_S215 12th-C81_S207 12th-C84_S165 12th-C85_S137 12th-C8_S189 12th-C90_S166 12th-C93_S209
#> "0121" "0121" "0111" "0123" "0221" "0113" "0212"
#> 12th-C94_S180 12th-C95_S174 12th-C96_S167 13th_C12_S178 13th_C13_S149 13th_C15_S134 13th_C16_S193
#> "0122" "0112" "0111" "0124" "0121" "0212" "0124"
#> 13th_C17_S186 13th_C18_S179 13th_C1_S147 13th_C20_S142 13th_C21_S135 13th_C23_S187 13th_C27_S151
#> "0222" "0222" "0221" "0221" "0222" "0122" "023"
#> 13th_C29_S188 13th_C31_S137 13th_C34_S181 13th_C36_S196 13th_C38_S145 13th_C39_S153 13th_C3_S132
#> "0221" "0222" "0113" "023" "0221" "0124" "0221"
#> 13th_C46_S183 13th_C49_S155 13th_C4_S191 13th_C51_S170 13th_C52_S198 13th_C53_S205 13th_C54_S212
#> "0221" "023" "0221" "0222" "0222" "0221" "0221"
#> 13th_C55_S156 13th_C57_S171 13th_C5_S184 13th_C60_S213 13th_C63_S172 13th_C66_S214 13th_C68_S165
#> "0222" "0211" "0222" "0121" "0222" "0112" "0222"
#> 13th_C69_S173 13th_C6_S177 13th_C70_S201 13th_C71_S208 13th_C72_S215 13th_C75_S159 13th_C76_S216
#> "0222" "0221" "0222" "0222" "023" "0211" "0112"
#> 13th_C77_S209 13th_C79_S174 13th_C80_S167 13th_C81_S160 13th_C86_S168 13th_C88_S218 13th_C89_S211
#> "0221" "0222" "0212" "0212" "0221" "0222" "0222"
#> 13th_C8_S140 13th_C92_S169 13th_C93_S162 13th_C94_S219 13th_C96_S204 1st-61_S27 1st-C11_S58
#> "023" "0221" "0221" "0124" "0124" "0111" "0111"
#> 1st-C13_S19 1st-C15_S3 1st-C18_S51 1st-C19_S20 1st-C20_S12 1st-C21_S4 1st-C32_S14
#> "0212" "0222" "024" "0112" "024" "0121" "0113"
#> 1st-C34_S54 1st-C39_S23 1st-C42_S71 1st-C50_S33 1st-C51_S41 1st-C53_S74 1st-C56_S34
#> "0122" "0212" "0113" "0112" "024" "024" "0112"
#> 1st-C57_S42 1st-C58_S76 1st-C59_S77 1st-C62_S35 1st-C64_S79 1st-C68_S36 1st-C69_S44
#> "0112" "0111" "024" "024" "0111" "0112" "0124"
#> 1st-C71_S83 1st-C73_S45 1st-C74_S37 1st-C75_S29 1st-C77_S86 1st-C78_S85 1st-C79_S46
#> "0121" "0112" "024" "0112" "0113" "0112" "0212"
#> 1st-C80_S38 1st-C8_S10 1st-C90_S91 1st-C96_S94 2nd-C11_S20 2nd-C15_S25 2nd-C16_S33
#> "0112" "024" "0111" "0211" "0112" "0111" "0112"
#> 2nd-C17_S32 2nd-C19_S39 2nd-C1_S3 2nd-C21_S37 2nd-C25_S49 2nd-C26_S50 2nd-C27_S51
#> "0111" "0212" "0222" "0113" "0123" "0112" "0212"
#> 2nd-C28_S55 2nd-C29_S56 2nd-C2_S2 2nd-C31_S61 2nd-C32_S62 2nd-C36_S69 2nd-C37_S73
#> "024" "0121" "023" "0121" "0111" "024" "0211"
#> 2nd-C38_S74 2nd-C39_S75 2nd-C3_S1 2nd-C47_S92 2nd-C49_S4 2nd-C4_S9 2nd-C51_S6
#> "0111" "0112" "024" "0121" "0211" "024" "0212"
#> 2nd-C52_S10 2nd-C54_S12 2nd-C57_S18 2nd-C58_S22 2nd-C5_S8 2nd-C62_S29 2nd-C67_S40
#> "0212" "0122" "0121" "024" "0212" "0111" "0112"
#> 2nd-C69_S42 2nd-C6_S7 2nd-C72_S48 2nd-C74_S53 2nd-C75_S52 2nd-C76_S60 2nd-C77_S59
#> "0222" "0121" "0111" "0121" "0112" "0123" "0112"
#> 2nd-C7_S15 2nd-C80_S65 2nd-C81_S64 2nd-C83_S71 2nd-C86_S77 2nd-C87_S76 2nd-C88_S84
#> "0212" "0112" "0124" "0121" "0113" "0211" "0111"
#> 2nd-C8_S14 2nd-C93_S88 2nd-C94_S96 2nd-C95_S95 3rd-C11_S58 3rd-C12_S68 3rd-C18_S80
#> "0112" "0111" "0222" "0113" "0111" "0112" "0121"
#> 3rd-C1_S39 3rd-C20_S22 3rd-C21_S11 3rd-C23_S94 3rd-C25_S15 3rd-C26_S28 3rd-C27_S49
#> "0123" "0123" "0121" "024" "0212" "0121" "0112"
#> 3rd-C32_S31 3rd-C33_S50 3rd-C35_S23 3rd-C36_S2 3rd-C3_S2 3rd-C40_S57 3rd-C42_S74
#> "024" "0111" "0113" "0111" "024" "0124" "0122"
#> 3rd-C44_S32 3rd-C46_S93 3rd-C47_S35 3rd-C49_S60 3rd-C4_S25 3rd-C51_S87 3rd-C52_S86
#> "024" "0123" "0112" "0112" "0111" "023" "024"
#> 3rd-C53_S67 3rd-C56_S90 3rd-C57_S5 3rd-C58_S3 3rd-C59_S91 3rd-C60_S10 3rd-C61_S64
#> "0111" "0212" "0112" "0111" "0111" "0211" "024"
#> 3rd-C63_S54 3rd-C65_S20 3rd-C67_S69 3rd-C68_S13 3rd-C69_S78 3rd-C6_S44 3rd-C71_S80
#> "024" "0113" "0121" "0124" "024" "0113" "0111"
#> 3rd-C76_S22 3rd-C79_S67 3rd-C7_S40 3rd-C82_S11 3rd-C84_S75 3rd-C85_S79 3rd-C85_S83
#> "0121" "0112" "024" "0111" "0111" "0112" "024"
#> 3rd-C86_S85 3rd-C87_S88 3rd-C88_S24 3rd-C91_S91 3rd-C92_S86 3rd-C95_S81 3rd-C96_S79
#> "0124" "0123" "0111" "0112" "0111" "0112" "0212"
#> 3rd-C9_S5 4th-61_S28 4th-C12_S19 4th-C14_S26 4th-C18_S31 4th-C22_S45 4th-C23_S44
#> "0113" "0111" "0121" "0111" "0112" "024" "0121"
#> 4th-C24_S43 4th-C26_S50 4th-C27_S51 4th-C28_S55 4th-C29_S56 4th-C32_S62 4th-C33_S63
#> "0111" "0111" "023" "0124" "0121" "0124" "0121"
#> 4th-C35_S68 4th-C36_S69 4th-C37_S73 4th-C3_S1 4th-C40_S79 4th-C43_S85 4th-C45_S87
#> "024" "0113" "024" "024" "0112" "0123" "0212"
#> 4th-C49_S4 4th-C4_S9 4th-C50_S5 4th-C51_S6 4th-C56_S17 4th-C57_S18 4th-C59_S23
#> "0124" "0112" "024" "0121" "0112" "024" "0121"
#> 4th-C5_S8 4th-C62_S29 4th-C63_S30 4th-C64_S34 4th-C66_S36 4th-C67_S40 4th-C68_S41
#> "0111" "0112" "0121" "0112" "0112" "0113" "0222"
#> 4th-C69_S42 4th-C70_S46 4th-C73_S54 4th-C75_S52 4th-C78_S58 4th-C79_S66 4th-C7_S15
#> "0121" "0123" "0112" "0112" "0122" "0112" "0111"
#> 4th-C80_S65 4th-C81_S64 4th-C82_S72 4th-C83_S71 4th-C85_S78 4th-C86_S77 4th-C87_S76
#> "0112" "0122" "0112" "0112" "0111" "0112" "0124"
#> 4th-C88_S84 4th-C89_S83 4th-C8_S14 4th-C92_S89 4th-C93_S88 4th-C94_S96 4th-C95_S95
#> "0112" "0111" "0124" "0112" "0212" "0112" "0122"
#> 4th-C96_S94 4th-C9_S13 5th-C10_S92 5th-C11_S91 5th-C12_S90 5th-C14_S97 5th-C16_S98
#> "0112" "024" "023" "023" "0123" "0211" "023"
#> 5th-C18_S96 5th-C19_S104 5th-C21_S102 5th-C25_S108 5th-C30_S105 5th-C34_S108 5th-C35_S109
#> "0211" "0122" "0121" "023" "0122" "0112" "0113"
#> 5th-C40_S112 5th-C41_S113 5th-C42_S114 5th-C43_S121 5th-C45_S123 5th-C47_S118 5th-C49_S89
#> "023" "0222" "023" "023" "023" "0122" "0111"
#> 5th-C50_S90 5th-C54_S89 5th-C56_S95 5th-C57_S96 5th-C58_S93 5th-C59_S94 5th-C5_S85
#> "0122" "0122" "023" "0122" "023" "0122" "0111"
#> 5th-C64_S99 5th-C66_S101 5th-C67_S105 5th-C68_S106 5th-C69_S107 5th-C6_S84 5th-C70_S103
#> "0122" "0122" "023" "0122" "0122" "024" "024"
#> 5th-C73_S111 5th-C74_S110 5th-C77_S107 5th-C7_S93 5th-C80_S116 5th-C81_S115 5th-C83_S111
#> "023" "0122" "0122" "0111" "0212" "023" "0222"
#> 5th-C87_S119 5th-C88_S117 5th-C90_S115 5th-C92_S124 5th-C9_S92 6th-C12_S18 6th-C15_S22
#> "024" "023" "0113" "0122" "0112" "0111" "0211"
#> 6th-C16_S29 6th-C19_S35 6th-C1_S3 6th-C20_S34 6th-C21_S33 6th-C22_S39 6th-C23_S38
#> "0124" "0212" "0211" "0113" "0112" "0113" "0111"
#> 6th-C24_S37 6th-C25_S43 6th-C28_S49 6th-C29_S50 6th-C2_S2 6th-C30_S51 6th-C34_S61
#> "0113" "0212" "0212" "0111" "0113" "0113" "0221"
#> 6th-C40_S73 6th-C42_S75 6th-C45_S81 6th-C51_S6 6th-C53_S10 6th-C54_S11 6th-C57_S17
#> "0113" "0113" "0221" "0113" "0123" "0111" "0211"
#> 6th-C58_S20 6th-C59_S21 6th-C5_S8 6th-C62_S25 6th-C63_S26 6th-C64_S30 6th-C65_S31
#> "0211" "0111" "0121" "0212" "0111" "0211" "0121"
#> 6th-C66_S32 6th-C67_S36 6th-C71_S41 6th-C73_S48 6th-C75_S46 6th-C77_S53 6th-C79_S60
#> "0113" "0212" "0111" "0113" "0113" "0111" "0111"
#> 6th-C80_S59 6th-C82_S66 6th-C83_S65 6th-C84_S64 6th-C85_S72 6th-C87_S70 6th-C89_S77
#> "0113" "0211" "024" "0211" "0111" "0112" "0212"
#> 6th-C90_S76 6th-C91_S84 6th-C93_S82 6th-C9_S12 7th-C10_S19 7th-C11_S18 7th-C12_S17
#> "0211" "0124" "0124" "0221" "0113" "0112" "0212"
#> 7th-C14_S24 7th-C15_S23 7th-C17_S29 7th-C19_S36 7th-C1_S3 7th-C20_S35 7th-C21_S34
#> "0112" "0124" "0123" "0211" "0211" "0212" "0211"
#> 7th-C24_S40 7th-C25_S43 7th-C28_S48 7th-C2_S2 7th-C31_S53 7th-C32_S54 7th-C34_S59
#> "0112" "0111" "0212" "0212" "0113" "0121" "0121"
#> 7th-C36_S61 7th-C3_S1 7th-C40_S70 7th-C44_S76 7th-C45_S77 7th-C47_S81 7th-C49_S4
#> "0112" "0212" "0122" "0123" "0111" "0222" "0222"
#> 7th-C4_S8 7th-C50_S5 7th-C52_S9 7th-C53_S10 7th-C56_S15 7th-C57_S16 7th-C58_S20
#> "0212" "0113" "0212" "0111" "0123" "0212" "0112"
#> 7th-C59_S21 7th-C60_S22 7th-C62_S27 7th-C64_S31 7th-C65_S32 7th-C66_S33 7th-C68_S38
#> "0111" "0212" "0111" "0111" "0211" "0113" "0123"
#> 7th-C69_S39 7th-C72_S42 7th-C73_S47 7th-C76_S52 7th-C77_S51 7th-C79_S58 7th-C80_S57
#> "0121" "0124" "0113" "023" "0111" "0112" "0113"
#> 7th-C81_S56 7th-C82_S64 7th-C84_S62 7th-C85_S69 7th-C88_S75 7th-C89_S74 7th-C8_S13
#> "023" "0112" "0111" "0221" "0123" "0113" "0111"
#> 7th-C90_S73 7th-C94_S83 7th-C96_S82 8th-C10_S100 8th-C11_S99 8th-C18_S110 8th-C20_S116
#> "0111" "0211" "0111" "0111" "0121" "0222" "0123"
#> 8th-C21_S115 8th-C23_S121 8th-C24_S120 8th-C26_S126 8th-C28_S131 8th-C2_S85 8th-C34_S141
#> "0222" "024" "0111" "0221" "024" "0111" "0121"
#> 8th-C37_S146 8th-C38_S147 8th-C44_S155 8th-C47_S160 8th-C55_S96 8th-C57_S98 8th-C58_S101
#> "0222" "0211" "0113" "0211" "0112" "0112" "0112"
#> 8th-C59_S102 8th-C61_S107 8th-C64_S112 8th-C65_S113 8th-C67_S117 8th-C69_S119 8th-C6_S88
#> "0121" "0124" "0121" "0111" "0112" "0222" "0123"
#> 8th-C70_S123 8th-C73_S130 8th-C74_S129 8th-C75_S128 8th-C79_S140 8th-C7_S95 8th-C84_S143
#> "0211" "0122" "0112" "0211" "024" "0121" "0211"
#> 8th-C85_S150 8th-C87_S148 8th-C90_S152 8th-C91_S158 8th-C92_S157 8th-C94_S162 8th-C95_S161
#> "0112" "0111" "024" "0222" "0123" "024" "0121"
#> 9th-C10_S18 9th-C11_S17 9th-C13_S24 9th-C14_S23 9th-C15_S22 9th-C16_S30 9th-C17_S29
#> "0113" "0113" "0211" "0211" "0121" "0124" "0121"
#> 9th-C19_S36 9th-C1_S3 9th-C20_S35 9th-C22_S41 9th-C25_S45 9th-C28_S50 9th-C29_S51
#> "0121" "0113" "0222" "023" "0211" "0123" "0121"
#> 9th-C2_S2 9th-C30_S52 9th-C36_S59 9th-C38_S64 9th-C3_S1 9th-C40_S69 9th-C41_S70
#> "023" "0121" "0122" "0113" "0113" "0123" "0111"
#> 9th-C46_S79 9th-C49_S4 9th-C51_S6 9th-C52_S10 9th-C57_S16 9th-C59_S20 9th-C5_S8
#> "0113" "024" "0211" "024" "0112" "0212" "0121"
#> 9th-C61_S25 9th-C62_S26 9th-C64_S31 9th-C65_S32 9th-C66_S33 9th-C67_S37 9th-C69_S39
#> "0122" "0121" "0121" "0124" "0123" "0121" "0212"
#> 9th-C6_S7 9th-C70_S42 9th-C74_S48 9th-C75_S47 9th-C77_S53 9th-C79_S57 9th-C80_S56
#> "0113" "0111" "0121" "024" "0121" "024" "0112"
#> 9th-C81_S55 9th-C83_S61 9th-C84_S60 9th-C85_S68 9th-C86_S67 9th-C87_S66 9th-C88_S73
#> "0113" "0112" "0122" "0222" "0113" "0221" "0211"
#> 9th-C89_S72 9th-C8_S14 9th-C91_S78 9th-C92_S77 9th-C93_S76 9th-C94_S83 9th-C96_S81
#> "0113" "0113" "0212" "024" "0113" "0212" "0122"
#> 9th-C9_S13
#> "0112"
get_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 1013))
#> 10th_C10_S104 10th_C11_S96 10th_C13_S61 10th_C14_S53 10th_C16_S105 10th_C17_S97 10th_C19_S62
#> "0123" "0211" "0111" "0124" "0123" "0211" "0113"
#> 10th_C1_S59 10th_C20_S54 10th_C23_S98 10th_C24_S90 10th_C28_S91 10th_C30_S107 10th_C31_S48
#> "0124" "0124" "0123" "0123" "022" "0121" "0121"
#> 10th_C32_S56 10th_C33_S64 10th_C34_S92 10th_C37_S49 10th_C41_S101 10th_C42_S109 10th_C43_S50
#> "0211" "0211" "024" "0211" "0123" "023" "022"
#> 10th_C45_S66 10th_C46_S94 10th_C4_S103 10th_C50_S73 10th_C51_S80 10th_C52_S110 10th_C53_S118
#> "0121" "0122" "0122" "024" "022" "024" "022"
#> 10th_C54_S124 10th_C56_S74 10th_C57_S81 10th_C58_S111 10th_C5_S95 10th_C61_S68 10th_C63_S82
#> "0123" "0122" "022" "022" "022" "0211" "023"
#> 10th_C64_S112 10th_C66_S126 10th_C68_S75 10th_C6_S88 10th_C73_S84 10th_C74_S76 10th_C76_S128
#> "0211" "0211" "0123" "022" "0122" "0121" "0124"
#> 10th_C77_S120 10th_C78_S114 10th_C7_S60 10th_C80_S77 10th_C81_S70 10th_C84_S115 10th_C85_S86
#> "023" "022" "0122" "023" "0113" "0113" "0124"
#> 10th_C86_S78 10th_C87_S71 10th_C88_S130 10th_C8_S52 10th_C90_S116 10th_C95_S123 10th_C96_S117
#> "023" "023" "0122" "0123" "0121" "024" "0121"
#> 11th-C10_S63 11th-C12_S47 11th-C16_S64 11th-C21_S4 11th-C22_S65 11th-C24_S49 11th-C26_S12
#> "022" "024" "0123" "0212" "0211" "0122" "023"
#> 11th-C27_S19 11th-C2_S8 11th-C30_S66 11th-C33_S20 11th-C36_S67 11th-C37_S6 11th-C39_S21
#> "0212" "023" "022" "0123" "0123" "022" "0123"
#> 11th-C40_S52 11th-C41_S60 11th-C43_S7 11th-C44_S15 11th-C49_S23 11th-C4_S62 11th-C51_S39
#> "0122" "0113" "023" "0113" "0113" "023" "0113"
#> 11th-C53_S78 11th-C54_S86 11th-C55_S24 11th-C56_S32 11th-C57_S40 11th-C58_S71 11th-C5_S54
#> "0113" "0212" "023" "023" "024" "0122" "0121"
#> 11th-C61_S25 11th-C62_S33 11th-C64_S72 11th-C66_S88 11th-C67_S26 11th-C68_S34 11th-C77_S82
#> "0123" "022" "023" "0111" "022" "0122" "023"
#> 11th-C7_S16 11th-C93_S30 12th-C10_S155 12th-C11_S147 12th-C12_S139 12th-C14_S190 12th-C15_S183
#> "0113" "022" "0211" "0121" "0124" "0113" "0211"
#> 12th-C1_S195 12th-C20_S191 12th-C21_S184 12th-C23_S149 12th-C24_S141 12th-C25_S185 12th-C26_S192
#> "022" "0123" "0211" "022" "0113" "0124" "0124"
#> 12th-C28_S142 12th-C29_S150 12th-C30_S157 12th-C33_S200 12th-C35_S151 12th-C36_S158 12th-C37_S187
#> "0121" "0112" "0124" "0124" "0211" "023" "022"
#> 12th-C38_S194 12th-C39_S201 12th-C3_S181 12th-C40_S144 12th-C42_S159 12th-C46_S145 12th-C47_S153
#> "0211" "022" "0211" "022" "0113" "0122" "0211"
#> 12th-C48_S160 12th-C4_S154 12th-C50_S210 12th-C51_S217 12th-C53_S168 12th-C55_S203 12th-C56_S211
#> "0124" "022" "024" "0124" "023" "0113" "023"
#> 12th-C57_S218 12th-C58_S162 12th-C59_S169 12th-C60_S176 12th-C63_S219 12th-C64_S163 12th-C65_S170
#> "024" "0112" "0111" "0111" "0121" "0111" "0113"
#> 12th-C67_S205 12th-C69_S135 12th-C71_S171 12th-C74_S214 12th-C75_S206 12th-C76_S177 12th-C7_S196
#> "0212" "0122" "022" "0111" "022" "0111" "0113"
#> 12th-C80_S215 12th-C81_S207 12th-C84_S165 12th-C85_S137 12th-C8_S189 12th-C90_S166 12th-C93_S209
#> "0121" "0121" "0111" "0123" "022" "0113" "0212"
#> 12th-C94_S180 12th-C95_S174 12th-C96_S167 13th_C12_S178 13th_C13_S149 13th_C15_S134 13th_C16_S193
#> "0122" "0112" "0111" "0124" "0121" "0212" "0124"
#> 13th_C17_S186 13th_C18_S179 13th_C1_S147 13th_C20_S142 13th_C21_S135 13th_C23_S187 13th_C27_S151
#> "022" "022" "022" "022" "022" "0122" "023"
#> 13th_C29_S188 13th_C31_S137 13th_C34_S181 13th_C36_S196 13th_C38_S145 13th_C39_S153 13th_C3_S132
#> "022" "022" "0113" "023" "022" "0124" "022"
#> 13th_C46_S183 13th_C49_S155 13th_C4_S191 13th_C51_S170 13th_C52_S198 13th_C53_S205 13th_C54_S212
#> "022" "023" "022" "022" "022" "022" "022"
#> 13th_C55_S156 13th_C57_S171 13th_C5_S184 13th_C60_S213 13th_C63_S172 13th_C66_S214 13th_C68_S165
#> "022" "0211" "022" "0121" "022" "0112" "022"
#> 13th_C69_S173 13th_C6_S177 13th_C70_S201 13th_C71_S208 13th_C72_S215 13th_C75_S159 13th_C76_S216
#> "022" "022" "022" "022" "023" "0211" "0112"
#> 13th_C77_S209 13th_C79_S174 13th_C80_S167 13th_C81_S160 13th_C86_S168 13th_C88_S218 13th_C89_S211
#> "022" "022" "0212" "0212" "022" "022" "022"
#> 13th_C8_S140 13th_C92_S169 13th_C93_S162 13th_C94_S219 13th_C96_S204 1st-61_S27 1st-C11_S58
#> "023" "022" "022" "0124" "0124" "0111" "0111"
#> 1st-C13_S19 1st-C15_S3 1st-C18_S51 1st-C19_S20 1st-C20_S12 1st-C21_S4 1st-C32_S14
#> "0212" "022" "024" "0112" "024" "0121" "0113"
#> 1st-C34_S54 1st-C39_S23 1st-C42_S71 1st-C50_S33 1st-C51_S41 1st-C53_S74 1st-C56_S34
#> "0122" "0212" "0113" "0112" "024" "024" "0112"
#> 1st-C57_S42 1st-C58_S76 1st-C59_S77 1st-C62_S35 1st-C64_S79 1st-C68_S36 1st-C69_S44
#> "0112" "0111" "024" "024" "0111" "0112" "0124"
#> 1st-C71_S83 1st-C73_S45 1st-C74_S37 1st-C75_S29 1st-C77_S86 1st-C78_S85 1st-C79_S46
#> "0121" "0112" "024" "0112" "0113" "0112" "0212"
#> 1st-C80_S38 1st-C8_S10 1st-C90_S91 1st-C96_S94 2nd-C11_S20 2nd-C15_S25 2nd-C16_S33
#> "0112" "024" "0111" "0211" "0112" "0111" "0112"
#> 2nd-C17_S32 2nd-C19_S39 2nd-C1_S3 2nd-C21_S37 2nd-C25_S49 2nd-C26_S50 2nd-C27_S51
#> "0111" "0212" "022" "0113" "0123" "0112" "0212"
#> 2nd-C28_S55 2nd-C29_S56 2nd-C2_S2 2nd-C31_S61 2nd-C32_S62 2nd-C36_S69 2nd-C37_S73
#> "024" "0121" "023" "0121" "0111" "024" "0211"
#> 2nd-C38_S74 2nd-C39_S75 2nd-C3_S1 2nd-C47_S92 2nd-C49_S4 2nd-C4_S9 2nd-C51_S6
#> "0111" "0112" "024" "0121" "0211" "024" "0212"
#> 2nd-C52_S10 2nd-C54_S12 2nd-C57_S18 2nd-C58_S22 2nd-C5_S8 2nd-C62_S29 2nd-C67_S40
#> "0212" "0122" "0121" "024" "0212" "0111" "0112"
#> 2nd-C69_S42 2nd-C6_S7 2nd-C72_S48 2nd-C74_S53 2nd-C75_S52 2nd-C76_S60 2nd-C77_S59
#> "022" "0121" "0111" "0121" "0112" "0123" "0112"
#> 2nd-C7_S15 2nd-C80_S65 2nd-C81_S64 2nd-C83_S71 2nd-C86_S77 2nd-C87_S76 2nd-C88_S84
#> "0212" "0112" "0124" "0121" "0113" "0211" "0111"
#> 2nd-C8_S14 2nd-C93_S88 2nd-C94_S96 2nd-C95_S95 3rd-C11_S58 3rd-C12_S68 3rd-C18_S80
#> "0112" "0111" "022" "0113" "0111" "0112" "0121"
#> 3rd-C1_S39 3rd-C20_S22 3rd-C21_S11 3rd-C23_S94 3rd-C25_S15 3rd-C26_S28 3rd-C27_S49
#> "0123" "0123" "0121" "024" "0212" "0121" "0112"
#> 3rd-C32_S31 3rd-C33_S50 3rd-C35_S23 3rd-C36_S2 3rd-C3_S2 3rd-C40_S57 3rd-C42_S74
#> "024" "0111" "0113" "0111" "024" "0124" "0122"
#> 3rd-C44_S32 3rd-C46_S93 3rd-C47_S35 3rd-C49_S60 3rd-C4_S25 3rd-C51_S87 3rd-C52_S86
#> "024" "0123" "0112" "0112" "0111" "023" "024"
#> 3rd-C53_S67 3rd-C56_S90 3rd-C57_S5 3rd-C58_S3 3rd-C59_S91 3rd-C60_S10 3rd-C61_S64
#> "0111" "0212" "0112" "0111" "0111" "0211" "024"
#> 3rd-C63_S54 3rd-C65_S20 3rd-C67_S69 3rd-C68_S13 3rd-C69_S78 3rd-C6_S44 3rd-C71_S80
#> "024" "0113" "0121" "0124" "024" "0113" "0111"
#> 3rd-C76_S22 3rd-C79_S67 3rd-C7_S40 3rd-C82_S11 3rd-C84_S75 3rd-C85_S79 3rd-C85_S83
#> "0121" "0112" "024" "0111" "0111" "0112" "024"
#> 3rd-C86_S85 3rd-C87_S88 3rd-C88_S24 3rd-C91_S91 3rd-C92_S86 3rd-C95_S81 3rd-C96_S79
#> "0124" "0123" "0111" "0112" "0111" "0112" "0212"
#> 3rd-C9_S5 4th-61_S28 4th-C12_S19 4th-C14_S26 4th-C18_S31 4th-C22_S45 4th-C23_S44
#> "0113" "0111" "0121" "0111" "0112" "024" "0121"
#> 4th-C24_S43 4th-C26_S50 4th-C27_S51 4th-C28_S55 4th-C29_S56 4th-C32_S62 4th-C33_S63
#> "0111" "0111" "023" "0124" "0121" "0124" "0121"
#> 4th-C35_S68 4th-C36_S69 4th-C37_S73 4th-C3_S1 4th-C40_S79 4th-C43_S85 4th-C45_S87
#> "024" "0113" "024" "024" "0112" "0123" "0212"
#> 4th-C49_S4 4th-C4_S9 4th-C50_S5 4th-C51_S6 4th-C56_S17 4th-C57_S18 4th-C59_S23
#> "0124" "0112" "024" "0121" "0112" "024" "0121"
#> 4th-C5_S8 4th-C62_S29 4th-C63_S30 4th-C64_S34 4th-C66_S36 4th-C67_S40 4th-C68_S41
#> "0111" "0112" "0121" "0112" "0112" "0113" "022"
#> 4th-C69_S42 4th-C70_S46 4th-C73_S54 4th-C75_S52 4th-C78_S58 4th-C79_S66 4th-C7_S15
#> "0121" "0123" "0112" "0112" "0122" "0112" "0111"
#> 4th-C80_S65 4th-C81_S64 4th-C82_S72 4th-C83_S71 4th-C85_S78 4th-C86_S77 4th-C87_S76
#> "0112" "0122" "0112" "0112" "0111" "0112" "0124"
#> 4th-C88_S84 4th-C89_S83 4th-C8_S14 4th-C92_S89 4th-C93_S88 4th-C94_S96 4th-C95_S95
#> "0112" "0111" "0124" "0112" "0212" "0112" "0122"
#> 4th-C96_S94 4th-C9_S13 5th-C10_S92 5th-C11_S91 5th-C12_S90 5th-C14_S97 5th-C16_S98
#> "0112" "024" "023" "023" "0123" "0211" "023"
#> 5th-C18_S96 5th-C19_S104 5th-C21_S102 5th-C25_S108 5th-C30_S105 5th-C34_S108 5th-C35_S109
#> "0211" "0122" "0121" "023" "0122" "0112" "0113"
#> 5th-C40_S112 5th-C41_S113 5th-C42_S114 5th-C43_S121 5th-C45_S123 5th-C47_S118 5th-C49_S89
#> "023" "022" "023" "023" "023" "0122" "0111"
#> 5th-C50_S90 5th-C54_S89 5th-C56_S95 5th-C57_S96 5th-C58_S93 5th-C59_S94 5th-C5_S85
#> "0122" "0122" "023" "0122" "023" "0122" "0111"
#> 5th-C64_S99 5th-C66_S101 5th-C67_S105 5th-C68_S106 5th-C69_S107 5th-C6_S84 5th-C70_S103
#> "0122" "0122" "023" "0122" "0122" "024" "024"
#> 5th-C73_S111 5th-C74_S110 5th-C77_S107 5th-C7_S93 5th-C80_S116 5th-C81_S115 5th-C83_S111
#> "023" "0122" "0122" "0111" "0212" "023" "022"
#> 5th-C87_S119 5th-C88_S117 5th-C90_S115 5th-C92_S124 5th-C9_S92 6th-C12_S18 6th-C15_S22
#> "024" "023" "0113" "0122" "0112" "0111" "0211"
#> 6th-C16_S29 6th-C19_S35 6th-C1_S3 6th-C20_S34 6th-C21_S33 6th-C22_S39 6th-C23_S38
#> "0124" "0212" "0211" "0113" "0112" "0113" "0111"
#> 6th-C24_S37 6th-C25_S43 6th-C28_S49 6th-C29_S50 6th-C2_S2 6th-C30_S51 6th-C34_S61
#> "0113" "0212" "0212" "0111" "0113" "0113" "022"
#> 6th-C40_S73 6th-C42_S75 6th-C45_S81 6th-C51_S6 6th-C53_S10 6th-C54_S11 6th-C57_S17
#> "0113" "0113" "022" "0113" "0123" "0111" "0211"
#> 6th-C58_S20 6th-C59_S21 6th-C5_S8 6th-C62_S25 6th-C63_S26 6th-C64_S30 6th-C65_S31
#> "0211" "0111" "0121" "0212" "0111" "0211" "0121"
#> 6th-C66_S32 6th-C67_S36 6th-C71_S41 6th-C73_S48 6th-C75_S46 6th-C77_S53 6th-C79_S60
#> "0113" "0212" "0111" "0113" "0113" "0111" "0111"
#> 6th-C80_S59 6th-C82_S66 6th-C83_S65 6th-C84_S64 6th-C85_S72 6th-C87_S70 6th-C89_S77
#> "0113" "0211" "024" "0211" "0111" "0112" "0212"
#> 6th-C90_S76 6th-C91_S84 6th-C93_S82 6th-C9_S12 7th-C10_S19 7th-C11_S18 7th-C12_S17
#> "0211" "0124" "0124" "022" "0113" "0112" "0212"
#> 7th-C14_S24 7th-C15_S23 7th-C17_S29 7th-C19_S36 7th-C1_S3 7th-C20_S35 7th-C21_S34
#> "0112" "0124" "0123" "0211" "0211" "0212" "0211"
#> 7th-C24_S40 7th-C25_S43 7th-C28_S48 7th-C2_S2 7th-C31_S53 7th-C32_S54 7th-C34_S59
#> "0112" "0111" "0212" "0212" "0113" "0121" "0121"
#> 7th-C36_S61 7th-C3_S1 7th-C40_S70 7th-C44_S76 7th-C45_S77 7th-C47_S81 7th-C49_S4
#> "0112" "0212" "0122" "0123" "0111" "022" "022"
#> 7th-C4_S8 7th-C50_S5 7th-C52_S9 7th-C53_S10 7th-C56_S15 7th-C57_S16 7th-C58_S20
#> "0212" "0113" "0212" "0111" "0123" "0212" "0112"
#> 7th-C59_S21 7th-C60_S22 7th-C62_S27 7th-C64_S31 7th-C65_S32 7th-C66_S33 7th-C68_S38
#> "0111" "0212" "0111" "0111" "0211" "0113" "0123"
#> 7th-C69_S39 7th-C72_S42 7th-C73_S47 7th-C76_S52 7th-C77_S51 7th-C79_S58 7th-C80_S57
#> "0121" "0124" "0113" "023" "0111" "0112" "0113"
#> 7th-C81_S56 7th-C82_S64 7th-C84_S62 7th-C85_S69 7th-C88_S75 7th-C89_S74 7th-C8_S13
#> "023" "0112" "0111" "022" "0123" "0113" "0111"
#> 7th-C90_S73 7th-C94_S83 7th-C96_S82 8th-C10_S100 8th-C11_S99 8th-C18_S110 8th-C20_S116
#> "0111" "0211" "0111" "0111" "0121" "022" "0123"
#> 8th-C21_S115 8th-C23_S121 8th-C24_S120 8th-C26_S126 8th-C28_S131 8th-C2_S85 8th-C34_S141
#> "022" "024" "0111" "022" "024" "0111" "0121"
#> 8th-C37_S146 8th-C38_S147 8th-C44_S155 8th-C47_S160 8th-C55_S96 8th-C57_S98 8th-C58_S101
#> "022" "0211" "0113" "0211" "0112" "0112" "0112"
#> 8th-C59_S102 8th-C61_S107 8th-C64_S112 8th-C65_S113 8th-C67_S117 8th-C69_S119 8th-C6_S88
#> "0121" "0124" "0121" "0111" "0112" "022" "0123"
#> 8th-C70_S123 8th-C73_S130 8th-C74_S129 8th-C75_S128 8th-C79_S140 8th-C7_S95 8th-C84_S143
#> "0211" "0122" "0112" "0211" "024" "0121" "0211"
#> 8th-C85_S150 8th-C87_S148 8th-C90_S152 8th-C91_S158 8th-C92_S157 8th-C94_S162 8th-C95_S161
#> "0112" "0111" "024" "022" "0123" "024" "0121"
#> 9th-C10_S18 9th-C11_S17 9th-C13_S24 9th-C14_S23 9th-C15_S22 9th-C16_S30 9th-C17_S29
#> "0113" "0113" "0211" "0211" "0121" "0124" "0121"
#> 9th-C19_S36 9th-C1_S3 9th-C20_S35 9th-C22_S41 9th-C25_S45 9th-C28_S50 9th-C29_S51
#> "0121" "0113" "022" "023" "0211" "0123" "0121"
#> 9th-C2_S2 9th-C30_S52 9th-C36_S59 9th-C38_S64 9th-C3_S1 9th-C40_S69 9th-C41_S70
#> "023" "0121" "0122" "0113" "0113" "0123" "0111"
#> 9th-C46_S79 9th-C49_S4 9th-C51_S6 9th-C52_S10 9th-C57_S16 9th-C59_S20 9th-C5_S8
#> "0113" "024" "0211" "024" "0112" "0212" "0121"
#> 9th-C61_S25 9th-C62_S26 9th-C64_S31 9th-C65_S32 9th-C66_S33 9th-C67_S37 9th-C69_S39
#> "0122" "0121" "0121" "0124" "0123" "0121" "0212"
#> 9th-C6_S7 9th-C70_S42 9th-C74_S48 9th-C75_S47 9th-C77_S53 9th-C79_S57 9th-C80_S56
#> "0113" "0111" "0121" "024" "0121" "024" "0112"
#> 9th-C81_S55 9th-C83_S61 9th-C84_S60 9th-C85_S68 9th-C86_S67 9th-C87_S66 9th-C88_S73
#> "0113" "0112" "0122" "022" "0113" "022" "0211"
#> 9th-C89_S72 9th-C8_S14 9th-C91_S78 9th-C92_S77 9th-C93_S76 9th-C94_S83 9th-C96_S81
#> "0113" "0113" "0212" "024" "0113" "0212" "0122"
#> 9th-C9_S13
#> "0112"
get_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 1587))
#> 10th_C10_S104 10th_C11_S96 10th_C13_S61 10th_C14_S53 10th_C16_S105 10th_C17_S97 10th_C19_S62
#> "0123" "021" "0111" "0124" "0123" "021" "0113"
#> 10th_C1_S59 10th_C20_S54 10th_C23_S98 10th_C24_S90 10th_C28_S91 10th_C30_S107 10th_C31_S48
#> "0124" "0124" "0123" "0123" "022" "0121" "0121"
#> 10th_C32_S56 10th_C33_S64 10th_C34_S92 10th_C37_S49 10th_C41_S101 10th_C42_S109 10th_C43_S50
#> "021" "021" "024" "021" "0123" "023" "022"
#> 10th_C45_S66 10th_C46_S94 10th_C4_S103 10th_C50_S73 10th_C51_S80 10th_C52_S110 10th_C53_S118
#> "0121" "0122" "0122" "024" "022" "024" "022"
#> 10th_C54_S124 10th_C56_S74 10th_C57_S81 10th_C58_S111 10th_C5_S95 10th_C61_S68 10th_C63_S82
#> "0123" "0122" "022" "022" "022" "021" "023"
#> 10th_C64_S112 10th_C66_S126 10th_C68_S75 10th_C6_S88 10th_C73_S84 10th_C74_S76 10th_C76_S128
#> "021" "021" "0123" "022" "0122" "0121" "0124"
#> 10th_C77_S120 10th_C78_S114 10th_C7_S60 10th_C80_S77 10th_C81_S70 10th_C84_S115 10th_C85_S86
#> "023" "022" "0122" "023" "0113" "0113" "0124"
#> 10th_C86_S78 10th_C87_S71 10th_C88_S130 10th_C8_S52 10th_C90_S116 10th_C95_S123 10th_C96_S117
#> "023" "023" "0122" "0123" "0121" "024" "0121"
#> 11th-C10_S63 11th-C12_S47 11th-C16_S64 11th-C21_S4 11th-C22_S65 11th-C24_S49 11th-C26_S12
#> "022" "024" "0123" "021" "021" "0122" "023"
#> 11th-C27_S19 11th-C2_S8 11th-C30_S66 11th-C33_S20 11th-C36_S67 11th-C37_S6 11th-C39_S21
#> "021" "023" "022" "0123" "0123" "022" "0123"
#> 11th-C40_S52 11th-C41_S60 11th-C43_S7 11th-C44_S15 11th-C49_S23 11th-C4_S62 11th-C51_S39
#> "0122" "0113" "023" "0113" "0113" "023" "0113"
#> 11th-C53_S78 11th-C54_S86 11th-C55_S24 11th-C56_S32 11th-C57_S40 11th-C58_S71 11th-C5_S54
#> "0113" "021" "023" "023" "024" "0122" "0121"
#> 11th-C61_S25 11th-C62_S33 11th-C64_S72 11th-C66_S88 11th-C67_S26 11th-C68_S34 11th-C77_S82
#> "0123" "022" "023" "0111" "022" "0122" "023"
#> 11th-C7_S16 11th-C93_S30 12th-C10_S155 12th-C11_S147 12th-C12_S139 12th-C14_S190 12th-C15_S183
#> "0113" "022" "021" "0121" "0124" "0113" "021"
#> 12th-C1_S195 12th-C20_S191 12th-C21_S184 12th-C23_S149 12th-C24_S141 12th-C25_S185 12th-C26_S192
#> "022" "0123" "021" "022" "0113" "0124" "0124"
#> 12th-C28_S142 12th-C29_S150 12th-C30_S157 12th-C33_S200 12th-C35_S151 12th-C36_S158 12th-C37_S187
#> "0121" "0112" "0124" "0124" "021" "023" "022"
#> 12th-C38_S194 12th-C39_S201 12th-C3_S181 12th-C40_S144 12th-C42_S159 12th-C46_S145 12th-C47_S153
#> "021" "022" "021" "022" "0113" "0122" "021"
#> 12th-C48_S160 12th-C4_S154 12th-C50_S210 12th-C51_S217 12th-C53_S168 12th-C55_S203 12th-C56_S211
#> "0124" "022" "024" "0124" "023" "0113" "023"
#> 12th-C57_S218 12th-C58_S162 12th-C59_S169 12th-C60_S176 12th-C63_S219 12th-C64_S163 12th-C65_S170
#> "024" "0112" "0111" "0111" "0121" "0111" "0113"
#> 12th-C67_S205 12th-C69_S135 12th-C71_S171 12th-C74_S214 12th-C75_S206 12th-C76_S177 12th-C7_S196
#> "021" "0122" "022" "0111" "022" "0111" "0113"
#> 12th-C80_S215 12th-C81_S207 12th-C84_S165 12th-C85_S137 12th-C8_S189 12th-C90_S166 12th-C93_S209
#> "0121" "0121" "0111" "0123" "022" "0113" "021"
#> 12th-C94_S180 12th-C95_S174 12th-C96_S167 13th_C12_S178 13th_C13_S149 13th_C15_S134 13th_C16_S193
#> "0122" "0112" "0111" "0124" "0121" "021" "0124"
#> 13th_C17_S186 13th_C18_S179 13th_C1_S147 13th_C20_S142 13th_C21_S135 13th_C23_S187 13th_C27_S151
#> "022" "022" "022" "022" "022" "0122" "023"
#> 13th_C29_S188 13th_C31_S137 13th_C34_S181 13th_C36_S196 13th_C38_S145 13th_C39_S153 13th_C3_S132
#> "022" "022" "0113" "023" "022" "0124" "022"
#> 13th_C46_S183 13th_C49_S155 13th_C4_S191 13th_C51_S170 13th_C52_S198 13th_C53_S205 13th_C54_S212
#> "022" "023" "022" "022" "022" "022" "022"
#> 13th_C55_S156 13th_C57_S171 13th_C5_S184 13th_C60_S213 13th_C63_S172 13th_C66_S214 13th_C68_S165
#> "022" "021" "022" "0121" "022" "0112" "022"
#> 13th_C69_S173 13th_C6_S177 13th_C70_S201 13th_C71_S208 13th_C72_S215 13th_C75_S159 13th_C76_S216
#> "022" "022" "022" "022" "023" "021" "0112"
#> 13th_C77_S209 13th_C79_S174 13th_C80_S167 13th_C81_S160 13th_C86_S168 13th_C88_S218 13th_C89_S211
#> "022" "022" "021" "021" "022" "022" "022"
#> 13th_C8_S140 13th_C92_S169 13th_C93_S162 13th_C94_S219 13th_C96_S204 1st-61_S27 1st-C11_S58
#> "023" "022" "022" "0124" "0124" "0111" "0111"
#> 1st-C13_S19 1st-C15_S3 1st-C18_S51 1st-C19_S20 1st-C20_S12 1st-C21_S4 1st-C32_S14
#> "021" "022" "024" "0112" "024" "0121" "0113"
#> 1st-C34_S54 1st-C39_S23 1st-C42_S71 1st-C50_S33 1st-C51_S41 1st-C53_S74 1st-C56_S34
#> "0122" "021" "0113" "0112" "024" "024" "0112"
#> 1st-C57_S42 1st-C58_S76 1st-C59_S77 1st-C62_S35 1st-C64_S79 1st-C68_S36 1st-C69_S44
#> "0112" "0111" "024" "024" "0111" "0112" "0124"
#> 1st-C71_S83 1st-C73_S45 1st-C74_S37 1st-C75_S29 1st-C77_S86 1st-C78_S85 1st-C79_S46
#> "0121" "0112" "024" "0112" "0113" "0112" "021"
#> 1st-C80_S38 1st-C8_S10 1st-C90_S91 1st-C96_S94 2nd-C11_S20 2nd-C15_S25 2nd-C16_S33
#> "0112" "024" "0111" "021" "0112" "0111" "0112"
#> 2nd-C17_S32 2nd-C19_S39 2nd-C1_S3 2nd-C21_S37 2nd-C25_S49 2nd-C26_S50 2nd-C27_S51
#> "0111" "021" "022" "0113" "0123" "0112" "021"
#> 2nd-C28_S55 2nd-C29_S56 2nd-C2_S2 2nd-C31_S61 2nd-C32_S62 2nd-C36_S69 2nd-C37_S73
#> "024" "0121" "023" "0121" "0111" "024" "021"
#> 2nd-C38_S74 2nd-C39_S75 2nd-C3_S1 2nd-C47_S92 2nd-C49_S4 2nd-C4_S9 2nd-C51_S6
#> "0111" "0112" "024" "0121" "021" "024" "021"
#> 2nd-C52_S10 2nd-C54_S12 2nd-C57_S18 2nd-C58_S22 2nd-C5_S8 2nd-C62_S29 2nd-C67_S40
#> "021" "0122" "0121" "024" "021" "0111" "0112"
#> 2nd-C69_S42 2nd-C6_S7 2nd-C72_S48 2nd-C74_S53 2nd-C75_S52 2nd-C76_S60 2nd-C77_S59
#> "022" "0121" "0111" "0121" "0112" "0123" "0112"
#> 2nd-C7_S15 2nd-C80_S65 2nd-C81_S64 2nd-C83_S71 2nd-C86_S77 2nd-C87_S76 2nd-C88_S84
#> "021" "0112" "0124" "0121" "0113" "021" "0111"
#> 2nd-C8_S14 2nd-C93_S88 2nd-C94_S96 2nd-C95_S95 3rd-C11_S58 3rd-C12_S68 3rd-C18_S80
#> "0112" "0111" "022" "0113" "0111" "0112" "0121"
#> 3rd-C1_S39 3rd-C20_S22 3rd-C21_S11 3rd-C23_S94 3rd-C25_S15 3rd-C26_S28 3rd-C27_S49
#> "0123" "0123" "0121" "024" "021" "0121" "0112"
#> 3rd-C32_S31 3rd-C33_S50 3rd-C35_S23 3rd-C36_S2 3rd-C3_S2 3rd-C40_S57 3rd-C42_S74
#> "024" "0111" "0113" "0111" "024" "0124" "0122"
#> 3rd-C44_S32 3rd-C46_S93 3rd-C47_S35 3rd-C49_S60 3rd-C4_S25 3rd-C51_S87 3rd-C52_S86
#> "024" "0123" "0112" "0112" "0111" "023" "024"
#> 3rd-C53_S67 3rd-C56_S90 3rd-C57_S5 3rd-C58_S3 3rd-C59_S91 3rd-C60_S10 3rd-C61_S64
#> "0111" "021" "0112" "0111" "0111" "021" "024"
#> 3rd-C63_S54 3rd-C65_S20 3rd-C67_S69 3rd-C68_S13 3rd-C69_S78 3rd-C6_S44 3rd-C71_S80
#> "024" "0113" "0121" "0124" "024" "0113" "0111"
#> 3rd-C76_S22 3rd-C79_S67 3rd-C7_S40 3rd-C82_S11 3rd-C84_S75 3rd-C85_S79 3rd-C85_S83
#> "0121" "0112" "024" "0111" "0111" "0112" "024"
#> 3rd-C86_S85 3rd-C87_S88 3rd-C88_S24 3rd-C91_S91 3rd-C92_S86 3rd-C95_S81 3rd-C96_S79
#> "0124" "0123" "0111" "0112" "0111" "0112" "021"
#> 3rd-C9_S5 4th-61_S28 4th-C12_S19 4th-C14_S26 4th-C18_S31 4th-C22_S45 4th-C23_S44
#> "0113" "0111" "0121" "0111" "0112" "024" "0121"
#> 4th-C24_S43 4th-C26_S50 4th-C27_S51 4th-C28_S55 4th-C29_S56 4th-C32_S62 4th-C33_S63
#> "0111" "0111" "023" "0124" "0121" "0124" "0121"
#> 4th-C35_S68 4th-C36_S69 4th-C37_S73 4th-C3_S1 4th-C40_S79 4th-C43_S85 4th-C45_S87
#> "024" "0113" "024" "024" "0112" "0123" "021"
#> 4th-C49_S4 4th-C4_S9 4th-C50_S5 4th-C51_S6 4th-C56_S17 4th-C57_S18 4th-C59_S23
#> "0124" "0112" "024" "0121" "0112" "024" "0121"
#> 4th-C5_S8 4th-C62_S29 4th-C63_S30 4th-C64_S34 4th-C66_S36 4th-C67_S40 4th-C68_S41
#> "0111" "0112" "0121" "0112" "0112" "0113" "022"
#> 4th-C69_S42 4th-C70_S46 4th-C73_S54 4th-C75_S52 4th-C78_S58 4th-C79_S66 4th-C7_S15
#> "0121" "0123" "0112" "0112" "0122" "0112" "0111"
#> 4th-C80_S65 4th-C81_S64 4th-C82_S72 4th-C83_S71 4th-C85_S78 4th-C86_S77 4th-C87_S76
#> "0112" "0122" "0112" "0112" "0111" "0112" "0124"
#> 4th-C88_S84 4th-C89_S83 4th-C8_S14 4th-C92_S89 4th-C93_S88 4th-C94_S96 4th-C95_S95
#> "0112" "0111" "0124" "0112" "021" "0112" "0122"
#> 4th-C96_S94 4th-C9_S13 5th-C10_S92 5th-C11_S91 5th-C12_S90 5th-C14_S97 5th-C16_S98
#> "0112" "024" "023" "023" "0123" "021" "023"
#> 5th-C18_S96 5th-C19_S104 5th-C21_S102 5th-C25_S108 5th-C30_S105 5th-C34_S108 5th-C35_S109
#> "021" "0122" "0121" "023" "0122" "0112" "0113"
#> 5th-C40_S112 5th-C41_S113 5th-C42_S114 5th-C43_S121 5th-C45_S123 5th-C47_S118 5th-C49_S89
#> "023" "022" "023" "023" "023" "0122" "0111"
#> 5th-C50_S90 5th-C54_S89 5th-C56_S95 5th-C57_S96 5th-C58_S93 5th-C59_S94 5th-C5_S85
#> "0122" "0122" "023" "0122" "023" "0122" "0111"
#> 5th-C64_S99 5th-C66_S101 5th-C67_S105 5th-C68_S106 5th-C69_S107 5th-C6_S84 5th-C70_S103
#> "0122" "0122" "023" "0122" "0122" "024" "024"
#> 5th-C73_S111 5th-C74_S110 5th-C77_S107 5th-C7_S93 5th-C80_S116 5th-C81_S115 5th-C83_S111
#> "023" "0122" "0122" "0111" "021" "023" "022"
#> 5th-C87_S119 5th-C88_S117 5th-C90_S115 5th-C92_S124 5th-C9_S92 6th-C12_S18 6th-C15_S22
#> "024" "023" "0113" "0122" "0112" "0111" "021"
#> 6th-C16_S29 6th-C19_S35 6th-C1_S3 6th-C20_S34 6th-C21_S33 6th-C22_S39 6th-C23_S38
#> "0124" "021" "021" "0113" "0112" "0113" "0111"
#> 6th-C24_S37 6th-C25_S43 6th-C28_S49 6th-C29_S50 6th-C2_S2 6th-C30_S51 6th-C34_S61
#> "0113" "021" "021" "0111" "0113" "0113" "022"
#> 6th-C40_S73 6th-C42_S75 6th-C45_S81 6th-C51_S6 6th-C53_S10 6th-C54_S11 6th-C57_S17
#> "0113" "0113" "022" "0113" "0123" "0111" "021"
#> 6th-C58_S20 6th-C59_S21 6th-C5_S8 6th-C62_S25 6th-C63_S26 6th-C64_S30 6th-C65_S31
#> "021" "0111" "0121" "021" "0111" "021" "0121"
#> 6th-C66_S32 6th-C67_S36 6th-C71_S41 6th-C73_S48 6th-C75_S46 6th-C77_S53 6th-C79_S60
#> "0113" "021" "0111" "0113" "0113" "0111" "0111"
#> 6th-C80_S59 6th-C82_S66 6th-C83_S65 6th-C84_S64 6th-C85_S72 6th-C87_S70 6th-C89_S77
#> "0113" "021" "024" "021" "0111" "0112" "021"
#> 6th-C90_S76 6th-C91_S84 6th-C93_S82 6th-C9_S12 7th-C10_S19 7th-C11_S18 7th-C12_S17
#> "021" "0124" "0124" "022" "0113" "0112" "021"
#> 7th-C14_S24 7th-C15_S23 7th-C17_S29 7th-C19_S36 7th-C1_S3 7th-C20_S35 7th-C21_S34
#> "0112" "0124" "0123" "021" "021" "021" "021"
#> 7th-C24_S40 7th-C25_S43 7th-C28_S48 7th-C2_S2 7th-C31_S53 7th-C32_S54 7th-C34_S59
#> "0112" "0111" "021" "021" "0113" "0121" "0121"
#> 7th-C36_S61 7th-C3_S1 7th-C40_S70 7th-C44_S76 7th-C45_S77 7th-C47_S81 7th-C49_S4
#> "0112" "021" "0122" "0123" "0111" "022" "022"
#> 7th-C4_S8 7th-C50_S5 7th-C52_S9 7th-C53_S10 7th-C56_S15 7th-C57_S16 7th-C58_S20
#> "021" "0113" "021" "0111" "0123" "021" "0112"
#> 7th-C59_S21 7th-C60_S22 7th-C62_S27 7th-C64_S31 7th-C65_S32 7th-C66_S33 7th-C68_S38
#> "0111" "021" "0111" "0111" "021" "0113" "0123"
#> 7th-C69_S39 7th-C72_S42 7th-C73_S47 7th-C76_S52 7th-C77_S51 7th-C79_S58 7th-C80_S57
#> "0121" "0124" "0113" "023" "0111" "0112" "0113"
#> 7th-C81_S56 7th-C82_S64 7th-C84_S62 7th-C85_S69 7th-C88_S75 7th-C89_S74 7th-C8_S13
#> "023" "0112" "0111" "022" "0123" "0113" "0111"
#> 7th-C90_S73 7th-C94_S83 7th-C96_S82 8th-C10_S100 8th-C11_S99 8th-C18_S110 8th-C20_S116
#> "0111" "021" "0111" "0111" "0121" "022" "0123"
#> 8th-C21_S115 8th-C23_S121 8th-C24_S120 8th-C26_S126 8th-C28_S131 8th-C2_S85 8th-C34_S141
#> "022" "024" "0111" "022" "024" "0111" "0121"
#> 8th-C37_S146 8th-C38_S147 8th-C44_S155 8th-C47_S160 8th-C55_S96 8th-C57_S98 8th-C58_S101
#> "022" "021" "0113" "021" "0112" "0112" "0112"
#> 8th-C59_S102 8th-C61_S107 8th-C64_S112 8th-C65_S113 8th-C67_S117 8th-C69_S119 8th-C6_S88
#> "0121" "0124" "0121" "0111" "0112" "022" "0123"
#> 8th-C70_S123 8th-C73_S130 8th-C74_S129 8th-C75_S128 8th-C79_S140 8th-C7_S95 8th-C84_S143
#> "021" "0122" "0112" "021" "024" "0121" "021"
#> 8th-C85_S150 8th-C87_S148 8th-C90_S152 8th-C91_S158 8th-C92_S157 8th-C94_S162 8th-C95_S161
#> "0112" "0111" "024" "022" "0123" "024" "0121"
#> 9th-C10_S18 9th-C11_S17 9th-C13_S24 9th-C14_S23 9th-C15_S22 9th-C16_S30 9th-C17_S29
#> "0113" "0113" "021" "021" "0121" "0124" "0121"
#> 9th-C19_S36 9th-C1_S3 9th-C20_S35 9th-C22_S41 9th-C25_S45 9th-C28_S50 9th-C29_S51
#> "0121" "0113" "022" "023" "021" "0123" "0121"
#> 9th-C2_S2 9th-C30_S52 9th-C36_S59 9th-C38_S64 9th-C3_S1 9th-C40_S69 9th-C41_S70
#> "023" "0121" "0122" "0113" "0113" "0123" "0111"
#> 9th-C46_S79 9th-C49_S4 9th-C51_S6 9th-C52_S10 9th-C57_S16 9th-C59_S20 9th-C5_S8
#> "0113" "024" "021" "024" "0112" "021" "0121"
#> 9th-C61_S25 9th-C62_S26 9th-C64_S31 9th-C65_S32 9th-C66_S33 9th-C67_S37 9th-C69_S39
#> "0122" "0121" "0121" "0124" "0123" "0121" "021"
#> 9th-C6_S7 9th-C70_S42 9th-C74_S48 9th-C75_S47 9th-C77_S53 9th-C79_S57 9th-C80_S56
#> "0113" "0111" "0121" "024" "0121" "024" "0112"
#> 9th-C81_S55 9th-C83_S61 9th-C84_S60 9th-C85_S68 9th-C86_S67 9th-C87_S66 9th-C88_S73
#> "0113" "0112" "0122" "022" "0113" "022" "021"
#> 9th-C89_S72 9th-C8_S14 9th-C91_S78 9th-C92_S77 9th-C93_S76 9th-C94_S83 9th-C96_S81
#> "0113" "0113" "021" "024" "0113" "021" "0122"
#> 9th-C9_S13
#> "0112"
get_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 2764))
#> 10th_C10_S104 10th_C11_S96 10th_C13_S61 10th_C14_S53 10th_C16_S105 10th_C17_S97 10th_C19_S62
#> "01" "021" "01" "01" "01" "021" "01"
#> 10th_C1_S59 10th_C20_S54 10th_C23_S98 10th_C24_S90 10th_C28_S91 10th_C30_S107 10th_C31_S48
#> "01" "01" "01" "01" "022" "01" "01"
#> 10th_C32_S56 10th_C33_S64 10th_C34_S92 10th_C37_S49 10th_C41_S101 10th_C42_S109 10th_C43_S50
#> "021" "021" "024" "021" "01" "023" "022"
#> 10th_C45_S66 10th_C46_S94 10th_C4_S103 10th_C50_S73 10th_C51_S80 10th_C52_S110 10th_C53_S118
#> "01" "01" "01" "024" "022" "024" "022"
#> 10th_C54_S124 10th_C56_S74 10th_C57_S81 10th_C58_S111 10th_C5_S95 10th_C61_S68 10th_C63_S82
#> "01" "01" "022" "022" "022" "021" "023"
#> 10th_C64_S112 10th_C66_S126 10th_C68_S75 10th_C6_S88 10th_C73_S84 10th_C74_S76 10th_C76_S128
#> "021" "021" "01" "022" "01" "01" "01"
#> 10th_C77_S120 10th_C78_S114 10th_C7_S60 10th_C80_S77 10th_C81_S70 10th_C84_S115 10th_C85_S86
#> "023" "022" "01" "023" "01" "01" "01"
#> 10th_C86_S78 10th_C87_S71 10th_C88_S130 10th_C8_S52 10th_C90_S116 10th_C95_S123 10th_C96_S117
#> "023" "023" "01" "01" "01" "024" "01"
#> 11th-C10_S63 11th-C12_S47 11th-C16_S64 11th-C21_S4 11th-C22_S65 11th-C24_S49 11th-C26_S12
#> "022" "024" "01" "021" "021" "01" "023"
#> 11th-C27_S19 11th-C2_S8 11th-C30_S66 11th-C33_S20 11th-C36_S67 11th-C37_S6 11th-C39_S21
#> "021" "023" "022" "01" "01" "022" "01"
#> 11th-C40_S52 11th-C41_S60 11th-C43_S7 11th-C44_S15 11th-C49_S23 11th-C4_S62 11th-C51_S39
#> "01" "01" "023" "01" "01" "023" "01"
#> 11th-C53_S78 11th-C54_S86 11th-C55_S24 11th-C56_S32 11th-C57_S40 11th-C58_S71 11th-C5_S54
#> "01" "021" "023" "023" "024" "01" "01"
#> 11th-C61_S25 11th-C62_S33 11th-C64_S72 11th-C66_S88 11th-C67_S26 11th-C68_S34 11th-C77_S82
#> "01" "022" "023" "01" "022" "01" "023"
#> 11th-C7_S16 11th-C93_S30 12th-C10_S155 12th-C11_S147 12th-C12_S139 12th-C14_S190 12th-C15_S183
#> "01" "022" "021" "01" "01" "01" "021"
#> 12th-C1_S195 12th-C20_S191 12th-C21_S184 12th-C23_S149 12th-C24_S141 12th-C25_S185 12th-C26_S192
#> "022" "01" "021" "022" "01" "01" "01"
#> 12th-C28_S142 12th-C29_S150 12th-C30_S157 12th-C33_S200 12th-C35_S151 12th-C36_S158 12th-C37_S187
#> "01" "01" "01" "01" "021" "023" "022"
#> 12th-C38_S194 12th-C39_S201 12th-C3_S181 12th-C40_S144 12th-C42_S159 12th-C46_S145 12th-C47_S153
#> "021" "022" "021" "022" "01" "01" "021"
#> 12th-C48_S160 12th-C4_S154 12th-C50_S210 12th-C51_S217 12th-C53_S168 12th-C55_S203 12th-C56_S211
#> "01" "022" "024" "01" "023" "01" "023"
#> 12th-C57_S218 12th-C58_S162 12th-C59_S169 12th-C60_S176 12th-C63_S219 12th-C64_S163 12th-C65_S170
#> "024" "01" "01" "01" "01" "01" "01"
#> 12th-C67_S205 12th-C69_S135 12th-C71_S171 12th-C74_S214 12th-C75_S206 12th-C76_S177 12th-C7_S196
#> "021" "01" "022" "01" "022" "01" "01"
#> 12th-C80_S215 12th-C81_S207 12th-C84_S165 12th-C85_S137 12th-C8_S189 12th-C90_S166 12th-C93_S209
#> "01" "01" "01" "01" "022" "01" "021"
#> 12th-C94_S180 12th-C95_S174 12th-C96_S167 13th_C12_S178 13th_C13_S149 13th_C15_S134 13th_C16_S193
#> "01" "01" "01" "01" "01" "021" "01"
#> 13th_C17_S186 13th_C18_S179 13th_C1_S147 13th_C20_S142 13th_C21_S135 13th_C23_S187 13th_C27_S151
#> "022" "022" "022" "022" "022" "01" "023"
#> 13th_C29_S188 13th_C31_S137 13th_C34_S181 13th_C36_S196 13th_C38_S145 13th_C39_S153 13th_C3_S132
#> "022" "022" "01" "023" "022" "01" "022"
#> 13th_C46_S183 13th_C49_S155 13th_C4_S191 13th_C51_S170 13th_C52_S198 13th_C53_S205 13th_C54_S212
#> "022" "023" "022" "022" "022" "022" "022"
#> 13th_C55_S156 13th_C57_S171 13th_C5_S184 13th_C60_S213 13th_C63_S172 13th_C66_S214 13th_C68_S165
#> "022" "021" "022" "01" "022" "01" "022"
#> 13th_C69_S173 13th_C6_S177 13th_C70_S201 13th_C71_S208 13th_C72_S215 13th_C75_S159 13th_C76_S216
#> "022" "022" "022" "022" "023" "021" "01"
#> 13th_C77_S209 13th_C79_S174 13th_C80_S167 13th_C81_S160 13th_C86_S168 13th_C88_S218 13th_C89_S211
#> "022" "022" "021" "021" "022" "022" "022"
#> 13th_C8_S140 13th_C92_S169 13th_C93_S162 13th_C94_S219 13th_C96_S204 1st-61_S27 1st-C11_S58
#> "023" "022" "022" "01" "01" "01" "01"
#> 1st-C13_S19 1st-C15_S3 1st-C18_S51 1st-C19_S20 1st-C20_S12 1st-C21_S4 1st-C32_S14
#> "021" "022" "024" "01" "024" "01" "01"
#> 1st-C34_S54 1st-C39_S23 1st-C42_S71 1st-C50_S33 1st-C51_S41 1st-C53_S74 1st-C56_S34
#> "01" "021" "01" "01" "024" "024" "01"
#> 1st-C57_S42 1st-C58_S76 1st-C59_S77 1st-C62_S35 1st-C64_S79 1st-C68_S36 1st-C69_S44
#> "01" "01" "024" "024" "01" "01" "01"
#> 1st-C71_S83 1st-C73_S45 1st-C74_S37 1st-C75_S29 1st-C77_S86 1st-C78_S85 1st-C79_S46
#> "01" "01" "024" "01" "01" "01" "021"
#> 1st-C80_S38 1st-C8_S10 1st-C90_S91 1st-C96_S94 2nd-C11_S20 2nd-C15_S25 2nd-C16_S33
#> "01" "024" "01" "021" "01" "01" "01"
#> 2nd-C17_S32 2nd-C19_S39 2nd-C1_S3 2nd-C21_S37 2nd-C25_S49 2nd-C26_S50 2nd-C27_S51
#> "01" "021" "022" "01" "01" "01" "021"
#> 2nd-C28_S55 2nd-C29_S56 2nd-C2_S2 2nd-C31_S61 2nd-C32_S62 2nd-C36_S69 2nd-C37_S73
#> "024" "01" "023" "01" "01" "024" "021"
#> 2nd-C38_S74 2nd-C39_S75 2nd-C3_S1 2nd-C47_S92 2nd-C49_S4 2nd-C4_S9 2nd-C51_S6
#> "01" "01" "024" "01" "021" "024" "021"
#> 2nd-C52_S10 2nd-C54_S12 2nd-C57_S18 2nd-C58_S22 2nd-C5_S8 2nd-C62_S29 2nd-C67_S40
#> "021" "01" "01" "024" "021" "01" "01"
#> 2nd-C69_S42 2nd-C6_S7 2nd-C72_S48 2nd-C74_S53 2nd-C75_S52 2nd-C76_S60 2nd-C77_S59
#> "022" "01" "01" "01" "01" "01" "01"
#> 2nd-C7_S15 2nd-C80_S65 2nd-C81_S64 2nd-C83_S71 2nd-C86_S77 2nd-C87_S76 2nd-C88_S84
#> "021" "01" "01" "01" "01" "021" "01"
#> 2nd-C8_S14 2nd-C93_S88 2nd-C94_S96 2nd-C95_S95 3rd-C11_S58 3rd-C12_S68 3rd-C18_S80
#> "01" "01" "022" "01" "01" "01" "01"
#> 3rd-C1_S39 3rd-C20_S22 3rd-C21_S11 3rd-C23_S94 3rd-C25_S15 3rd-C26_S28 3rd-C27_S49
#> "01" "01" "01" "024" "021" "01" "01"
#> 3rd-C32_S31 3rd-C33_S50 3rd-C35_S23 3rd-C36_S2 3rd-C3_S2 3rd-C40_S57 3rd-C42_S74
#> "024" "01" "01" "01" "024" "01" "01"
#> 3rd-C44_S32 3rd-C46_S93 3rd-C47_S35 3rd-C49_S60 3rd-C4_S25 3rd-C51_S87 3rd-C52_S86
#> "024" "01" "01" "01" "01" "023" "024"
#> 3rd-C53_S67 3rd-C56_S90 3rd-C57_S5 3rd-C58_S3 3rd-C59_S91 3rd-C60_S10 3rd-C61_S64
#> "01" "021" "01" "01" "01" "021" "024"
#> 3rd-C63_S54 3rd-C65_S20 3rd-C67_S69 3rd-C68_S13 3rd-C69_S78 3rd-C6_S44 3rd-C71_S80
#> "024" "01" "01" "01" "024" "01" "01"
#> 3rd-C76_S22 3rd-C79_S67 3rd-C7_S40 3rd-C82_S11 3rd-C84_S75 3rd-C85_S79 3rd-C85_S83
#> "01" "01" "024" "01" "01" "01" "024"
#> 3rd-C86_S85 3rd-C87_S88 3rd-C88_S24 3rd-C91_S91 3rd-C92_S86 3rd-C95_S81 3rd-C96_S79
#> "01" "01" "01" "01" "01" "01" "021"
#> 3rd-C9_S5 4th-61_S28 4th-C12_S19 4th-C14_S26 4th-C18_S31 4th-C22_S45 4th-C23_S44
#> "01" "01" "01" "01" "01" "024" "01"
#> 4th-C24_S43 4th-C26_S50 4th-C27_S51 4th-C28_S55 4th-C29_S56 4th-C32_S62 4th-C33_S63
#> "01" "01" "023" "01" "01" "01" "01"
#> 4th-C35_S68 4th-C36_S69 4th-C37_S73 4th-C3_S1 4th-C40_S79 4th-C43_S85 4th-C45_S87
#> "024" "01" "024" "024" "01" "01" "021"
#> 4th-C49_S4 4th-C4_S9 4th-C50_S5 4th-C51_S6 4th-C56_S17 4th-C57_S18 4th-C59_S23
#> "01" "01" "024" "01" "01" "024" "01"
#> 4th-C5_S8 4th-C62_S29 4th-C63_S30 4th-C64_S34 4th-C66_S36 4th-C67_S40 4th-C68_S41
#> "01" "01" "01" "01" "01" "01" "022"
#> 4th-C69_S42 4th-C70_S46 4th-C73_S54 4th-C75_S52 4th-C78_S58 4th-C79_S66 4th-C7_S15
#> "01" "01" "01" "01" "01" "01" "01"
#> 4th-C80_S65 4th-C81_S64 4th-C82_S72 4th-C83_S71 4th-C85_S78 4th-C86_S77 4th-C87_S76
#> "01" "01" "01" "01" "01" "01" "01"
#> 4th-C88_S84 4th-C89_S83 4th-C8_S14 4th-C92_S89 4th-C93_S88 4th-C94_S96 4th-C95_S95
#> "01" "01" "01" "01" "021" "01" "01"
#> 4th-C96_S94 4th-C9_S13 5th-C10_S92 5th-C11_S91 5th-C12_S90 5th-C14_S97 5th-C16_S98
#> "01" "024" "023" "023" "01" "021" "023"
#> 5th-C18_S96 5th-C19_S104 5th-C21_S102 5th-C25_S108 5th-C30_S105 5th-C34_S108 5th-C35_S109
#> "021" "01" "01" "023" "01" "01" "01"
#> 5th-C40_S112 5th-C41_S113 5th-C42_S114 5th-C43_S121 5th-C45_S123 5th-C47_S118 5th-C49_S89
#> "023" "022" "023" "023" "023" "01" "01"
#> 5th-C50_S90 5th-C54_S89 5th-C56_S95 5th-C57_S96 5th-C58_S93 5th-C59_S94 5th-C5_S85
#> "01" "01" "023" "01" "023" "01" "01"
#> 5th-C64_S99 5th-C66_S101 5th-C67_S105 5th-C68_S106 5th-C69_S107 5th-C6_S84 5th-C70_S103
#> "01" "01" "023" "01" "01" "024" "024"
#> 5th-C73_S111 5th-C74_S110 5th-C77_S107 5th-C7_S93 5th-C80_S116 5th-C81_S115 5th-C83_S111
#> "023" "01" "01" "01" "021" "023" "022"
#> 5th-C87_S119 5th-C88_S117 5th-C90_S115 5th-C92_S124 5th-C9_S92 6th-C12_S18 6th-C15_S22
#> "024" "023" "01" "01" "01" "01" "021"
#> 6th-C16_S29 6th-C19_S35 6th-C1_S3 6th-C20_S34 6th-C21_S33 6th-C22_S39 6th-C23_S38
#> "01" "021" "021" "01" "01" "01" "01"
#> 6th-C24_S37 6th-C25_S43 6th-C28_S49 6th-C29_S50 6th-C2_S2 6th-C30_S51 6th-C34_S61
#> "01" "021" "021" "01" "01" "01" "022"
#> 6th-C40_S73 6th-C42_S75 6th-C45_S81 6th-C51_S6 6th-C53_S10 6th-C54_S11 6th-C57_S17
#> "01" "01" "022" "01" "01" "01" "021"
#> 6th-C58_S20 6th-C59_S21 6th-C5_S8 6th-C62_S25 6th-C63_S26 6th-C64_S30 6th-C65_S31
#> "021" "01" "01" "021" "01" "021" "01"
#> 6th-C66_S32 6th-C67_S36 6th-C71_S41 6th-C73_S48 6th-C75_S46 6th-C77_S53 6th-C79_S60
#> "01" "021" "01" "01" "01" "01" "01"
#> 6th-C80_S59 6th-C82_S66 6th-C83_S65 6th-C84_S64 6th-C85_S72 6th-C87_S70 6th-C89_S77
#> "01" "021" "024" "021" "01" "01" "021"
#> 6th-C90_S76 6th-C91_S84 6th-C93_S82 6th-C9_S12 7th-C10_S19 7th-C11_S18 7th-C12_S17
#> "021" "01" "01" "022" "01" "01" "021"
#> 7th-C14_S24 7th-C15_S23 7th-C17_S29 7th-C19_S36 7th-C1_S3 7th-C20_S35 7th-C21_S34
#> "01" "01" "01" "021" "021" "021" "021"
#> 7th-C24_S40 7th-C25_S43 7th-C28_S48 7th-C2_S2 7th-C31_S53 7th-C32_S54 7th-C34_S59
#> "01" "01" "021" "021" "01" "01" "01"
#> 7th-C36_S61 7th-C3_S1 7th-C40_S70 7th-C44_S76 7th-C45_S77 7th-C47_S81 7th-C49_S4
#> "01" "021" "01" "01" "01" "022" "022"
#> 7th-C4_S8 7th-C50_S5 7th-C52_S9 7th-C53_S10 7th-C56_S15 7th-C57_S16 7th-C58_S20
#> "021" "01" "021" "01" "01" "021" "01"
#> 7th-C59_S21 7th-C60_S22 7th-C62_S27 7th-C64_S31 7th-C65_S32 7th-C66_S33 7th-C68_S38
#> "01" "021" "01" "01" "021" "01" "01"
#> 7th-C69_S39 7th-C72_S42 7th-C73_S47 7th-C76_S52 7th-C77_S51 7th-C79_S58 7th-C80_S57
#> "01" "01" "01" "023" "01" "01" "01"
#> 7th-C81_S56 7th-C82_S64 7th-C84_S62 7th-C85_S69 7th-C88_S75 7th-C89_S74 7th-C8_S13
#> "023" "01" "01" "022" "01" "01" "01"
#> 7th-C90_S73 7th-C94_S83 7th-C96_S82 8th-C10_S100 8th-C11_S99 8th-C18_S110 8th-C20_S116
#> "01" "021" "01" "01" "01" "022" "01"
#> 8th-C21_S115 8th-C23_S121 8th-C24_S120 8th-C26_S126 8th-C28_S131 8th-C2_S85 8th-C34_S141
#> "022" "024" "01" "022" "024" "01" "01"
#> 8th-C37_S146 8th-C38_S147 8th-C44_S155 8th-C47_S160 8th-C55_S96 8th-C57_S98 8th-C58_S101
#> "022" "021" "01" "021" "01" "01" "01"
#> 8th-C59_S102 8th-C61_S107 8th-C64_S112 8th-C65_S113 8th-C67_S117 8th-C69_S119 8th-C6_S88
#> "01" "01" "01" "01" "01" "022" "01"
#> 8th-C70_S123 8th-C73_S130 8th-C74_S129 8th-C75_S128 8th-C79_S140 8th-C7_S95 8th-C84_S143
#> "021" "01" "01" "021" "024" "01" "021"
#> 8th-C85_S150 8th-C87_S148 8th-C90_S152 8th-C91_S158 8th-C92_S157 8th-C94_S162 8th-C95_S161
#> "01" "01" "024" "022" "01" "024" "01"
#> 9th-C10_S18 9th-C11_S17 9th-C13_S24 9th-C14_S23 9th-C15_S22 9th-C16_S30 9th-C17_S29
#> "01" "01" "021" "021" "01" "01" "01"
#> 9th-C19_S36 9th-C1_S3 9th-C20_S35 9th-C22_S41 9th-C25_S45 9th-C28_S50 9th-C29_S51
#> "01" "01" "022" "023" "021" "01" "01"
#> 9th-C2_S2 9th-C30_S52 9th-C36_S59 9th-C38_S64 9th-C3_S1 9th-C40_S69 9th-C41_S70
#> "023" "01" "01" "01" "01" "01" "01"
#> 9th-C46_S79 9th-C49_S4 9th-C51_S6 9th-C52_S10 9th-C57_S16 9th-C59_S20 9th-C5_S8
#> "01" "024" "021" "024" "01" "021" "01"
#> 9th-C61_S25 9th-C62_S26 9th-C64_S31 9th-C65_S32 9th-C66_S33 9th-C67_S37 9th-C69_S39
#> "01" "01" "01" "01" "01" "01" "021"
#> 9th-C6_S7 9th-C70_S42 9th-C74_S48 9th-C75_S47 9th-C77_S53 9th-C79_S57 9th-C80_S56
#> "01" "01" "01" "024" "01" "024" "01"
#> 9th-C81_S55 9th-C83_S61 9th-C84_S60 9th-C85_S68 9th-C86_S67 9th-C87_S66 9th-C88_S73
#> "01" "01" "01" "022" "01" "022" "021"
#> 9th-C89_S72 9th-C8_S14 9th-C91_S78 9th-C92_S77 9th-C93_S76 9th-C94_S83 9th-C96_S81
#> "01" "01" "021" "024" "01" "021" "01"
#> 9th-C9_S13
#> "01"
get_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 2868))
#> 10th_C10_S104 10th_C11_S96 10th_C13_S61 10th_C14_S53 10th_C16_S105 10th_C17_S97 10th_C19_S62
#> "01" "021" "01" "01" "01" "021" "01"
#> 10th_C1_S59 10th_C20_S54 10th_C23_S98 10th_C24_S90 10th_C28_S91 10th_C30_S107 10th_C31_S48
#> "01" "01" "01" "01" "022" "01" "01"
#> 10th_C32_S56 10th_C33_S64 10th_C34_S92 10th_C37_S49 10th_C41_S101 10th_C42_S109 10th_C43_S50
#> "021" "021" "024" "021" "01" "023" "022"
#> 10th_C45_S66 10th_C46_S94 10th_C4_S103 10th_C50_S73 10th_C51_S80 10th_C52_S110 10th_C53_S118
#> "01" "01" "01" "024" "022" "024" "022"
#> 10th_C54_S124 10th_C56_S74 10th_C57_S81 10th_C58_S111 10th_C5_S95 10th_C61_S68 10th_C63_S82
#> "01" "01" "022" "022" "022" "021" "023"
#> 10th_C64_S112 10th_C66_S126 10th_C68_S75 10th_C6_S88 10th_C73_S84 10th_C74_S76 10th_C76_S128
#> "021" "021" "01" "022" "01" "01" "01"
#> 10th_C77_S120 10th_C78_S114 10th_C7_S60 10th_C80_S77 10th_C81_S70 10th_C84_S115 10th_C85_S86
#> "023" "022" "01" "023" "01" "01" "01"
#> 10th_C86_S78 10th_C87_S71 10th_C88_S130 10th_C8_S52 10th_C90_S116 10th_C95_S123 10th_C96_S117
#> "023" "023" "01" "01" "01" "024" "01"
#> 11th-C10_S63 11th-C12_S47 11th-C16_S64 11th-C21_S4 11th-C22_S65 11th-C24_S49 11th-C26_S12
#> "022" "024" "01" "021" "021" "01" "023"
#> 11th-C27_S19 11th-C2_S8 11th-C30_S66 11th-C33_S20 11th-C36_S67 11th-C37_S6 11th-C39_S21
#> "021" "023" "022" "01" "01" "022" "01"
#> 11th-C40_S52 11th-C41_S60 11th-C43_S7 11th-C44_S15 11th-C49_S23 11th-C4_S62 11th-C51_S39
#> "01" "01" "023" "01" "01" "023" "01"
#> 11th-C53_S78 11th-C54_S86 11th-C55_S24 11th-C56_S32 11th-C57_S40 11th-C58_S71 11th-C5_S54
#> "01" "021" "023" "023" "024" "01" "01"
#> 11th-C61_S25 11th-C62_S33 11th-C64_S72 11th-C66_S88 11th-C67_S26 11th-C68_S34 11th-C77_S82
#> "01" "022" "023" "01" "022" "01" "023"
#> 11th-C7_S16 11th-C93_S30 12th-C10_S155 12th-C11_S147 12th-C12_S139 12th-C14_S190 12th-C15_S183
#> "01" "022" "021" "01" "01" "01" "021"
#> 12th-C1_S195 12th-C20_S191 12th-C21_S184 12th-C23_S149 12th-C24_S141 12th-C25_S185 12th-C26_S192
#> "022" "01" "021" "022" "01" "01" "01"
#> 12th-C28_S142 12th-C29_S150 12th-C30_S157 12th-C33_S200 12th-C35_S151 12th-C36_S158 12th-C37_S187
#> "01" "01" "01" "01" "021" "023" "022"
#> 12th-C38_S194 12th-C39_S201 12th-C3_S181 12th-C40_S144 12th-C42_S159 12th-C46_S145 12th-C47_S153
#> "021" "022" "021" "022" "01" "01" "021"
#> 12th-C48_S160 12th-C4_S154 12th-C50_S210 12th-C51_S217 12th-C53_S168 12th-C55_S203 12th-C56_S211
#> "01" "022" "024" "01" "023" "01" "023"
#> 12th-C57_S218 12th-C58_S162 12th-C59_S169 12th-C60_S176 12th-C63_S219 12th-C64_S163 12th-C65_S170
#> "024" "01" "01" "01" "01" "01" "01"
#> 12th-C67_S205 12th-C69_S135 12th-C71_S171 12th-C74_S214 12th-C75_S206 12th-C76_S177 12th-C7_S196
#> "021" "01" "022" "01" "022" "01" "01"
#> 12th-C80_S215 12th-C81_S207 12th-C84_S165 12th-C85_S137 12th-C8_S189 12th-C90_S166 12th-C93_S209
#> "01" "01" "01" "01" "022" "01" "021"
#> 12th-C94_S180 12th-C95_S174 12th-C96_S167 13th_C12_S178 13th_C13_S149 13th_C15_S134 13th_C16_S193
#> "01" "01" "01" "01" "01" "021" "01"
#> 13th_C17_S186 13th_C18_S179 13th_C1_S147 13th_C20_S142 13th_C21_S135 13th_C23_S187 13th_C27_S151
#> "022" "022" "022" "022" "022" "01" "023"
#> 13th_C29_S188 13th_C31_S137 13th_C34_S181 13th_C36_S196 13th_C38_S145 13th_C39_S153 13th_C3_S132
#> "022" "022" "01" "023" "022" "01" "022"
#> 13th_C46_S183 13th_C49_S155 13th_C4_S191 13th_C51_S170 13th_C52_S198 13th_C53_S205 13th_C54_S212
#> "022" "023" "022" "022" "022" "022" "022"
#> 13th_C55_S156 13th_C57_S171 13th_C5_S184 13th_C60_S213 13th_C63_S172 13th_C66_S214 13th_C68_S165
#> "022" "021" "022" "01" "022" "01" "022"
#> 13th_C69_S173 13th_C6_S177 13th_C70_S201 13th_C71_S208 13th_C72_S215 13th_C75_S159 13th_C76_S216
#> "022" "022" "022" "022" "023" "021" "01"
#> 13th_C77_S209 13th_C79_S174 13th_C80_S167 13th_C81_S160 13th_C86_S168 13th_C88_S218 13th_C89_S211
#> "022" "022" "021" "021" "022" "022" "022"
#> 13th_C8_S140 13th_C92_S169 13th_C93_S162 13th_C94_S219 13th_C96_S204 1st-61_S27 1st-C11_S58
#> "023" "022" "022" "01" "01" "01" "01"
#> 1st-C13_S19 1st-C15_S3 1st-C18_S51 1st-C19_S20 1st-C20_S12 1st-C21_S4 1st-C32_S14
#> "021" "022" "024" "01" "024" "01" "01"
#> 1st-C34_S54 1st-C39_S23 1st-C42_S71 1st-C50_S33 1st-C51_S41 1st-C53_S74 1st-C56_S34
#> "01" "021" "01" "01" "024" "024" "01"
#> 1st-C57_S42 1st-C58_S76 1st-C59_S77 1st-C62_S35 1st-C64_S79 1st-C68_S36 1st-C69_S44
#> "01" "01" "024" "024" "01" "01" "01"
#> 1st-C71_S83 1st-C73_S45 1st-C74_S37 1st-C75_S29 1st-C77_S86 1st-C78_S85 1st-C79_S46
#> "01" "01" "024" "01" "01" "01" "021"
#> 1st-C80_S38 1st-C8_S10 1st-C90_S91 1st-C96_S94 2nd-C11_S20 2nd-C15_S25 2nd-C16_S33
#> "01" "024" "01" "021" "01" "01" "01"
#> 2nd-C17_S32 2nd-C19_S39 2nd-C1_S3 2nd-C21_S37 2nd-C25_S49 2nd-C26_S50 2nd-C27_S51
#> "01" "021" "022" "01" "01" "01" "021"
#> 2nd-C28_S55 2nd-C29_S56 2nd-C2_S2 2nd-C31_S61 2nd-C32_S62 2nd-C36_S69 2nd-C37_S73
#> "024" "01" "023" "01" "01" "024" "021"
#> 2nd-C38_S74 2nd-C39_S75 2nd-C3_S1 2nd-C47_S92 2nd-C49_S4 2nd-C4_S9 2nd-C51_S6
#> "01" "01" "024" "01" "021" "024" "021"
#> 2nd-C52_S10 2nd-C54_S12 2nd-C57_S18 2nd-C58_S22 2nd-C5_S8 2nd-C62_S29 2nd-C67_S40
#> "021" "01" "01" "024" "021" "01" "01"
#> 2nd-C69_S42 2nd-C6_S7 2nd-C72_S48 2nd-C74_S53 2nd-C75_S52 2nd-C76_S60 2nd-C77_S59
#> "022" "01" "01" "01" "01" "01" "01"
#> 2nd-C7_S15 2nd-C80_S65 2nd-C81_S64 2nd-C83_S71 2nd-C86_S77 2nd-C87_S76 2nd-C88_S84
#> "021" "01" "01" "01" "01" "021" "01"
#> 2nd-C8_S14 2nd-C93_S88 2nd-C94_S96 2nd-C95_S95 3rd-C11_S58 3rd-C12_S68 3rd-C18_S80
#> "01" "01" "022" "01" "01" "01" "01"
#> 3rd-C1_S39 3rd-C20_S22 3rd-C21_S11 3rd-C23_S94 3rd-C25_S15 3rd-C26_S28 3rd-C27_S49
#> "01" "01" "01" "024" "021" "01" "01"
#> 3rd-C32_S31 3rd-C33_S50 3rd-C35_S23 3rd-C36_S2 3rd-C3_S2 3rd-C40_S57 3rd-C42_S74
#> "024" "01" "01" "01" "024" "01" "01"
#> 3rd-C44_S32 3rd-C46_S93 3rd-C47_S35 3rd-C49_S60 3rd-C4_S25 3rd-C51_S87 3rd-C52_S86
#> "024" "01" "01" "01" "01" "023" "024"
#> 3rd-C53_S67 3rd-C56_S90 3rd-C57_S5 3rd-C58_S3 3rd-C59_S91 3rd-C60_S10 3rd-C61_S64
#> "01" "021" "01" "01" "01" "021" "024"
#> 3rd-C63_S54 3rd-C65_S20 3rd-C67_S69 3rd-C68_S13 3rd-C69_S78 3rd-C6_S44 3rd-C71_S80
#> "024" "01" "01" "01" "024" "01" "01"
#> 3rd-C76_S22 3rd-C79_S67 3rd-C7_S40 3rd-C82_S11 3rd-C84_S75 3rd-C85_S79 3rd-C85_S83
#> "01" "01" "024" "01" "01" "01" "024"
#> 3rd-C86_S85 3rd-C87_S88 3rd-C88_S24 3rd-C91_S91 3rd-C92_S86 3rd-C95_S81 3rd-C96_S79
#> "01" "01" "01" "01" "01" "01" "021"
#> 3rd-C9_S5 4th-61_S28 4th-C12_S19 4th-C14_S26 4th-C18_S31 4th-C22_S45 4th-C23_S44
#> "01" "01" "01" "01" "01" "024" "01"
#> 4th-C24_S43 4th-C26_S50 4th-C27_S51 4th-C28_S55 4th-C29_S56 4th-C32_S62 4th-C33_S63
#> "01" "01" "023" "01" "01" "01" "01"
#> 4th-C35_S68 4th-C36_S69 4th-C37_S73 4th-C3_S1 4th-C40_S79 4th-C43_S85 4th-C45_S87
#> "024" "01" "024" "024" "01" "01" "021"
#> 4th-C49_S4 4th-C4_S9 4th-C50_S5 4th-C51_S6 4th-C56_S17 4th-C57_S18 4th-C59_S23
#> "01" "01" "024" "01" "01" "024" "01"
#> 4th-C5_S8 4th-C62_S29 4th-C63_S30 4th-C64_S34 4th-C66_S36 4th-C67_S40 4th-C68_S41
#> "01" "01" "01" "01" "01" "01" "022"
#> 4th-C69_S42 4th-C70_S46 4th-C73_S54 4th-C75_S52 4th-C78_S58 4th-C79_S66 4th-C7_S15
#> "01" "01" "01" "01" "01" "01" "01"
#> 4th-C80_S65 4th-C81_S64 4th-C82_S72 4th-C83_S71 4th-C85_S78 4th-C86_S77 4th-C87_S76
#> "01" "01" "01" "01" "01" "01" "01"
#> 4th-C88_S84 4th-C89_S83 4th-C8_S14 4th-C92_S89 4th-C93_S88 4th-C94_S96 4th-C95_S95
#> "01" "01" "01" "01" "021" "01" "01"
#> 4th-C96_S94 4th-C9_S13 5th-C10_S92 5th-C11_S91 5th-C12_S90 5th-C14_S97 5th-C16_S98
#> "01" "024" "023" "023" "01" "021" "023"
#> 5th-C18_S96 5th-C19_S104 5th-C21_S102 5th-C25_S108 5th-C30_S105 5th-C34_S108 5th-C35_S109
#> "021" "01" "01" "023" "01" "01" "01"
#> 5th-C40_S112 5th-C41_S113 5th-C42_S114 5th-C43_S121 5th-C45_S123 5th-C47_S118 5th-C49_S89
#> "023" "022" "023" "023" "023" "01" "01"
#> 5th-C50_S90 5th-C54_S89 5th-C56_S95 5th-C57_S96 5th-C58_S93 5th-C59_S94 5th-C5_S85
#> "01" "01" "023" "01" "023" "01" "01"
#> 5th-C64_S99 5th-C66_S101 5th-C67_S105 5th-C68_S106 5th-C69_S107 5th-C6_S84 5th-C70_S103
#> "01" "01" "023" "01" "01" "024" "024"
#> 5th-C73_S111 5th-C74_S110 5th-C77_S107 5th-C7_S93 5th-C80_S116 5th-C81_S115 5th-C83_S111
#> "023" "01" "01" "01" "021" "023" "022"
#> 5th-C87_S119 5th-C88_S117 5th-C90_S115 5th-C92_S124 5th-C9_S92 6th-C12_S18 6th-C15_S22
#> "024" "023" "01" "01" "01" "01" "021"
#> 6th-C16_S29 6th-C19_S35 6th-C1_S3 6th-C20_S34 6th-C21_S33 6th-C22_S39 6th-C23_S38
#> "01" "021" "021" "01" "01" "01" "01"
#> 6th-C24_S37 6th-C25_S43 6th-C28_S49 6th-C29_S50 6th-C2_S2 6th-C30_S51 6th-C34_S61
#> "01" "021" "021" "01" "01" "01" "022"
#> 6th-C40_S73 6th-C42_S75 6th-C45_S81 6th-C51_S6 6th-C53_S10 6th-C54_S11 6th-C57_S17
#> "01" "01" "022" "01" "01" "01" "021"
#> 6th-C58_S20 6th-C59_S21 6th-C5_S8 6th-C62_S25 6th-C63_S26 6th-C64_S30 6th-C65_S31
#> "021" "01" "01" "021" "01" "021" "01"
#> 6th-C66_S32 6th-C67_S36 6th-C71_S41 6th-C73_S48 6th-C75_S46 6th-C77_S53 6th-C79_S60
#> "01" "021" "01" "01" "01" "01" "01"
#> 6th-C80_S59 6th-C82_S66 6th-C83_S65 6th-C84_S64 6th-C85_S72 6th-C87_S70 6th-C89_S77
#> "01" "021" "024" "021" "01" "01" "021"
#> 6th-C90_S76 6th-C91_S84 6th-C93_S82 6th-C9_S12 7th-C10_S19 7th-C11_S18 7th-C12_S17
#> "021" "01" "01" "022" "01" "01" "021"
#> 7th-C14_S24 7th-C15_S23 7th-C17_S29 7th-C19_S36 7th-C1_S3 7th-C20_S35 7th-C21_S34
#> "01" "01" "01" "021" "021" "021" "021"
#> 7th-C24_S40 7th-C25_S43 7th-C28_S48 7th-C2_S2 7th-C31_S53 7th-C32_S54 7th-C34_S59
#> "01" "01" "021" "021" "01" "01" "01"
#> 7th-C36_S61 7th-C3_S1 7th-C40_S70 7th-C44_S76 7th-C45_S77 7th-C47_S81 7th-C49_S4
#> "01" "021" "01" "01" "01" "022" "022"
#> 7th-C4_S8 7th-C50_S5 7th-C52_S9 7th-C53_S10 7th-C56_S15 7th-C57_S16 7th-C58_S20
#> "021" "01" "021" "01" "01" "021" "01"
#> 7th-C59_S21 7th-C60_S22 7th-C62_S27 7th-C64_S31 7th-C65_S32 7th-C66_S33 7th-C68_S38
#> "01" "021" "01" "01" "021" "01" "01"
#> 7th-C69_S39 7th-C72_S42 7th-C73_S47 7th-C76_S52 7th-C77_S51 7th-C79_S58 7th-C80_S57
#> "01" "01" "01" "023" "01" "01" "01"
#> 7th-C81_S56 7th-C82_S64 7th-C84_S62 7th-C85_S69 7th-C88_S75 7th-C89_S74 7th-C8_S13
#> "023" "01" "01" "022" "01" "01" "01"
#> 7th-C90_S73 7th-C94_S83 7th-C96_S82 8th-C10_S100 8th-C11_S99 8th-C18_S110 8th-C20_S116
#> "01" "021" "01" "01" "01" "022" "01"
#> 8th-C21_S115 8th-C23_S121 8th-C24_S120 8th-C26_S126 8th-C28_S131 8th-C2_S85 8th-C34_S141
#> "022" "024" "01" "022" "024" "01" "01"
#> 8th-C37_S146 8th-C38_S147 8th-C44_S155 8th-C47_S160 8th-C55_S96 8th-C57_S98 8th-C58_S101
#> "022" "021" "01" "021" "01" "01" "01"
#> 8th-C59_S102 8th-C61_S107 8th-C64_S112 8th-C65_S113 8th-C67_S117 8th-C69_S119 8th-C6_S88
#> "01" "01" "01" "01" "01" "022" "01"
#> 8th-C70_S123 8th-C73_S130 8th-C74_S129 8th-C75_S128 8th-C79_S140 8th-C7_S95 8th-C84_S143
#> "021" "01" "01" "021" "024" "01" "021"
#> 8th-C85_S150 8th-C87_S148 8th-C90_S152 8th-C91_S158 8th-C92_S157 8th-C94_S162 8th-C95_S161
#> "01" "01" "024" "022" "01" "024" "01"
#> 9th-C10_S18 9th-C11_S17 9th-C13_S24 9th-C14_S23 9th-C15_S22 9th-C16_S30 9th-C17_S29
#> "01" "01" "021" "021" "01" "01" "01"
#> 9th-C19_S36 9th-C1_S3 9th-C20_S35 9th-C22_S41 9th-C25_S45 9th-C28_S50 9th-C29_S51
#> "01" "01" "022" "023" "021" "01" "01"
#> 9th-C2_S2 9th-C30_S52 9th-C36_S59 9th-C38_S64 9th-C3_S1 9th-C40_S69 9th-C41_S70
#> "023" "01" "01" "01" "01" "01" "01"
#> 9th-C46_S79 9th-C49_S4 9th-C51_S6 9th-C52_S10 9th-C57_S16 9th-C59_S20 9th-C5_S8
#> "01" "024" "021" "024" "01" "021" "01"
#> 9th-C61_S25 9th-C62_S26 9th-C64_S31 9th-C65_S32 9th-C66_S33 9th-C67_S37 9th-C69_S39
#> "01" "01" "01" "01" "01" "01" "021"
#> 9th-C6_S7 9th-C70_S42 9th-C74_S48 9th-C75_S47 9th-C77_S53 9th-C79_S57 9th-C80_S56
#> "01" "01" "01" "024" "01" "024" "01"
#> 9th-C81_S55 9th-C83_S61 9th-C84_S60 9th-C85_S68 9th-C86_S67 9th-C87_S66 9th-C88_S73
#> "01" "01" "01" "022" "01" "022" "021"
#> 9th-C89_S72 9th-C8_S14 9th-C91_S78 9th-C92_S77 9th-C93_S76 9th-C94_S83 9th-C96_S81
#> "01" "01" "021" "024" "01" "021" "01"
#> 9th-C9_S13
#> "01"
get_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 4252))
#> 10th_C10_S104 10th_C11_S96 10th_C13_S61 10th_C14_S53 10th_C16_S105 10th_C17_S97 10th_C19_S62
#> NA NA NA NA NA NA NA
#> 10th_C1_S59 10th_C20_S54 10th_C23_S98 10th_C24_S90 10th_C28_S91 10th_C30_S107 10th_C31_S48
#> NA NA NA NA NA NA NA
#> 10th_C32_S56 10th_C33_S64 10th_C34_S92 10th_C37_S49 10th_C41_S101 10th_C42_S109 10th_C43_S50
#> NA NA NA NA NA NA NA
#> 10th_C45_S66 10th_C46_S94 10th_C4_S103 10th_C50_S73 10th_C51_S80 10th_C52_S110 10th_C53_S118
#> NA NA NA NA NA NA NA
#> 10th_C54_S124 10th_C56_S74 10th_C57_S81 10th_C58_S111 10th_C5_S95 10th_C61_S68 10th_C63_S82
#> NA NA NA NA NA NA NA
#> 10th_C64_S112 10th_C66_S126 10th_C68_S75 10th_C6_S88 10th_C73_S84 10th_C74_S76 10th_C76_S128
#> NA NA NA NA NA NA NA
#> 10th_C77_S120 10th_C78_S114 10th_C7_S60 10th_C80_S77 10th_C81_S70 10th_C84_S115 10th_C85_S86
#> NA NA NA NA NA NA NA
#> 10th_C86_S78 10th_C87_S71 10th_C88_S130 10th_C8_S52 10th_C90_S116 10th_C95_S123 10th_C96_S117
#> NA NA NA NA NA NA NA
#> 11th-C10_S63 11th-C12_S47 11th-C16_S64 11th-C21_S4 11th-C22_S65 11th-C24_S49 11th-C26_S12
#> NA NA NA NA NA NA NA
#> 11th-C27_S19 11th-C2_S8 11th-C30_S66 11th-C33_S20 11th-C36_S67 11th-C37_S6 11th-C39_S21
#> NA NA NA NA NA NA NA
#> 11th-C40_S52 11th-C41_S60 11th-C43_S7 11th-C44_S15 11th-C49_S23 11th-C4_S62 11th-C51_S39
#> NA NA NA NA NA NA NA
#> 11th-C53_S78 11th-C54_S86 11th-C55_S24 11th-C56_S32 11th-C57_S40 11th-C58_S71 11th-C5_S54
#> NA NA NA NA NA NA NA
#> 11th-C61_S25 11th-C62_S33 11th-C64_S72 11th-C66_S88 11th-C67_S26 11th-C68_S34 11th-C77_S82
#> NA NA NA NA NA NA NA
#> 11th-C7_S16 11th-C93_S30 12th-C10_S155 12th-C11_S147 12th-C12_S139 12th-C14_S190 12th-C15_S183
#> NA NA NA NA NA NA NA
#> 12th-C1_S195 12th-C20_S191 12th-C21_S184 12th-C23_S149 12th-C24_S141 12th-C25_S185 12th-C26_S192
#> NA NA NA NA NA NA NA
#> 12th-C28_S142 12th-C29_S150 12th-C30_S157 12th-C33_S200 12th-C35_S151 12th-C36_S158 12th-C37_S187
#> NA NA NA NA NA NA NA
#> 12th-C38_S194 12th-C39_S201 12th-C3_S181 12th-C40_S144 12th-C42_S159 12th-C46_S145 12th-C47_S153
#> NA NA NA NA NA NA NA
#> 12th-C48_S160 12th-C4_S154 12th-C50_S210 12th-C51_S217 12th-C53_S168 12th-C55_S203 12th-C56_S211
#> NA NA NA NA NA NA NA
#> 12th-C57_S218 12th-C58_S162 12th-C59_S169 12th-C60_S176 12th-C63_S219 12th-C64_S163 12th-C65_S170
#> NA NA NA NA NA NA NA
#> 12th-C67_S205 12th-C69_S135 12th-C71_S171 12th-C74_S214 12th-C75_S206 12th-C76_S177 12th-C7_S196
#> NA NA NA NA NA NA NA
#> 12th-C80_S215 12th-C81_S207 12th-C84_S165 12th-C85_S137 12th-C8_S189 12th-C90_S166 12th-C93_S209
#> NA NA NA NA NA NA NA
#> 12th-C94_S180 12th-C95_S174 12th-C96_S167 13th_C12_S178 13th_C13_S149 13th_C15_S134 13th_C16_S193
#> NA NA NA NA NA NA NA
#> 13th_C17_S186 13th_C18_S179 13th_C1_S147 13th_C20_S142 13th_C21_S135 13th_C23_S187 13th_C27_S151
#> NA NA NA NA NA NA NA
#> 13th_C29_S188 13th_C31_S137 13th_C34_S181 13th_C36_S196 13th_C38_S145 13th_C39_S153 13th_C3_S132
#> NA NA NA NA NA NA NA
#> 13th_C46_S183 13th_C49_S155 13th_C4_S191 13th_C51_S170 13th_C52_S198 13th_C53_S205 13th_C54_S212
#> NA NA NA NA NA NA NA
#> 13th_C55_S156 13th_C57_S171 13th_C5_S184 13th_C60_S213 13th_C63_S172 13th_C66_S214 13th_C68_S165
#> NA NA NA NA NA NA NA
#> 13th_C69_S173 13th_C6_S177 13th_C70_S201 13th_C71_S208 13th_C72_S215 13th_C75_S159 13th_C76_S216
#> NA NA NA NA NA NA NA
#> 13th_C77_S209 13th_C79_S174 13th_C80_S167 13th_C81_S160 13th_C86_S168 13th_C88_S218 13th_C89_S211
#> NA NA NA NA NA NA NA
#> 13th_C8_S140 13th_C92_S169 13th_C93_S162 13th_C94_S219 13th_C96_S204 1st-61_S27 1st-C11_S58
#> NA NA NA NA NA NA NA
#> 1st-C13_S19 1st-C15_S3 1st-C18_S51 1st-C19_S20 1st-C20_S12 1st-C21_S4 1st-C32_S14
#> NA NA NA NA NA NA NA
#> 1st-C34_S54 1st-C39_S23 1st-C42_S71 1st-C50_S33 1st-C51_S41 1st-C53_S74 1st-C56_S34
#> NA NA NA NA NA NA NA
#> 1st-C57_S42 1st-C58_S76 1st-C59_S77 1st-C62_S35 1st-C64_S79 1st-C68_S36 1st-C69_S44
#> NA NA NA NA NA NA NA
#> 1st-C71_S83 1st-C73_S45 1st-C74_S37 1st-C75_S29 1st-C77_S86 1st-C78_S85 1st-C79_S46
#> NA NA NA NA NA NA NA
#> 1st-C80_S38 1st-C8_S10 1st-C90_S91 1st-C96_S94 2nd-C11_S20 2nd-C15_S25 2nd-C16_S33
#> NA NA NA NA NA NA NA
#> 2nd-C17_S32 2nd-C19_S39 2nd-C1_S3 2nd-C21_S37 2nd-C25_S49 2nd-C26_S50 2nd-C27_S51
#> NA NA NA NA NA NA NA
#> 2nd-C28_S55 2nd-C29_S56 2nd-C2_S2 2nd-C31_S61 2nd-C32_S62 2nd-C36_S69 2nd-C37_S73
#> NA NA NA NA NA NA NA
#> 2nd-C38_S74 2nd-C39_S75 2nd-C3_S1 2nd-C47_S92 2nd-C49_S4 2nd-C4_S9 2nd-C51_S6
#> NA NA NA NA NA NA NA
#> 2nd-C52_S10 2nd-C54_S12 2nd-C57_S18 2nd-C58_S22 2nd-C5_S8 2nd-C62_S29 2nd-C67_S40
#> NA NA NA NA NA NA NA
#> 2nd-C69_S42 2nd-C6_S7 2nd-C72_S48 2nd-C74_S53 2nd-C75_S52 2nd-C76_S60 2nd-C77_S59
#> NA NA NA NA NA NA NA
#> 2nd-C7_S15 2nd-C80_S65 2nd-C81_S64 2nd-C83_S71 2nd-C86_S77 2nd-C87_S76 2nd-C88_S84
#> NA NA NA NA NA NA NA
#> 2nd-C8_S14 2nd-C93_S88 2nd-C94_S96 2nd-C95_S95 3rd-C11_S58 3rd-C12_S68 3rd-C18_S80
#> NA NA NA NA NA NA NA
#> 3rd-C1_S39 3rd-C20_S22 3rd-C21_S11 3rd-C23_S94 3rd-C25_S15 3rd-C26_S28 3rd-C27_S49
#> NA NA NA NA NA NA NA
#> 3rd-C32_S31 3rd-C33_S50 3rd-C35_S23 3rd-C36_S2 3rd-C3_S2 3rd-C40_S57 3rd-C42_S74
#> NA NA NA NA NA NA NA
#> 3rd-C44_S32 3rd-C46_S93 3rd-C47_S35 3rd-C49_S60 3rd-C4_S25 3rd-C51_S87 3rd-C52_S86
#> NA NA NA NA NA NA NA
#> 3rd-C53_S67 3rd-C56_S90 3rd-C57_S5 3rd-C58_S3 3rd-C59_S91 3rd-C60_S10 3rd-C61_S64
#> NA NA NA NA NA NA NA
#> 3rd-C63_S54 3rd-C65_S20 3rd-C67_S69 3rd-C68_S13 3rd-C69_S78 3rd-C6_S44 3rd-C71_S80
#> NA NA NA NA NA NA NA
#> 3rd-C76_S22 3rd-C79_S67 3rd-C7_S40 3rd-C82_S11 3rd-C84_S75 3rd-C85_S79 3rd-C85_S83
#> NA NA NA NA NA NA NA
#> 3rd-C86_S85 3rd-C87_S88 3rd-C88_S24 3rd-C91_S91 3rd-C92_S86 3rd-C95_S81 3rd-C96_S79
#> NA NA NA NA NA NA NA
#> 3rd-C9_S5 4th-61_S28 4th-C12_S19 4th-C14_S26 4th-C18_S31 4th-C22_S45 4th-C23_S44
#> NA NA NA NA NA NA NA
#> 4th-C24_S43 4th-C26_S50 4th-C27_S51 4th-C28_S55 4th-C29_S56 4th-C32_S62 4th-C33_S63
#> NA NA NA NA NA NA NA
#> 4th-C35_S68 4th-C36_S69 4th-C37_S73 4th-C3_S1 4th-C40_S79 4th-C43_S85 4th-C45_S87
#> NA NA NA NA NA NA NA
#> 4th-C49_S4 4th-C4_S9 4th-C50_S5 4th-C51_S6 4th-C56_S17 4th-C57_S18 4th-C59_S23
#> NA NA NA NA NA NA NA
#> 4th-C5_S8 4th-C62_S29 4th-C63_S30 4th-C64_S34 4th-C66_S36 4th-C67_S40 4th-C68_S41
#> NA NA NA NA NA NA NA
#> 4th-C69_S42 4th-C70_S46 4th-C73_S54 4th-C75_S52 4th-C78_S58 4th-C79_S66 4th-C7_S15
#> NA NA NA NA NA NA NA
#> 4th-C80_S65 4th-C81_S64 4th-C82_S72 4th-C83_S71 4th-C85_S78 4th-C86_S77 4th-C87_S76
#> NA NA NA NA NA NA NA
#> 4th-C88_S84 4th-C89_S83 4th-C8_S14 4th-C92_S89 4th-C93_S88 4th-C94_S96 4th-C95_S95
#> NA NA NA NA NA NA NA
#> 4th-C96_S94 4th-C9_S13 5th-C10_S92 5th-C11_S91 5th-C12_S90 5th-C14_S97 5th-C16_S98
#> NA NA NA NA NA NA NA
#> 5th-C18_S96 5th-C19_S104 5th-C21_S102 5th-C25_S108 5th-C30_S105 5th-C34_S108 5th-C35_S109
#> NA NA NA NA NA NA NA
#> 5th-C40_S112 5th-C41_S113 5th-C42_S114 5th-C43_S121 5th-C45_S123 5th-C47_S118 5th-C49_S89
#> NA NA NA NA NA NA NA
#> 5th-C50_S90 5th-C54_S89 5th-C56_S95 5th-C57_S96 5th-C58_S93 5th-C59_S94 5th-C5_S85
#> NA NA NA NA NA NA NA
#> 5th-C64_S99 5th-C66_S101 5th-C67_S105 5th-C68_S106 5th-C69_S107 5th-C6_S84 5th-C70_S103
#> NA NA NA NA NA NA NA
#> 5th-C73_S111 5th-C74_S110 5th-C77_S107 5th-C7_S93 5th-C80_S116 5th-C81_S115 5th-C83_S111
#> NA NA NA NA NA NA NA
#> 5th-C87_S119 5th-C88_S117 5th-C90_S115 5th-C92_S124 5th-C9_S92 6th-C12_S18 6th-C15_S22
#> NA NA NA NA NA NA NA
#> 6th-C16_S29 6th-C19_S35 6th-C1_S3 6th-C20_S34 6th-C21_S33 6th-C22_S39 6th-C23_S38
#> NA NA NA NA NA NA NA
#> 6th-C24_S37 6th-C25_S43 6th-C28_S49 6th-C29_S50 6th-C2_S2 6th-C30_S51 6th-C34_S61
#> NA NA NA NA NA NA NA
#> 6th-C40_S73 6th-C42_S75 6th-C45_S81 6th-C51_S6 6th-C53_S10 6th-C54_S11 6th-C57_S17
#> NA NA NA NA NA NA NA
#> 6th-C58_S20 6th-C59_S21 6th-C5_S8 6th-C62_S25 6th-C63_S26 6th-C64_S30 6th-C65_S31
#> NA NA NA NA NA NA NA
#> 6th-C66_S32 6th-C67_S36 6th-C71_S41 6th-C73_S48 6th-C75_S46 6th-C77_S53 6th-C79_S60
#> NA NA NA NA NA NA NA
#> 6th-C80_S59 6th-C82_S66 6th-C83_S65 6th-C84_S64 6th-C85_S72 6th-C87_S70 6th-C89_S77
#> NA NA NA NA NA NA NA
#> 6th-C90_S76 6th-C91_S84 6th-C93_S82 6th-C9_S12 7th-C10_S19 7th-C11_S18 7th-C12_S17
#> NA NA NA NA NA NA NA
#> 7th-C14_S24 7th-C15_S23 7th-C17_S29 7th-C19_S36 7th-C1_S3 7th-C20_S35 7th-C21_S34
#> NA NA NA NA NA NA NA
#> 7th-C24_S40 7th-C25_S43 7th-C28_S48 7th-C2_S2 7th-C31_S53 7th-C32_S54 7th-C34_S59
#> NA NA NA NA NA NA NA
#> 7th-C36_S61 7th-C3_S1 7th-C40_S70 7th-C44_S76 7th-C45_S77 7th-C47_S81 7th-C49_S4
#> NA NA NA NA NA NA NA
#> 7th-C4_S8 7th-C50_S5 7th-C52_S9 7th-C53_S10 7th-C56_S15 7th-C57_S16 7th-C58_S20
#> NA NA NA NA NA NA NA
#> 7th-C59_S21 7th-C60_S22 7th-C62_S27 7th-C64_S31 7th-C65_S32 7th-C66_S33 7th-C68_S38
#> NA NA NA NA NA NA NA
#> 7th-C69_S39 7th-C72_S42 7th-C73_S47 7th-C76_S52 7th-C77_S51 7th-C79_S58 7th-C80_S57
#> NA NA NA NA NA NA NA
#> 7th-C81_S56 7th-C82_S64 7th-C84_S62 7th-C85_S69 7th-C88_S75 7th-C89_S74 7th-C8_S13
#> NA NA NA NA NA NA NA
#> 7th-C90_S73 7th-C94_S83 7th-C96_S82 8th-C10_S100 8th-C11_S99 8th-C18_S110 8th-C20_S116
#> NA NA NA NA NA NA NA
#> 8th-C21_S115 8th-C23_S121 8th-C24_S120 8th-C26_S126 8th-C28_S131 8th-C2_S85 8th-C34_S141
#> NA NA NA NA NA NA NA
#> 8th-C37_S146 8th-C38_S147 8th-C44_S155 8th-C47_S160 8th-C55_S96 8th-C57_S98 8th-C58_S101
#> NA NA NA NA NA NA NA
#> 8th-C59_S102 8th-C61_S107 8th-C64_S112 8th-C65_S113 8th-C67_S117 8th-C69_S119 8th-C6_S88
#> NA NA NA NA NA NA NA
#> 8th-C70_S123 8th-C73_S130 8th-C74_S129 8th-C75_S128 8th-C79_S140 8th-C7_S95 8th-C84_S143
#> NA NA NA NA NA NA NA
#> 8th-C85_S150 8th-C87_S148 8th-C90_S152 8th-C91_S158 8th-C92_S157 8th-C94_S162 8th-C95_S161
#> NA NA NA NA NA NA NA
#> 9th-C10_S18 9th-C11_S17 9th-C13_S24 9th-C14_S23 9th-C15_S22 9th-C16_S30 9th-C17_S29
#> NA NA NA NA NA NA NA
#> 9th-C19_S36 9th-C1_S3 9th-C20_S35 9th-C22_S41 9th-C25_S45 9th-C28_S50 9th-C29_S51
#> NA NA NA NA NA NA NA
#> 9th-C2_S2 9th-C30_S52 9th-C36_S59 9th-C38_S64 9th-C3_S1 9th-C40_S69 9th-C41_S70
#> NA NA NA NA NA NA NA
#> 9th-C46_S79 9th-C49_S4 9th-C51_S6 9th-C52_S10 9th-C57_S16 9th-C59_S20 9th-C5_S8
#> NA NA NA NA NA NA NA
#> 9th-C61_S25 9th-C62_S26 9th-C64_S31 9th-C65_S32 9th-C66_S33 9th-C67_S37 9th-C69_S39
#> NA NA NA NA NA NA NA
#> 9th-C6_S7 9th-C70_S42 9th-C74_S48 9th-C75_S47 9th-C77_S53 9th-C79_S57 9th-C80_S56
#> NA NA NA NA NA NA NA
#> 9th-C81_S55 9th-C83_S61 9th-C84_S60 9th-C85_S68 9th-C86_S67 9th-C87_S66 9th-C88_S73
#> NA NA NA NA NA NA NA
#> 9th-C89_S72 9th-C8_S14 9th-C91_S78 9th-C92_S77 9th-C93_S76 9th-C94_S83 9th-C96_S81
#> NA NA NA NA NA NA NA
#> 9th-C9_S13
#> NA
get_classes(res_rh, merge_node = merge_node_param(min_n_signatures = 5379))
#> 10th_C10_S104 10th_C11_S96 10th_C13_S61 10th_C14_S53 10th_C16_S105 10th_C17_S97 10th_C19_S62
#> NA NA NA NA NA NA NA
#> 10th_C1_S59 10th_C20_S54 10th_C23_S98 10th_C24_S90 10th_C28_S91 10th_C30_S107 10th_C31_S48
#> NA NA NA NA NA NA NA
#> 10th_C32_S56 10th_C33_S64 10th_C34_S92 10th_C37_S49 10th_C41_S101 10th_C42_S109 10th_C43_S50
#> NA NA NA NA NA NA NA
#> 10th_C45_S66 10th_C46_S94 10th_C4_S103 10th_C50_S73 10th_C51_S80 10th_C52_S110 10th_C53_S118
#> NA NA NA NA NA NA NA
#> 10th_C54_S124 10th_C56_S74 10th_C57_S81 10th_C58_S111 10th_C5_S95 10th_C61_S68 10th_C63_S82
#> NA NA NA NA NA NA NA
#> 10th_C64_S112 10th_C66_S126 10th_C68_S75 10th_C6_S88 10th_C73_S84 10th_C74_S76 10th_C76_S128
#> NA NA NA NA NA NA NA
#> 10th_C77_S120 10th_C78_S114 10th_C7_S60 10th_C80_S77 10th_C81_S70 10th_C84_S115 10th_C85_S86
#> NA NA NA NA NA NA NA
#> 10th_C86_S78 10th_C87_S71 10th_C88_S130 10th_C8_S52 10th_C90_S116 10th_C95_S123 10th_C96_S117
#> NA NA NA NA NA NA NA
#> 11th-C10_S63 11th-C12_S47 11th-C16_S64 11th-C21_S4 11th-C22_S65 11th-C24_S49 11th-C26_S12
#> NA NA NA NA NA NA NA
#> 11th-C27_S19 11th-C2_S8 11th-C30_S66 11th-C33_S20 11th-C36_S67 11th-C37_S6 11th-C39_S21
#> NA NA NA NA NA NA NA
#> 11th-C40_S52 11th-C41_S60 11th-C43_S7 11th-C44_S15 11th-C49_S23 11th-C4_S62 11th-C51_S39
#> NA NA NA NA NA NA NA
#> 11th-C53_S78 11th-C54_S86 11th-C55_S24 11th-C56_S32 11th-C57_S40 11th-C58_S71 11th-C5_S54
#> NA NA NA NA NA NA NA
#> 11th-C61_S25 11th-C62_S33 11th-C64_S72 11th-C66_S88 11th-C67_S26 11th-C68_S34 11th-C77_S82
#> NA NA NA NA NA NA NA
#> 11th-C7_S16 11th-C93_S30 12th-C10_S155 12th-C11_S147 12th-C12_S139 12th-C14_S190 12th-C15_S183
#> NA NA NA NA NA NA NA
#> 12th-C1_S195 12th-C20_S191 12th-C21_S184 12th-C23_S149 12th-C24_S141 12th-C25_S185 12th-C26_S192
#> NA NA NA NA NA NA NA
#> 12th-C28_S142 12th-C29_S150 12th-C30_S157 12th-C33_S200 12th-C35_S151 12th-C36_S158 12th-C37_S187
#> NA NA NA NA NA NA NA
#> 12th-C38_S194 12th-C39_S201 12th-C3_S181 12th-C40_S144 12th-C42_S159 12th-C46_S145 12th-C47_S153
#> NA NA NA NA NA NA NA
#> 12th-C48_S160 12th-C4_S154 12th-C50_S210 12th-C51_S217 12th-C53_S168 12th-C55_S203 12th-C56_S211
#> NA NA NA NA NA NA NA
#> 12th-C57_S218 12th-C58_S162 12th-C59_S169 12th-C60_S176 12th-C63_S219 12th-C64_S163 12th-C65_S170
#> NA NA NA NA NA NA NA
#> 12th-C67_S205 12th-C69_S135 12th-C71_S171 12th-C74_S214 12th-C75_S206 12th-C76_S177 12th-C7_S196
#> NA NA NA NA NA NA NA
#> 12th-C80_S215 12th-C81_S207 12th-C84_S165 12th-C85_S137 12th-C8_S189 12th-C90_S166 12th-C93_S209
#> NA NA NA NA NA NA NA
#> 12th-C94_S180 12th-C95_S174 12th-C96_S167 13th_C12_S178 13th_C13_S149 13th_C15_S134 13th_C16_S193
#> NA NA NA NA NA NA NA
#> 13th_C17_S186 13th_C18_S179 13th_C1_S147 13th_C20_S142 13th_C21_S135 13th_C23_S187 13th_C27_S151
#> NA NA NA NA NA NA NA
#> 13th_C29_S188 13th_C31_S137 13th_C34_S181 13th_C36_S196 13th_C38_S145 13th_C39_S153 13th_C3_S132
#> NA NA NA NA NA NA NA
#> 13th_C46_S183 13th_C49_S155 13th_C4_S191 13th_C51_S170 13th_C52_S198 13th_C53_S205 13th_C54_S212
#> NA NA NA NA NA NA NA
#> 13th_C55_S156 13th_C57_S171 13th_C5_S184 13th_C60_S213 13th_C63_S172 13th_C66_S214 13th_C68_S165
#> NA NA NA NA NA NA NA
#> 13th_C69_S173 13th_C6_S177 13th_C70_S201 13th_C71_S208 13th_C72_S215 13th_C75_S159 13th_C76_S216
#> NA NA NA NA NA NA NA
#> 13th_C77_S209 13th_C79_S174 13th_C80_S167 13th_C81_S160 13th_C86_S168 13th_C88_S218 13th_C89_S211
#> NA NA NA NA NA NA NA
#> 13th_C8_S140 13th_C92_S169 13th_C93_S162 13th_C94_S219 13th_C96_S204 1st-61_S27 1st-C11_S58
#> NA NA NA NA NA NA NA
#> 1st-C13_S19 1st-C15_S3 1st-C18_S51 1st-C19_S20 1st-C20_S12 1st-C21_S4 1st-C32_S14
#> NA NA NA NA NA NA NA
#> 1st-C34_S54 1st-C39_S23 1st-C42_S71 1st-C50_S33 1st-C51_S41 1st-C53_S74 1st-C56_S34
#> NA NA NA NA NA NA NA
#> 1st-C57_S42 1st-C58_S76 1st-C59_S77 1st-C62_S35 1st-C64_S79 1st-C68_S36 1st-C69_S44
#> NA NA NA NA NA NA NA
#> 1st-C71_S83 1st-C73_S45 1st-C74_S37 1st-C75_S29 1st-C77_S86 1st-C78_S85 1st-C79_S46
#> NA NA NA NA NA NA NA
#> 1st-C80_S38 1st-C8_S10 1st-C90_S91 1st-C96_S94 2nd-C11_S20 2nd-C15_S25 2nd-C16_S33
#> NA NA NA NA NA NA NA
#> 2nd-C17_S32 2nd-C19_S39 2nd-C1_S3 2nd-C21_S37 2nd-C25_S49 2nd-C26_S50 2nd-C27_S51
#> NA NA NA NA NA NA NA
#> 2nd-C28_S55 2nd-C29_S56 2nd-C2_S2 2nd-C31_S61 2nd-C32_S62 2nd-C36_S69 2nd-C37_S73
#> NA NA NA NA NA NA NA
#> 2nd-C38_S74 2nd-C39_S75 2nd-C3_S1 2nd-C47_S92 2nd-C49_S4 2nd-C4_S9 2nd-C51_S6
#> NA NA NA NA NA NA NA
#> 2nd-C52_S10 2nd-C54_S12 2nd-C57_S18 2nd-C58_S22 2nd-C5_S8 2nd-C62_S29 2nd-C67_S40
#> NA NA NA NA NA NA NA
#> 2nd-C69_S42 2nd-C6_S7 2nd-C72_S48 2nd-C74_S53 2nd-C75_S52 2nd-C76_S60 2nd-C77_S59
#> NA NA NA NA NA NA NA
#> 2nd-C7_S15 2nd-C80_S65 2nd-C81_S64 2nd-C83_S71 2nd-C86_S77 2nd-C87_S76 2nd-C88_S84
#> NA NA NA NA NA NA NA
#> 2nd-C8_S14 2nd-C93_S88 2nd-C94_S96 2nd-C95_S95 3rd-C11_S58 3rd-C12_S68 3rd-C18_S80
#> NA NA NA NA NA NA NA
#> 3rd-C1_S39 3rd-C20_S22 3rd-C21_S11 3rd-C23_S94 3rd-C25_S15 3rd-C26_S28 3rd-C27_S49
#> NA NA NA NA NA NA NA
#> 3rd-C32_S31 3rd-C33_S50 3rd-C35_S23 3rd-C36_S2 3rd-C3_S2 3rd-C40_S57 3rd-C42_S74
#> NA NA NA NA NA NA NA
#> 3rd-C44_S32 3rd-C46_S93 3rd-C47_S35 3rd-C49_S60 3rd-C4_S25 3rd-C51_S87 3rd-C52_S86
#> NA NA NA NA NA NA NA
#> 3rd-C53_S67 3rd-C56_S90 3rd-C57_S5 3rd-C58_S3 3rd-C59_S91 3rd-C60_S10 3rd-C61_S64
#> NA NA NA NA NA NA NA
#> 3rd-C63_S54 3rd-C65_S20 3rd-C67_S69 3rd-C68_S13 3rd-C69_S78 3rd-C6_S44 3rd-C71_S80
#> NA NA NA NA NA NA NA
#> 3rd-C76_S22 3rd-C79_S67 3rd-C7_S40 3rd-C82_S11 3rd-C84_S75 3rd-C85_S79 3rd-C85_S83
#> NA NA NA NA NA NA NA
#> 3rd-C86_S85 3rd-C87_S88 3rd-C88_S24 3rd-C91_S91 3rd-C92_S86 3rd-C95_S81 3rd-C96_S79
#> NA NA NA NA NA NA NA
#> 3rd-C9_S5 4th-61_S28 4th-C12_S19 4th-C14_S26 4th-C18_S31 4th-C22_S45 4th-C23_S44
#> NA NA NA NA NA NA NA
#> 4th-C24_S43 4th-C26_S50 4th-C27_S51 4th-C28_S55 4th-C29_S56 4th-C32_S62 4th-C33_S63
#> NA NA NA NA NA NA NA
#> 4th-C35_S68 4th-C36_S69 4th-C37_S73 4th-C3_S1 4th-C40_S79 4th-C43_S85 4th-C45_S87
#> NA NA NA NA NA NA NA
#> 4th-C49_S4 4th-C4_S9 4th-C50_S5 4th-C51_S6 4th-C56_S17 4th-C57_S18 4th-C59_S23
#> NA NA NA NA NA NA NA
#> 4th-C5_S8 4th-C62_S29 4th-C63_S30 4th-C64_S34 4th-C66_S36 4th-C67_S40 4th-C68_S41
#> NA NA NA NA NA NA NA
#> 4th-C69_S42 4th-C70_S46 4th-C73_S54 4th-C75_S52 4th-C78_S58 4th-C79_S66 4th-C7_S15
#> NA NA NA NA NA NA NA
#> 4th-C80_S65 4th-C81_S64 4th-C82_S72 4th-C83_S71 4th-C85_S78 4th-C86_S77 4th-C87_S76
#> NA NA NA NA NA NA NA
#> 4th-C88_S84 4th-C89_S83 4th-C8_S14 4th-C92_S89 4th-C93_S88 4th-C94_S96 4th-C95_S95
#> NA NA NA NA NA NA NA
#> 4th-C96_S94 4th-C9_S13 5th-C10_S92 5th-C11_S91 5th-C12_S90 5th-C14_S97 5th-C16_S98
#> NA NA NA NA NA NA NA
#> 5th-C18_S96 5th-C19_S104 5th-C21_S102 5th-C25_S108 5th-C30_S105 5th-C34_S108 5th-C35_S109
#> NA NA NA NA NA NA NA
#> 5th-C40_S112 5th-C41_S113 5th-C42_S114 5th-C43_S121 5th-C45_S123 5th-C47_S118 5th-C49_S89
#> NA NA NA NA NA NA NA
#> 5th-C50_S90 5th-C54_S89 5th-C56_S95 5th-C57_S96 5th-C58_S93 5th-C59_S94 5th-C5_S85
#> NA NA NA NA NA NA NA
#> 5th-C64_S99 5th-C66_S101 5th-C67_S105 5th-C68_S106 5th-C69_S107 5th-C6_S84 5th-C70_S103
#> NA NA NA NA NA NA NA
#> 5th-C73_S111 5th-C74_S110 5th-C77_S107 5th-C7_S93 5th-C80_S116 5th-C81_S115 5th-C83_S111
#> NA NA NA NA NA NA NA
#> 5th-C87_S119 5th-C88_S117 5th-C90_S115 5th-C92_S124 5th-C9_S92 6th-C12_S18 6th-C15_S22
#> NA NA NA NA NA NA NA
#> 6th-C16_S29 6th-C19_S35 6th-C1_S3 6th-C20_S34 6th-C21_S33 6th-C22_S39 6th-C23_S38
#> NA NA NA NA NA NA NA
#> 6th-C24_S37 6th-C25_S43 6th-C28_S49 6th-C29_S50 6th-C2_S2 6th-C30_S51 6th-C34_S61
#> NA NA NA NA NA NA NA
#> 6th-C40_S73 6th-C42_S75 6th-C45_S81 6th-C51_S6 6th-C53_S10 6th-C54_S11 6th-C57_S17
#> NA NA NA NA NA NA NA
#> 6th-C58_S20 6th-C59_S21 6th-C5_S8 6th-C62_S25 6th-C63_S26 6th-C64_S30 6th-C65_S31
#> NA NA NA NA NA NA NA
#> 6th-C66_S32 6th-C67_S36 6th-C71_S41 6th-C73_S48 6th-C75_S46 6th-C77_S53 6th-C79_S60
#> NA NA NA NA NA NA NA
#> 6th-C80_S59 6th-C82_S66 6th-C83_S65 6th-C84_S64 6th-C85_S72 6th-C87_S70 6th-C89_S77
#> NA NA NA NA NA NA NA
#> 6th-C90_S76 6th-C91_S84 6th-C93_S82 6th-C9_S12 7th-C10_S19 7th-C11_S18 7th-C12_S17
#> NA NA NA NA NA NA NA
#> 7th-C14_S24 7th-C15_S23 7th-C17_S29 7th-C19_S36 7th-C1_S3 7th-C20_S35 7th-C21_S34
#> NA NA NA NA NA NA NA
#> 7th-C24_S40 7th-C25_S43 7th-C28_S48 7th-C2_S2 7th-C31_S53 7th-C32_S54 7th-C34_S59
#> NA NA NA NA NA NA NA
#> 7th-C36_S61 7th-C3_S1 7th-C40_S70 7th-C44_S76 7th-C45_S77 7th-C47_S81 7th-C49_S4
#> NA NA NA NA NA NA NA
#> 7th-C4_S8 7th-C50_S5 7th-C52_S9 7th-C53_S10 7th-C56_S15 7th-C57_S16 7th-C58_S20
#> NA NA NA NA NA NA NA
#> 7th-C59_S21 7th-C60_S22 7th-C62_S27 7th-C64_S31 7th-C65_S32 7th-C66_S33 7th-C68_S38
#> NA NA NA NA NA NA NA
#> 7th-C69_S39 7th-C72_S42 7th-C73_S47 7th-C76_S52 7th-C77_S51 7th-C79_S58 7th-C80_S57
#> NA NA NA NA NA NA NA
#> 7th-C81_S56 7th-C82_S64 7th-C84_S62 7th-C85_S69 7th-C88_S75 7th-C89_S74 7th-C8_S13
#> NA NA NA NA NA NA NA
#> 7th-C90_S73 7th-C94_S83 7th-C96_S82 8th-C10_S100 8th-C11_S99 8th-C18_S110 8th-C20_S116
#> NA NA NA NA NA NA NA
#> 8th-C21_S115 8th-C23_S121 8th-C24_S120 8th-C26_S126 8th-C28_S131 8th-C2_S85 8th-C34_S141
#> NA NA NA NA NA NA NA
#> 8th-C37_S146 8th-C38_S147 8th-C44_S155 8th-C47_S160 8th-C55_S96 8th-C57_S98 8th-C58_S101
#> NA NA NA NA NA NA NA
#> 8th-C59_S102 8th-C61_S107 8th-C64_S112 8th-C65_S113 8th-C67_S117 8th-C69_S119 8th-C6_S88
#> NA NA NA NA NA NA NA
#> 8th-C70_S123 8th-C73_S130 8th-C74_S129 8th-C75_S128 8th-C79_S140 8th-C7_S95 8th-C84_S143
#> NA NA NA NA NA NA NA
#> 8th-C85_S150 8th-C87_S148 8th-C90_S152 8th-C91_S158 8th-C92_S157 8th-C94_S162 8th-C95_S161
#> NA NA NA NA NA NA NA
#> 9th-C10_S18 9th-C11_S17 9th-C13_S24 9th-C14_S23 9th-C15_S22 9th-C16_S30 9th-C17_S29
#> NA NA NA NA NA NA NA
#> 9th-C19_S36 9th-C1_S3 9th-C20_S35 9th-C22_S41 9th-C25_S45 9th-C28_S50 9th-C29_S51
#> NA NA NA NA NA NA NA
#> 9th-C2_S2 9th-C30_S52 9th-C36_S59 9th-C38_S64 9th-C3_S1 9th-C40_S69 9th-C41_S70
#> NA NA NA NA NA NA NA
#> 9th-C46_S79 9th-C49_S4 9th-C51_S6 9th-C52_S10 9th-C57_S16 9th-C59_S20 9th-C5_S8
#> NA NA NA NA NA NA NA
#> 9th-C61_S25 9th-C62_S26 9th-C64_S31 9th-C65_S32 9th-C66_S33 9th-C67_S37 9th-C69_S39
#> NA NA NA NA NA NA NA
#> 9th-C6_S7 9th-C70_S42 9th-C74_S48 9th-C75_S47 9th-C77_S53 9th-C79_S57 9th-C80_S56
#> NA NA NA NA NA NA NA
#> 9th-C81_S55 9th-C83_S61 9th-C84_S60 9th-C85_S68 9th-C86_S67 9th-C87_S66 9th-C88_S73
#> NA NA NA NA NA NA NA
#> 9th-C89_S72 9th-C8_S14 9th-C91_S78 9th-C92_S77 9th-C93_S76 9th-C94_S83 9th-C96_S81
#> NA NA NA NA NA NA NA
#> 9th-C9_S13
#> NA
Heatmaps of the top rows:
top_rows_heatmap(res_rh)
Top rows on each node:
top_rows_overlap(res_rh, method = "upset")
UMAP plot which shows how samples are separated.
par(mfrow = c(1, 2))
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 181),
method = "UMAP", top_value_method = "SD", top_n = 1500, scale_rows = FALSE)
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 181),
method = "UMAP", top_value_method = "ATC", top_n = 1500, scale_rows = TRUE)

par(mfrow = c(1, 2))
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 249),
method = "UMAP", top_value_method = "SD", top_n = 1500, scale_rows = FALSE)
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 249),
method = "UMAP", top_value_method = "ATC", top_n = 1500, scale_rows = TRUE)
par(mfrow = c(1, 2))
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 256),
method = "UMAP", top_value_method = "SD", top_n = 1500, scale_rows = FALSE)
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 256),
method = "UMAP", top_value_method = "ATC", top_n = 1500, scale_rows = TRUE)
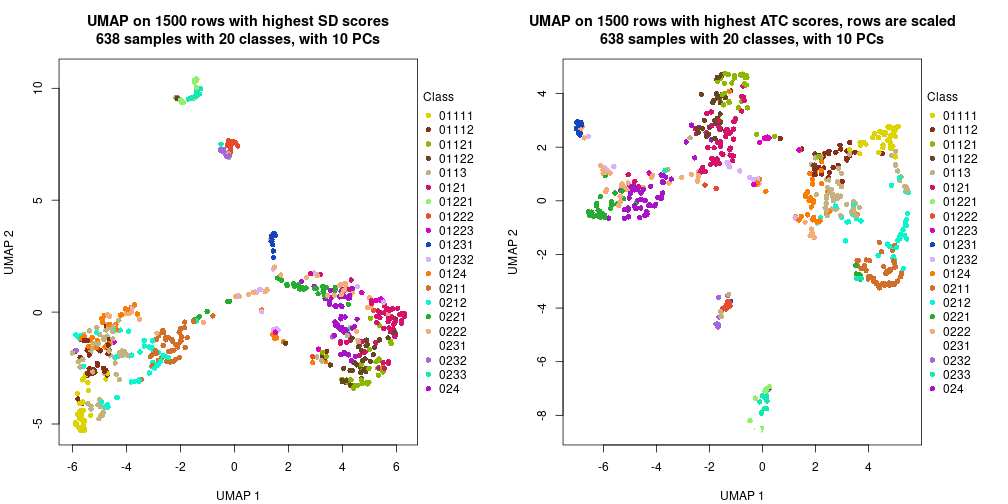
par(mfrow = c(1, 2))
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 373),
method = "UMAP", top_value_method = "SD", top_n = 1500, scale_rows = FALSE)
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 373),
method = "UMAP", top_value_method = "ATC", top_n = 1500, scale_rows = TRUE)
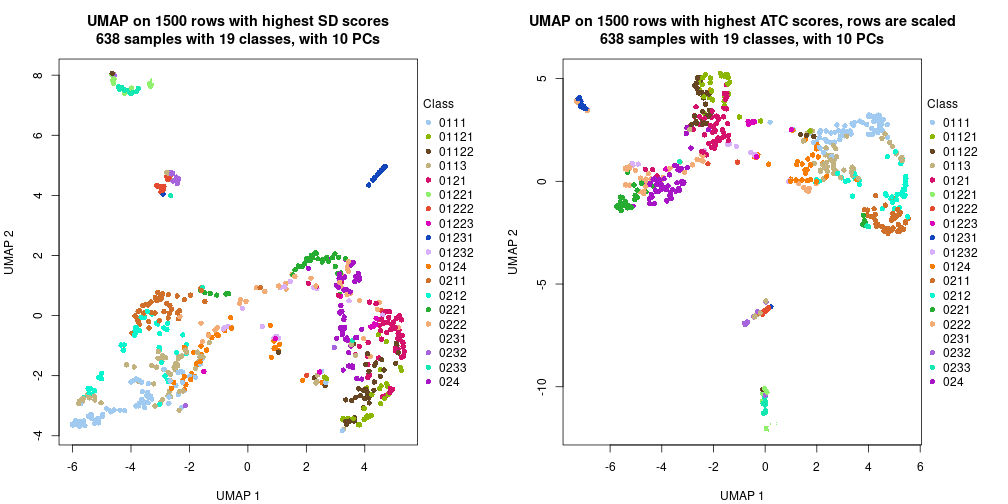
par(mfrow = c(1, 2))
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 388),
method = "UMAP", top_value_method = "SD", top_n = 1500, scale_rows = FALSE)
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 388),
method = "UMAP", top_value_method = "ATC", top_n = 1500, scale_rows = TRUE)

par(mfrow = c(1, 2))
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 507),
method = "UMAP", top_value_method = "SD", top_n = 1500, scale_rows = FALSE)
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 507),
method = "UMAP", top_value_method = "ATC", top_n = 1500, scale_rows = TRUE)
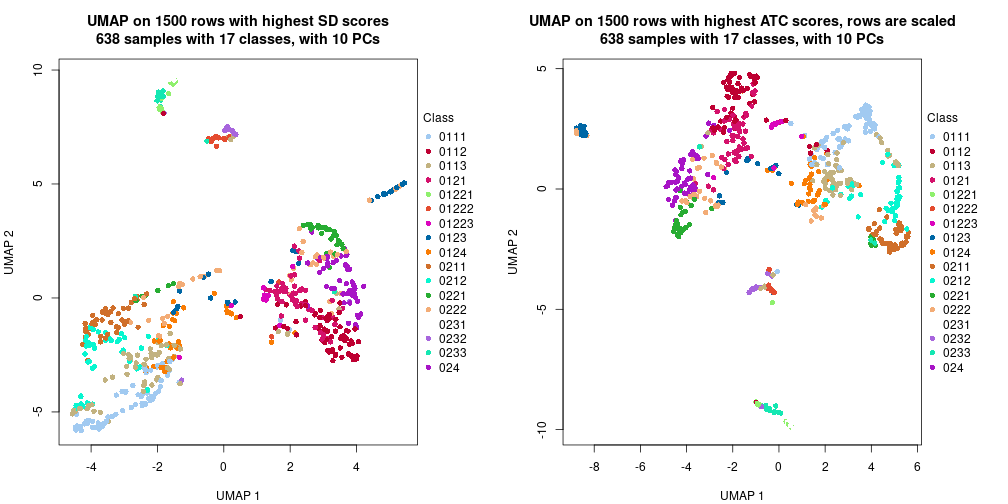
par(mfrow = c(1, 2))
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 545),
method = "UMAP", top_value_method = "SD", top_n = 1500, scale_rows = FALSE)
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 545),
method = "UMAP", top_value_method = "ATC", top_n = 1500, scale_rows = TRUE)
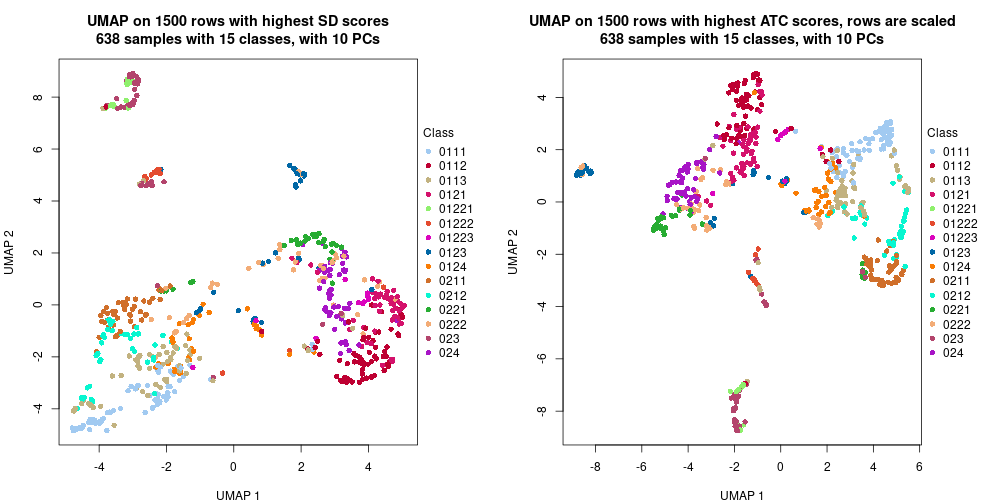
par(mfrow = c(1, 2))
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 903),
method = "UMAP", top_value_method = "SD", top_n = 1500, scale_rows = FALSE)
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 903),
method = "UMAP", top_value_method = "ATC", top_n = 1500, scale_rows = TRUE)
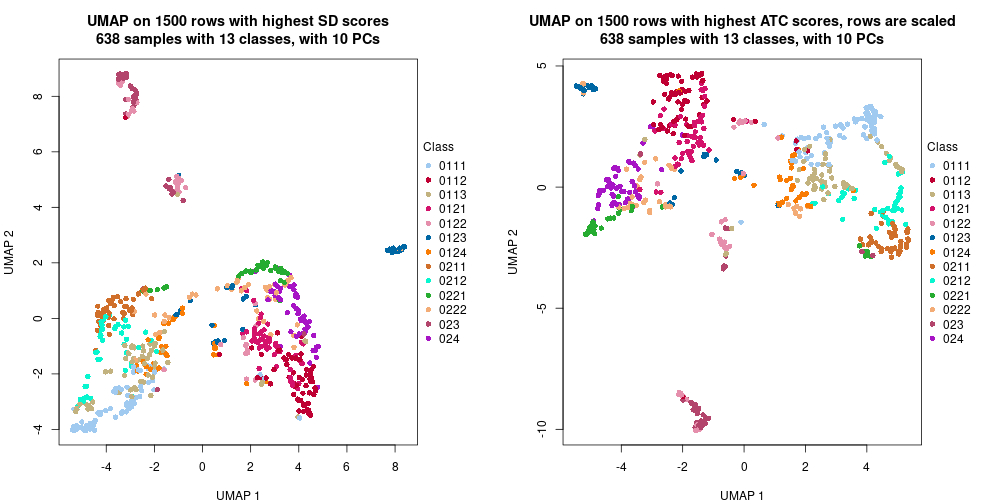
par(mfrow = c(1, 2))
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 1013),
method = "UMAP", top_value_method = "SD", top_n = 1500, scale_rows = FALSE)
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 1013),
method = "UMAP", top_value_method = "ATC", top_n = 1500, scale_rows = TRUE)
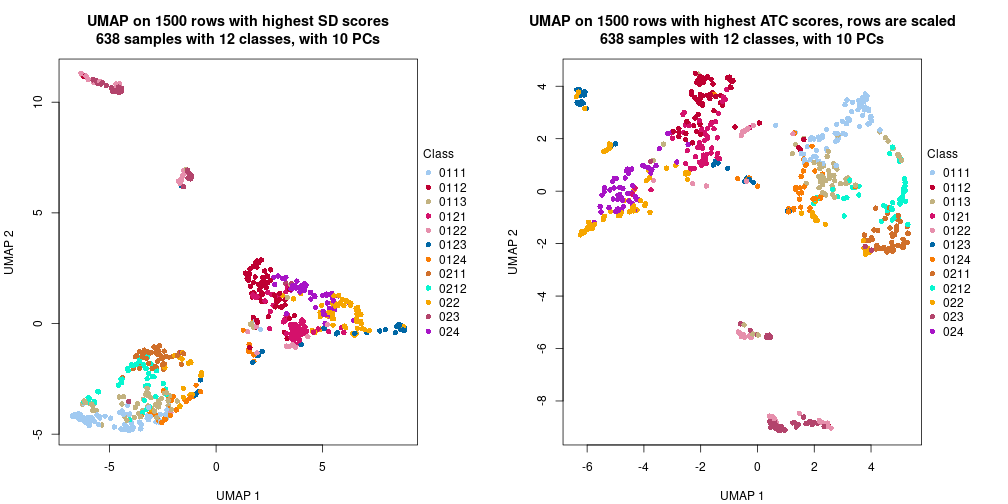
par(mfrow = c(1, 2))
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 1587),
method = "UMAP", top_value_method = "SD", top_n = 1500, scale_rows = FALSE)
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 1587),
method = "UMAP", top_value_method = "ATC", top_n = 1500, scale_rows = TRUE)
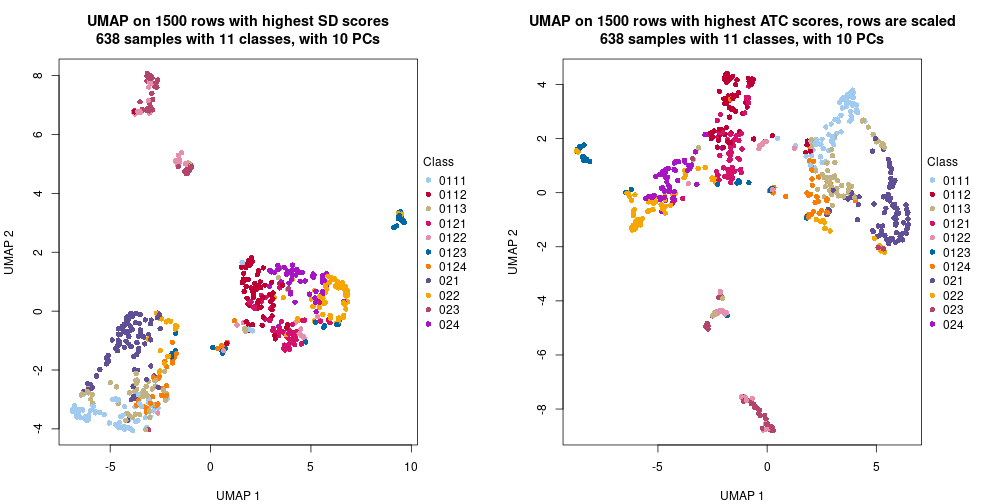
par(mfrow = c(1, 2))
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 2764),
method = "UMAP", top_value_method = "SD", top_n = 1500, scale_rows = FALSE)
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 2764),
method = "UMAP", top_value_method = "ATC", top_n = 1500, scale_rows = TRUE)
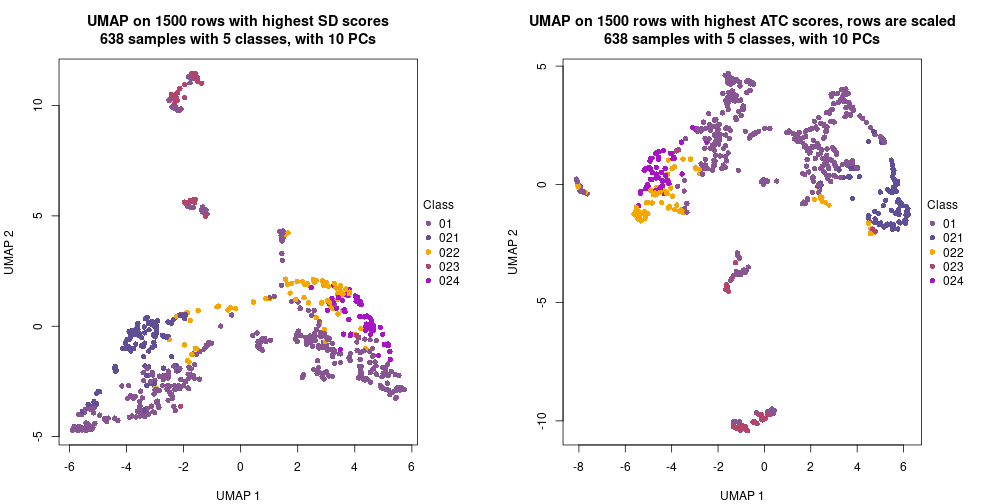
par(mfrow = c(1, 2))
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 2868),
method = "UMAP", top_value_method = "SD", top_n = 1500, scale_rows = FALSE)
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 2868),
method = "UMAP", top_value_method = "ATC", top_n = 1500, scale_rows = TRUE)
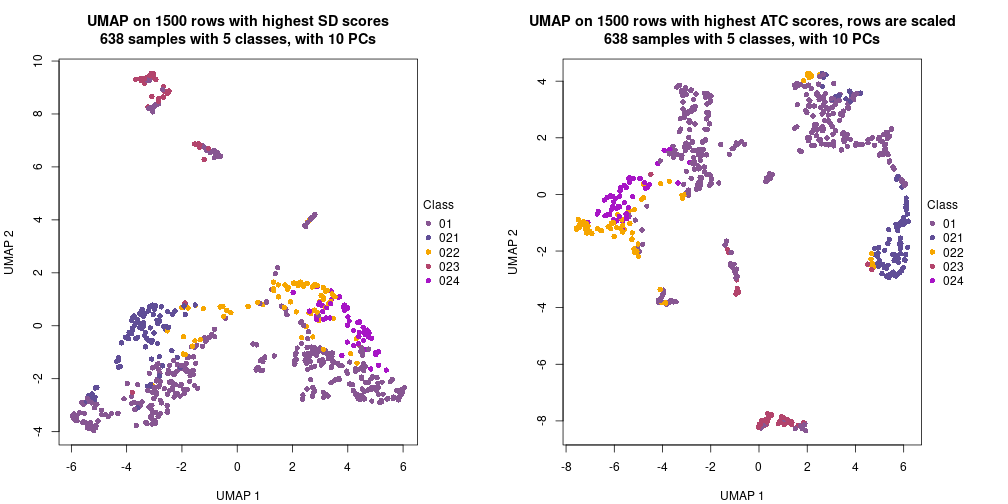
par(mfrow = c(1, 2))
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 4252),
method = "UMAP", top_value_method = "SD", top_n = 1500, scale_rows = FALSE)
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 4252),
method = "UMAP", top_value_method = "ATC", top_n = 1500, scale_rows = TRUE)
par(mfrow = c(1, 2))
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 5379),
method = "UMAP", top_value_method = "SD", top_n = 1500, scale_rows = FALSE)
dimension_reduction(res_rh, merge_node = merge_node_param(min_n_signatures = 5379),
method = "UMAP", top_value_method = "ATC", top_n = 1500, scale_rows = TRUE)
Signatures on the heatmap are the union of all signatures found on every node on the hierarchy. The number of k-means on rows are automatically selected by the function.
get_signatures(res_rh, merge_node = merge_node_param(min_n_signatures = 181))
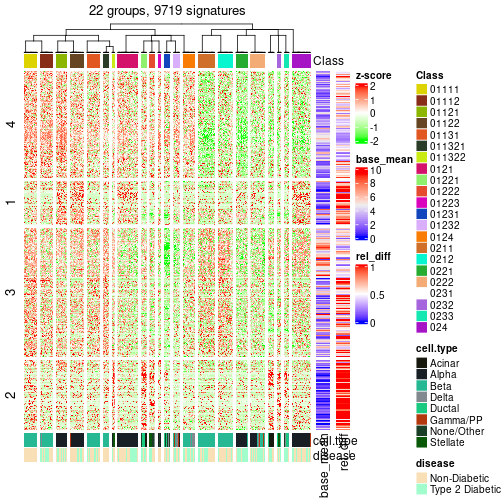
get_signatures(res_rh, merge_node = merge_node_param(min_n_signatures = 249))

get_signatures(res_rh, merge_node = merge_node_param(min_n_signatures = 256))
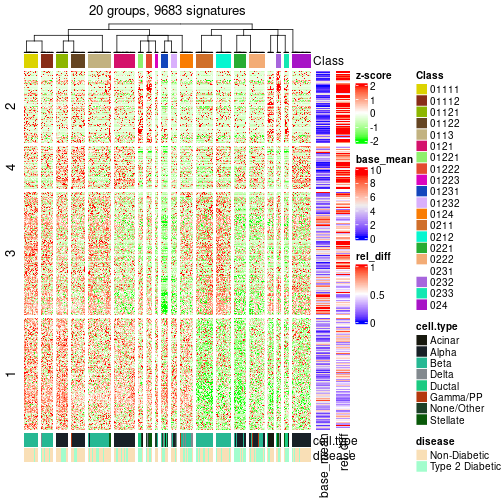
get_signatures(res_rh, merge_node = merge_node_param(min_n_signatures = 373))
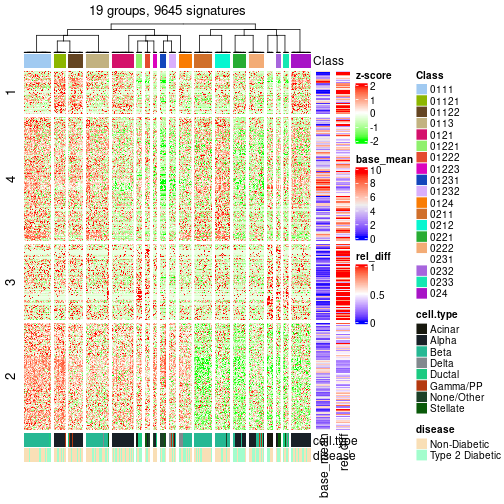
get_signatures(res_rh, merge_node = merge_node_param(min_n_signatures = 388))
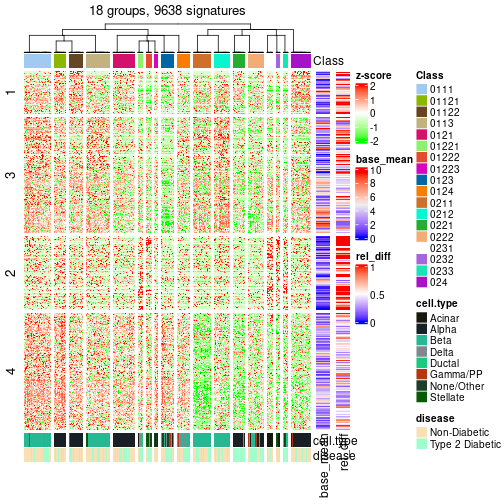
get_signatures(res_rh, merge_node = merge_node_param(min_n_signatures = 507))
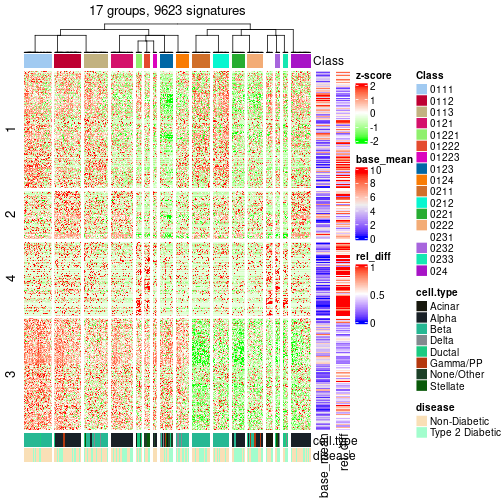
get_signatures(res_rh, merge_node = merge_node_param(min_n_signatures = 545))
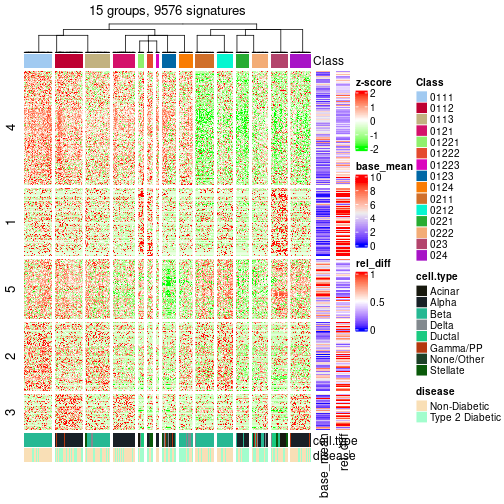
get_signatures(res_rh, merge_node = merge_node_param(min_n_signatures = 903))
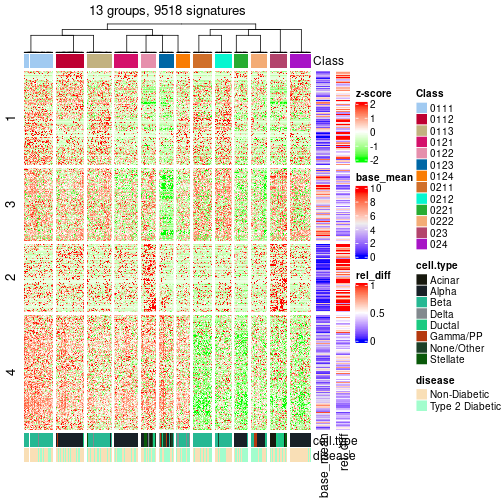
get_signatures(res_rh, merge_node = merge_node_param(min_n_signatures = 1013))
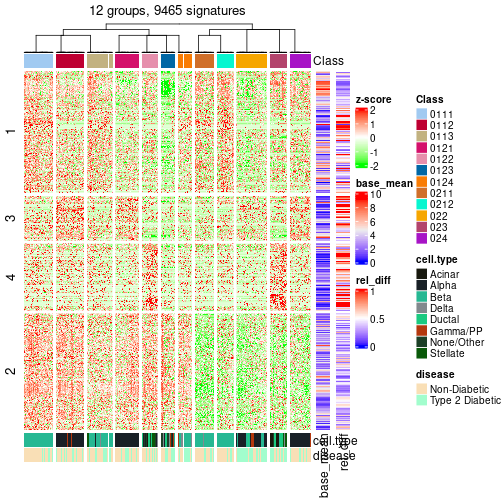
get_signatures(res_rh, merge_node = merge_node_param(min_n_signatures = 1587))
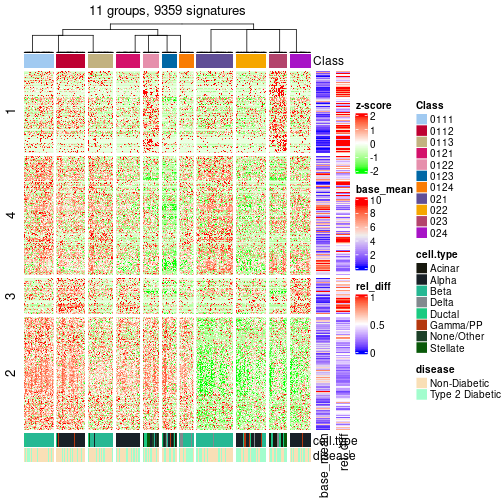
get_signatures(res_rh, merge_node = merge_node_param(min_n_signatures = 2764))
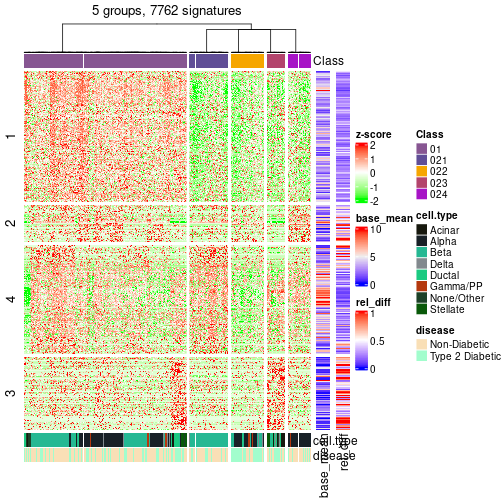
get_signatures(res_rh, merge_node = merge_node_param(min_n_signatures = 2868))
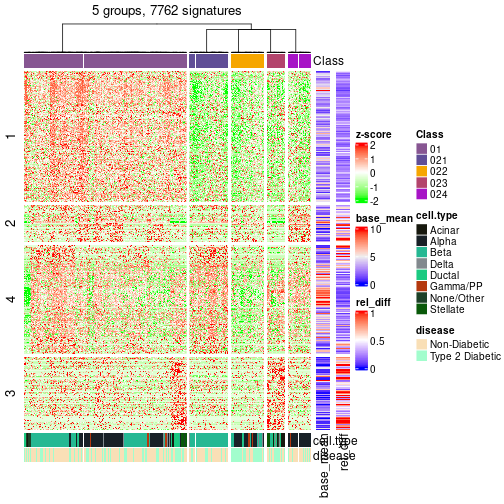
get_signatures(res_rh, merge_node = merge_node_param(min_n_signatures = 4252))
#> Error in names(x) <- value: 'names' attribute [1] must be the same length as the vector [0]
get_signatures(res_rh, merge_node = merge_node_param(min_n_signatures = 5379))
#> Error in names(x) <- value: 'names' attribute [1] must be the same length as the vector [0]
Compare signatures from different nodes:
compare_signatures(res_rh, verbose = FALSE)

If there are too many signatures, top_signatures = ... can be set to only show the
signatures with the highest FDRs. Note it only works on every node and the final signatures
are the union of all signatures of all nodes.
# code only for demonstration
# e.g. to show the top 500 most significant rows on each node.
tb = get_signature(res_rh, top_signatures = 500)
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res_rh, merge_node = merge_node_param(min_n_signatures = 181))
#> cell.type disease
#> class 1.04e-288 3.71e-10
test_to_known_factors(res_rh, merge_node = merge_node_param(min_n_signatures = 249))
#> cell.type disease
#> class 3.61e-285 3e-10
test_to_known_factors(res_rh, merge_node = merge_node_param(min_n_signatures = 256))
#> cell.type disease
#> class 2.03e-286 2.41e-10
test_to_known_factors(res_rh, merge_node = merge_node_param(min_n_signatures = 373))
#> cell.type disease
#> class 4.22e-290 9.46e-10
test_to_known_factors(res_rh, merge_node = merge_node_param(min_n_signatures = 388))
#> cell.type disease
#> class 4.85e-277 4.44e-10
test_to_known_factors(res_rh, merge_node = merge_node_param(min_n_signatures = 507))
#> cell.type disease
#> class 4.55e-281 2.01e-10
test_to_known_factors(res_rh, merge_node = merge_node_param(min_n_signatures = 545))
#> cell.type disease
#> class 4.89e-218 7.6e-11
test_to_known_factors(res_rh, merge_node = merge_node_param(min_n_signatures = 903))
#> cell.type disease
#> class 4.39e-190 9.2e-10
test_to_known_factors(res_rh, merge_node = merge_node_param(min_n_signatures = 1013))
#> cell.type disease
#> class 7.39e-190 1.08e-09
test_to_known_factors(res_rh, merge_node = merge_node_param(min_n_signatures = 1587))
#> cell.type disease
#> class 6.31e-194 8.73e-10
test_to_known_factors(res_rh, merge_node = merge_node_param(min_n_signatures = 2764))
#> cell.type disease
#> class 1.16e-89 6.44e-09
test_to_known_factors(res_rh, merge_node = merge_node_param(min_n_signatures = 2868))
#> cell.type disease
#> class 1.16e-89 6.44e-09
test_to_known_factors(res_rh, merge_node = merge_node_param(min_n_signatures = 4252))
#> cell.type disease
#> class NA NA
test_to_known_factors(res_rh, merge_node = merge_node_param(min_n_signatures = 5379))
#> cell.type disease
#> class NA NA
Child nodes: Node01 , Node02 .
The object with results only for a single top-value method and a single partitioning method can be extracted as:
res = res_rh["0"]
A summary of res and all the functions that can be applied to it:
res
#> A 'DownSamplingConsensusPartition' object with k = 2, 3, 4.
#> On a matrix with 14607 rows and 500 columns, randomly sampled from 638 columns.
#> Top rows (1388) are extracted by 'ATC' method.
#> Subgroups are detected by 'skmeans' method.
#> Performed in total 150 partitions by row resampling.
#> Best k for subgroups seems to be 4.
#>
#> Following methods can be applied to this 'DownSamplingConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_partitions"
#> [7] "compare_signatures" "consensus_heatmap" "dimension_reduction"
#> [10] "functional_enrichment" "get_anno_col" "get_anno"
#> [13] "get_classes" "get_consensus" "get_matrix"
#> [16] "get_membership" "get_param" "get_signatures"
#> [19] "get_stats" "is_best_k" "is_stable_k"
#> [22] "membership_heatmap" "ncol" "nrow"
#> [25] "plot_ecdf" "predict_classes" "rownames"
#> [28] "select_partition_number" "show" "suggest_best_k"
#> [31] "test_to_known_factors" "top_rows_heatmap"
collect_plots() function collects all the plots made from res for all k (number of subgroups)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, higher 1-PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 1.000 0.982 0.993 0.4942 0.506 0.506
#> 3 3 0.962 0.936 0.968 0.1957 0.883 0.774
#> 4 4 0.936 0.901 0.962 0.0798 0.904 0.779
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 4
#> attr(,"optional")
#> [1] 2 3
There is also optional best \(k\) = 2 3 that is worth to check.
Following is the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall subgroup
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
get_classes(res, k = 2)
#> class p
#> 10th_C10_S104 1 0.249
#> 10th_C11_S96 2 0.000
#> 10th_C13_S61 1 0.000
#> 10th_C14_S53 1 0.747
#> 10th_C16_S105 1 0.000
#> 10th_C17_S97 2 0.000
#> 10th_C19_S62 1 0.502
#> 10th_C1_S59 1 0.000
#> 10th_C20_S54 1 0.000
#> 10th_C23_S98 1 0.751
#> 10th_C24_S90 1 0.000
#> 10th_C28_S91 2 0.000
#> 10th_C30_S107 1 0.000
#> 10th_C31_S48 1 0.000
#> 10th_C32_S56 2 1.000
#> 10th_C33_S64 2 0.000
#> 10th_C34_S92 2 0.747
#> 10th_C37_S49 2 0.000
#> 10th_C41_S101 1 0.249
#> 10th_C42_S109 2 0.000
#> 10th_C43_S50 2 0.249
#> 10th_C45_S66 1 0.249
#> 10th_C46_S94 1 0.747
#> 10th_C4_S103 1 0.249
#> 10th_C50_S73 2 0.000
#> 10th_C51_S80 2 0.249
#> 10th_C52_S110 2 0.253
#> 10th_C53_S118 2 0.000
#> 10th_C54_S124 1 0.000
#> 10th_C56_S74 1 0.253
#> 10th_C57_S81 2 0.000
#> 10th_C58_S111 2 0.751
#> 10th_C5_S95 2 0.000
#> 10th_C61_S68 2 0.502
#> 10th_C63_S82 2 0.498
#> 10th_C64_S112 2 0.000
#> 10th_C66_S126 2 0.000
#> 10th_C68_S75 1 0.000
#> 10th_C6_S88 2 0.498
#> 10th_C73_S84 1 0.751
#> 10th_C74_S76 1 0.000
#> 10th_C76_S128 1 0.000
#> 10th_C77_S120 2 0.000
#> 10th_C78_S114 2 0.498
#> 10th_C7_S60 1 0.000
#> 10th_C80_S77 2 0.000
#> 10th_C81_S70 1 0.000
#> 10th_C84_S115 1 1.000
#> 10th_C85_S86 1 0.249
#> 10th_C86_S78 2 0.000
#> 10th_C87_S71 2 0.000
#> 10th_C88_S130 1 0.249
#> 10th_C8_S52 1 0.249
#> 10th_C90_S116 1 0.000
#> 10th_C95_S123 2 0.000
#> 10th_C96_S117 1 1.000
#> 11th-C10_S63 2 0.253
#> 11th-C12_S47 2 0.249
#> 11th-C16_S64 1 0.000
#> 11th-C21_S4 2 0.000
#> 11th-C22_S65 2 0.000
#> 11th-C24_S49 1 0.249
#> 11th-C26_S12 2 0.000
#> 11th-C27_S19 2 0.000
#> 11th-C2_S8 2 0.000
#> 11th-C30_S66 2 1.000
#> 11th-C33_S20 1 0.000
#> 11th-C36_S67 1 0.000
#> 11th-C37_S6 2 0.000
#> 11th-C39_S21 1 0.000
#> 11th-C40_S52 1 0.000
#> 11th-C41_S60 1 0.747
#> 11th-C43_S7 2 1.000
#> 11th-C44_S15 1 0.502
#> 11th-C49_S23 1 0.751
#> 11th-C4_S62 2 0.751
#> 11th-C51_S39 1 0.751
#> 11th-C53_S78 1 0.000
#> 11th-C54_S86 2 0.000
#> 11th-C55_S24 2 0.498
#> 11th-C56_S32 2 0.000
#> 11th-C57_S40 2 0.000
#> 11th-C58_S71 1 0.000
#> 11th-C5_S54 1 0.253
#> 11th-C61_S25 1 0.000
#> 11th-C62_S33 2 1.000
#> 11th-C64_S72 2 0.000
#> 11th-C66_S88 1 0.000
#> 11th-C67_S26 2 0.249
#> 11th-C68_S34 1 0.000
#> 11th-C77_S82 2 0.000
#> 11th-C7_S16 1 0.751
#> 11th-C93_S30 2 0.000
#> 12th-C10_S155 2 0.000
#> 12th-C11_S147 1 1.000
#> 12th-C12_S139 1 0.000
#> 12th-C14_S190 1 0.249
#> 12th-C15_S183 2 0.000
#> 12th-C1_S195 2 0.000
#> 12th-C20_S191 1 0.000
#> 12th-C21_S184 2 0.000
#> 12th-C23_S149 2 0.000
#> 12th-C24_S141 1 0.000
#> 12th-C25_S185 1 0.249
#> 12th-C26_S192 1 0.249
#> 12th-C28_S142 1 0.000
#> 12th-C29_S150 1 0.249
#> 12th-C30_S157 1 0.000
#> 12th-C33_S200 1 1.000
#> 12th-C35_S151 2 0.000
#> 12th-C36_S158 2 0.000
#> 12th-C37_S187 2 0.249
#> 12th-C38_S194 2 0.000
#> 12th-C39_S201 2 0.000
#> 12th-C3_S181 2 0.000
#> 12th-C40_S144 2 0.000
#> 12th-C42_S159 1 1.000
#> 12th-C46_S145 1 0.249
#> 12th-C47_S153 2 0.000
#> 12th-C48_S160 1 0.000
#> 12th-C4_S154 2 1.000
#> 12th-C50_S210 2 0.249
#> 12th-C51_S217 1 0.000
#> 12th-C53_S168 2 0.000
#> 12th-C55_S203 1 0.249
#> 12th-C56_S211 2 0.751
#> 12th-C57_S218 2 0.000
#> 12th-C58_S162 1 0.000
#> 12th-C59_S169 1 0.000
#> 12th-C60_S176 1 0.000
#> 12th-C63_S219 1 0.249
#> 12th-C64_S163 1 0.000
#> 12th-C65_S170 1 0.502
#> 12th-C67_S205 2 0.249
#> 12th-C69_S135 1 0.502
#> 12th-C71_S171 2 0.000
#> 12th-C74_S214 1 0.000
#> 12th-C75_S206 2 0.000
#> 12th-C76_S177 1 0.253
#> 12th-C7_S196 1 0.249
#> 12th-C80_S215 1 0.253
#> 12th-C81_S207 1 1.000
#> 12th-C84_S165 1 0.000
#> 12th-C85_S137 1 0.249
#> 12th-C8_S189 2 0.253
#> 12th-C90_S166 1 0.253
#> 12th-C93_S209 2 0.000
#> 12th-C94_S180 1 1.000
#> 12th-C95_S174 1 0.000
#> 12th-C96_S167 1 0.000
#> 13th_C12_S178 1 0.751
#> 13th_C13_S149 1 1.000
#> 13th_C15_S134 2 0.000
#> 13th_C16_S193 1 0.502
#> 13th_C17_S186 2 0.747
#> 13th_C18_S179 2 0.000
#> 13th_C1_S147 2 0.000
#> 13th_C20_S142 2 0.000
#> 13th_C21_S135 2 0.000
#> 13th_C23_S187 1 1.000
#> 13th_C27_S151 2 0.000
#> 13th_C29_S188 2 0.000
#> 13th_C31_S137 2 0.000
#> 13th_C34_S181 1 0.253
#> 13th_C36_S196 2 0.253
#> 13th_C38_S145 2 0.000
#> 13th_C39_S153 1 0.249
#> 13th_C3_S132 2 0.000
#> 13th_C46_S183 2 0.000
#> 13th_C49_S155 2 0.000
#> 13th_C4_S191 2 0.000
#> 13th_C51_S170 2 0.000
#> 13th_C52_S198 2 1.000
#> 13th_C53_S205 2 0.249
#> 13th_C54_S212 2 0.000
#> 13th_C55_S156 2 0.747
#> 13th_C57_S171 2 0.000
#> 13th_C5_S184 2 0.751
#> 13th_C60_S213 1 0.502
#> 13th_C63_S172 2 0.249
#> 13th_C66_S214 1 0.000
#> 13th_C68_S165 2 0.249
#> 13th_C69_S173 2 0.249
#> 13th_C6_S177 2 0.000
#> 13th_C70_S201 2 1.000
#> 13th_C71_S208 2 0.000
#> 13th_C72_S215 2 0.751
#> 13th_C75_S159 2 0.249
#> 13th_C76_S216 1 0.249
#> 13th_C77_S209 2 0.000
#> 13th_C79_S174 2 0.000
#> 13th_C80_S167 2 0.000
#> 13th_C81_S160 2 0.502
#> 13th_C86_S168 2 0.000
#> 13th_C88_S218 2 0.253
#> 13th_C89_S211 2 0.000
#> 13th_C8_S140 2 0.000
#> 13th_C92_S169 2 0.000
#> 13th_C93_S162 2 0.000
#> 13th_C94_S219 1 0.498
#> 13th_C96_S204 1 1.000
#> 1st-61_S27 1 0.000
#> 1st-C11_S58 1 0.000
#> 1st-C13_S19 2 0.249
#> 1st-C15_S3 2 0.253
#> 1st-C18_S51 2 0.249
#> 1st-C19_S20 1 0.498
#> 1st-C20_S12 2 0.000
#> 1st-C21_S4 1 0.249
#> 1st-C32_S14 1 1.000
#> 1st-C34_S54 1 0.000
#> 1st-C39_S23 2 0.000
#> 1st-C42_S71 1 0.000
#> 1st-C50_S33 1 0.000
#> 1st-C51_S41 2 0.000
#> 1st-C53_S74 2 0.253
#> 1st-C56_S34 1 0.000
#> 1st-C57_S42 1 0.249
#> 1st-C58_S76 1 0.498
#> 1st-C59_S77 2 0.000
#> 1st-C62_S35 2 0.751
#> 1st-C64_S79 1 0.000
#> 1st-C68_S36 1 0.000
#> 1st-C69_S44 1 0.000
#> 1st-C71_S83 1 0.000
#> 1st-C73_S45 1 0.000
#> 1st-C74_S37 2 0.000
#> 1st-C75_S29 1 0.000
#> 1st-C77_S86 1 1.000
#> 1st-C78_S85 1 0.502
#> 1st-C79_S46 2 0.249
#> 1st-C80_S38 1 0.000
#> 1st-C8_S10 2 0.000
#> 1st-C90_S91 1 0.000
#> 1st-C96_S94 2 0.000
#> 2nd-C11_S20 1 0.502
#> 2nd-C15_S25 1 0.000
#> 2nd-C16_S33 1 0.000
#> 2nd-C17_S32 1 0.000
#> 2nd-C19_S39 2 0.502
#> 2nd-C1_S3 2 0.249
#> 2nd-C21_S37 1 1.000
#> 2nd-C25_S49 1 0.000
#> 2nd-C26_S50 1 0.249
#> 2nd-C27_S51 2 0.000
#> 2nd-C28_S55 2 0.249
#> 2nd-C29_S56 1 0.000
#> 2nd-C2_S2 2 0.000
#> 2nd-C31_S61 1 0.000
#> 2nd-C32_S62 1 0.000
#> 2nd-C36_S69 2 0.000
#> 2nd-C37_S73 2 0.000
#> 2nd-C38_S74 1 0.000
#> 2nd-C39_S75 1 0.000
#> 2nd-C3_S1 2 0.000
#> 2nd-C47_S92 1 0.000
#> 2nd-C49_S4 2 0.751
#> 2nd-C4_S9 2 0.000
#> 2nd-C51_S6 2 0.249
#> 2nd-C52_S10 2 0.249
#> 2nd-C54_S12 1 0.000
#> 2nd-C57_S18 1 0.000
#> 2nd-C58_S22 2 0.000
#> 2nd-C5_S8 2 0.000
#> 2nd-C62_S29 1 0.000
#> 2nd-C67_S40 1 0.000
#> 2nd-C69_S42 2 0.000
#> 2nd-C6_S7 1 0.253
#> 2nd-C72_S48 1 0.000
#> 2nd-C74_S53 1 0.000
#> 2nd-C75_S52 1 0.000
#> 2nd-C76_S60 1 0.000
#> 2nd-C77_S59 1 0.751
#> 2nd-C7_S15 2 0.000
#> 2nd-C80_S65 1 0.000
#> 2nd-C81_S64 1 0.000
#> 2nd-C83_S71 1 0.000
#> 2nd-C86_S77 1 0.000
#> 2nd-C87_S76 2 0.249
#> 2nd-C88_S84 1 0.000
#> 2nd-C8_S14 1 1.000
#> 2nd-C93_S88 1 0.249
#> 2nd-C94_S96 2 0.000
#> 2nd-C95_S95 1 0.000
#> 3rd-C11_S58 1 0.000
#> 3rd-C12_S68 1 1.000
#> 3rd-C18_S80 1 0.000
#> 3rd-C1_S39 1 0.000
#> 3rd-C20_S22 1 0.000
#> 3rd-C21_S11 1 0.000
#> 3rd-C23_S94 2 0.249
#> 3rd-C25_S15 2 0.000
#> 3rd-C26_S28 1 0.000
#> 3rd-C27_S49 1 0.000
#> 3rd-C32_S31 2 0.000
#> 3rd-C33_S50 1 0.498
#> 3rd-C35_S23 1 1.000
#> 3rd-C36_S2 1 0.000
#> 3rd-C3_S2 2 0.000
#> 3rd-C40_S57 1 0.000
#> 3rd-C42_S74 1 0.000
#> 3rd-C44_S32 2 1.000
#> 3rd-C46_S93 1 0.000
#> 3rd-C47_S35 1 0.000
#> 3rd-C49_S60 1 0.000
#> 3rd-C4_S25 1 1.000
#> 3rd-C51_S87 2 0.000
#> 3rd-C52_S86 2 0.000
#> 3rd-C53_S67 1 0.000
#> 3rd-C56_S90 2 0.751
#> 3rd-C57_S5 1 0.000
#> 3rd-C58_S3 1 0.000
#> 3rd-C59_S91 1 0.000
#> 3rd-C60_S10 2 0.000
#> 3rd-C61_S64 2 0.253
#> 3rd-C63_S54 2 0.000
#> 3rd-C65_S20 1 0.000
#> 3rd-C67_S69 1 0.249
#> 3rd-C68_S13 1 0.000
#> 3rd-C69_S78 2 0.249
#> 3rd-C6_S44 1 0.502
#> 3rd-C71_S80 1 0.000
#> 3rd-C76_S22 1 0.000
#> 3rd-C79_S67 1 0.000
#> 3rd-C7_S40 2 0.000
#> 3rd-C82_S11 1 0.249
#> 3rd-C84_S75 1 0.000
#> 3rd-C85_S79 1 0.502
#> 3rd-C85_S83 2 0.000
#> 3rd-C86_S85 1 0.747
#> 3rd-C87_S88 1 0.751
#> 3rd-C88_S24 1 0.000
#> 3rd-C91_S91 1 0.000
#> 3rd-C92_S86 1 0.000
#> 3rd-C95_S81 1 0.000
#> 3rd-C96_S79 2 0.000
#> 3rd-C9_S5 1 1.000
#> 4th-61_S28 1 0.000
#> 4th-C12_S19 1 0.000
#> 4th-C14_S26 1 0.000
#> 4th-C18_S31 1 0.249
#> 4th-C22_S45 2 0.249
#> 4th-C23_S44 1 0.000
#> 4th-C24_S43 1 0.000
#> 4th-C26_S50 1 0.000
#> 4th-C27_S51 2 1.000
#> 4th-C28_S55 1 0.000
#> 4th-C29_S56 1 0.000
#> 4th-C32_S62 1 0.000
#> 4th-C33_S63 1 0.249
#> 4th-C35_S68 2 0.000
#> 4th-C36_S69 1 0.000
#> 4th-C37_S73 2 0.751
#> 4th-C3_S1 2 0.000
#> 4th-C40_S79 1 0.000
#> 4th-C43_S85 1 0.000
#> 4th-C45_S87 2 0.253
#> 4th-C49_S4 1 0.498
#> 4th-C4_S9 1 0.000
#> 4th-C50_S5 2 0.000
#> 4th-C51_S6 1 0.000
#> 4th-C56_S17 1 0.000
#> 4th-C57_S18 2 0.249
#> 4th-C59_S23 1 0.000
#> 4th-C5_S8 1 0.000
#> 4th-C62_S29 1 0.000
#> 4th-C63_S30 1 0.000
#> 4th-C64_S34 1 0.000
#> 4th-C66_S36 1 0.000
#> 4th-C67_S40 1 0.249
#> 4th-C68_S41 2 0.751
#> 4th-C69_S42 1 0.000
#> 4th-C70_S46 1 0.000
#> 4th-C73_S54 1 0.000
#> 4th-C75_S52 1 0.000
#> 4th-C78_S58 1 0.000
#> 4th-C79_S66 1 0.000
#> 4th-C7_S15 1 0.000
#> 4th-C80_S65 1 0.000
#> 4th-C81_S64 1 0.000
#> 4th-C82_S72 1 0.000
#> 4th-C83_S71 1 1.000
#> 4th-C85_S78 1 0.000
#> 4th-C86_S77 1 0.000
#> 4th-C87_S76 1 0.000
#> 4th-C88_S84 1 0.000
#> 4th-C89_S83 1 0.000
#> 4th-C8_S14 1 0.000
#> 4th-C92_S89 1 0.000
#> 4th-C93_S88 2 0.000
#> 4th-C94_S96 1 0.253
#> 4th-C95_S95 1 0.000
#> 4th-C96_S94 1 0.000
#> 4th-C9_S13 2 0.249
#> 5th-C10_S92 2 0.000
#> 5th-C11_S91 2 0.751
#> 5th-C12_S90 1 0.000
#> 5th-C14_S97 2 0.000
#> 5th-C16_S98 2 0.751
#> 5th-C18_S96 2 0.000
#> 5th-C19_S104 1 0.000
#> 5th-C21_S102 1 0.000
#> 5th-C25_S108 2 0.000
#> 5th-C30_S105 1 0.000
#> 5th-C34_S108 1 0.000
#> 5th-C35_S109 1 0.000
#> 5th-C40_S112 2 0.000
#> 5th-C41_S113 2 0.751
#> 5th-C42_S114 2 0.000
#> 5th-C43_S121 2 0.747
#> 5th-C45_S123 2 0.000
#> 5th-C47_S118 1 0.751
#> 5th-C49_S89 1 0.000
#> 5th-C50_S90 1 0.000
#> 5th-C54_S89 1 0.000
#> 5th-C56_S95 2 0.000
#> 5th-C57_S96 1 0.000
#> 5th-C58_S93 2 0.249
#> 5th-C59_S94 1 0.000
#> 5th-C5_S85 1 0.000
#> 5th-C64_S99 1 0.000
#> 5th-C66_S101 1 0.000
#> 5th-C67_S105 2 0.000
#> 5th-C68_S106 1 0.000
#> 5th-C69_S107 1 0.000
#> 5th-C6_S84 2 0.253
#> 5th-C70_S103 2 0.000
#> 5th-C73_S111 2 0.000
#> 5th-C74_S110 1 0.000
#> 5th-C77_S107 1 0.249
#> 5th-C7_S93 1 0.000
#> 5th-C80_S116 2 0.249
#> 5th-C81_S115 2 0.000
#> 5th-C83_S111 2 0.000
#> 5th-C87_S119 2 0.498
#> 5th-C88_S117 2 0.249
#> 5th-C90_S115 1 0.747
#> 5th-C92_S124 1 0.000
#> 5th-C9_S92 1 0.000
#> 6th-C12_S18 1 0.000
#> 6th-C15_S22 2 0.000
#> 6th-C16_S29 1 0.000
#> 6th-C19_S35 2 0.000
#> 6th-C1_S3 2 0.000
#> 6th-C20_S34 1 0.249
#> 6th-C21_S33 1 0.000
#> 6th-C22_S39 1 0.498
#> 6th-C23_S38 1 0.000
#> 6th-C24_S37 1 0.253
#> 6th-C25_S43 2 0.751
#> 6th-C28_S49 2 0.000
#> 6th-C29_S50 1 0.000
#> 6th-C2_S2 1 0.249
#> 6th-C30_S51 1 0.498
#> 6th-C34_S61 2 0.000
#> 6th-C40_S73 1 0.502
#> 6th-C42_S75 1 0.000
#> 6th-C45_S81 2 0.000
#> 6th-C51_S6 1 1.000
#> 6th-C53_S10 1 0.000
#> 6th-C54_S11 1 0.000
#> 6th-C57_S17 2 0.000
#> 6th-C58_S20 2 0.249
#> 6th-C59_S21 1 0.000
#> 6th-C5_S8 1 0.000
#> 6th-C62_S25 2 0.000
#> 6th-C63_S26 1 0.000
#> 6th-C64_S30 2 0.000
#> 6th-C65_S31 1 0.000
#> 6th-C66_S32 1 0.249
#> 6th-C67_S36 2 0.000
#> 6th-C71_S41 1 0.000
#> 6th-C73_S48 1 1.000
#> 6th-C75_S46 1 1.000
#> 6th-C77_S53 1 0.000
#> 6th-C79_S60 1 0.000
#> 6th-C80_S59 1 0.253
#> 6th-C82_S66 2 0.000
#> 6th-C83_S65 2 0.000
#> 6th-C84_S64 2 0.000
#> 6th-C85_S72 1 0.000
#> 6th-C87_S70 1 0.000
#> 6th-C89_S77 2 0.000
#> 6th-C90_S76 2 0.000
#> 6th-C91_S84 1 0.000
#> 6th-C93_S82 1 0.000
#> 6th-C9_S12 2 0.000
#> 7th-C10_S19 1 0.498
#> 7th-C11_S18 1 1.000
#> 7th-C12_S17 2 0.253
#> 7th-C14_S24 1 0.000
#> 7th-C15_S23 1 0.502
#> 7th-C17_S29 1 0.000
#> 7th-C19_S36 2 0.000
#> 7th-C1_S3 2 0.000
#> 7th-C20_S35 2 0.000
#> 7th-C21_S34 2 0.000
#> 7th-C24_S40 1 0.000
#> 7th-C25_S43 1 0.000
#> 7th-C28_S48 2 0.000
#> 7th-C2_S2 2 0.000
#> 7th-C31_S53 1 0.000
#> 7th-C32_S54 1 0.498
#> 7th-C34_S59 1 0.000
#> 7th-C36_S61 1 0.000
#> 7th-C3_S1 2 0.000
#> 7th-C40_S70 1 0.000
#> 7th-C44_S76 1 0.000
#> 7th-C45_S77 1 0.000
#> 7th-C47_S81 2 0.498
#> 7th-C49_S4 2 0.000
#> 7th-C4_S8 2 0.000
#> 7th-C50_S5 1 0.000
#> 7th-C52_S9 2 0.000
#> 7th-C53_S10 1 0.000
#> 7th-C56_S15 1 0.000
#> 7th-C57_S16 2 0.747
#> 7th-C58_S20 1 0.000
#> 7th-C59_S21 1 0.000
#> 7th-C60_S22 2 0.249
#> 7th-C62_S27 1 0.000
#> 7th-C64_S31 1 0.000
#> 7th-C65_S32 2 0.249
#> 7th-C66_S33 1 0.000
#> 7th-C68_S38 1 0.000
#> 7th-C69_S39 1 0.000
#> 7th-C72_S42 1 0.000
#> 7th-C73_S47 1 0.751
#> 7th-C76_S52 2 0.000
#> 7th-C77_S51 1 0.000
#> 7th-C79_S58 1 0.751
#> 7th-C80_S57 1 0.502
#> 7th-C81_S56 2 0.751
#> 7th-C82_S64 1 0.000
#> 7th-C84_S62 1 0.000
#> 7th-C85_S69 2 0.000
#> 7th-C88_S75 1 0.000
#> 7th-C89_S74 1 0.000
#> 7th-C8_S13 1 0.000
#> 7th-C90_S73 1 0.000
#> 7th-C94_S83 2 0.000
#> 7th-C96_S82 1 0.000
#> 8th-C10_S100 1 0.000
#> 8th-C11_S99 1 0.000
#> 8th-C18_S110 2 0.249
#> 8th-C20_S116 1 0.000
#> 8th-C21_S115 2 0.000
#> 8th-C23_S121 2 0.000
#> 8th-C24_S120 1 0.000
#> 8th-C26_S126 2 0.000
#> 8th-C28_S131 2 0.253
#> 8th-C2_S85 1 0.000
#> 8th-C34_S141 1 0.751
#> 8th-C37_S146 2 0.000
#> 8th-C38_S147 2 0.000
#> 8th-C44_S155 1 0.000
#> 8th-C47_S160 2 0.000
#> 8th-C55_S96 1 0.498
#> 8th-C57_S98 1 1.000
#> 8th-C58_S101 1 0.000
#> 8th-C59_S102 1 0.249
#> 8th-C61_S107 1 0.000
#> 8th-C64_S112 1 0.000
#> 8th-C65_S113 1 0.000
#> 8th-C67_S117 1 0.249
#> 8th-C69_S119 2 0.000
#> 8th-C6_S88 1 0.000
#> 8th-C70_S123 2 0.000
#> 8th-C73_S130 1 0.000
#> 8th-C74_S129 1 0.000
#> 8th-C75_S128 2 0.000
#> 8th-C79_S140 2 0.000
#> 8th-C7_S95 1 0.000
#> 8th-C84_S143 2 0.000
#> 8th-C85_S150 1 0.000
#> 8th-C87_S148 1 0.000
#> 8th-C90_S152 2 0.000
#> 8th-C91_S158 2 1.000
#> 8th-C92_S157 1 0.000
#> 8th-C94_S162 2 0.000
#> 8th-C95_S161 1 0.000
#> 9th-C10_S18 1 0.000
#> 9th-C11_S17 1 0.000
#> 9th-C13_S24 2 0.249
#> 9th-C14_S23 2 0.000
#> 9th-C15_S22 1 0.000
#> 9th-C16_S30 1 0.000
#> 9th-C17_S29 1 0.498
#> 9th-C19_S36 1 0.000
#> 9th-C1_S3 1 0.000
#> 9th-C20_S35 2 0.000
#> 9th-C22_S41 2 0.000
#> 9th-C25_S45 2 0.000
#> 9th-C28_S50 1 0.000
#> 9th-C29_S51 1 0.000
#> 9th-C2_S2 2 0.000
#> 9th-C30_S52 1 0.000
#> 9th-C36_S59 1 0.000
#> 9th-C38_S64 1 1.000
#> 9th-C3_S1 1 0.000
#> 9th-C40_S69 1 0.253
#> 9th-C41_S70 1 0.000
#> 9th-C46_S79 1 0.249
#> 9th-C49_S4 2 0.000
#> 9th-C51_S6 2 0.000
#> 9th-C52_S10 2 0.747
#> 9th-C57_S16 1 0.249
#> 9th-C59_S20 2 0.000
#> 9th-C5_S8 1 0.000
#> 9th-C61_S25 1 0.751
#> 9th-C62_S26 1 0.000
#> 9th-C64_S31 1 0.000
#> 9th-C65_S32 1 0.000
#> 9th-C66_S33 1 0.000
#> 9th-C67_S37 1 0.000
#> 9th-C69_S39 2 0.000
#> 9th-C6_S7 1 0.253
#> 9th-C70_S42 1 0.249
#> 9th-C74_S48 1 0.000
#> 9th-C75_S47 2 0.000
#> 9th-C77_S53 1 0.000
#> 9th-C79_S57 2 0.000
#> 9th-C80_S56 1 0.502
#> 9th-C81_S55 1 0.253
#> 9th-C83_S61 1 0.000
#> 9th-C84_S60 1 0.000
#> 9th-C85_S68 2 1.000
#> 9th-C86_S67 1 0.000
#> 9th-C87_S66 2 0.000
#> 9th-C88_S73 2 0.000
#> 9th-C89_S72 1 0.000
#> 9th-C8_S14 1 0.253
#> 9th-C91_S78 2 0.000
#> 9th-C92_S77 2 0.000
#> 9th-C93_S76 1 0.249
#> 9th-C94_S83 2 0.000
#> 9th-C96_S81 1 0.000
#> 9th-C9_S13 1 0.502
get_classes(res, k = 3)
#> class p
#> 10th_C10_S104 3 0.000
#> 10th_C11_S96 2 0.000
#> 10th_C13_S61 1 0.000
#> 10th_C14_S53 1 0.249
#> 10th_C16_S105 1 0.253
#> 10th_C17_S97 2 0.000
#> 10th_C19_S62 3 0.000
#> 10th_C1_S59 1 0.000
#> 10th_C20_S54 1 0.000
#> 10th_C23_S98 3 0.000
#> 10th_C24_S90 3 0.502
#> 10th_C28_S91 3 1.000
#> 10th_C30_S107 1 0.502
#> 10th_C31_S48 3 0.000
#> 10th_C32_S56 2 0.253
#> 10th_C33_S64 2 0.000
#> 10th_C34_S92 3 1.000
#> 10th_C37_S49 2 0.000
#> 10th_C41_S101 3 0.249
#> 10th_C42_S109 2 0.000
#> 10th_C43_S50 2 0.000
#> 10th_C45_S66 3 0.000
#> 10th_C46_S94 3 0.498
#> 10th_C4_S103 3 0.000
#> 10th_C50_S73 2 0.000
#> 10th_C51_S80 2 0.249
#> 10th_C52_S110 2 0.498
#> 10th_C53_S118 2 0.000
#> 10th_C54_S124 1 1.000
#> 10th_C56_S74 1 1.000
#> 10th_C57_S81 2 0.249
#> 10th_C58_S111 3 0.253
#> 10th_C5_S95 2 0.000
#> 10th_C61_S68 2 0.249
#> 10th_C63_S82 2 1.000
#> 10th_C64_S112 2 0.000
#> 10th_C66_S126 2 0.000
#> 10th_C68_S75 3 0.000
#> 10th_C6_S88 3 0.249
#> 10th_C73_S84 3 0.000
#> 10th_C74_S76 1 0.253
#> 10th_C76_S128 1 0.253
#> 10th_C77_S120 2 0.249
#> 10th_C78_S114 2 0.249
#> 10th_C7_S60 1 1.000
#> 10th_C80_S77 2 0.000
#> 10th_C81_S70 3 0.000
#> 10th_C84_S115 1 0.747
#> 10th_C85_S86 3 1.000
#> 10th_C86_S78 2 0.249
#> 10th_C87_S71 2 0.498
#> 10th_C88_S130 3 0.000
#> 10th_C8_S52 3 0.249
#> 10th_C90_S116 1 0.000
#> 10th_C95_S123 2 0.249
#> 10th_C96_S117 3 1.000
#> 11th-C10_S63 2 0.249
#> 11th-C12_S47 3 0.751
#> 11th-C16_S64 1 1.000
#> 11th-C21_S4 2 0.000
#> 11th-C22_S65 2 0.253
#> 11th-C24_S49 3 0.000
#> 11th-C26_S12 2 1.000
#> 11th-C27_S19 2 0.000
#> 11th-C2_S8 2 0.249
#> 11th-C30_S66 2 1.000
#> 11th-C33_S20 3 0.000
#> 11th-C36_S67 1 1.000
#> 11th-C37_S6 2 0.000
#> 11th-C39_S21 1 0.000
#> 11th-C40_S52 3 0.498
#> 11th-C41_S60 1 0.751
#> 11th-C43_S7 3 0.000
#> 11th-C44_S15 3 1.000
#> 11th-C49_S23 3 1.000
#> 11th-C4_S62 3 0.000
#> 11th-C51_S39 3 1.000
#> 11th-C53_S78 1 0.000
#> 11th-C54_S86 3 0.751
#> 11th-C55_S24 2 0.751
#> 11th-C56_S32 2 0.000
#> 11th-C57_S40 2 0.000
#> 11th-C58_S71 1 1.000
#> 11th-C5_S54 3 0.249
#> 11th-C61_S25 1 0.249
#> 11th-C62_S33 3 0.249
#> 11th-C64_S72 3 0.000
#> 11th-C66_S88 1 0.000
#> 11th-C67_S26 2 0.253
#> 11th-C68_S34 3 0.000
#> 11th-C77_S82 2 1.000
#> 11th-C7_S16 3 0.000
#> 11th-C93_S30 2 0.000
#> 12th-C10_S155 2 0.000
#> 12th-C11_S147 3 0.751
#> 12th-C12_S139 3 1.000
#> 12th-C14_S190 1 1.000
#> 12th-C15_S183 2 0.000
#> 12th-C1_S195 2 0.000
#> 12th-C20_S191 1 1.000
#> 12th-C21_S184 2 0.000
#> 12th-C23_S149 2 0.000
#> 12th-C24_S141 3 1.000
#> 12th-C25_S185 3 1.000
#> 12th-C26_S192 3 1.000
#> 12th-C28_S142 1 0.249
#> 12th-C29_S150 1 0.000
#> 12th-C30_S157 1 0.000
#> 12th-C33_S200 3 0.000
#> 12th-C35_S151 2 0.000
#> 12th-C36_S158 2 0.502
#> 12th-C37_S187 2 0.751
#> 12th-C38_S194 2 0.000
#> 12th-C39_S201 2 0.000
#> 12th-C3_S181 2 0.000
#> 12th-C40_S144 2 0.000
#> 12th-C42_S159 3 1.000
#> 12th-C46_S145 1 1.000
#> 12th-C47_S153 2 0.000
#> 12th-C48_S160 1 1.000
#> 12th-C4_S154 2 0.502
#> 12th-C50_S210 2 0.000
#> 12th-C51_S217 3 1.000
#> 12th-C53_S168 3 1.000
#> 12th-C55_S203 3 0.502
#> 12th-C56_S211 3 0.000
#> 12th-C57_S218 2 0.000
#> 12th-C58_S162 1 0.000
#> 12th-C59_S169 1 0.000
#> 12th-C60_S176 1 0.000
#> 12th-C63_S219 3 0.000
#> 12th-C64_S163 1 0.000
#> 12th-C65_S170 3 1.000
#> 12th-C67_S205 2 0.249
#> 12th-C69_S135 3 0.000
#> 12th-C71_S171 2 0.249
#> 12th-C74_S214 1 0.249
#> 12th-C75_S206 2 0.000
#> 12th-C76_S177 1 0.253
#> 12th-C7_S196 3 1.000
#> 12th-C80_S215 3 0.253
#> 12th-C81_S207 3 0.000
#> 12th-C84_S165 1 0.751
#> 12th-C85_S137 3 0.000
#> 12th-C8_S189 2 0.498
#> 12th-C90_S166 1 0.000
#> 12th-C93_S209 2 0.000
#> 12th-C94_S180 3 0.000
#> 12th-C95_S174 1 0.000
#> 12th-C96_S167 1 0.000
#> 13th_C12_S178 3 1.000
#> 13th_C13_S149 3 0.000
#> 13th_C15_S134 3 1.000
#> 13th_C16_S193 3 1.000
#> 13th_C17_S186 3 1.000
#> 13th_C18_S179 2 0.253
#> 13th_C1_S147 2 0.000
#> 13th_C20_S142 2 0.000
#> 13th_C21_S135 2 0.000
#> 13th_C23_S187 3 0.000
#> 13th_C27_S151 2 0.249
#> 13th_C29_S188 2 0.000
#> 13th_C31_S137 2 1.000
#> 13th_C34_S181 3 1.000
#> 13th_C36_S196 2 0.000
#> 13th_C38_S145 2 0.000
#> 13th_C39_S153 3 0.502
#> 13th_C3_S132 2 0.000
#> 13th_C46_S183 2 0.000
#> 13th_C49_S155 2 1.000
#> 13th_C4_S191 2 0.000
#> 13th_C51_S170 2 0.000
#> 13th_C52_S198 2 1.000
#> 13th_C53_S205 2 1.000
#> 13th_C54_S212 2 0.000
#> 13th_C55_S156 2 0.249
#> 13th_C57_S171 2 0.000
#> 13th_C5_S184 2 0.000
#> 13th_C60_S213 3 0.000
#> 13th_C63_S172 3 0.249
#> 13th_C66_S214 1 0.249
#> 13th_C68_S165 2 0.000
#> 13th_C69_S173 2 1.000
#> 13th_C6_S177 2 0.000
#> 13th_C70_S201 3 0.751
#> 13th_C71_S208 3 0.751
#> 13th_C72_S215 3 0.502
#> 13th_C75_S159 2 0.253
#> 13th_C76_S216 3 1.000
#> 13th_C77_S209 2 0.000
#> 13th_C79_S174 3 1.000
#> 13th_C80_S167 2 0.000
#> 13th_C81_S160 3 1.000
#> 13th_C86_S168 2 0.000
#> 13th_C88_S218 3 0.000
#> 13th_C89_S211 2 0.000
#> 13th_C8_S140 2 0.000
#> 13th_C92_S169 2 0.000
#> 13th_C93_S162 2 0.000
#> 13th_C94_S219 3 0.747
#> 13th_C96_S204 3 1.000
#> 1st-61_S27 1 0.751
#> 1st-C11_S58 1 0.000
#> 1st-C13_S19 2 0.498
#> 1st-C15_S3 2 0.000
#> 1st-C18_S51 2 0.747
#> 1st-C19_S20 3 0.498
#> 1st-C20_S12 2 0.249
#> 1st-C21_S4 3 0.249
#> 1st-C32_S14 3 1.000
#> 1st-C34_S54 3 1.000
#> 1st-C39_S23 2 0.498
#> 1st-C42_S71 1 0.751
#> 1st-C50_S33 1 0.751
#> 1st-C51_S41 2 0.000
#> 1st-C53_S74 2 0.000
#> 1st-C56_S34 1 0.000
#> 1st-C57_S42 1 1.000
#> 1st-C58_S76 1 1.000
#> 1st-C59_S77 3 1.000
#> 1st-C62_S35 2 1.000
#> 1st-C64_S79 1 1.000
#> 1st-C68_S36 1 0.502
#> 1st-C69_S44 1 0.751
#> 1st-C71_S83 3 1.000
#> 1st-C73_S45 3 1.000
#> 1st-C74_S37 2 1.000
#> 1st-C75_S29 1 0.000
#> 1st-C77_S86 3 1.000
#> 1st-C78_S85 3 1.000
#> 1st-C79_S46 2 0.751
#> 1st-C80_S38 1 0.000
#> 1st-C8_S10 2 0.000
#> 1st-C90_S91 1 0.249
#> 1st-C96_S94 2 0.000
#> 2nd-C11_S20 1 0.751
#> 2nd-C15_S25 1 0.000
#> 2nd-C16_S33 1 0.000
#> 2nd-C17_S32 1 0.000
#> 2nd-C19_S39 2 0.000
#> 2nd-C1_S3 2 1.000
#> 2nd-C21_S37 3 0.000
#> 2nd-C25_S49 1 0.000
#> 2nd-C26_S50 1 0.000
#> 2nd-C27_S51 2 0.000
#> 2nd-C28_S55 3 0.751
#> 2nd-C29_S56 1 0.000
#> 2nd-C2_S2 2 0.502
#> 2nd-C31_S61 1 1.000
#> 2nd-C32_S62 1 0.000
#> 2nd-C36_S69 2 0.000
#> 2nd-C37_S73 2 0.000
#> 2nd-C38_S74 1 0.249
#> 2nd-C39_S75 1 0.000
#> 2nd-C3_S1 2 0.000
#> 2nd-C47_S92 1 0.253
#> 2nd-C49_S4 2 0.000
#> 2nd-C4_S9 2 0.249
#> 2nd-C51_S6 2 0.498
#> 2nd-C52_S10 2 0.249
#> 2nd-C54_S12 1 1.000
#> 2nd-C57_S18 1 0.000
#> 2nd-C58_S22 3 0.502
#> 2nd-C5_S8 2 0.249
#> 2nd-C62_S29 1 0.249
#> 2nd-C67_S40 1 0.751
#> 2nd-C69_S42 2 0.000
#> 2nd-C6_S7 3 1.000
#> 2nd-C72_S48 1 0.498
#> 2nd-C74_S53 1 0.000
#> 2nd-C75_S52 1 1.000
#> 2nd-C76_S60 1 0.000
#> 2nd-C77_S59 3 1.000
#> 2nd-C7_S15 2 0.000
#> 2nd-C80_S65 1 0.498
#> 2nd-C81_S64 3 1.000
#> 2nd-C83_S71 3 0.000
#> 2nd-C86_S77 3 0.249
#> 2nd-C87_S76 2 0.000
#> 2nd-C88_S84 1 0.000
#> 2nd-C8_S14 1 0.747
#> 2nd-C93_S88 1 0.000
#> 2nd-C94_S96 2 0.249
#> 2nd-C95_S95 3 1.000
#> 3rd-C11_S58 1 0.751
#> 3rd-C12_S68 1 0.000
#> 3rd-C18_S80 3 1.000
#> 3rd-C1_S39 1 1.000
#> 3rd-C20_S22 1 0.747
#> 3rd-C21_S11 1 0.000
#> 3rd-C23_S94 2 0.000
#> 3rd-C25_S15 3 1.000
#> 3rd-C26_S28 1 1.000
#> 3rd-C27_S49 3 1.000
#> 3rd-C32_S31 2 0.000
#> 3rd-C33_S50 1 0.000
#> 3rd-C35_S23 3 0.000
#> 3rd-C36_S2 1 0.000
#> 3rd-C3_S2 2 0.000
#> 3rd-C40_S57 3 0.249
#> 3rd-C42_S74 1 1.000
#> 3rd-C44_S32 2 0.498
#> 3rd-C46_S93 1 0.498
#> 3rd-C47_S35 1 0.502
#> 3rd-C49_S60 1 0.747
#> 3rd-C4_S25 1 0.498
#> 3rd-C51_S87 2 0.000
#> 3rd-C52_S86 2 0.000
#> 3rd-C53_S67 1 0.253
#> 3rd-C56_S90 2 0.000
#> 3rd-C57_S5 1 0.000
#> 3rd-C58_S3 1 0.000
#> 3rd-C59_S91 1 0.249
#> 3rd-C60_S10 2 0.000
#> 3rd-C61_S64 2 0.000
#> 3rd-C63_S54 2 0.000
#> 3rd-C65_S20 3 1.000
#> 3rd-C67_S69 1 0.249
#> 3rd-C68_S13 1 0.751
#> 3rd-C69_S78 2 0.000
#> 3rd-C6_S44 3 0.502
#> 3rd-C71_S80 1 0.000
#> 3rd-C76_S22 1 0.000
#> 3rd-C79_S67 1 0.249
#> 3rd-C7_S40 2 0.249
#> 3rd-C82_S11 1 0.000
#> 3rd-C84_S75 1 0.000
#> 3rd-C85_S79 1 0.000
#> 3rd-C85_S83 2 0.000
#> 3rd-C86_S85 3 0.502
#> 3rd-C87_S88 3 0.751
#> 3rd-C88_S24 1 0.249
#> 3rd-C91_S91 1 0.000
#> 3rd-C92_S86 1 0.000
#> 3rd-C95_S81 1 0.000
#> 3rd-C96_S79 3 1.000
#> 3rd-C9_S5 3 1.000
#> 4th-61_S28 1 0.000
#> 4th-C12_S19 1 0.000
#> 4th-C14_S26 1 0.000
#> 4th-C18_S31 3 1.000
#> 4th-C22_S45 3 0.498
#> 4th-C23_S44 3 0.000
#> 4th-C24_S43 1 0.253
#> 4th-C26_S50 1 0.000
#> 4th-C27_S51 2 1.000
#> 4th-C28_S55 1 0.000
#> 4th-C29_S56 1 0.253
#> 4th-C32_S62 1 0.498
#> 4th-C33_S63 1 0.249
#> 4th-C35_S68 2 0.000
#> 4th-C36_S69 3 0.249
#> 4th-C37_S73 3 0.000
#> 4th-C3_S1 2 0.000
#> 4th-C40_S79 1 0.249
#> 4th-C43_S85 1 1.000
#> 4th-C45_S87 2 0.000
#> 4th-C49_S4 1 0.000
#> 4th-C4_S9 1 0.000
#> 4th-C50_S5 2 0.000
#> 4th-C51_S6 1 1.000
#> 4th-C56_S17 3 0.000
#> 4th-C57_S18 2 0.502
#> 4th-C59_S23 1 0.000
#> 4th-C5_S8 1 1.000
#> 4th-C62_S29 1 0.000
#> 4th-C63_S30 1 0.498
#> 4th-C64_S34 1 0.000
#> 4th-C66_S36 1 1.000
#> 4th-C67_S40 3 1.000
#> 4th-C68_S41 3 0.249
#> 4th-C69_S42 1 1.000
#> 4th-C70_S46 1 1.000
#> 4th-C73_S54 1 0.000
#> 4th-C75_S52 1 0.000
#> 4th-C78_S58 1 1.000
#> 4th-C79_S66 3 0.502
#> 4th-C7_S15 1 0.253
#> 4th-C80_S65 1 0.000
#> 4th-C81_S64 3 0.000
#> 4th-C82_S72 1 0.253
#> 4th-C83_S71 3 1.000
#> 4th-C85_S78 1 0.502
#> 4th-C86_S77 1 0.751
#> 4th-C87_S76 1 0.000
#> 4th-C88_S84 1 1.000
#> 4th-C89_S83 1 0.751
#> 4th-C8_S14 1 0.000
#> 4th-C92_S89 1 0.751
#> 4th-C93_S88 3 0.249
#> 4th-C94_S96 3 0.000
#> 4th-C95_S95 3 0.000
#> 4th-C96_S94 1 0.751
#> 4th-C9_S13 2 1.000
#> 5th-C10_S92 2 0.498
#> 5th-C11_S91 2 0.502
#> 5th-C12_S90 3 0.000
#> 5th-C14_S97 2 0.000
#> 5th-C16_S98 3 0.249
#> 5th-C18_S96 2 0.000
#> 5th-C19_S104 3 0.000
#> 5th-C21_S102 1 0.249
#> 5th-C25_S108 2 0.253
#> 5th-C30_S105 1 1.000
#> 5th-C34_S108 1 0.253
#> 5th-C35_S109 3 1.000
#> 5th-C40_S112 2 0.249
#> 5th-C41_S113 3 0.000
#> 5th-C42_S114 2 0.000
#> 5th-C43_S121 3 0.000
#> 5th-C45_S123 2 0.498
#> 5th-C47_S118 3 0.000
#> 5th-C49_S89 1 0.249
#> 5th-C50_S90 3 0.000
#> 5th-C54_S89 3 0.000
#> 5th-C56_S95 2 0.249
#> 5th-C57_S96 1 1.000
#> 5th-C58_S93 2 0.751
#> 5th-C59_S94 1 0.502
#> 5th-C5_S85 1 0.000
#> 5th-C64_S99 1 0.000
#> 5th-C66_S101 1 0.000
#> 5th-C67_S105 2 0.502
#> 5th-C68_S106 1 0.000
#> 5th-C69_S107 1 0.000
#> 5th-C6_S84 2 0.249
#> 5th-C70_S103 2 0.000
#> 5th-C73_S111 2 0.498
#> 5th-C74_S110 1 0.000
#> 5th-C77_S107 3 0.000
#> 5th-C7_S93 1 0.502
#> 5th-C80_S116 3 1.000
#> 5th-C81_S115 3 0.751
#> 5th-C83_S111 2 0.000
#> 5th-C87_S119 2 0.249
#> 5th-C88_S117 2 0.000
#> 5th-C90_S115 3 0.502
#> 5th-C92_S124 1 0.751
#> 5th-C9_S92 1 0.502
#> 6th-C12_S18 1 0.000
#> 6th-C15_S22 2 0.000
#> 6th-C16_S29 1 0.000
#> 6th-C19_S35 3 1.000
#> 6th-C1_S3 2 0.000
#> 6th-C20_S34 3 1.000
#> 6th-C21_S33 1 0.249
#> 6th-C22_S39 3 0.000
#> 6th-C23_S38 1 0.000
#> 6th-C24_S37 1 0.253
#> 6th-C25_S43 3 0.502
#> 6th-C28_S49 2 0.000
#> 6th-C29_S50 1 0.000
#> 6th-C2_S2 3 1.000
#> 6th-C30_S51 3 1.000
#> 6th-C34_S61 2 0.249
#> 6th-C40_S73 3 0.498
#> 6th-C42_S75 3 0.751
#> 6th-C45_S81 2 0.253
#> 6th-C51_S6 3 1.000
#> 6th-C53_S10 1 1.000
#> 6th-C54_S11 1 0.000
#> 6th-C57_S17 2 0.000
#> 6th-C58_S20 2 0.253
#> 6th-C59_S21 1 0.000
#> 6th-C5_S8 1 0.502
#> 6th-C62_S25 2 0.000
#> 6th-C63_S26 1 0.000
#> 6th-C64_S30 2 0.000
#> 6th-C65_S31 1 0.249
#> 6th-C66_S32 1 0.498
#> 6th-C67_S36 3 1.000
#> 6th-C71_S41 1 0.000
#> 6th-C73_S48 3 1.000
#> 6th-C75_S46 3 1.000
#> 6th-C77_S53 1 0.000
#> 6th-C79_S60 1 0.000
#> 6th-C80_S59 1 0.498
#> 6th-C82_S66 2 0.000
#> 6th-C83_S65 2 0.000
#> 6th-C84_S64 2 0.000
#> 6th-C85_S72 1 0.000
#> 6th-C87_S70 1 0.000
#> 6th-C89_S77 2 0.000
#> 6th-C90_S76 2 0.000
#> 6th-C91_S84 3 1.000
#> 6th-C93_S82 1 0.253
#> 6th-C9_S12 2 0.000
#> 7th-C10_S19 3 1.000
#> 7th-C11_S18 3 1.000
#> 7th-C12_S17 2 0.000
#> 7th-C14_S24 1 0.502
#> 7th-C15_S23 3 1.000
#> 7th-C17_S29 1 1.000
#> 7th-C19_S36 2 0.249
#> 7th-C1_S3 2 0.000
#> 7th-C20_S35 2 0.000
#> 7th-C21_S34 2 0.000
#> 7th-C24_S40 1 0.000
#> 7th-C25_S43 1 0.000
#> 7th-C28_S48 3 1.000
#> 7th-C2_S2 2 0.000
#> 7th-C31_S53 3 1.000
#> 7th-C32_S54 1 0.502
#> 7th-C34_S59 1 0.000
#> 7th-C36_S61 3 0.249
#> 7th-C3_S1 2 0.000
#> 7th-C40_S70 3 0.000
#> 7th-C44_S76 3 0.000
#> 7th-C45_S77 1 0.000
#> 7th-C47_S81 2 1.000
#> 7th-C49_S4 2 0.000
#> 7th-C4_S8 2 0.000
#> 7th-C50_S5 1 0.000
#> 7th-C52_S9 2 0.000
#> 7th-C53_S10 1 0.000
#> 7th-C56_S15 3 0.000
#> 7th-C57_S16 2 0.000
#> 7th-C58_S20 1 0.000
#> 7th-C59_S21 1 0.000
#> 7th-C60_S22 2 0.000
#> 7th-C62_S27 1 0.249
#> 7th-C64_S31 1 0.000
#> 7th-C65_S32 2 0.000
#> 7th-C66_S33 1 0.000
#> 7th-C68_S38 1 0.000
#> 7th-C69_S39 3 1.000
#> 7th-C72_S42 1 0.751
#> 7th-C73_S47 3 0.502
#> 7th-C76_S52 2 0.751
#> 7th-C77_S51 1 0.000
#> 7th-C79_S58 3 1.000
#> 7th-C80_S57 3 1.000
#> 7th-C81_S56 2 0.751
#> 7th-C82_S64 1 0.000
#> 7th-C84_S62 1 0.000
#> 7th-C85_S69 2 0.000
#> 7th-C88_S75 1 1.000
#> 7th-C89_S74 3 1.000
#> 7th-C8_S13 1 0.000
#> 7th-C90_S73 1 0.000
#> 7th-C94_S83 2 0.000
#> 7th-C96_S82 1 0.000
#> 8th-C10_S100 1 0.249
#> 8th-C11_S99 1 0.502
#> 8th-C18_S110 2 1.000
#> 8th-C20_S116 1 0.751
#> 8th-C21_S115 2 0.249
#> 8th-C23_S121 2 0.000
#> 8th-C24_S120 1 0.751
#> 8th-C26_S126 2 0.000
#> 8th-C28_S131 2 0.751
#> 8th-C2_S85 1 0.000
#> 8th-C34_S141 1 0.249
#> 8th-C37_S146 2 0.249
#> 8th-C38_S147 2 0.000
#> 8th-C44_S155 3 1.000
#> 8th-C47_S160 2 0.000
#> 8th-C55_S96 1 0.502
#> 8th-C57_S98 3 0.751
#> 8th-C58_S101 1 0.000
#> 8th-C59_S102 1 0.253
#> 8th-C61_S107 1 0.249
#> 8th-C64_S112 1 0.751
#> 8th-C65_S113 1 0.253
#> 8th-C67_S117 1 1.000
#> 8th-C69_S119 2 0.498
#> 8th-C6_S88 1 0.000
#> 8th-C70_S123 2 0.000
#> 8th-C73_S130 1 1.000
#> 8th-C74_S129 1 0.249
#> 8th-C75_S128 2 0.000
#> 8th-C79_S140 2 0.000
#> 8th-C7_S95 3 0.751
#> 8th-C84_S143 2 0.249
#> 8th-C85_S150 1 1.000
#> 8th-C87_S148 1 0.000
#> 8th-C90_S152 2 0.000
#> 8th-C91_S158 2 1.000
#> 8th-C92_S157 1 0.751
#> 8th-C94_S162 2 0.000
#> 8th-C95_S161 3 0.000
#> 9th-C10_S18 3 1.000
#> 9th-C11_S17 3 0.000
#> 9th-C13_S24 2 0.000
#> 9th-C14_S23 2 0.249
#> 9th-C15_S22 1 0.000
#> 9th-C16_S30 3 0.000
#> 9th-C17_S29 3 0.000
#> 9th-C19_S36 1 1.000
#> 9th-C1_S3 3 1.000
#> 9th-C20_S35 2 1.000
#> 9th-C22_S41 2 1.000
#> 9th-C25_S45 2 0.000
#> 9th-C28_S50 1 1.000
#> 9th-C29_S51 1 1.000
#> 9th-C2_S2 2 0.502
#> 9th-C30_S52 1 0.249
#> 9th-C36_S59 1 1.000
#> 9th-C38_S64 3 0.498
#> 9th-C3_S1 3 0.751
#> 9th-C40_S69 3 0.000
#> 9th-C41_S70 1 0.249
#> 9th-C46_S79 3 1.000
#> 9th-C49_S4 2 0.000
#> 9th-C51_S6 2 0.249
#> 9th-C52_S10 2 0.000
#> 9th-C57_S16 3 1.000
#> 9th-C59_S20 2 0.000
#> 9th-C5_S8 1 1.000
#> 9th-C61_S25 3 0.000
#> 9th-C62_S26 1 0.249
#> 9th-C64_S31 1 0.000
#> 9th-C65_S32 3 1.000
#> 9th-C66_S33 3 0.000
#> 9th-C67_S37 3 0.000
#> 9th-C69_S39 3 0.502
#> 9th-C6_S7 1 0.249
#> 9th-C70_S42 1 0.249
#> 9th-C74_S48 1 0.000
#> 9th-C75_S47 2 0.249
#> 9th-C77_S53 1 0.253
#> 9th-C79_S57 2 0.249
#> 9th-C80_S56 3 0.000
#> 9th-C81_S55 3 1.000
#> 9th-C83_S61 1 0.502
#> 9th-C84_S60 1 0.751
#> 9th-C85_S68 2 0.000
#> 9th-C86_S67 1 0.253
#> 9th-C87_S66 2 0.000
#> 9th-C88_S73 2 0.000
#> 9th-C89_S72 1 0.751
#> 9th-C8_S14 1 1.000
#> 9th-C91_S78 3 0.000
#> 9th-C92_S77 2 0.498
#> 9th-C93_S76 3 0.502
#> 9th-C94_S83 2 0.000
#> 9th-C96_S81 1 1.000
#> 9th-C9_S13 3 0.000
get_classes(res, k = 4)
#> class p
#> 10th_C10_S104 3 0.000
#> 10th_C11_S96 2 0.253
#> 10th_C13_S61 1 0.000
#> 10th_C14_S53 1 0.249
#> 10th_C16_S105 1 0.000
#> 10th_C17_S97 2 0.000
#> 10th_C19_S62 3 0.000
#> 10th_C1_S59 1 0.000
#> 10th_C20_S54 1 0.000
#> 10th_C23_S98 3 0.000
#> 10th_C24_S90 3 1.000
#> 10th_C28_S91 4 0.253
#> 10th_C30_S107 1 0.747
#> 10th_C31_S48 3 0.253
#> 10th_C32_S56 2 0.502
#> 10th_C33_S64 2 0.000
#> 10th_C34_S92 4 1.000
#> 10th_C37_S49 2 1.000
#> 10th_C41_S101 3 0.000
#> 10th_C42_S109 2 0.000
#> 10th_C43_S50 2 0.249
#> 10th_C45_S66 3 0.000
#> 10th_C46_S94 3 1.000
#> 10th_C4_S103 3 0.000
#> 10th_C50_S73 2 1.000
#> 10th_C51_S80 2 0.249
#> 10th_C52_S110 2 0.253
#> 10th_C53_S118 2 0.000
#> 10th_C54_S124 1 1.000
#> 10th_C56_S74 1 1.000
#> 10th_C57_S81 2 0.249
#> 10th_C58_S111 4 0.253
#> 10th_C5_S95 2 0.000
#> 10th_C61_S68 2 0.498
#> 10th_C63_S82 2 0.253
#> 10th_C64_S112 2 0.502
#> 10th_C66_S126 2 0.000
#> 10th_C68_S75 3 0.000
#> 10th_C6_S88 4 0.000
#> 10th_C73_S84 3 1.000
#> 10th_C74_S76 1 0.249
#> 10th_C76_S128 1 0.498
#> 10th_C77_S120 2 0.000
#> 10th_C78_S114 2 0.498
#> 10th_C7_S60 1 1.000
#> 10th_C80_S77 2 0.000
#> 10th_C81_S70 4 0.751
#> 10th_C84_S115 1 0.000
#> 10th_C85_S86 3 0.751
#> 10th_C86_S78 2 0.000
#> 10th_C87_S71 2 0.000
#> 10th_C88_S130 3 0.000
#> 10th_C8_S52 4 1.000
#> 10th_C90_S116 1 0.000
#> 10th_C95_S123 2 0.000
#> 10th_C96_S117 4 0.747
#> 11th-C10_S63 2 0.000
#> 11th-C12_S47 4 0.502
#> 11th-C16_S64 1 1.000
#> 11th-C21_S4 2 1.000
#> 11th-C22_S65 2 0.498
#> 11th-C24_S49 3 0.000
#> 11th-C26_S12 2 0.253
#> 11th-C27_S19 2 0.000
#> 11th-C2_S8 2 0.000
#> 11th-C30_S66 2 0.249
#> 11th-C33_S20 3 0.000
#> 11th-C36_S67 1 0.249
#> 11th-C37_S6 2 0.000
#> 11th-C39_S21 1 0.000
#> 11th-C40_S52 3 0.498
#> 11th-C41_S60 1 0.000
#> 11th-C43_S7 4 1.000
#> 11th-C44_S15 4 0.000
#> 11th-C49_S23 3 1.000
#> 11th-C4_S62 3 1.000
#> 11th-C51_S39 4 0.000
#> 11th-C53_S78 1 0.000
#> 11th-C54_S86 4 0.498
#> 11th-C55_S24 2 0.000
#> 11th-C56_S32 2 0.000
#> 11th-C57_S40 2 0.000
#> 11th-C58_S71 1 1.000
#> 11th-C5_S54 3 1.000
#> 11th-C61_S25 1 0.249
#> 11th-C62_S33 4 1.000
#> 11th-C64_S72 3 1.000
#> 11th-C66_S88 1 0.000
#> 11th-C67_S26 2 0.000
#> 11th-C68_S34 3 0.000
#> 11th-C77_S82 2 0.000
#> 11th-C7_S16 3 0.000
#> 11th-C93_S30 2 0.000
#> 12th-C10_S155 2 0.751
#> 12th-C11_S147 4 0.000
#> 12th-C12_S139 4 0.000
#> 12th-C14_S190 1 1.000
#> 12th-C15_S183 2 0.000
#> 12th-C1_S195 2 0.000
#> 12th-C20_S191 1 1.000
#> 12th-C21_S184 2 0.000
#> 12th-C23_S149 2 0.000
#> 12th-C24_S141 4 0.751
#> 12th-C25_S185 3 1.000
#> 12th-C26_S192 4 0.000
#> 12th-C28_S142 1 0.253
#> 12th-C29_S150 1 0.000
#> 12th-C30_S157 1 0.000
#> 12th-C33_S200 4 0.000
#> 12th-C35_S151 2 1.000
#> 12th-C36_S158 2 0.249
#> 12th-C37_S187 4 1.000
#> 12th-C38_S194 2 0.498
#> 12th-C39_S201 2 0.000
#> 12th-C3_S181 2 0.000
#> 12th-C40_S144 2 0.000
#> 12th-C42_S159 4 0.000
#> 12th-C46_S145 1 1.000
#> 12th-C47_S153 2 0.253
#> 12th-C48_S160 1 0.253
#> 12th-C4_S154 2 0.000
#> 12th-C50_S210 2 1.000
#> 12th-C51_S217 4 0.000
#> 12th-C53_S168 4 1.000
#> 12th-C55_S203 4 0.000
#> 12th-C56_S211 3 1.000
#> 12th-C57_S218 2 0.000
#> 12th-C58_S162 1 0.000
#> 12th-C59_S169 1 0.000
#> 12th-C60_S176 1 0.000
#> 12th-C63_S219 4 1.000
#> 12th-C64_S163 1 0.000
#> 12th-C65_S170 4 0.000
#> 12th-C67_S205 4 0.249
#> 12th-C69_S135 3 0.000
#> 12th-C71_S171 2 0.751
#> 12th-C74_S214 1 0.249
#> 12th-C75_S206 2 0.249
#> 12th-C76_S177 1 0.751
#> 12th-C7_S196 4 0.000
#> 12th-C80_S215 3 0.000
#> 12th-C81_S207 4 0.751
#> 12th-C84_S165 1 0.000
#> 12th-C85_S137 4 0.249
#> 12th-C8_S189 2 0.751
#> 12th-C90_S166 1 0.751
#> 12th-C93_S209 2 0.751
#> 12th-C94_S180 3 0.000
#> 12th-C95_S174 1 0.000
#> 12th-C96_S167 1 0.000
#> 13th_C12_S178 3 0.498
#> 13th_C13_S149 3 0.000
#> 13th_C15_S134 4 0.000
#> 13th_C16_S193 4 0.498
#> 13th_C17_S186 4 0.000
#> 13th_C18_S179 2 0.000
#> 13th_C1_S147 2 0.000
#> 13th_C20_S142 2 0.000
#> 13th_C21_S135 2 0.000
#> 13th_C23_S187 3 1.000
#> 13th_C27_S151 2 0.000
#> 13th_C29_S188 2 0.000
#> 13th_C31_S137 4 1.000
#> 13th_C34_S181 4 0.000
#> 13th_C36_S196 4 0.249
#> 13th_C38_S145 2 0.751
#> 13th_C39_S153 3 0.498
#> 13th_C3_S132 2 0.000
#> 13th_C46_S183 2 0.502
#> 13th_C49_S155 2 0.000
#> 13th_C4_S191 2 0.000
#> 13th_C51_S170 2 1.000
#> 13th_C52_S198 2 1.000
#> 13th_C53_S205 2 0.000
#> 13th_C54_S212 2 0.000
#> 13th_C55_S156 4 0.249
#> 13th_C57_S171 2 0.000
#> 13th_C5_S184 4 0.000
#> 13th_C60_S213 3 0.000
#> 13th_C63_S172 4 0.249
#> 13th_C66_S214 1 0.502
#> 13th_C68_S165 2 0.502
#> 13th_C69_S173 2 0.000
#> 13th_C6_S177 2 0.249
#> 13th_C70_S201 4 0.000
#> 13th_C71_S208 4 0.000
#> 13th_C72_S215 4 0.747
#> 13th_C75_S159 2 1.000
#> 13th_C76_S216 4 0.751
#> 13th_C77_S209 2 0.000
#> 13th_C79_S174 4 0.502
#> 13th_C80_S167 4 0.000
#> 13th_C81_S160 4 0.000
#> 13th_C86_S168 2 0.249
#> 13th_C88_S218 4 1.000
#> 13th_C89_S211 2 0.498
#> 13th_C8_S140 2 0.249
#> 13th_C92_S169 2 0.502
#> 13th_C93_S162 2 0.000
#> 13th_C94_S219 4 0.000
#> 13th_C96_S204 4 0.000
#> 1st-61_S27 1 0.751
#> 1st-C11_S58 1 0.249
#> 1st-C13_S19 2 0.253
#> 1st-C15_S3 2 0.000
#> 1st-C18_S51 2 0.000
#> 1st-C19_S20 3 0.498
#> 1st-C20_S12 2 0.000
#> 1st-C21_S4 3 0.000
#> 1st-C32_S14 4 0.000
#> 1st-C34_S54 1 1.000
#> 1st-C39_S23 2 0.000
#> 1st-C42_S71 1 1.000
#> 1st-C50_S33 1 0.498
#> 1st-C51_S41 2 0.253
#> 1st-C53_S74 2 0.751
#> 1st-C56_S34 1 0.000
#> 1st-C57_S42 1 1.000
#> 1st-C58_S76 1 1.000
#> 1st-C59_S77 4 0.249
#> 1st-C62_S35 2 0.502
#> 1st-C64_S79 1 0.502
#> 1st-C68_S36 1 1.000
#> 1st-C69_S44 1 1.000
#> 1st-C71_S83 3 1.000
#> 1st-C73_S45 1 1.000
#> 1st-C74_S37 4 0.000
#> 1st-C75_S29 1 0.249
#> 1st-C77_S86 3 1.000
#> 1st-C78_S85 3 0.502
#> 1st-C79_S46 2 0.253
#> 1st-C80_S38 1 0.000
#> 1st-C8_S10 2 0.498
#> 1st-C90_S91 1 0.000
#> 1st-C96_S94 2 0.502
#> 2nd-C11_S20 1 0.249
#> 2nd-C15_S25 1 0.000
#> 2nd-C16_S33 1 0.000
#> 2nd-C17_S32 1 0.253
#> 2nd-C19_S39 2 0.249
#> 2nd-C1_S3 2 0.000
#> 2nd-C21_S37 3 1.000
#> 2nd-C25_S49 1 0.502
#> 2nd-C26_S50 1 0.000
#> 2nd-C27_S51 2 0.751
#> 2nd-C28_S55 4 0.751
#> 2nd-C29_S56 1 0.000
#> 2nd-C2_S2 2 0.000
#> 2nd-C31_S61 1 0.498
#> 2nd-C32_S62 1 0.000
#> 2nd-C36_S69 4 1.000
#> 2nd-C37_S73 2 0.249
#> 2nd-C38_S74 1 0.000
#> 2nd-C39_S75 1 0.000
#> 2nd-C3_S1 2 0.000
#> 2nd-C47_S92 1 0.253
#> 2nd-C49_S4 2 1.000
#> 2nd-C4_S9 2 0.000
#> 2nd-C51_S6 2 0.751
#> 2nd-C52_S10 2 0.751
#> 2nd-C54_S12 1 1.000
#> 2nd-C57_S18 1 0.751
#> 2nd-C58_S22 4 0.249
#> 2nd-C5_S8 2 1.000
#> 2nd-C62_S29 1 0.000
#> 2nd-C67_S40 1 0.502
#> 2nd-C69_S42 4 1.000
#> 2nd-C6_S7 3 0.502
#> 2nd-C72_S48 1 0.000
#> 2nd-C74_S53 1 0.000
#> 2nd-C75_S52 1 0.751
#> 2nd-C76_S60 1 0.249
#> 2nd-C77_S59 4 0.000
#> 2nd-C7_S15 2 1.000
#> 2nd-C80_S65 1 0.000
#> 2nd-C81_S64 4 0.000
#> 2nd-C83_S71 3 0.249
#> 2nd-C86_S77 4 0.000
#> 2nd-C87_S76 2 0.000
#> 2nd-C88_S84 1 0.000
#> 2nd-C8_S14 1 0.498
#> 2nd-C93_S88 1 0.000
#> 2nd-C94_S96 2 0.000
#> 2nd-C95_S95 4 0.249
#> 3rd-C11_S58 1 1.000
#> 3rd-C12_S68 1 0.000
#> 3rd-C18_S80 3 0.249
#> 3rd-C1_S39 1 0.249
#> 3rd-C20_S22 1 0.502
#> 3rd-C21_S11 1 0.000
#> 3rd-C23_S94 2 0.751
#> 3rd-C25_S15 4 0.000
#> 3rd-C26_S28 1 0.249
#> 3rd-C27_S49 3 0.249
#> 3rd-C32_S31 2 0.498
#> 3rd-C33_S50 1 0.000
#> 3rd-C35_S23 3 0.751
#> 3rd-C36_S2 1 0.000
#> 3rd-C3_S2 2 0.751
#> 3rd-C40_S57 3 0.000
#> 3rd-C42_S74 1 0.751
#> 3rd-C44_S32 2 0.751
#> 3rd-C46_S93 1 0.000
#> 3rd-C47_S35 1 0.502
#> 3rd-C49_S60 1 0.000
#> 3rd-C4_S25 1 0.000
#> 3rd-C51_S87 2 0.502
#> 3rd-C52_S86 2 0.000
#> 3rd-C53_S67 1 0.253
#> 3rd-C56_S90 2 1.000
#> 3rd-C57_S5 1 0.000
#> 3rd-C58_S3 1 0.249
#> 3rd-C59_S91 1 0.249
#> 3rd-C60_S10 2 0.000
#> 3rd-C61_S64 4 0.249
#> 3rd-C63_S54 2 0.000
#> 3rd-C65_S20 4 0.000
#> 3rd-C67_S69 1 0.000
#> 3rd-C68_S13 1 0.000
#> 3rd-C69_S78 2 0.498
#> 3rd-C6_S44 4 0.751
#> 3rd-C71_S80 1 0.249
#> 3rd-C76_S22 1 0.249
#> 3rd-C79_S67 1 0.249
#> 3rd-C7_S40 2 0.000
#> 3rd-C82_S11 1 0.000
#> 3rd-C84_S75 1 0.000
#> 3rd-C85_S79 1 0.498
#> 3rd-C85_S83 2 0.000
#> 3rd-C86_S85 4 0.498
#> 3rd-C87_S88 4 0.747
#> 3rd-C88_S24 1 0.000
#> 3rd-C91_S91 1 0.000
#> 3rd-C92_S86 1 0.000
#> 3rd-C95_S81 1 0.000
#> 3rd-C96_S79 4 0.000
#> 3rd-C9_S5 4 0.498
#> 4th-61_S28 1 0.000
#> 4th-C12_S19 1 0.000
#> 4th-C14_S26 1 0.000
#> 4th-C18_S31 3 1.000
#> 4th-C22_S45 4 0.747
#> 4th-C23_S44 3 0.498
#> 4th-C24_S43 1 0.000
#> 4th-C26_S50 1 0.502
#> 4th-C27_S51 4 1.000
#> 4th-C28_S55 1 0.000
#> 4th-C29_S56 1 0.747
#> 4th-C32_S62 1 0.000
#> 4th-C33_S63 1 0.751
#> 4th-C35_S68 2 0.000
#> 4th-C36_S69 4 0.249
#> 4th-C37_S73 4 0.498
#> 4th-C3_S1 2 0.498
#> 4th-C40_S79 1 0.000
#> 4th-C43_S85 1 0.249
#> 4th-C45_S87 2 0.253
#> 4th-C49_S4 1 0.000
#> 4th-C4_S9 1 0.000
#> 4th-C50_S5 2 0.249
#> 4th-C51_S6 1 0.253
#> 4th-C56_S17 3 0.000
#> 4th-C57_S18 2 0.253
#> 4th-C59_S23 1 0.000
#> 4th-C5_S8 1 0.498
#> 4th-C62_S29 1 0.000
#> 4th-C63_S30 1 0.751
#> 4th-C64_S34 1 0.000
#> 4th-C66_S36 1 0.000
#> 4th-C67_S40 3 0.751
#> 4th-C68_S41 4 1.000
#> 4th-C69_S42 1 0.000
#> 4th-C70_S46 1 0.502
#> 4th-C73_S54 1 0.000
#> 4th-C75_S52 1 0.000
#> 4th-C78_S58 1 1.000
#> 4th-C79_S66 3 0.502
#> 4th-C7_S15 1 0.000
#> 4th-C80_S65 1 0.000
#> 4th-C81_S64 3 0.000
#> 4th-C82_S72 1 0.000
#> 4th-C83_S71 4 0.747
#> 4th-C85_S78 1 0.000
#> 4th-C86_S77 1 0.000
#> 4th-C87_S76 1 0.249
#> 4th-C88_S84 1 0.253
#> 4th-C89_S83 1 0.249
#> 4th-C8_S14 1 0.000
#> 4th-C92_S89 1 0.249
#> 4th-C93_S88 4 0.000
#> 4th-C94_S96 3 0.000
#> 4th-C95_S95 3 0.498
#> 4th-C96_S94 1 0.502
#> 4th-C9_S13 4 0.000
#> 5th-C10_S92 2 0.000
#> 5th-C11_S91 2 0.000
#> 5th-C12_S90 3 0.000
#> 5th-C14_S97 2 0.253
#> 5th-C16_S98 4 0.747
#> 5th-C18_S96 2 0.498
#> 5th-C19_S104 3 0.000
#> 5th-C21_S102 1 0.000
#> 5th-C25_S108 2 0.000
#> 5th-C30_S105 1 1.000
#> 5th-C34_S108 1 0.502
#> 5th-C35_S109 4 1.000
#> 5th-C40_S112 2 0.000
#> 5th-C41_S113 3 1.000
#> 5th-C42_S114 2 0.000
#> 5th-C43_S121 3 0.000
#> 5th-C45_S123 2 0.000
#> 5th-C47_S118 3 0.000
#> 5th-C49_S89 1 0.253
#> 5th-C50_S90 3 0.000
#> 5th-C54_S89 3 0.000
#> 5th-C56_S95 2 0.249
#> 5th-C57_S96 1 0.498
#> 5th-C58_S93 2 0.249
#> 5th-C59_S94 1 0.498
#> 5th-C5_S85 1 0.000
#> 5th-C64_S99 1 0.000
#> 5th-C66_S101 1 0.000
#> 5th-C67_S105 2 0.000
#> 5th-C68_S106 1 0.000
#> 5th-C69_S107 1 0.000
#> 5th-C6_S84 2 0.502
#> 5th-C70_S103 4 0.000
#> 5th-C73_S111 2 0.249
#> 5th-C74_S110 1 0.000
#> 5th-C77_S107 3 0.253
#> 5th-C7_S93 1 0.249
#> 5th-C80_S116 4 0.000
#> 5th-C81_S115 4 0.000
#> 5th-C83_S111 2 0.000
#> 5th-C87_S119 2 1.000
#> 5th-C88_S117 2 0.000
#> 5th-C90_S115 4 0.000
#> 5th-C92_S124 1 0.502
#> 5th-C9_S92 1 0.502
#> 6th-C12_S18 1 0.000
#> 6th-C15_S22 2 0.000
#> 6th-C16_S29 1 0.000
#> 6th-C19_S35 4 0.000
#> 6th-C1_S3 2 0.000
#> 6th-C20_S34 4 0.000
#> 6th-C21_S33 1 0.000
#> 6th-C22_S39 4 0.498
#> 6th-C23_S38 1 0.249
#> 6th-C24_S37 1 0.249
#> 6th-C25_S43 4 0.000
#> 6th-C28_S49 4 1.000
#> 6th-C29_S50 1 0.000
#> 6th-C2_S2 3 1.000
#> 6th-C30_S51 4 0.000
#> 6th-C34_S61 2 0.000
#> 6th-C40_S73 3 0.249
#> 6th-C42_S75 4 1.000
#> 6th-C45_S81 2 0.000
#> 6th-C51_S6 4 0.000
#> 6th-C53_S10 1 1.000
#> 6th-C54_S11 1 0.000
#> 6th-C57_S17 2 0.249
#> 6th-C58_S20 2 0.249
#> 6th-C59_S21 1 0.000
#> 6th-C5_S8 1 0.253
#> 6th-C62_S25 2 0.253
#> 6th-C63_S26 1 0.000
#> 6th-C64_S30 2 0.751
#> 6th-C65_S31 1 0.249
#> 6th-C66_S32 1 0.253
#> 6th-C67_S36 4 0.502
#> 6th-C71_S41 1 0.000
#> 6th-C73_S48 4 0.000
#> 6th-C75_S46 4 0.000
#> 6th-C77_S53 1 0.000
#> 6th-C79_S60 1 0.249
#> 6th-C80_S59 1 0.000
#> 6th-C82_S66 2 0.000
#> 6th-C83_S65 4 0.747
#> 6th-C84_S64 2 0.000
#> 6th-C85_S72 1 0.000
#> 6th-C87_S70 1 0.000
#> 6th-C89_S77 2 0.000
#> 6th-C90_S76 2 1.000
#> 6th-C91_S84 3 0.000
#> 6th-C93_S82 1 0.249
#> 6th-C9_S12 2 0.000
#> 7th-C10_S19 4 0.000
#> 7th-C11_S18 3 0.249
#> 7th-C12_S17 2 0.249
#> 7th-C14_S24 1 1.000
#> 7th-C15_S23 4 0.000
#> 7th-C17_S29 1 0.751
#> 7th-C19_S36 2 0.000
#> 7th-C1_S3 2 0.000
#> 7th-C20_S35 2 0.249
#> 7th-C21_S34 2 0.253
#> 7th-C24_S40 1 0.000
#> 7th-C25_S43 1 0.000
#> 7th-C28_S48 4 0.000
#> 7th-C2_S2 2 1.000
#> 7th-C31_S53 4 0.000
#> 7th-C32_S54 1 0.502
#> 7th-C34_S59 1 0.253
#> 7th-C36_S61 1 0.747
#> 7th-C3_S1 2 0.249
#> 7th-C40_S70 3 0.000
#> 7th-C44_S76 3 0.000
#> 7th-C45_S77 1 0.000
#> 7th-C47_S81 3 0.751
#> 7th-C49_S4 2 0.000
#> 7th-C4_S8 2 0.000
#> 7th-C50_S5 1 0.000
#> 7th-C52_S9 2 0.502
#> 7th-C53_S10 1 0.000
#> 7th-C56_S15 3 0.000
#> 7th-C57_S16 2 1.000
#> 7th-C58_S20 1 0.000
#> 7th-C59_S21 1 0.000
#> 7th-C60_S22 2 0.747
#> 7th-C62_S27 1 0.253
#> 7th-C64_S31 1 0.000
#> 7th-C65_S32 2 0.000
#> 7th-C66_S33 1 0.249
#> 7th-C68_S38 1 0.498
#> 7th-C69_S39 4 0.000
#> 7th-C72_S42 1 1.000
#> 7th-C73_S47 4 0.000
#> 7th-C76_S52 2 0.502
#> 7th-C77_S51 1 0.000
#> 7th-C79_S58 4 0.249
#> 7th-C80_S57 4 0.000
#> 7th-C81_S56 2 0.000
#> 7th-C82_S64 1 0.502
#> 7th-C84_S62 1 0.000
#> 7th-C85_S69 2 0.000
#> 7th-C88_S75 1 0.747
#> 7th-C89_S74 4 0.000
#> 7th-C8_S13 1 0.000
#> 7th-C90_S73 1 0.000
#> 7th-C94_S83 2 0.000
#> 7th-C96_S82 1 0.000
#> 8th-C10_S100 1 0.000
#> 8th-C11_S99 1 0.253
#> 8th-C18_S110 2 0.000
#> 8th-C20_S116 1 0.000
#> 8th-C21_S115 2 0.747
#> 8th-C23_S121 2 0.498
#> 8th-C24_S120 1 0.000
#> 8th-C26_S126 2 0.000
#> 8th-C28_S131 2 0.502
#> 8th-C2_S85 1 0.000
#> 8th-C34_S141 1 0.000
#> 8th-C37_S146 2 0.249
#> 8th-C38_S147 2 0.000
#> 8th-C44_S155 3 1.000
#> 8th-C47_S160 2 0.751
#> 8th-C55_S96 1 0.249
#> 8th-C57_S98 4 0.751
#> 8th-C58_S101 1 0.249
#> 8th-C59_S102 1 0.502
#> 8th-C61_S107 1 0.000
#> 8th-C64_S112 1 0.498
#> 8th-C65_S113 1 0.000
#> 8th-C67_S117 1 1.000
#> 8th-C69_S119 2 0.000
#> 8th-C6_S88 1 0.000
#> 8th-C70_S123 2 0.000
#> 8th-C73_S130 1 0.747
#> 8th-C74_S129 1 0.253
#> 8th-C75_S128 2 0.000
#> 8th-C79_S140 2 0.000
#> 8th-C7_S95 1 0.502
#> 8th-C84_S143 2 0.498
#> 8th-C85_S150 1 0.747
#> 8th-C87_S148 1 0.000
#> 8th-C90_S152 2 0.000
#> 8th-C91_S158 2 0.000
#> 8th-C92_S157 1 0.498
#> 8th-C94_S162 2 0.249
#> 8th-C95_S161 3 0.000
#> 9th-C10_S18 3 1.000
#> 9th-C11_S17 3 0.000
#> 9th-C13_S24 2 0.751
#> 9th-C14_S23 2 0.000
#> 9th-C15_S22 1 0.000
#> 9th-C16_S30 3 0.751
#> 9th-C17_S29 3 0.000
#> 9th-C19_S36 1 0.498
#> 9th-C1_S3 4 0.000
#> 9th-C20_S35 4 1.000
#> 9th-C22_S41 2 0.000
#> 9th-C25_S45 2 0.747
#> 9th-C28_S50 1 0.249
#> 9th-C29_S51 1 0.498
#> 9th-C2_S2 2 0.000
#> 9th-C30_S52 1 0.249
#> 9th-C36_S59 1 1.000
#> 9th-C38_S64 3 1.000
#> 9th-C3_S1 3 0.498
#> 9th-C40_S69 3 0.000
#> 9th-C41_S70 1 0.000
#> 9th-C46_S79 4 0.751
#> 9th-C49_S4 2 0.000
#> 9th-C51_S6 2 1.000
#> 9th-C52_S10 2 0.502
#> 9th-C57_S16 3 1.000
#> 9th-C59_S20 2 0.498
#> 9th-C5_S8 1 1.000
#> 9th-C61_S25 3 0.000
#> 9th-C62_S26 1 0.000
#> 9th-C64_S31 1 0.000
#> 9th-C65_S32 3 1.000
#> 9th-C66_S33 3 0.000
#> 9th-C67_S37 3 0.000
#> 9th-C69_S39 4 0.000
#> 9th-C6_S7 1 0.000
#> 9th-C70_S42 1 0.000
#> 9th-C74_S48 1 0.000
#> 9th-C75_S47 2 0.000
#> 9th-C77_S53 1 0.000
#> 9th-C79_S57 2 0.000
#> 9th-C80_S56 3 0.000
#> 9th-C81_S55 4 0.000
#> 9th-C83_S61 1 0.000
#> 9th-C84_S60 1 0.249
#> 9th-C85_S68 2 0.249
#> 9th-C86_S67 1 0.000
#> 9th-C87_S66 2 0.000
#> 9th-C88_S73 2 0.000
#> 9th-C89_S72 1 0.751
#> 9th-C8_S14 1 0.751
#> 9th-C91_S78 4 1.000
#> 9th-C92_S77 2 0.253
#> 9th-C93_S76 4 0.253
#> 9th-C94_S83 2 0.000
#> 9th-C96_S81 1 1.000
#> 9th-C9_S13 3 0.751
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)

consensus_heatmap(res, k = 3)
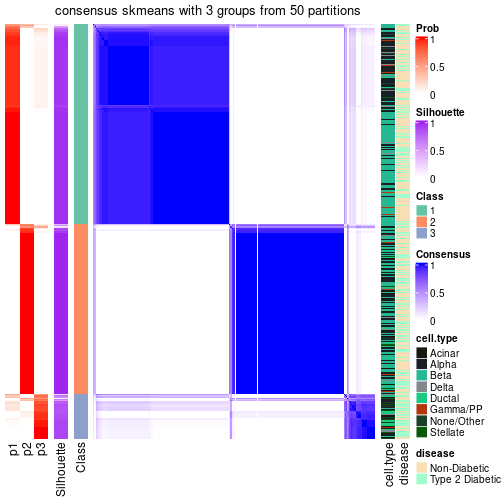
consensus_heatmap(res, k = 4)
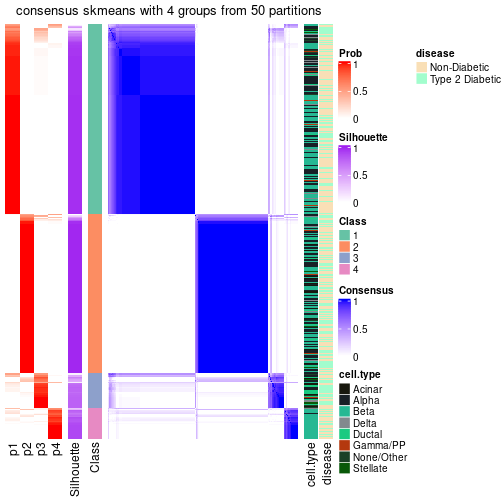
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
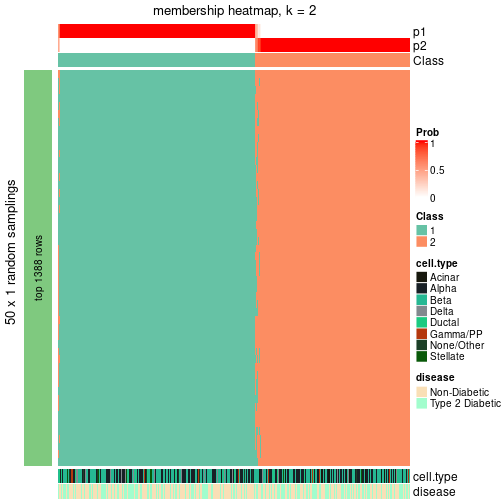
membership_heatmap(res, k = 3)
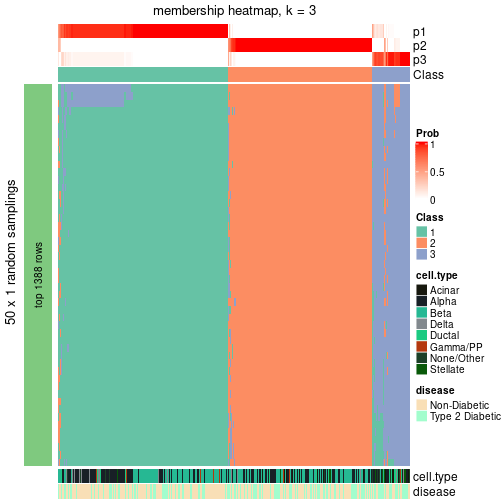
membership_heatmap(res, k = 4)
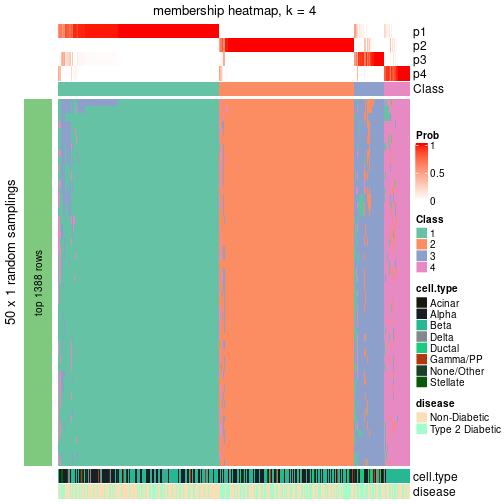
As soon as the classes for columns are determined, the signatures that are significantly different between subgroups can be looked for. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
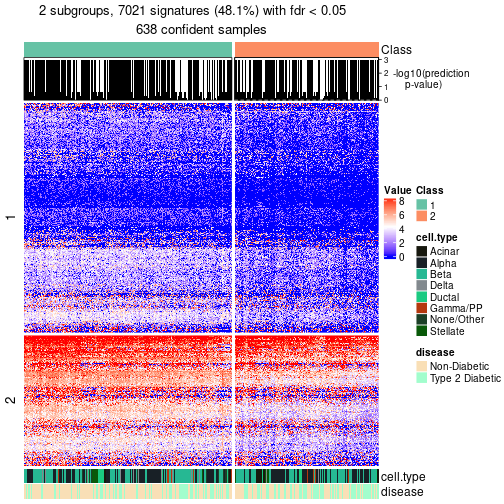
get_signatures(res, k = 3, scale_rows = FALSE)
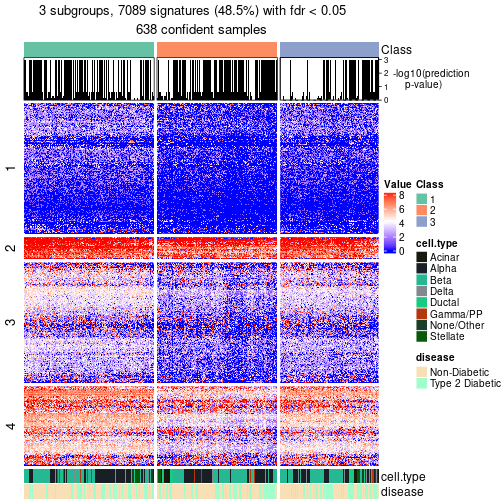
get_signatures(res, k = 4, scale_rows = FALSE)
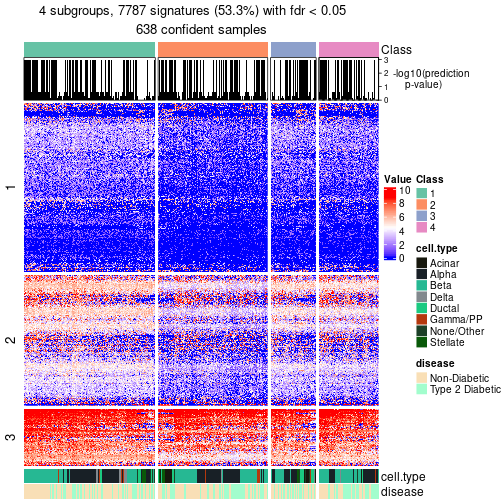
Compare the overlap of signatures from different k:
compare_signatures(res)
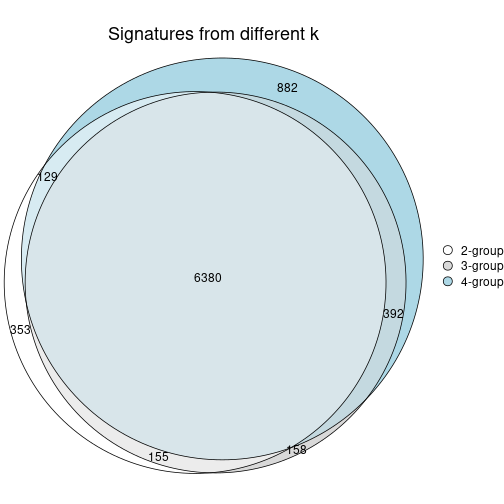
get_signature() returns a data frame invisibly. To get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows (which is done by automatically selecting number of clusters).If there are too many signatures, top_signatures = ... can be set to only show the
signatures with the highest FDRs:
# code only for demonstration
# e.g. to show the top 500 most significant rows
tb = get_signature(res, k = ..., top_signatures = 500)
If the signatures are defined as these which are uniquely high in current group, diff_method argument
can be set to "uniquely_high_in_one_group":
# code only for demonstration
tb = get_signature(res, k = ..., diff_method = "uniquely_high_in_one_group")
UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
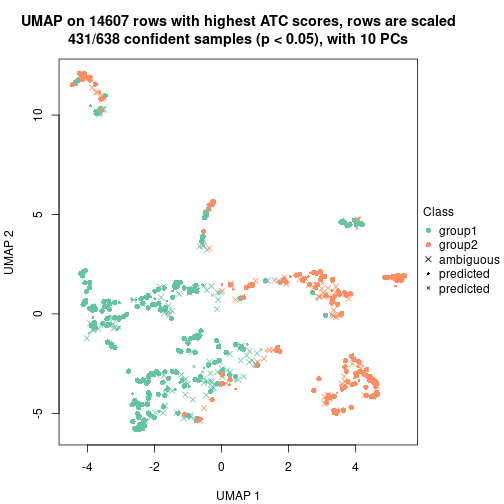
dimension_reduction(res, k = 3, method = "UMAP")

dimension_reduction(res, k = 4, method = "UMAP")
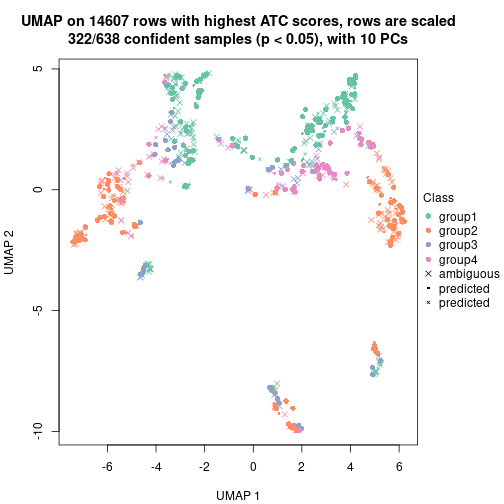
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)

Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n_sample cell.type(p-value) disease(p-value) k
#> ATC:skmeans 431 6.08e-03 0.01308 2
#> ATC:skmeans 298 1.72e-15 0.00263 3
#> ATC:skmeans 322 4.28e-17 0.15239 4
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
Parent node: Node0. Child nodes: Node011 , Node012 , Node021 , Node022 , Node023 , Node024-leaf .
The object with results only for a single top-value method and a single partitioning method can be extracted as:
res = res_rh["01"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4.
#> On a matrix with 13874 rows and 377 columns.
#> Top rows (1387) are extracted by 'ATC' method.
#> Subgroups are detected by 'skmeans' method.
#> Performed in total 150 partitions by row resampling.
#> Best k for subgroups seems to be 4.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_partitions"
#> [7] "compare_signatures" "consensus_heatmap" "dimension_reduction"
#> [10] "functional_enrichment" "get_anno_col" "get_anno"
#> [13] "get_classes" "get_consensus" "get_matrix"
#> [16] "get_membership" "get_param" "get_signatures"
#> [19] "get_stats" "is_best_k" "is_stable_k"
#> [22] "membership_heatmap" "ncol" "nrow"
#> [25] "plot_ecdf" "predict_classes" "rownames"
#> [28] "select_partition_number" "show" "suggest_best_k"
#> [31] "test_to_known_factors" "top_rows_heatmap"
collect_plots() function collects all the plots made from res for all k (number of subgroups)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
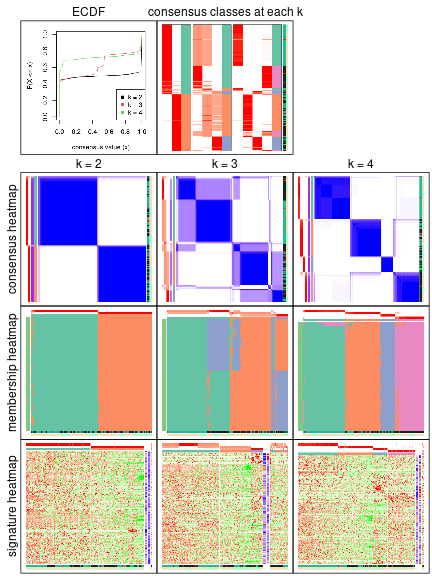
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, higher 1-PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
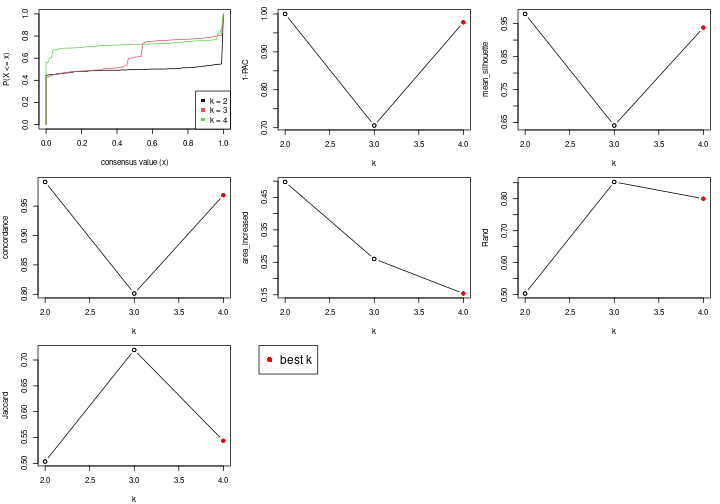
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 1.000 0.979 0.991 0.498 0.503 0.503
#> 3 3 0.706 0.641 0.801 0.260 0.852 0.719
#> 4 4 0.978 0.938 0.969 0.154 0.800 0.544
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 4
#> attr(,"optional")
#> [1] 2
There is also optional best \(k\) = 2 that is worth to check.
Following is the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall subgroup
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> 10th_C10_S104 2 0.000 0.994 0.00 1.00
#> 10th_C13_S61 1 0.000 0.989 1.00 0.00
#> 10th_C14_S53 2 0.000 0.994 0.00 1.00
#> 10th_C16_S105 2 0.000 0.994 0.00 1.00
#> 10th_C19_S62 1 0.000 0.989 1.00 0.00
#> 10th_C1_S59 2 0.000 0.994 0.00 1.00
#> 10th_C20_S54 2 0.000 0.994 0.00 1.00
#> 10th_C23_S98 2 0.000 0.994 0.00 1.00
#> 10th_C24_S90 2 0.000 0.994 0.00 1.00
#> 10th_C30_S107 2 0.000 0.994 0.00 1.00
#> 10th_C31_S48 2 0.000 0.994 0.00 1.00
#> 10th_C41_S101 2 0.000 0.994 0.00 1.00
#> 10th_C45_S66 2 0.000 0.994 0.00 1.00
#> 10th_C46_S94 2 0.000 0.994 0.00 1.00
#> 10th_C4_S103 2 0.000 0.994 0.00 1.00
#> 10th_C54_S124 2 0.000 0.994 0.00 1.00
#> 10th_C56_S74 2 0.000 0.994 0.00 1.00
#> 10th_C68_S75 2 0.000 0.994 0.00 1.00
#> 10th_C73_S84 2 0.000 0.994 0.00 1.00
#> 10th_C74_S76 2 0.000 0.994 0.00 1.00
#> 10th_C76_S128 2 0.000 0.994 0.00 1.00
#> 10th_C7_S60 2 0.000 0.994 0.00 1.00
#> 10th_C81_S70 1 0.000 0.989 1.00 0.00
#> 10th_C84_S115 1 0.000 0.989 1.00 0.00
#> 10th_C85_S86 2 0.000 0.994 0.00 1.00
#> 10th_C88_S130 2 0.000 0.994 0.00 1.00
#> 10th_C8_S52 2 0.000 0.994 0.00 1.00
#> 10th_C90_S116 2 0.000 0.994 0.00 1.00
#> 10th_C96_S117 2 0.000 0.994 0.00 1.00
#> 11th-C16_S64 2 0.000 0.994 0.00 1.00
#> 11th-C24_S49 2 0.000 0.994 0.00 1.00
#> 11th-C33_S20 2 0.000 0.994 0.00 1.00
#> 11th-C36_S67 2 0.000 0.994 0.00 1.00
#> 11th-C39_S21 2 0.000 0.994 0.00 1.00
#> 11th-C40_S52 2 0.000 0.994 0.00 1.00
#> 11th-C41_S60 1 0.000 0.989 1.00 0.00
#> 11th-C44_S15 1 0.000 0.989 1.00 0.00
#> 11th-C49_S23 1 0.000 0.989 1.00 0.00
#> 11th-C51_S39 1 0.000 0.989 1.00 0.00
#> 11th-C53_S78 1 0.327 0.931 0.94 0.06
#> 11th-C58_S71 2 0.000 0.994 0.00 1.00
#> 11th-C5_S54 2 0.000 0.994 0.00 1.00
#> 11th-C61_S25 2 0.000 0.994 0.00 1.00
#> 11th-C66_S88 1 0.000 0.989 1.00 0.00
#> 11th-C68_S34 2 0.000 0.994 0.00 1.00
#> 11th-C7_S16 1 0.000 0.989 1.00 0.00
#> 12th-C11_S147 2 0.000 0.994 0.00 1.00
#> 12th-C12_S139 2 0.000 0.994 0.00 1.00
#> 12th-C14_S190 1 0.000 0.989 1.00 0.00
#> 12th-C20_S191 2 0.000 0.994 0.00 1.00
#> 12th-C24_S141 1 0.000 0.989 1.00 0.00
#> 12th-C25_S185 2 0.000 0.994 0.00 1.00
#> 12th-C26_S192 2 0.000 0.994 0.00 1.00
#> 12th-C28_S142 2 0.000 0.994 0.00 1.00
#> 12th-C29_S150 1 0.000 0.989 1.00 0.00
#> 12th-C30_S157 2 0.000 0.994 0.00 1.00
#> 12th-C33_S200 2 0.000 0.994 0.00 1.00
#> 12th-C42_S159 1 0.000 0.989 1.00 0.00
#> 12th-C46_S145 2 0.000 0.994 0.00 1.00
#> 12th-C48_S160 2 0.000 0.994 0.00 1.00
#> 12th-C51_S217 2 0.000 0.994 0.00 1.00
#> 12th-C55_S203 1 0.000 0.989 1.00 0.00
#> 12th-C58_S162 1 0.000 0.989 1.00 0.00
#> 12th-C59_S169 1 0.000 0.989 1.00 0.00
#> 12th-C60_S176 1 0.000 0.989 1.00 0.00
#> 12th-C63_S219 2 0.000 0.994 0.00 1.00
#> 12th-C64_S163 1 0.000 0.989 1.00 0.00
#> 12th-C65_S170 1 0.000 0.989 1.00 0.00
#> 12th-C69_S135 2 0.000 0.994 0.00 1.00
#> 12th-C74_S214 1 0.000 0.989 1.00 0.00
#> 12th-C76_S177 1 0.000 0.989 1.00 0.00
#> 12th-C7_S196 1 0.000 0.989 1.00 0.00
#> 12th-C80_S215 2 0.000 0.994 0.00 1.00
#> 12th-C81_S207 2 0.000 0.994 0.00 1.00
#> 12th-C84_S165 1 0.000 0.989 1.00 0.00
#> 12th-C85_S137 2 0.000 0.994 0.00 1.00
#> 12th-C90_S166 1 0.000 0.989 1.00 0.00
#> 12th-C94_S180 2 0.000 0.994 0.00 1.00
#> 12th-C95_S174 1 0.000 0.989 1.00 0.00
#> 12th-C96_S167 1 0.000 0.989 1.00 0.00
#> 13th_C12_S178 2 0.000 0.994 0.00 1.00
#> 13th_C13_S149 2 0.000 0.994 0.00 1.00
#> 13th_C16_S193 2 0.000 0.994 0.00 1.00
#> 13th_C23_S187 2 0.000 0.994 0.00 1.00
#> 13th_C34_S181 1 0.000 0.989 1.00 0.00
#> 13th_C39_S153 2 0.000 0.994 0.00 1.00
#> 13th_C60_S213 2 0.000 0.994 0.00 1.00
#> 13th_C66_S214 1 0.000 0.989 1.00 0.00
#> 13th_C76_S216 1 0.000 0.989 1.00 0.00
#> 13th_C94_S219 2 0.000 0.994 0.00 1.00
#> 13th_C96_S204 2 0.000 0.994 0.00 1.00
#> 1st-61_S27 1 0.000 0.989 1.00 0.00
#> 1st-C11_S58 1 0.000 0.989 1.00 0.00
#> 1st-C19_S20 1 0.000 0.989 1.00 0.00
#> 1st-C21_S4 2 0.000 0.994 0.00 1.00
#> 1st-C32_S14 1 0.000 0.989 1.00 0.00
#> 1st-C34_S54 2 0.000 0.994 0.00 1.00
#> 1st-C42_S71 1 0.000 0.989 1.00 0.00
#> 1st-C50_S33 1 0.000 0.989 1.00 0.00
#> 1st-C56_S34 1 0.000 0.989 1.00 0.00
#> 1st-C57_S42 1 0.000 0.989 1.00 0.00
#> 1st-C58_S76 1 0.000 0.989 1.00 0.00
#> 1st-C64_S79 1 0.000 0.989 1.00 0.00
#> 1st-C68_S36 1 0.000 0.989 1.00 0.00
#> 1st-C69_S44 2 0.000 0.994 0.00 1.00
#> 1st-C71_S83 2 0.000 0.994 0.00 1.00
#> 1st-C73_S45 1 0.000 0.989 1.00 0.00
#> 1st-C75_S29 1 0.000 0.989 1.00 0.00
#> 1st-C77_S86 1 0.000 0.989 1.00 0.00
#> 1st-C78_S85 1 0.000 0.989 1.00 0.00
#> 1st-C80_S38 1 0.000 0.989 1.00 0.00
#> 1st-C90_S91 1 0.000 0.989 1.00 0.00
#> 2nd-C11_S20 1 0.000 0.989 1.00 0.00
#> 2nd-C15_S25 1 0.000 0.989 1.00 0.00
#> 2nd-C16_S33 1 0.000 0.989 1.00 0.00
#> 2nd-C17_S32 1 0.000 0.989 1.00 0.00
#> 2nd-C21_S37 1 0.000 0.989 1.00 0.00
#> 2nd-C25_S49 2 0.000 0.994 0.00 1.00
#> 2nd-C26_S50 1 0.000 0.989 1.00 0.00
#> 2nd-C29_S56 2 0.000 0.994 0.00 1.00
#> 2nd-C31_S61 2 0.000 0.994 0.00 1.00
#> 2nd-C32_S62 1 0.000 0.989 1.00 0.00
#> 2nd-C38_S74 1 0.000 0.989 1.00 0.00
#> 2nd-C39_S75 1 0.000 0.989 1.00 0.00
#> 2nd-C47_S92 2 0.000 0.994 0.00 1.00
#> 2nd-C54_S12 2 0.000 0.994 0.00 1.00
#> 2nd-C57_S18 2 0.000 0.994 0.00 1.00
#> 2nd-C62_S29 1 0.000 0.989 1.00 0.00
#> 2nd-C67_S40 1 0.000 0.989 1.00 0.00
#> 2nd-C6_S7 2 0.000 0.994 0.00 1.00
#> 2nd-C72_S48 1 0.722 0.755 0.80 0.20
#> 2nd-C74_S53 2 0.000 0.994 0.00 1.00
#> 2nd-C75_S52 1 0.000 0.989 1.00 0.00
#> 2nd-C76_S60 2 0.000 0.994 0.00 1.00
#> 2nd-C77_S59 1 0.000 0.989 1.00 0.00
#> 2nd-C80_S65 1 0.000 0.989 1.00 0.00
#> 2nd-C81_S64 2 0.000 0.994 0.00 1.00
#> 2nd-C83_S71 2 0.141 0.974 0.02 0.98
#> 2nd-C86_S77 1 0.000 0.989 1.00 0.00
#> 2nd-C88_S84 1 0.000 0.989 1.00 0.00
#> 2nd-C8_S14 1 0.000 0.989 1.00 0.00
#> 2nd-C93_S88 1 0.000 0.989 1.00 0.00
#> 2nd-C95_S95 1 0.000 0.989 1.00 0.00
#> 3rd-C11_S58 1 0.000 0.989 1.00 0.00
#> 3rd-C12_S68 1 0.000 0.989 1.00 0.00
#> 3rd-C18_S80 2 0.000 0.994 0.00 1.00
#> 3rd-C1_S39 2 0.000 0.994 0.00 1.00
#> 3rd-C20_S22 2 0.000 0.994 0.00 1.00
#> 3rd-C21_S11 2 0.000 0.994 0.00 1.00
#> 3rd-C26_S28 2 0.000 0.994 0.00 1.00
#> 3rd-C27_S49 1 0.995 0.158 0.54 0.46
#> 3rd-C33_S50 1 0.000 0.989 1.00 0.00
#> 3rd-C35_S23 1 0.000 0.989 1.00 0.00
#> 3rd-C36_S2 1 0.000 0.989 1.00 0.00
#> 3rd-C40_S57 2 0.000 0.994 0.00 1.00
#> 3rd-C42_S74 2 0.000 0.994 0.00 1.00
#> 3rd-C46_S93 2 0.000 0.994 0.00 1.00
#> 3rd-C47_S35 1 0.000 0.989 1.00 0.00
#> 3rd-C49_S60 1 0.000 0.989 1.00 0.00
#> 3rd-C4_S25 1 0.000 0.989 1.00 0.00
#> 3rd-C53_S67 1 0.000 0.989 1.00 0.00
#> 3rd-C57_S5 1 0.000 0.989 1.00 0.00
#> 3rd-C58_S3 1 0.000 0.989 1.00 0.00
#> 3rd-C59_S91 1 0.000 0.989 1.00 0.00
#> 3rd-C65_S20 1 0.000 0.989 1.00 0.00
#> 3rd-C67_S69 2 0.584 0.836 0.14 0.86
#> 3rd-C68_S13 2 0.000 0.994 0.00 1.00
#> 3rd-C6_S44 1 0.000 0.989 1.00 0.00
#> 3rd-C71_S80 1 0.000 0.989 1.00 0.00
#> 3rd-C76_S22 2 0.000 0.994 0.00 1.00
#> 3rd-C79_S67 1 0.000 0.989 1.00 0.00
#> 3rd-C82_S11 1 0.000 0.989 1.00 0.00
#> 3rd-C84_S75 1 0.000 0.989 1.00 0.00
#> 3rd-C85_S79 1 0.000 0.989 1.00 0.00
#> 3rd-C86_S85 2 0.000 0.994 0.00 1.00
#> 3rd-C87_S88 2 0.000 0.994 0.00 1.00
#> 3rd-C88_S24 1 0.000 0.989 1.00 0.00
#> 3rd-C91_S91 1 0.000 0.989 1.00 0.00
#> 3rd-C92_S86 1 0.000 0.989 1.00 0.00
#> 3rd-C95_S81 1 0.000 0.989 1.00 0.00
#> 3rd-C9_S5 1 0.000 0.989 1.00 0.00
#> 4th-61_S28 1 0.000 0.989 1.00 0.00
#> 4th-C12_S19 2 0.000 0.994 0.00 1.00
#> 4th-C14_S26 1 0.000 0.989 1.00 0.00
#> 4th-C18_S31 1 0.141 0.970 0.98 0.02
#> 4th-C23_S44 2 0.000 0.994 0.00 1.00
#> 4th-C24_S43 1 0.000 0.989 1.00 0.00
#> 4th-C26_S50 1 0.000 0.989 1.00 0.00
#> 4th-C28_S55 2 0.000 0.994 0.00 1.00
#> 4th-C29_S56 2 0.000 0.994 0.00 1.00
#> 4th-C32_S62 2 0.000 0.994 0.00 1.00
#> 4th-C33_S63 2 0.000 0.994 0.00 1.00
#> 4th-C36_S69 1 0.000 0.989 1.00 0.00
#> 4th-C40_S79 1 0.000 0.989 1.00 0.00
#> 4th-C43_S85 2 0.000 0.994 0.00 1.00
#> 4th-C49_S4 2 0.000 0.994 0.00 1.00
#> 4th-C4_S9 1 0.000 0.989 1.00 0.00
#> 4th-C51_S6 2 0.000 0.994 0.00 1.00
#> 4th-C56_S17 1 0.000 0.989 1.00 0.00
#> 4th-C59_S23 2 0.000 0.994 0.00 1.00
#> 4th-C5_S8 1 0.000 0.989 1.00 0.00
#> 4th-C62_S29 1 0.000 0.989 1.00 0.00
#> 4th-C63_S30 2 0.000 0.994 0.00 1.00
#> 4th-C64_S34 1 0.000 0.989 1.00 0.00
#> 4th-C66_S36 1 0.000 0.989 1.00 0.00
#> 4th-C67_S40 1 0.000 0.989 1.00 0.00
#> 4th-C69_S42 2 0.000 0.994 0.00 1.00
#> 4th-C70_S46 2 0.000 0.994 0.00 1.00
#> 4th-C73_S54 1 0.000 0.989 1.00 0.00
#> 4th-C75_S52 1 0.000 0.989 1.00 0.00
#> 4th-C78_S58 2 0.000 0.994 0.00 1.00
#> 4th-C79_S66 1 0.000 0.989 1.00 0.00
#> 4th-C7_S15 1 0.000 0.989 1.00 0.00
#> 4th-C80_S65 1 0.000 0.989 1.00 0.00
#> 4th-C81_S64 2 0.000 0.994 0.00 1.00
#> 4th-C82_S72 1 0.000 0.989 1.00 0.00
#> 4th-C83_S71 1 0.000 0.989 1.00 0.00
#> 4th-C85_S78 1 0.000 0.989 1.00 0.00
#> 4th-C86_S77 1 0.000 0.989 1.00 0.00
#> 4th-C87_S76 2 0.000 0.994 0.00 1.00
#> 4th-C88_S84 1 0.000 0.989 1.00 0.00
#> 4th-C89_S83 1 0.000 0.989 1.00 0.00
#> 4th-C8_S14 2 0.000 0.994 0.00 1.00
#> 4th-C92_S89 1 0.634 0.812 0.84 0.16
#> 4th-C94_S96 1 0.000 0.989 1.00 0.00
#> 4th-C95_S95 2 0.000 0.994 0.00 1.00
#> 4th-C96_S94 1 0.000 0.989 1.00 0.00
#> 5th-C12_S90 2 0.000 0.994 0.00 1.00
#> 5th-C19_S104 2 0.000 0.994 0.00 1.00
#> 5th-C21_S102 2 0.981 0.268 0.42 0.58
#> 5th-C30_S105 2 0.000 0.994 0.00 1.00
#> 5th-C34_S108 1 0.904 0.536 0.68 0.32
#> 5th-C35_S109 1 0.000 0.989 1.00 0.00
#> 5th-C47_S118 2 0.000 0.994 0.00 1.00
#> 5th-C49_S89 1 0.000 0.989 1.00 0.00
#> 5th-C50_S90 2 0.000 0.994 0.00 1.00
#> 5th-C54_S89 2 0.000 0.994 0.00 1.00
#> 5th-C57_S96 2 0.000 0.994 0.00 1.00
#> 5th-C59_S94 2 0.000 0.994 0.00 1.00
#> 5th-C5_S85 1 0.000 0.989 1.00 0.00
#> 5th-C64_S99 2 0.000 0.994 0.00 1.00
#> 5th-C66_S101 2 0.000 0.994 0.00 1.00
#> 5th-C68_S106 2 0.000 0.994 0.00 1.00
#> 5th-C69_S107 2 0.000 0.994 0.00 1.00
#> 5th-C74_S110 2 0.000 0.994 0.00 1.00
#> 5th-C77_S107 2 0.000 0.994 0.00 1.00
#> 5th-C7_S93 1 0.000 0.989 1.00 0.00
#> 5th-C90_S115 1 0.000 0.989 1.00 0.00
#> 5th-C92_S124 2 0.000 0.994 0.00 1.00
#> 5th-C9_S92 1 0.000 0.989 1.00 0.00
#> 6th-C12_S18 1 0.000 0.989 1.00 0.00
#> 6th-C16_S29 2 0.000 0.994 0.00 1.00
#> 6th-C20_S34 1 0.000 0.989 1.00 0.00
#> 6th-C21_S33 1 0.795 0.691 0.76 0.24
#> 6th-C22_S39 1 0.000 0.989 1.00 0.00
#> 6th-C23_S38 1 0.000 0.989 1.00 0.00
#> 6th-C24_S37 1 0.000 0.989 1.00 0.00
#> 6th-C29_S50 1 0.000 0.989 1.00 0.00
#> 6th-C2_S2 1 0.000 0.989 1.00 0.00
#> 6th-C30_S51 1 0.000 0.989 1.00 0.00
#> 6th-C40_S73 1 0.000 0.989 1.00 0.00
#> 6th-C42_S75 1 0.795 0.691 0.76 0.24
#> 6th-C51_S6 1 0.000 0.989 1.00 0.00
#> 6th-C53_S10 2 0.000 0.994 0.00 1.00
#> 6th-C54_S11 1 0.000 0.989 1.00 0.00
#> 6th-C59_S21 1 0.000 0.989 1.00 0.00
#> 6th-C5_S8 2 0.000 0.994 0.00 1.00
#> 6th-C63_S26 1 0.000 0.989 1.00 0.00
#> 6th-C65_S31 2 0.000 0.994 0.00 1.00
#> 6th-C66_S32 1 0.000 0.989 1.00 0.00
#> 6th-C71_S41 1 0.000 0.989 1.00 0.00
#> 6th-C73_S48 1 0.000 0.989 1.00 0.00
#> 6th-C75_S46 1 0.000 0.989 1.00 0.00
#> 6th-C77_S53 1 0.000 0.989 1.00 0.00
#> 6th-C79_S60 1 0.000 0.989 1.00 0.00
#> 6th-C80_S59 1 0.000 0.989 1.00 0.00
#> 6th-C85_S72 1 0.000 0.989 1.00 0.00
#> 6th-C87_S70 1 0.242 0.951 0.96 0.04
#> 6th-C91_S84 2 0.000 0.994 0.00 1.00
#> 6th-C93_S82 2 0.529 0.862 0.12 0.88
#> 7th-C10_S19 1 0.000 0.989 1.00 0.00
#> 7th-C11_S18 1 0.000 0.989 1.00 0.00
#> 7th-C14_S24 1 0.000 0.989 1.00 0.00
#> 7th-C15_S23 2 0.000 0.994 0.00 1.00
#> 7th-C17_S29 2 0.000 0.994 0.00 1.00
#> 7th-C24_S40 1 0.469 0.887 0.90 0.10
#> 7th-C25_S43 1 0.000 0.989 1.00 0.00
#> 7th-C31_S53 1 0.000 0.989 1.00 0.00
#> 7th-C32_S54 2 0.000 0.994 0.00 1.00
#> 7th-C34_S59 2 0.584 0.836 0.14 0.86
#> 7th-C36_S61 1 0.000 0.989 1.00 0.00
#> 7th-C40_S70 2 0.000 0.994 0.00 1.00
#> 7th-C44_S76 2 0.000 0.994 0.00 1.00
#> 7th-C45_S77 1 0.000 0.989 1.00 0.00
#> 7th-C50_S5 1 0.000 0.989 1.00 0.00
#> 7th-C53_S10 1 0.000 0.989 1.00 0.00
#> 7th-C56_S15 2 0.000 0.994 0.00 1.00
#> 7th-C58_S20 1 0.000 0.989 1.00 0.00
#> 7th-C59_S21 1 0.000 0.989 1.00 0.00
#> 7th-C62_S27 1 0.000 0.989 1.00 0.00
#> 7th-C64_S31 1 0.000 0.989 1.00 0.00
#> 7th-C66_S33 1 0.000 0.989 1.00 0.00
#> 7th-C68_S38 2 0.000 0.994 0.00 1.00
#> 7th-C69_S39 2 0.000 0.994 0.00 1.00
#> 7th-C72_S42 2 0.634 0.808 0.16 0.84
#> 7th-C73_S47 1 0.000 0.989 1.00 0.00
#> 7th-C77_S51 1 0.000 0.989 1.00 0.00
#> 7th-C79_S58 1 0.000 0.989 1.00 0.00
#> 7th-C80_S57 1 0.000 0.989 1.00 0.00
#> 7th-C82_S64 1 0.000 0.989 1.00 0.00
#> 7th-C84_S62 1 0.000 0.989 1.00 0.00
#> 7th-C88_S75 2 0.000 0.994 0.00 1.00
#> 7th-C89_S74 1 0.000 0.989 1.00 0.00
#> 7th-C8_S13 1 0.000 0.989 1.00 0.00
#> 7th-C90_S73 1 0.000 0.989 1.00 0.00
#> 7th-C96_S82 1 0.000 0.989 1.00 0.00
#> 8th-C10_S100 1 0.000 0.989 1.00 0.00
#> 8th-C11_S99 2 0.000 0.994 0.00 1.00
#> 8th-C20_S116 2 0.000 0.994 0.00 1.00
#> 8th-C24_S120 1 0.000 0.989 1.00 0.00
#> 8th-C2_S85 1 0.000 0.989 1.00 0.00
#> 8th-C34_S141 2 0.000 0.994 0.00 1.00
#> 8th-C44_S155 1 0.000 0.989 1.00 0.00
#> 8th-C55_S96 1 0.827 0.657 0.74 0.26
#> 8th-C57_S98 1 0.000 0.989 1.00 0.00
#> 8th-C58_S101 1 0.402 0.909 0.92 0.08
#> 8th-C59_S102 2 0.000 0.994 0.00 1.00
#> 8th-C61_S107 2 0.000 0.994 0.00 1.00
#> 8th-C64_S112 2 0.000 0.994 0.00 1.00
#> 8th-C65_S113 1 0.000 0.989 1.00 0.00
#> 8th-C67_S117 1 0.000 0.989 1.00 0.00
#> 8th-C6_S88 2 0.000 0.994 0.00 1.00
#> 8th-C73_S130 2 0.000 0.994 0.00 1.00
#> 8th-C74_S129 1 0.000 0.989 1.00 0.00
#> 8th-C7_S95 2 0.000 0.994 0.00 1.00
#> 8th-C85_S150 1 0.000 0.989 1.00 0.00
#> 8th-C87_S148 1 0.000 0.989 1.00 0.00
#> 8th-C92_S157 2 0.000 0.994 0.00 1.00
#> 8th-C95_S161 2 0.000 0.994 0.00 1.00
#> 9th-C10_S18 1 0.000 0.989 1.00 0.00
#> 9th-C11_S17 1 0.000 0.989 1.00 0.00
#> 9th-C15_S22 2 0.000 0.994 0.00 1.00
#> 9th-C16_S30 2 0.000 0.994 0.00 1.00
#> 9th-C17_S29 2 0.000 0.994 0.00 1.00
#> 9th-C19_S36 2 0.000 0.994 0.00 1.00
#> 9th-C1_S3 1 0.000 0.989 1.00 0.00
#> 9th-C28_S50 2 0.000 0.994 0.00 1.00
#> 9th-C29_S51 2 0.000 0.994 0.00 1.00
#> 9th-C30_S52 2 0.000 0.994 0.00 1.00
#> 9th-C36_S59 2 0.000 0.994 0.00 1.00
#> 9th-C38_S64 1 0.000 0.989 1.00 0.00
#> 9th-C3_S1 1 0.000 0.989 1.00 0.00
#> 9th-C40_S69 2 0.000 0.994 0.00 1.00
#> 9th-C41_S70 1 0.000 0.989 1.00 0.00
#> 9th-C46_S79 1 0.000 0.989 1.00 0.00
#> 9th-C57_S16 1 0.327 0.931 0.94 0.06
#> 9th-C5_S8 2 0.000 0.994 0.00 1.00
#> 9th-C61_S25 2 0.000 0.994 0.00 1.00
#> 9th-C62_S26 2 0.000 0.994 0.00 1.00
#> 9th-C64_S31 2 0.000 0.994 0.00 1.00
#> 9th-C65_S32 2 0.000 0.994 0.00 1.00
#> 9th-C66_S33 2 0.000 0.994 0.00 1.00
#> 9th-C67_S37 2 0.000 0.994 0.00 1.00
#> 9th-C6_S7 1 0.000 0.989 1.00 0.00
#> 9th-C70_S42 1 0.000 0.989 1.00 0.00
#> 9th-C74_S48 2 0.000 0.994 0.00 1.00
#> 9th-C77_S53 2 0.000 0.994 0.00 1.00
#> 9th-C80_S56 1 0.000 0.989 1.00 0.00
#> 9th-C81_S55 1 0.000 0.989 1.00 0.00
#> 9th-C83_S61 1 0.000 0.989 1.00 0.00
#> 9th-C84_S60 2 0.000 0.994 0.00 1.00
#> 9th-C86_S67 1 0.000 0.989 1.00 0.00
#> 9th-C89_S72 1 0.000 0.989 1.00 0.00
#> 9th-C8_S14 1 0.000 0.989 1.00 0.00
#> 9th-C93_S76 1 0.000 0.989 1.00 0.00
#> 9th-C96_S81 2 0.000 0.994 0.00 1.00
#> 9th-C9_S13 1 0.469 0.887 0.90 0.10
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> 10th_C10_S104 2 0.6280 0.7530 0.00 0.54 0.46
#> 10th_C13_S61 1 0.6280 0.7963 0.54 0.46 0.00
#> 10th_C14_S53 2 0.6280 0.7530 0.00 0.54 0.46
#> 10th_C16_S105 2 0.6280 0.7530 0.00 0.54 0.46
#> 10th_C19_S62 3 0.8853 0.3061 0.14 0.32 0.54
#> 10th_C1_S59 2 0.6280 0.7530 0.00 0.54 0.46
#> 10th_C20_S54 2 0.6280 0.7530 0.00 0.54 0.46
#> 10th_C23_S98 2 0.6280 0.7530 0.00 0.54 0.46
#> 10th_C24_S90 2 0.6280 0.7530 0.00 0.54 0.46
#> 10th_C30_S107 2 0.6280 0.7530 0.00 0.54 0.46
#> 10th_C31_S48 2 0.6280 0.7530 0.00 0.54 0.46
#> 10th_C41_S101 2 0.6280 0.7530 0.00 0.54 0.46
#> 10th_C45_S66 2 0.6280 0.7530 0.00 0.54 0.46
#> 10th_C46_S94 3 0.0000 0.7287 0.00 0.00 1.00
#> 10th_C4_S103 3 0.0000 0.7287 0.00 0.00 1.00
#> 10th_C54_S124 2 0.6280 0.7530 0.00 0.54 0.46
#> 10th_C56_S74 3 0.0000 0.7287 0.00 0.00 1.00
#> 10th_C68_S75 2 0.6280 0.7530 0.00 0.54 0.46
#> 10th_C73_S84 3 0.0000 0.7287 0.00 0.00 1.00
#> 10th_C74_S76 2 0.6280 0.7530 0.00 0.54 0.46
#> 10th_C76_S128 2 0.6280 0.7530 0.00 0.54 0.46
#> 10th_C7_S60 3 0.0000 0.7287 0.00 0.00 1.00
#> 10th_C81_S70 1 0.6280 0.7963 0.54 0.46 0.00
#> 10th_C84_S115 1 0.6280 0.7963 0.54 0.46 0.00
#> 10th_C85_S86 2 0.6280 0.7530 0.00 0.54 0.46
#> 10th_C88_S130 3 0.0000 0.7287 0.00 0.00 1.00
#> 10th_C8_S52 2 0.6280 0.7530 0.00 0.54 0.46
#> 10th_C90_S116 2 0.6280 0.7530 0.00 0.54 0.46
#> 10th_C96_S117 2 0.6280 0.3078 0.46 0.54 0.00
#> 11th-C16_S64 2 0.6280 0.7530 0.00 0.54 0.46
#> 11th-C24_S49 3 0.0000 0.7287 0.00 0.00 1.00
#> 11th-C33_S20 2 0.6280 0.7530 0.00 0.54 0.46
#> 11th-C36_S67 2 0.6280 0.7530 0.00 0.54 0.46
#> 11th-C39_S21 2 0.6280 0.7530 0.00 0.54 0.46
#> 11th-C40_S52 3 0.0000 0.7287 0.00 0.00 1.00
#> 11th-C41_S60 1 0.6280 0.7963 0.54 0.46 0.00
#> 11th-C44_S15 1 0.6280 0.7963 0.54 0.46 0.00
#> 11th-C49_S23 1 0.6280 0.7963 0.54 0.46 0.00
#> 11th-C51_S39 1 0.6280 0.7963 0.54 0.46 0.00
#> 11th-C53_S78 2 0.7578 -0.7611 0.46 0.50 0.04
#> 11th-C58_S71 3 0.0000 0.7287 0.00 0.00 1.00
#> 11th-C5_S54 2 0.7029 0.7328 0.02 0.54 0.44
#> 11th-C61_S25 2 0.6280 0.7530 0.00 0.54 0.46
#> 11th-C66_S88 1 0.6280 0.7963 0.54 0.46 0.00
#> 11th-C68_S34 3 0.6302 -0.6594 0.00 0.48 0.52
#> 11th-C7_S16 3 0.8853 0.3061 0.14 0.32 0.54
#> 12th-C11_S147 2 0.6280 0.7530 0.00 0.54 0.46
#> 12th-C12_S139 2 0.6280 0.7530 0.00 0.54 0.46
#> 12th-C14_S190 2 0.6309 -0.7871 0.50 0.50 0.00
#> 12th-C20_S191 2 0.6280 0.7530 0.00 0.54 0.46
#> 12th-C24_S141 1 0.6280 0.7963 0.54 0.46 0.00
#> 12th-C25_S185 2 0.6280 0.7530 0.00 0.54 0.46
#> 12th-C26_S192 2 0.6280 0.7530 0.00 0.54 0.46
#> 12th-C28_S142 2 0.6280 0.3078 0.46 0.54 0.00
#> 12th-C29_S150 1 0.0000 0.6005 1.00 0.00 0.00
#> 12th-C30_S157 2 0.6244 0.7275 0.00 0.56 0.44
#> 12th-C33_S200 2 0.5216 0.4663 0.00 0.74 0.26
#> 12th-C42_S159 1 0.6280 0.7963 0.54 0.46 0.00
#> 12th-C46_S145 3 0.0000 0.7287 0.00 0.00 1.00
#> 12th-C48_S160 2 0.6280 0.7530 0.00 0.54 0.46
#> 12th-C51_S217 2 0.6280 0.7530 0.00 0.54 0.46
#> 12th-C55_S203 1 0.6280 0.7963 0.54 0.46 0.00
#> 12th-C58_S162 1 0.0000 0.6005 1.00 0.00 0.00
#> 12th-C59_S169 1 0.6280 0.7963 0.54 0.46 0.00
#> 12th-C60_S176 1 0.6280 0.7963 0.54 0.46 0.00
#> 12th-C63_S219 2 0.6280 0.7530 0.00 0.54 0.46
#> 12th-C64_S163 1 0.6280 0.7963 0.54 0.46 0.00
#> 12th-C65_S170 1 0.6280 0.7963 0.54 0.46 0.00
#> 12th-C69_S135 3 0.0000 0.7287 0.00 0.00 1.00
#> 12th-C74_S214 1 0.6280 0.7963 0.54 0.46 0.00
#> 12th-C76_S177 1 0.6280 0.7963 0.54 0.46 0.00
#> 12th-C7_S196 1 0.6280 0.7963 0.54 0.46 0.00
#> 12th-C80_S215 3 0.2537 0.5821 0.00 0.08 0.92
#> 12th-C81_S207 2 0.6280 0.7530 0.00 0.54 0.46
#> 12th-C84_S165 1 0.6280 0.7963 0.54 0.46 0.00
#> 12th-C85_S137 2 0.6280 0.7530 0.00 0.54 0.46
#> 12th-C90_S166 1 0.6280 0.7963 0.54 0.46 0.00
#> 12th-C94_S180 3 0.0000 0.7287 0.00 0.00 1.00
#> 12th-C95_S174 1 0.0000 0.6005 1.00 0.00 0.00
#> 12th-C96_S167 1 0.6280 0.7963 0.54 0.46 0.00
#> 13th_C12_S178 2 0.5016 0.4371 0.00 0.76 0.24
#> 13th_C13_S149 2 0.6280 0.7530 0.00 0.54 0.46
#> 13th_C16_S193 2 0.6280 0.7530 0.00 0.54 0.46
#> 13th_C23_S187 2 0.6280 0.7530 0.00 0.54 0.46
#> 13th_C34_S181 1 0.6280 0.7963 0.54 0.46 0.00
#> 13th_C39_S153 2 0.6280 0.7530 0.00 0.54 0.46
#> 13th_C60_S213 2 0.6280 0.7530 0.00 0.54 0.46
#> 13th_C66_S214 1 0.4002 0.6662 0.84 0.16 0.00
#> 13th_C76_S216 1 0.0000 0.6005 1.00 0.00 0.00
#> 13th_C94_S219 2 0.6280 0.7530 0.00 0.54 0.46
#> 13th_C96_S204 2 0.6280 0.7530 0.00 0.54 0.46
#> 1st-61_S27 1 0.6280 0.7963 0.54 0.46 0.00
#> 1st-C11_S58 1 0.6280 0.7963 0.54 0.46 0.00
#> 1st-C19_S20 1 0.0000 0.6005 1.00 0.00 0.00
#> 1st-C21_S4 2 0.6280 0.3078 0.46 0.54 0.00
#> 1st-C32_S14 1 0.6280 0.7963 0.54 0.46 0.00
#> 1st-C34_S54 3 0.0000 0.7287 0.00 0.00 1.00
#> 1st-C42_S71 3 0.7517 0.2211 0.04 0.42 0.54
#> 1st-C50_S33 1 0.0000 0.6005 1.00 0.00 0.00
#> 1st-C56_S34 1 0.0000 0.6005 1.00 0.00 0.00
#> 1st-C57_S42 1 0.0000 0.6005 1.00 0.00 0.00
#> 1st-C58_S76 1 0.6280 0.7963 0.54 0.46 0.00
#> 1st-C64_S79 1 0.6280 0.7963 0.54 0.46 0.00
#> 1st-C68_S36 1 0.0000 0.6005 1.00 0.00 0.00
#> 1st-C69_S44 2 0.6280 0.7530 0.00 0.54 0.46
#> 1st-C71_S83 2 0.6280 0.7530 0.00 0.54 0.46
#> 1st-C73_S45 1 0.1529 0.5535 0.96 0.04 0.00
#> 1st-C75_S29 1 0.6192 0.7801 0.58 0.42 0.00
#> 1st-C77_S86 1 0.6280 0.7963 0.54 0.46 0.00
#> 1st-C78_S85 1 0.0000 0.6005 1.00 0.00 0.00
#> 1st-C80_S38 1 0.0000 0.6005 1.00 0.00 0.00
#> 1st-C90_S91 1 0.6280 0.7963 0.54 0.46 0.00
#> 2nd-C11_S20 1 0.0000 0.6005 1.00 0.00 0.00
#> 2nd-C15_S25 1 0.6280 0.7963 0.54 0.46 0.00
#> 2nd-C16_S33 1 0.0000 0.6005 1.00 0.00 0.00
#> 2nd-C17_S32 1 0.6280 0.7963 0.54 0.46 0.00
#> 2nd-C21_S37 1 0.6280 0.7963 0.54 0.46 0.00
#> 2nd-C25_S49 2 0.6280 0.7530 0.00 0.54 0.46
#> 2nd-C26_S50 1 0.0000 0.6005 1.00 0.00 0.00
#> 2nd-C29_S56 2 0.6280 0.7530 0.00 0.54 0.46
#> 2nd-C31_S61 2 0.6280 0.3078 0.46 0.54 0.00
#> 2nd-C32_S62 1 0.6280 0.7963 0.54 0.46 0.00
#> 2nd-C38_S74 1 0.6280 0.7963 0.54 0.46 0.00
#> 2nd-C39_S75 1 0.0000 0.6005 1.00 0.00 0.00
#> 2nd-C47_S92 2 0.6280 0.3078 0.46 0.54 0.00
#> 2nd-C54_S12 3 0.0000 0.7287 0.00 0.00 1.00
#> 2nd-C57_S18 2 0.7029 0.7327 0.02 0.54 0.44
#> 2nd-C62_S29 1 0.6280 0.7963 0.54 0.46 0.00
#> 2nd-C67_S40 1 0.0000 0.6005 1.00 0.00 0.00
#> 2nd-C6_S7 2 0.7901 0.3517 0.40 0.54 0.06
#> 2nd-C72_S48 2 0.2959 -0.0465 0.10 0.90 0.00
#> 2nd-C74_S53 2 0.6280 0.3078 0.46 0.54 0.00
#> 2nd-C75_S52 1 0.0000 0.6005 1.00 0.00 0.00
#> 2nd-C76_S60 2 0.6280 0.7530 0.00 0.54 0.46
#> 2nd-C77_S59 1 0.0000 0.6005 1.00 0.00 0.00
#> 2nd-C80_S65 1 0.0000 0.6005 1.00 0.00 0.00
#> 2nd-C81_S64 2 0.6280 0.7530 0.00 0.54 0.46
#> 2nd-C83_S71 3 0.6280 0.3760 0.46 0.00 0.54
#> 2nd-C86_S77 1 0.6280 0.7963 0.54 0.46 0.00
#> 2nd-C88_S84 1 0.6280 0.7963 0.54 0.46 0.00
#> 2nd-C8_S14 1 0.0000 0.6005 1.00 0.00 0.00
#> 2nd-C93_S88 1 0.6280 0.7963 0.54 0.46 0.00
#> 2nd-C95_S95 1 0.6280 0.7963 0.54 0.46 0.00
#> 3rd-C11_S58 1 0.6280 0.7963 0.54 0.46 0.00
#> 3rd-C12_S68 1 0.0000 0.6005 1.00 0.00 0.00
#> 3rd-C18_S80 2 0.6280 0.7530 0.00 0.54 0.46
#> 3rd-C1_S39 2 0.6280 0.7530 0.00 0.54 0.46
#> 3rd-C20_S22 2 0.6280 0.7530 0.00 0.54 0.46
#> 3rd-C21_S11 2 0.6280 0.3078 0.46 0.54 0.00
#> 3rd-C26_S28 3 0.6280 0.3760 0.46 0.00 0.54
#> 3rd-C27_S49 2 0.6280 0.3078 0.46 0.54 0.00
#> 3rd-C33_S50 1 0.6280 0.7963 0.54 0.46 0.00
#> 3rd-C35_S23 3 0.8853 0.3061 0.14 0.32 0.54
#> 3rd-C36_S2 1 0.6280 0.7963 0.54 0.46 0.00
#> 3rd-C40_S57 2 0.8985 0.5747 0.16 0.54 0.30
#> 3rd-C42_S74 3 0.0000 0.7287 0.00 0.00 1.00
#> 3rd-C46_S93 2 0.6280 0.7530 0.00 0.54 0.46
#> 3rd-C47_S35 1 0.0000 0.6005 1.00 0.00 0.00
#> 3rd-C49_S60 1 0.0000 0.6005 1.00 0.00 0.00
#> 3rd-C4_S25 1 0.6280 0.7963 0.54 0.46 0.00
#> 3rd-C53_S67 1 0.5397 0.7188 0.72 0.28 0.00
#> 3rd-C57_S5 1 0.0000 0.6005 1.00 0.00 0.00
#> 3rd-C58_S3 1 0.6280 0.7963 0.54 0.46 0.00
#> 3rd-C59_S91 1 0.6280 0.7963 0.54 0.46 0.00
#> 3rd-C65_S20 1 0.6280 0.7963 0.54 0.46 0.00
#> 3rd-C67_S69 1 0.6302 -0.3964 0.52 0.48 0.00
#> 3rd-C68_S13 2 0.6280 0.7530 0.00 0.54 0.46
#> 3rd-C6_S44 1 0.6280 0.7963 0.54 0.46 0.00
#> 3rd-C71_S80 1 0.6280 0.7963 0.54 0.46 0.00
#> 3rd-C76_S22 2 0.6280 0.7530 0.00 0.54 0.46
#> 3rd-C79_S67 1 0.0000 0.6005 1.00 0.00 0.00
#> 3rd-C82_S11 1 0.6280 0.7963 0.54 0.46 0.00
#> 3rd-C84_S75 1 0.6280 0.7963 0.54 0.46 0.00
#> 3rd-C85_S79 1 0.0000 0.6005 1.00 0.00 0.00
#> 3rd-C86_S85 2 0.6280 0.7530 0.00 0.54 0.46
#> 3rd-C87_S88 2 0.6280 0.7530 0.00 0.54 0.46
#> 3rd-C88_S24 1 0.6280 0.7963 0.54 0.46 0.00
#> 3rd-C91_S91 1 0.0000 0.6005 1.00 0.00 0.00
#> 3rd-C92_S86 1 0.6280 0.7963 0.54 0.46 0.00
#> 3rd-C95_S81 1 0.0000 0.6005 1.00 0.00 0.00
#> 3rd-C9_S5 1 0.0000 0.6005 1.00 0.00 0.00
#> 4th-61_S28 1 0.6280 0.7963 0.54 0.46 0.00
#> 4th-C12_S19 2 0.6280 0.3078 0.46 0.54 0.00
#> 4th-C14_S26 1 0.6280 0.7963 0.54 0.46 0.00
#> 4th-C18_S31 1 0.1529 0.5538 0.96 0.04 0.00
#> 4th-C23_S44 2 0.6280 0.7530 0.00 0.54 0.46
#> 4th-C24_S43 3 0.6280 0.1827 0.00 0.46 0.54
#> 4th-C26_S50 1 0.6280 0.7963 0.54 0.46 0.00
#> 4th-C28_S55 2 0.3686 0.2994 0.00 0.86 0.14
#> 4th-C29_S56 2 0.6280 0.7530 0.00 0.54 0.46
#> 4th-C32_S62 2 0.6280 0.7530 0.00 0.54 0.46
#> 4th-C33_S63 2 0.7029 0.3231 0.44 0.54 0.02
#> 4th-C36_S69 1 0.0000 0.6005 1.00 0.00 0.00
#> 4th-C40_S79 1 0.0000 0.6005 1.00 0.00 0.00
#> 4th-C43_S85 2 0.6280 0.7530 0.00 0.54 0.46
#> 4th-C49_S4 2 0.6280 0.7530 0.00 0.54 0.46
#> 4th-C4_S9 1 0.0000 0.6005 1.00 0.00 0.00
#> 4th-C51_S6 2 0.7059 0.2845 0.46 0.52 0.02
#> 4th-C56_S17 1 0.0000 0.6005 1.00 0.00 0.00
#> 4th-C59_S23 2 0.6280 0.3078 0.46 0.54 0.00
#> 4th-C5_S8 1 0.6280 0.7963 0.54 0.46 0.00
#> 4th-C62_S29 1 0.0000 0.6005 1.00 0.00 0.00
#> 4th-C63_S30 2 0.6280 0.7530 0.00 0.54 0.46
#> 4th-C64_S34 1 0.0000 0.6005 1.00 0.00 0.00
#> 4th-C66_S36 1 0.0000 0.6005 1.00 0.00 0.00
#> 4th-C67_S40 1 0.6280 0.7963 0.54 0.46 0.00
#> 4th-C69_S42 2 0.6280 0.7530 0.00 0.54 0.46
#> 4th-C70_S46 2 0.6280 0.7530 0.00 0.54 0.46
#> 4th-C73_S54 1 0.0000 0.6005 1.00 0.00 0.00
#> 4th-C75_S52 1 0.0000 0.6005 1.00 0.00 0.00
#> 4th-C78_S58 3 0.0000 0.7287 0.00 0.00 1.00
#> 4th-C79_S66 1 0.0000 0.6005 1.00 0.00 0.00
#> 4th-C7_S15 1 0.6280 0.7963 0.54 0.46 0.00
#> 4th-C80_S65 1 0.0000 0.6005 1.00 0.00 0.00
#> 4th-C81_S64 3 0.0000 0.7287 0.00 0.00 1.00
#> 4th-C82_S72 1 0.0000 0.6005 1.00 0.00 0.00
#> 4th-C83_S71 1 0.0000 0.6005 1.00 0.00 0.00
#> 4th-C85_S78 1 0.6126 0.7712 0.60 0.40 0.00
#> 4th-C86_S77 1 0.0000 0.6005 1.00 0.00 0.00
#> 4th-C87_S76 2 0.6280 0.7530 0.00 0.54 0.46
#> 4th-C88_S84 1 0.0000 0.6005 1.00 0.00 0.00
#> 4th-C89_S83 1 0.6280 0.7963 0.54 0.46 0.00
#> 4th-C8_S14 2 0.6045 0.6448 0.00 0.62 0.38
#> 4th-C92_S89 1 0.6280 -0.3582 0.54 0.46 0.00
#> 4th-C94_S96 1 0.0000 0.6005 1.00 0.00 0.00
#> 4th-C95_S95 3 0.0000 0.7287 0.00 0.00 1.00
#> 4th-C96_S94 1 0.0000 0.6005 1.00 0.00 0.00
#> 5th-C12_S90 2 0.6280 0.7530 0.00 0.54 0.46
#> 5th-C19_S104 3 0.0000 0.7287 0.00 0.00 1.00
#> 5th-C21_S102 3 0.6280 0.3760 0.46 0.00 0.54
#> 5th-C30_S105 3 0.0000 0.7287 0.00 0.00 1.00
#> 5th-C34_S108 3 0.6280 0.3760 0.46 0.00 0.54
#> 5th-C35_S109 1 0.0892 0.6084 0.98 0.02 0.00
#> 5th-C47_S118 3 0.6192 -0.5336 0.00 0.42 0.58
#> 5th-C49_S89 1 0.6280 0.7963 0.54 0.46 0.00
#> 5th-C50_S90 3 0.0000 0.7287 0.00 0.00 1.00
#> 5th-C54_S89 3 0.0000 0.7287 0.00 0.00 1.00
#> 5th-C57_S96 3 0.0000 0.7287 0.00 0.00 1.00
#> 5th-C59_S94 3 0.0000 0.7287 0.00 0.00 1.00
#> 5th-C5_S85 1 0.6280 0.7963 0.54 0.46 0.00
#> 5th-C64_S99 3 0.0000 0.7287 0.00 0.00 1.00
#> 5th-C66_S101 3 0.0000 0.7287 0.00 0.00 1.00
#> 5th-C68_S106 3 0.0000 0.7287 0.00 0.00 1.00
#> 5th-C69_S107 3 0.0000 0.7287 0.00 0.00 1.00
#> 5th-C74_S110 3 0.4291 0.3166 0.00 0.18 0.82
#> 5th-C77_S107 3 0.0000 0.7287 0.00 0.00 1.00
#> 5th-C7_S93 1 0.6280 0.7963 0.54 0.46 0.00
#> 5th-C90_S115 3 0.6280 0.1827 0.00 0.46 0.54
#> 5th-C92_S124 3 0.0000 0.7287 0.00 0.00 1.00
#> 5th-C9_S92 1 0.0892 0.5797 0.98 0.00 0.02
#> 6th-C12_S18 1 0.6280 0.7963 0.54 0.46 0.00
#> 6th-C16_S29 2 0.6045 0.6451 0.00 0.62 0.38
#> 6th-C20_S34 1 0.6280 0.7963 0.54 0.46 0.00
#> 6th-C21_S33 1 0.6244 -0.3159 0.56 0.44 0.00
#> 6th-C22_S39 1 0.6280 0.7963 0.54 0.46 0.00
#> 6th-C23_S38 1 0.6280 0.7963 0.54 0.46 0.00
#> 6th-C24_S37 1 0.6280 0.7963 0.54 0.46 0.00
#> 6th-C29_S50 1 0.6280 0.7963 0.54 0.46 0.00
#> 6th-C2_S2 1 0.6280 0.7963 0.54 0.46 0.00
#> 6th-C30_S51 1 0.6280 0.7963 0.54 0.46 0.00
#> 6th-C40_S73 1 0.6280 0.7963 0.54 0.46 0.00
#> 6th-C42_S75 2 0.2537 0.0178 0.08 0.92 0.00
#> 6th-C51_S6 1 0.6280 0.7963 0.54 0.46 0.00
#> 6th-C53_S10 2 0.6280 0.7530 0.00 0.54 0.46
#> 6th-C54_S11 1 0.6280 0.7963 0.54 0.46 0.00
#> 6th-C59_S21 1 0.6280 0.7963 0.54 0.46 0.00
#> 6th-C5_S8 2 0.7029 0.3238 0.44 0.54 0.02
#> 6th-C63_S26 1 0.6280 0.7963 0.54 0.46 0.00
#> 6th-C65_S31 2 0.6280 0.3078 0.46 0.54 0.00
#> 6th-C66_S32 1 0.6280 0.7963 0.54 0.46 0.00
#> 6th-C71_S41 1 0.6280 0.7963 0.54 0.46 0.00
#> 6th-C73_S48 1 0.6280 0.7963 0.54 0.46 0.00
#> 6th-C75_S46 1 0.6280 0.7963 0.54 0.46 0.00
#> 6th-C77_S53 1 0.6280 0.7963 0.54 0.46 0.00
#> 6th-C79_S60 1 0.6280 0.7963 0.54 0.46 0.00
#> 6th-C80_S59 1 0.6280 0.7963 0.54 0.46 0.00
#> 6th-C85_S72 1 0.6280 0.7963 0.54 0.46 0.00
#> 6th-C87_S70 3 0.6280 0.3760 0.46 0.00 0.54
#> 6th-C91_S84 2 0.6280 0.7530 0.00 0.54 0.46
#> 6th-C93_S82 2 0.2537 0.2284 0.00 0.92 0.08
#> 7th-C10_S19 1 0.6280 0.7963 0.54 0.46 0.00
#> 7th-C11_S18 1 0.0000 0.6005 1.00 0.00 0.00
#> 7th-C14_S24 1 0.0000 0.6005 1.00 0.00 0.00
#> 7th-C15_S23 2 0.6280 0.7530 0.00 0.54 0.46
#> 7th-C17_S29 2 0.6280 0.7530 0.00 0.54 0.46
#> 7th-C24_S40 1 0.4291 0.3361 0.82 0.18 0.00
#> 7th-C25_S43 1 0.6280 0.7963 0.54 0.46 0.00
#> 7th-C31_S53 1 0.6280 0.7963 0.54 0.46 0.00
#> 7th-C32_S54 2 0.8853 0.4143 0.32 0.54 0.14
#> 7th-C34_S59 1 0.9583 -0.3333 0.48 0.26 0.26
#> 7th-C36_S61 1 0.0000 0.6005 1.00 0.00 0.00
#> 7th-C40_S70 3 0.0000 0.7287 0.00 0.00 1.00
#> 7th-C44_S76 2 0.6280 0.7530 0.00 0.54 0.46
#> 7th-C45_S77 1 0.6280 0.7963 0.54 0.46 0.00
#> 7th-C50_S5 1 0.6280 0.7963 0.54 0.46 0.00
#> 7th-C53_S10 1 0.6280 0.7963 0.54 0.46 0.00
#> 7th-C56_S15 2 0.6280 0.7530 0.00 0.54 0.46
#> 7th-C58_S20 1 0.0000 0.6005 1.00 0.00 0.00
#> 7th-C59_S21 1 0.6280 0.7963 0.54 0.46 0.00
#> 7th-C62_S27 1 0.6280 0.7963 0.54 0.46 0.00
#> 7th-C64_S31 1 0.6280 0.7963 0.54 0.46 0.00
#> 7th-C66_S33 1 0.6280 0.7963 0.54 0.46 0.00
#> 7th-C68_S38 2 0.6280 0.7530 0.00 0.54 0.46
#> 7th-C69_S39 2 0.6280 0.7530 0.00 0.54 0.46
#> 7th-C72_S42 2 0.6924 0.6889 0.02 0.58 0.40
#> 7th-C73_S47 1 0.6280 0.7963 0.54 0.46 0.00
#> 7th-C77_S51 1 0.6280 0.7963 0.54 0.46 0.00
#> 7th-C79_S58 1 0.0000 0.6005 1.00 0.00 0.00
#> 7th-C80_S57 1 0.6280 0.7963 0.54 0.46 0.00
#> 7th-C82_S64 1 0.6280 0.7963 0.54 0.46 0.00
#> 7th-C84_S62 1 0.6280 0.7963 0.54 0.46 0.00
#> 7th-C88_S75 2 0.6280 0.7530 0.00 0.54 0.46
#> 7th-C89_S74 1 0.6280 0.7963 0.54 0.46 0.00
#> 7th-C8_S13 1 0.6280 0.7963 0.54 0.46 0.00
#> 7th-C90_S73 1 0.6280 0.7963 0.54 0.46 0.00
#> 7th-C96_S82 1 0.6280 0.7963 0.54 0.46 0.00
#> 8th-C10_S100 1 0.6280 0.7963 0.54 0.46 0.00
#> 8th-C11_S99 2 0.7029 0.3238 0.44 0.54 0.02
#> 8th-C20_S116 2 0.6280 0.7530 0.00 0.54 0.46
#> 8th-C24_S120 1 0.6280 0.7963 0.54 0.46 0.00
#> 8th-C2_S85 1 0.6280 0.7963 0.54 0.46 0.00
#> 8th-C34_S141 2 0.6280 0.7530 0.00 0.54 0.46
#> 8th-C44_S155 1 0.6280 0.7963 0.54 0.46 0.00
#> 8th-C55_S96 1 0.6309 -0.4326 0.50 0.50 0.00
#> 8th-C57_S98 1 0.2959 0.4701 0.90 0.10 0.00
#> 8th-C58_S101 1 0.6192 -0.2708 0.58 0.42 0.00
#> 8th-C59_S102 2 0.8215 0.3662 0.38 0.54 0.08
#> 8th-C61_S107 2 0.6280 0.7530 0.00 0.54 0.46
#> 8th-C64_S112 2 0.6280 0.7530 0.00 0.54 0.46
#> 8th-C65_S113 2 0.6192 -0.7048 0.42 0.58 0.00
#> 8th-C67_S117 3 0.8853 0.3061 0.14 0.32 0.54
#> 8th-C6_S88 2 0.6280 0.7530 0.00 0.54 0.46
#> 8th-C73_S130 3 0.0000 0.7287 0.00 0.00 1.00
#> 8th-C74_S129 1 0.0000 0.6005 1.00 0.00 0.00
#> 8th-C7_S95 2 0.6280 0.7530 0.00 0.54 0.46
#> 8th-C85_S150 1 0.0000 0.6005 1.00 0.00 0.00
#> 8th-C87_S148 1 0.6280 0.7963 0.54 0.46 0.00
#> 8th-C92_S157 2 0.6280 0.7530 0.00 0.54 0.46
#> 8th-C95_S161 2 0.6280 0.7530 0.00 0.54 0.46
#> 9th-C10_S18 1 0.6280 0.7963 0.54 0.46 0.00
#> 9th-C11_S17 1 0.6280 0.7963 0.54 0.46 0.00
#> 9th-C15_S22 2 0.6280 0.7530 0.00 0.54 0.46
#> 9th-C16_S30 2 0.6280 0.7530 0.00 0.54 0.46
#> 9th-C17_S29 2 0.6280 0.7530 0.00 0.54 0.46
#> 9th-C19_S36 2 0.6280 0.7530 0.00 0.54 0.46
#> 9th-C1_S3 1 0.6280 0.7963 0.54 0.46 0.00
#> 9th-C28_S50 2 0.6280 0.7530 0.00 0.54 0.46
#> 9th-C29_S51 2 0.8472 0.6440 0.10 0.54 0.36
#> 9th-C30_S52 2 0.7029 0.3238 0.44 0.54 0.02
#> 9th-C36_S59 3 0.0000 0.7287 0.00 0.00 1.00
#> 9th-C38_S64 1 0.6280 0.7963 0.54 0.46 0.00
#> 9th-C3_S1 1 0.6280 0.7963 0.54 0.46 0.00
#> 9th-C40_S69 2 0.6280 0.7530 0.00 0.54 0.46
#> 9th-C41_S70 1 0.6280 0.7963 0.54 0.46 0.00
#> 9th-C46_S79 1 0.6280 0.7963 0.54 0.46 0.00
#> 9th-C57_S16 1 0.4035 0.4511 0.88 0.04 0.08
#> 9th-C5_S8 2 0.7901 0.6892 0.06 0.54 0.40
#> 9th-C61_S25 3 0.0000 0.7287 0.00 0.00 1.00
#> 9th-C62_S26 2 0.7029 0.3238 0.44 0.54 0.02
#> 9th-C64_S31 2 0.6280 0.7530 0.00 0.54 0.46
#> 9th-C65_S32 2 0.6280 0.7530 0.00 0.54 0.46
#> 9th-C66_S33 2 0.6280 0.7530 0.00 0.54 0.46
#> 9th-C67_S37 2 0.6280 0.7530 0.00 0.54 0.46
#> 9th-C6_S7 2 0.9602 -0.6375 0.32 0.46 0.22
#> 9th-C70_S42 1 0.6280 0.7963 0.54 0.46 0.00
#> 9th-C74_S48 2 0.6280 0.3078 0.46 0.54 0.00
#> 9th-C77_S53 2 0.7029 0.3238 0.44 0.54 0.02
#> 9th-C80_S56 1 0.0000 0.6005 1.00 0.00 0.00
#> 9th-C81_S55 1 0.6280 0.7963 0.54 0.46 0.00
#> 9th-C83_S61 1 0.0000 0.6005 1.00 0.00 0.00
#> 9th-C84_S60 3 0.6302 -0.6585 0.00 0.48 0.52
#> 9th-C86_S67 1 0.6280 0.7963 0.54 0.46 0.00
#> 9th-C89_S72 1 0.6280 0.7963 0.54 0.46 0.00
#> 9th-C8_S14 1 0.6280 0.7963 0.54 0.46 0.00
#> 9th-C93_S76 1 0.6280 0.7963 0.54 0.46 0.00
#> 9th-C96_S81 3 0.0000 0.7287 0.00 0.00 1.00
#> 9th-C9_S13 1 0.5216 0.1794 0.74 0.26 0.00
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> 10th_C10_S104 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 10th_C13_S61 1 0.0000 0.9650 1.00 0.00 0.00 0.00
#> 10th_C14_S53 2 0.1211 0.9479 0.04 0.96 0.00 0.00
#> 10th_C16_S105 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 10th_C19_S62 3 0.0000 0.9822 0.00 0.00 1.00 0.00
#> 10th_C1_S59 2 0.0707 0.9632 0.02 0.98 0.00 0.00
#> 10th_C20_S54 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 10th_C23_S98 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 10th_C24_S90 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 10th_C30_S107 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 10th_C31_S48 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 10th_C41_S101 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 10th_C45_S66 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 10th_C46_S94 3 0.0000 0.9822 0.00 0.00 1.00 0.00
#> 10th_C4_S103 3 0.0000 0.9822 0.00 0.00 1.00 0.00
#> 10th_C54_S124 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 10th_C56_S74 3 0.0000 0.9822 0.00 0.00 1.00 0.00
#> 10th_C68_S75 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 10th_C73_S84 3 0.0000 0.9822 0.00 0.00 1.00 0.00
#> 10th_C74_S76 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 10th_C76_S128 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 10th_C7_S60 3 0.0000 0.9822 0.00 0.00 1.00 0.00
#> 10th_C81_S70 1 0.0000 0.9650 1.00 0.00 0.00 0.00
#> 10th_C84_S115 1 0.0000 0.9650 1.00 0.00 0.00 0.00
#> 10th_C85_S86 2 0.0707 0.9632 0.02 0.98 0.00 0.00
#> 10th_C88_S130 3 0.0000 0.9822 0.00 0.00 1.00 0.00
#> 10th_C8_S52 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 10th_C90_S116 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 10th_C96_S117 4 0.1211 0.9075 0.00 0.04 0.00 0.96
#> 11th-C16_S64 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 11th-C24_S49 3 0.0000 0.9822 0.00 0.00 1.00 0.00
#> 11th-C33_S20 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 11th-C36_S67 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 11th-C39_S21 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 11th-C40_S52 3 0.0000 0.9822 0.00 0.00 1.00 0.00
#> 11th-C41_S60 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 11th-C44_S15 1 0.0000 0.9650 1.00 0.00 0.00 0.00
#> 11th-C49_S23 1 0.0707 0.9717 0.98 0.00 0.00 0.02
#> 11th-C51_S39 1 0.0000 0.9650 1.00 0.00 0.00 0.00
#> 11th-C53_S78 1 0.0000 0.9650 1.00 0.00 0.00 0.00
#> 11th-C58_S71 3 0.0000 0.9822 0.00 0.00 1.00 0.00
#> 11th-C5_S54 2 0.3172 0.7989 0.00 0.84 0.00 0.16
#> 11th-C61_S25 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 11th-C66_S88 1 0.0000 0.9650 1.00 0.00 0.00 0.00
#> 11th-C68_S34 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 11th-C7_S16 3 0.0000 0.9822 0.00 0.00 1.00 0.00
#> 12th-C11_S147 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 12th-C12_S139 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 12th-C14_S190 1 0.0000 0.9650 1.00 0.00 0.00 0.00
#> 12th-C20_S191 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 12th-C24_S141 1 0.0000 0.9650 1.00 0.00 0.00 0.00
#> 12th-C25_S185 2 0.1211 0.9479 0.04 0.96 0.00 0.00
#> 12th-C26_S192 2 0.1211 0.9479 0.04 0.96 0.00 0.00
#> 12th-C28_S142 4 0.4406 0.6101 0.00 0.30 0.00 0.70
#> 12th-C29_S150 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 12th-C30_S157 2 0.1211 0.9479 0.04 0.96 0.00 0.00
#> 12th-C33_S200 2 0.2345 0.8805 0.10 0.90 0.00 0.00
#> 12th-C42_S159 1 0.0000 0.9650 1.00 0.00 0.00 0.00
#> 12th-C46_S145 3 0.0000 0.9822 0.00 0.00 1.00 0.00
#> 12th-C48_S160 2 0.0707 0.9632 0.02 0.98 0.00 0.00
#> 12th-C51_S217 2 0.0707 0.9632 0.02 0.98 0.00 0.00
#> 12th-C55_S203 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 12th-C58_S162 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 12th-C59_S169 1 0.0000 0.9650 1.00 0.00 0.00 0.00
#> 12th-C60_S176 1 0.0707 0.9717 0.98 0.00 0.00 0.02
#> 12th-C63_S219 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 12th-C64_S163 1 0.0000 0.9650 1.00 0.00 0.00 0.00
#> 12th-C65_S170 1 0.0707 0.9717 0.98 0.00 0.00 0.02
#> 12th-C69_S135 3 0.0707 0.9634 0.00 0.02 0.98 0.00
#> 12th-C74_S214 1 0.0000 0.9650 1.00 0.00 0.00 0.00
#> 12th-C76_S177 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 12th-C7_S196 1 0.0000 0.9650 1.00 0.00 0.00 0.00
#> 12th-C80_S215 3 0.2011 0.9023 0.00 0.08 0.92 0.00
#> 12th-C81_S207 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 12th-C84_S165 1 0.0000 0.9650 1.00 0.00 0.00 0.00
#> 12th-C85_S137 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 12th-C90_S166 1 0.0000 0.9650 1.00 0.00 0.00 0.00
#> 12th-C94_S180 3 0.0000 0.9822 0.00 0.00 1.00 0.00
#> 12th-C95_S174 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 12th-C96_S167 1 0.0707 0.9717 0.98 0.00 0.00 0.02
#> 13th_C12_S178 2 0.2345 0.8825 0.10 0.90 0.00 0.00
#> 13th_C13_S149 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 13th_C16_S193 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 13th_C23_S187 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 13th_C34_S181 1 0.0000 0.9650 1.00 0.00 0.00 0.00
#> 13th_C39_S153 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 13th_C60_S213 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 13th_C66_S214 4 0.3400 0.7387 0.18 0.00 0.00 0.82
#> 13th_C76_S216 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 13th_C94_S219 2 0.1211 0.9479 0.04 0.96 0.00 0.00
#> 13th_C96_S204 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 1st-61_S27 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 1st-C11_S58 1 0.0000 0.9650 1.00 0.00 0.00 0.00
#> 1st-C19_S20 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 1st-C21_S4 4 0.1211 0.9075 0.00 0.04 0.00 0.96
#> 1st-C32_S14 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 1st-C34_S54 3 0.0000 0.9822 0.00 0.00 1.00 0.00
#> 1st-C42_S71 3 0.0000 0.9822 0.00 0.00 1.00 0.00
#> 1st-C50_S33 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 1st-C56_S34 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 1st-C57_S42 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 1st-C58_S76 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 1st-C64_S79 1 0.0707 0.9717 0.98 0.00 0.00 0.02
#> 1st-C68_S36 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 1st-C69_S44 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 1st-C71_S83 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 1st-C73_S45 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 1st-C75_S29 1 0.3801 0.7625 0.78 0.00 0.00 0.22
#> 1st-C77_S86 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 1st-C78_S85 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 1st-C80_S38 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 1st-C90_S91 1 0.0707 0.9717 0.98 0.00 0.00 0.02
#> 2nd-C11_S20 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 2nd-C15_S25 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 2nd-C16_S33 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 2nd-C17_S32 1 0.0707 0.9717 0.98 0.00 0.00 0.02
#> 2nd-C21_S37 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 2nd-C25_S49 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 2nd-C26_S50 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 2nd-C29_S56 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 2nd-C31_S61 4 0.1211 0.9075 0.00 0.04 0.00 0.96
#> 2nd-C32_S62 1 0.0707 0.9717 0.98 0.00 0.00 0.02
#> 2nd-C38_S74 1 0.0707 0.9717 0.98 0.00 0.00 0.02
#> 2nd-C39_S75 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 2nd-C47_S92 4 0.2011 0.8740 0.00 0.08 0.00 0.92
#> 2nd-C54_S12 3 0.0000 0.9822 0.00 0.00 1.00 0.00
#> 2nd-C57_S18 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 2nd-C62_S29 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 2nd-C67_S40 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 2nd-C6_S7 2 0.3801 0.7014 0.00 0.78 0.00 0.22
#> 2nd-C72_S48 1 0.0707 0.9501 0.98 0.02 0.00 0.00
#> 2nd-C74_S53 4 0.5000 0.0762 0.00 0.50 0.00 0.50
#> 2nd-C75_S52 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 2nd-C76_S60 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 2nd-C77_S59 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 2nd-C80_S65 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 2nd-C81_S64 2 0.0707 0.9632 0.02 0.98 0.00 0.00
#> 2nd-C83_S71 4 0.1211 0.9054 0.00 0.00 0.04 0.96
#> 2nd-C86_S77 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 2nd-C88_S84 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 2nd-C8_S14 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 2nd-C93_S88 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 2nd-C95_S95 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 3rd-C11_S58 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 3rd-C12_S68 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 3rd-C18_S80 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 3rd-C1_S39 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 3rd-C20_S22 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 3rd-C21_S11 4 0.4624 0.5319 0.00 0.34 0.00 0.66
#> 3rd-C26_S28 4 0.1211 0.9054 0.00 0.00 0.04 0.96
#> 3rd-C27_S49 4 0.1211 0.9075 0.00 0.04 0.00 0.96
#> 3rd-C33_S50 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 3rd-C35_S23 3 0.0000 0.9822 0.00 0.00 1.00 0.00
#> 3rd-C36_S2 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 3rd-C40_S57 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 3rd-C42_S74 3 0.0000 0.9822 0.00 0.00 1.00 0.00
#> 3rd-C46_S93 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 3rd-C47_S35 4 0.0707 0.9192 0.02 0.00 0.00 0.98
#> 3rd-C49_S60 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 3rd-C4_S25 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 3rd-C53_S67 1 0.4948 0.2915 0.56 0.00 0.00 0.44
#> 3rd-C57_S5 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 3rd-C58_S3 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 3rd-C59_S91 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 3rd-C65_S20 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 3rd-C67_S69 4 0.0707 0.9241 0.00 0.02 0.00 0.98
#> 3rd-C68_S13 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 3rd-C6_S44 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 3rd-C71_S80 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 3rd-C76_S22 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 3rd-C79_S67 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 3rd-C82_S11 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 3rd-C84_S75 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 3rd-C85_S79 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 3rd-C86_S85 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 3rd-C87_S88 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 3rd-C88_S24 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 3rd-C91_S91 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 3rd-C92_S86 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 3rd-C95_S81 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 3rd-C9_S5 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 4th-61_S28 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 4th-C12_S19 4 0.1211 0.9075 0.00 0.04 0.00 0.96
#> 4th-C14_S26 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 4th-C18_S31 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 4th-C23_S44 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 4th-C24_S43 3 0.0000 0.9822 0.00 0.00 1.00 0.00
#> 4th-C26_S50 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 4th-C28_S55 2 0.1211 0.9479 0.04 0.96 0.00 0.00
#> 4th-C29_S56 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 4th-C32_S62 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 4th-C33_S63 4 0.4624 0.5326 0.00 0.34 0.00 0.66
#> 4th-C36_S69 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 4th-C40_S79 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 4th-C43_S85 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 4th-C49_S4 2 0.0707 0.9632 0.02 0.98 0.00 0.00
#> 4th-C4_S9 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 4th-C51_S6 4 0.1211 0.9075 0.00 0.04 0.00 0.96
#> 4th-C56_S17 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 4th-C59_S23 4 0.3801 0.7272 0.00 0.22 0.00 0.78
#> 4th-C5_S8 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 4th-C62_S29 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 4th-C63_S30 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 4th-C64_S34 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 4th-C66_S36 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 4th-C67_S40 1 0.0707 0.9717 0.98 0.00 0.00 0.02
#> 4th-C69_S42 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 4th-C70_S46 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 4th-C73_S54 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 4th-C75_S52 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 4th-C78_S58 3 0.0000 0.9822 0.00 0.00 1.00 0.00
#> 4th-C79_S66 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 4th-C7_S15 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 4th-C80_S65 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 4th-C81_S64 3 0.0000 0.9822 0.00 0.00 1.00 0.00
#> 4th-C82_S72 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 4th-C83_S71 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 4th-C85_S78 1 0.4406 0.6268 0.70 0.00 0.00 0.30
#> 4th-C86_S77 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 4th-C87_S76 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 4th-C88_S84 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 4th-C89_S83 1 0.0000 0.9650 1.00 0.00 0.00 0.00
#> 4th-C8_S14 2 0.1211 0.9479 0.04 0.96 0.00 0.00
#> 4th-C92_S89 4 0.0707 0.9241 0.00 0.02 0.00 0.98
#> 4th-C94_S96 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 4th-C95_S95 3 0.0000 0.9822 0.00 0.00 1.00 0.00
#> 4th-C96_S94 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 5th-C12_S90 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 5th-C19_S104 3 0.0000 0.9822 0.00 0.00 1.00 0.00
#> 5th-C21_S102 3 0.0000 0.9822 0.00 0.00 1.00 0.00
#> 5th-C30_S105 3 0.0000 0.9822 0.00 0.00 1.00 0.00
#> 5th-C34_S108 3 0.3801 0.7096 0.00 0.00 0.78 0.22
#> 5th-C35_S109 4 0.1211 0.8991 0.04 0.00 0.00 0.96
#> 5th-C47_S118 2 0.4277 0.6131 0.00 0.72 0.28 0.00
#> 5th-C49_S89 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 5th-C50_S90 3 0.0000 0.9822 0.00 0.00 1.00 0.00
#> 5th-C54_S89 3 0.0000 0.9822 0.00 0.00 1.00 0.00
#> 5th-C57_S96 3 0.0000 0.9822 0.00 0.00 1.00 0.00
#> 5th-C59_S94 3 0.0000 0.9822 0.00 0.00 1.00 0.00
#> 5th-C5_S85 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 5th-C64_S99 3 0.0000 0.9822 0.00 0.00 1.00 0.00
#> 5th-C66_S101 3 0.0000 0.9822 0.00 0.00 1.00 0.00
#> 5th-C68_S106 3 0.0000 0.9822 0.00 0.00 1.00 0.00
#> 5th-C69_S107 3 0.0000 0.9822 0.00 0.00 1.00 0.00
#> 5th-C74_S110 3 0.4713 0.4315 0.00 0.36 0.64 0.00
#> 5th-C77_S107 3 0.1637 0.9238 0.00 0.06 0.94 0.00
#> 5th-C7_S93 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 5th-C90_S115 3 0.0000 0.9822 0.00 0.00 1.00 0.00
#> 5th-C92_S124 3 0.0000 0.9822 0.00 0.00 1.00 0.00
#> 5th-C9_S92 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 6th-C12_S18 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 6th-C16_S29 2 0.1211 0.9479 0.04 0.96 0.00 0.00
#> 6th-C20_S34 1 0.0707 0.9717 0.98 0.00 0.00 0.02
#> 6th-C21_S33 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 6th-C22_S39 1 0.0707 0.9717 0.98 0.00 0.00 0.02
#> 6th-C23_S38 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 6th-C24_S37 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 6th-C29_S50 1 0.0707 0.9717 0.98 0.00 0.00 0.02
#> 6th-C2_S2 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 6th-C30_S51 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 6th-C40_S73 1 0.0000 0.9650 1.00 0.00 0.00 0.00
#> 6th-C42_S75 1 0.3801 0.6852 0.78 0.22 0.00 0.00
#> 6th-C51_S6 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 6th-C53_S10 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 6th-C54_S11 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 6th-C59_S21 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 6th-C5_S8 2 0.4406 0.5443 0.00 0.70 0.00 0.30
#> 6th-C63_S26 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 6th-C65_S31 4 0.3975 0.7033 0.00 0.24 0.00 0.76
#> 6th-C66_S32 1 0.0000 0.9650 1.00 0.00 0.00 0.00
#> 6th-C71_S41 1 0.0000 0.9650 1.00 0.00 0.00 0.00
#> 6th-C73_S48 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 6th-C75_S46 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 6th-C77_S53 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 6th-C79_S60 1 0.0000 0.9650 1.00 0.00 0.00 0.00
#> 6th-C80_S59 1 0.0000 0.9650 1.00 0.00 0.00 0.00
#> 6th-C85_S72 1 0.0000 0.9650 1.00 0.00 0.00 0.00
#> 6th-C87_S70 4 0.0707 0.9228 0.00 0.00 0.02 0.98
#> 6th-C91_S84 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 6th-C93_S82 2 0.3400 0.7703 0.18 0.82 0.00 0.00
#> 7th-C10_S19 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 7th-C11_S18 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 7th-C14_S24 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 7th-C15_S23 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 7th-C17_S29 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 7th-C24_S40 4 0.3198 0.8410 0.04 0.08 0.00 0.88
#> 7th-C25_S43 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 7th-C31_S53 1 0.0707 0.9717 0.98 0.00 0.00 0.02
#> 7th-C32_S54 2 0.2011 0.8978 0.00 0.92 0.00 0.08
#> 7th-C34_S59 4 0.0707 0.9228 0.00 0.00 0.02 0.98
#> 7th-C36_S61 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 7th-C40_S70 3 0.0000 0.9822 0.00 0.00 1.00 0.00
#> 7th-C44_S76 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 7th-C45_S77 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 7th-C50_S5 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 7th-C53_S10 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 7th-C56_S15 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 7th-C58_S20 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 7th-C59_S21 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 7th-C62_S27 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 7th-C64_S31 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 7th-C66_S33 1 0.0000 0.9650 1.00 0.00 0.00 0.00
#> 7th-C68_S38 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 7th-C69_S39 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 7th-C72_S42 2 0.1211 0.9479 0.04 0.96 0.00 0.00
#> 7th-C73_S47 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 7th-C77_S51 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 7th-C79_S58 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 7th-C80_S57 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 7th-C82_S64 1 0.1211 0.9631 0.96 0.00 0.00 0.04
#> 7th-C84_S62 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 7th-C88_S75 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 7th-C89_S74 1 0.0707 0.9717 0.98 0.00 0.00 0.02
#> 7th-C8_S13 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 7th-C90_S73 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 7th-C96_S82 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 8th-C10_S100 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 8th-C11_S99 4 0.4855 0.3936 0.00 0.40 0.00 0.60
#> 8th-C20_S116 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 8th-C24_S120 1 0.0707 0.9717 0.98 0.00 0.00 0.02
#> 8th-C2_S85 1 0.1211 0.9735 0.96 0.00 0.00 0.04
#> 8th-C34_S141 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 8th-C44_S155 1 0.0000 0.9650 1.00 0.00 0.00 0.00
#> 8th-C55_S96 4 0.0707 0.9241 0.00 0.02 0.00 0.98
#> 8th-C57_S98 4 0.0707 0.9241 0.00 0.02 0.00 0.98
#> 8th-C58_S101 4 0.0707 0.9241 0.00 0.02 0.00 0.98
#> 8th-C59_S102 2 0.4277 0.5866 0.00 0.72 0.00 0.28
#> 8th-C61_S107 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 8th-C64_S112 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 8th-C65_S113 1 0.0000 0.9650 1.00 0.00 0.00 0.00
#> 8th-C67_S117 3 0.0000 0.9822 0.00 0.00 1.00 0.00
#> 8th-C6_S88 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 8th-C73_S130 3 0.0000 0.9822 0.00 0.00 1.00 0.00
#> 8th-C74_S129 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 8th-C7_S95 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 8th-C85_S150 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 8th-C87_S148 1 0.0707 0.9717 0.98 0.00 0.00 0.02
#> 8th-C92_S157 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 8th-C95_S161 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 9th-C10_S18 1 0.0707 0.9717 0.98 0.00 0.00 0.02
#> 9th-C11_S17 1 0.0000 0.9650 1.00 0.00 0.00 0.00
#> 9th-C15_S22 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 9th-C16_S30 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 9th-C17_S29 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 9th-C19_S36 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 9th-C1_S3 1 0.0000 0.9650 1.00 0.00 0.00 0.00
#> 9th-C28_S50 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 9th-C29_S51 2 0.1637 0.9203 0.00 0.94 0.00 0.06
#> 9th-C30_S52 4 0.4134 0.6778 0.00 0.26 0.00 0.74
#> 9th-C36_S59 3 0.0000 0.9822 0.00 0.00 1.00 0.00
#> 9th-C38_S64 1 0.0000 0.9650 1.00 0.00 0.00 0.00
#> 9th-C3_S1 1 0.0000 0.9650 1.00 0.00 0.00 0.00
#> 9th-C40_S69 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 9th-C41_S70 1 0.0000 0.9650 1.00 0.00 0.00 0.00
#> 9th-C46_S79 1 0.0000 0.9650 1.00 0.00 0.00 0.00
#> 9th-C57_S16 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 9th-C5_S8 2 0.0707 0.9596 0.00 0.98 0.00 0.02
#> 9th-C61_S25 3 0.0000 0.9822 0.00 0.00 1.00 0.00
#> 9th-C62_S26 4 0.4948 0.2819 0.00 0.44 0.00 0.56
#> 9th-C64_S31 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 9th-C65_S32 2 0.1211 0.9479 0.04 0.96 0.00 0.00
#> 9th-C66_S33 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 9th-C67_S37 2 0.0000 0.9763 0.00 1.00 0.00 0.00
#> 9th-C6_S7 1 0.0000 0.9650 1.00 0.00 0.00 0.00
#> 9th-C70_S42 1 0.0000 0.9650 1.00 0.00 0.00 0.00
#> 9th-C74_S48 4 0.3801 0.7260 0.00 0.22 0.00 0.78
#> 9th-C77_S53 4 0.4855 0.3923 0.00 0.40 0.00 0.60
#> 9th-C80_S56 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 9th-C81_S55 1 0.0707 0.9717 0.98 0.00 0.00 0.02
#> 9th-C83_S61 4 0.0000 0.9378 0.00 0.00 0.00 1.00
#> 9th-C84_S60 2 0.1211 0.9442 0.00 0.96 0.04 0.00
#> 9th-C86_S67 1 0.0000 0.9650 1.00 0.00 0.00 0.00
#> 9th-C89_S72 1 0.0000 0.9650 1.00 0.00 0.00 0.00
#> 9th-C8_S14 1 0.0000 0.9650 1.00 0.00 0.00 0.00
#> 9th-C93_S76 1 0.0707 0.9717 0.98 0.00 0.00 0.02
#> 9th-C96_S81 3 0.0000 0.9822 0.00 0.00 1.00 0.00
#> 9th-C9_S13 4 0.0000 0.9378 0.00 0.00 0.00 1.00
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
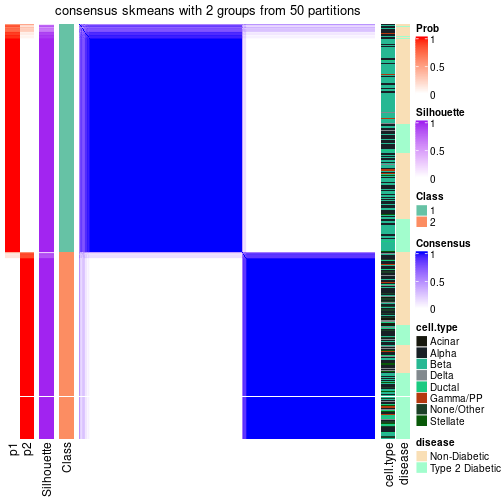
consensus_heatmap(res, k = 3)
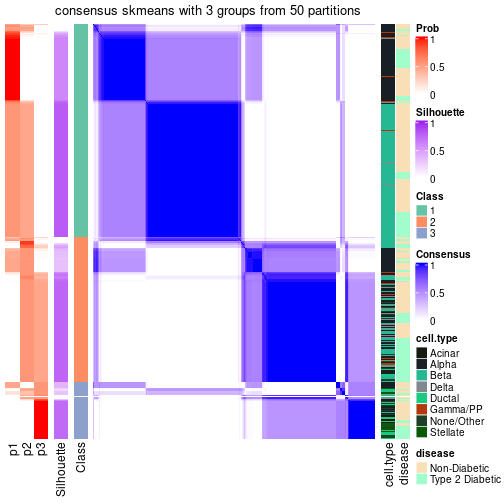
consensus_heatmap(res, k = 4)
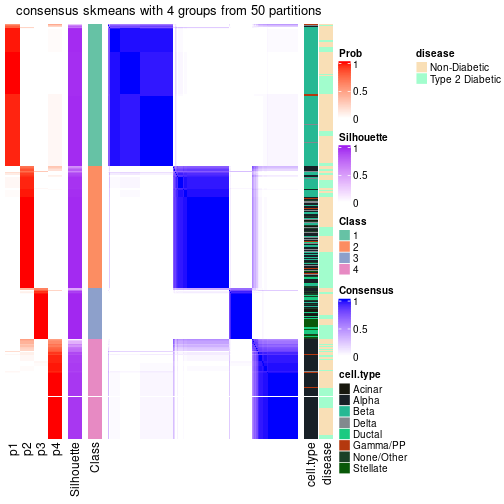
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
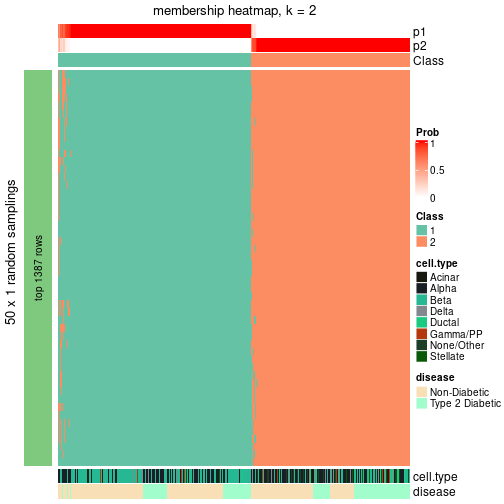
membership_heatmap(res, k = 3)

membership_heatmap(res, k = 4)
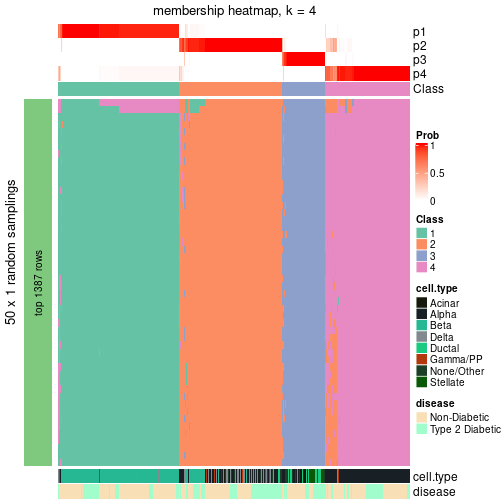
As soon as the classes for columns are determined, the signatures that are significantly different between subgroups can be looked for. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
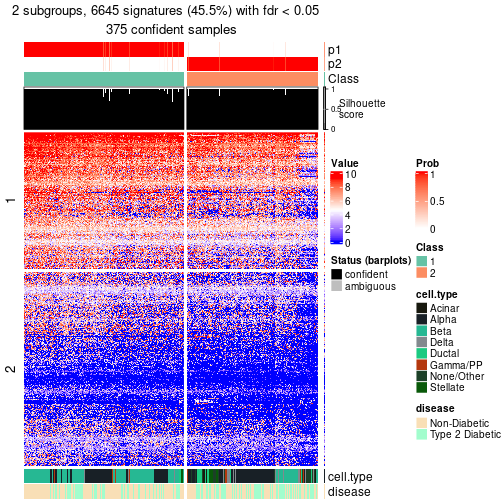
get_signatures(res, k = 3, scale_rows = FALSE)
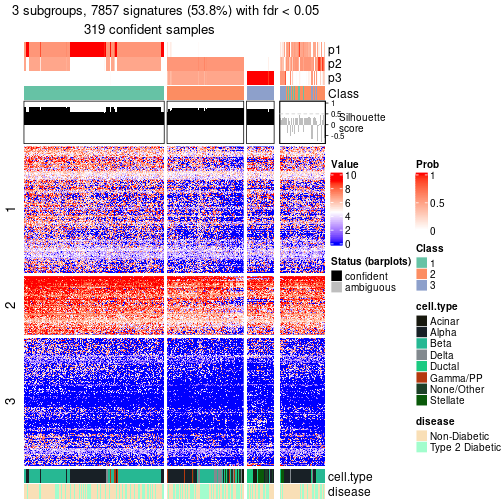
get_signatures(res, k = 4, scale_rows = FALSE)
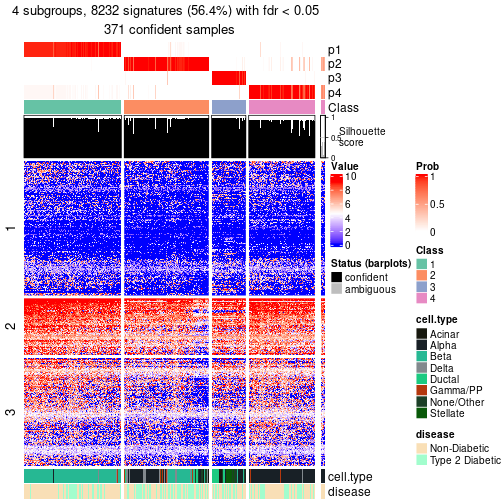
Compare the overlap of signatures from different k:
compare_signatures(res)
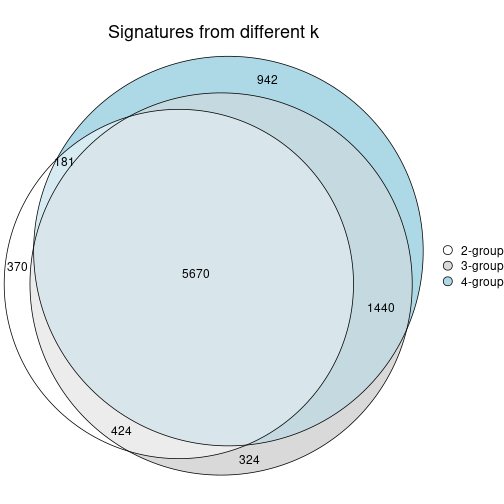
get_signature() returns a data frame invisibly. To get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows (which is done by automatically selecting number of clusters).If there are too many signatures, top_signatures = ... can be set to only show the
signatures with the highest FDRs:
# code only for demonstration
# e.g. to show the top 500 most significant rows
tb = get_signature(res, k = ..., top_signatures = 500)
If the signatures are defined as these which are uniquely high in current group, diff_method argument
can be set to "uniquely_high_in_one_group":
# code only for demonstration
tb = get_signature(res, k = ..., diff_method = "uniquely_high_in_one_group")
UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
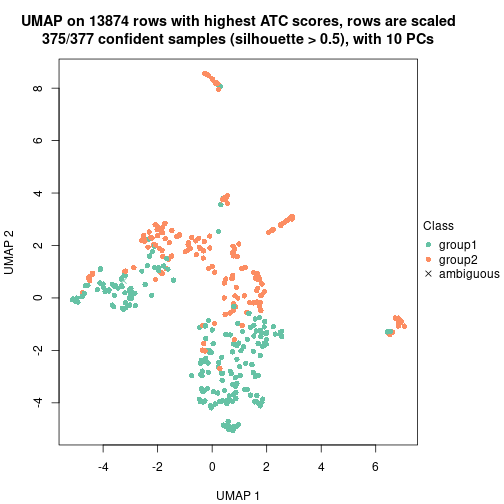
dimension_reduction(res, k = 3, method = "UMAP")
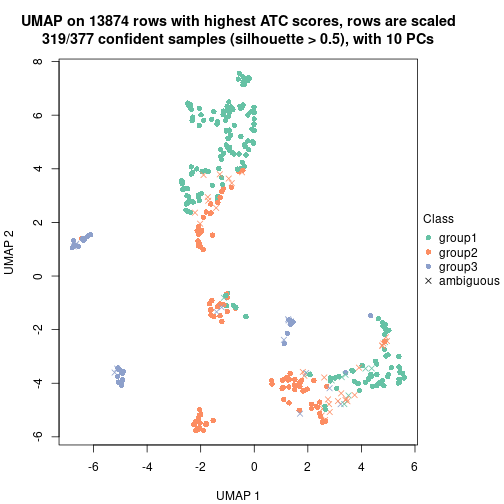
dimension_reduction(res, k = 4, method = "UMAP")
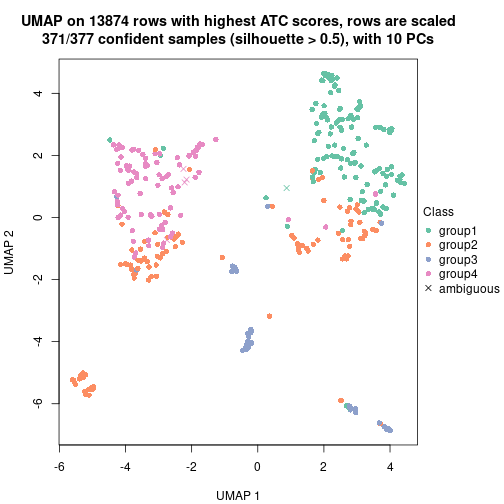
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n_sample cell.type(p-value) disease(p-value) k
#> ATC:skmeans 375 4.18e-17 0.000682 2
#> ATC:skmeans 319 1.26e-37 0.000474 3
#> ATC:skmeans 371 1.24e-89 0.000614 4
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
Parent node: Node01. Child nodes: Node0111 , Node0112 , Node0113 , Node0121-leaf , Node0122 , Node0123 , Node0124-leaf , Node0211-leaf , Node0212-leaf , Node0221-leaf , Node0222-leaf , Node0231-leaf , Node0232-leaf , Node0233-leaf .
The object with results only for a single top-value method and a single partitioning method can be extracted as:
res = res_rh["011"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4.
#> On a matrix with 13873 rows and 207 columns.
#> Top rows (1387) are extracted by 'ATC' method.
#> Subgroups are detected by 'skmeans' method.
#> Performed in total 150 partitions by row resampling.
#> Best k for subgroups seems to be 4.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_partitions"
#> [7] "compare_signatures" "consensus_heatmap" "dimension_reduction"
#> [10] "functional_enrichment" "get_anno_col" "get_anno"
#> [13] "get_classes" "get_consensus" "get_matrix"
#> [16] "get_membership" "get_param" "get_signatures"
#> [19] "get_stats" "is_best_k" "is_stable_k"
#> [22] "membership_heatmap" "ncol" "nrow"
#> [25] "plot_ecdf" "predict_classes" "rownames"
#> [28] "select_partition_number" "show" "suggest_best_k"
#> [31] "test_to_known_factors" "top_rows_heatmap"
collect_plots() function collects all the plots made from res for all k (number of subgroups)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, higher 1-PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 1.000 0.999 0.999 0.483 0.517 0.517
#> 3 3 0.980 0.953 0.980 0.385 0.749 0.543
#> 4 4 0.916 0.899 0.950 0.105 0.868 0.635
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 4
#> attr(,"optional")
#> [1] 2 3
There is also optional best \(k\) = 2 3 that is worth to check.
Following is the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall subgroup
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> 10th_C13_S61 1 0.000 0.999 1.00 0.00
#> 10th_C19_S62 2 0.000 1.000 0.00 1.00
#> 10th_C81_S70 1 0.000 0.999 1.00 0.00
#> 10th_C84_S115 1 0.000 0.999 1.00 0.00
#> 11th-C41_S60 1 0.000 0.999 1.00 0.00
#> 11th-C44_S15 1 0.000 0.999 1.00 0.00
#> 11th-C49_S23 1 0.000 0.999 1.00 0.00
#> 11th-C51_S39 1 0.000 0.999 1.00 0.00
#> 11th-C53_S78 1 0.000 0.999 1.00 0.00
#> 11th-C66_S88 1 0.000 0.999 1.00 0.00
#> 11th-C7_S16 2 0.000 1.000 0.00 1.00
#> 12th-C14_S190 1 0.000 0.999 1.00 0.00
#> 12th-C24_S141 1 0.000 0.999 1.00 0.00
#> 12th-C29_S150 2 0.000 1.000 0.00 1.00
#> 12th-C42_S159 1 0.000 0.999 1.00 0.00
#> 12th-C55_S203 1 0.000 0.999 1.00 0.00
#> 12th-C58_S162 2 0.000 1.000 0.00 1.00
#> 12th-C59_S169 1 0.000 0.999 1.00 0.00
#> 12th-C60_S176 1 0.000 0.999 1.00 0.00
#> 12th-C64_S163 1 0.000 0.999 1.00 0.00
#> 12th-C65_S170 1 0.000 0.999 1.00 0.00
#> 12th-C74_S214 1 0.000 0.999 1.00 0.00
#> 12th-C76_S177 1 0.000 0.999 1.00 0.00
#> 12th-C7_S196 1 0.000 0.999 1.00 0.00
#> 12th-C84_S165 1 0.000 0.999 1.00 0.00
#> 12th-C90_S166 1 0.000 0.999 1.00 0.00
#> 12th-C95_S174 2 0.000 1.000 0.00 1.00
#> 12th-C96_S167 1 0.000 0.999 1.00 0.00
#> 13th_C34_S181 1 0.000 0.999 1.00 0.00
#> 13th_C66_S214 2 0.000 1.000 0.00 1.00
#> 13th_C76_S216 2 0.000 1.000 0.00 1.00
#> 1st-61_S27 1 0.000 0.999 1.00 0.00
#> 1st-C11_S58 1 0.000 0.999 1.00 0.00
#> 1st-C19_S20 2 0.000 1.000 0.00 1.00
#> 1st-C32_S14 1 0.000 0.999 1.00 0.00
#> 1st-C42_S71 2 0.000 1.000 0.00 1.00
#> 1st-C50_S33 2 0.000 1.000 0.00 1.00
#> 1st-C56_S34 2 0.000 1.000 0.00 1.00
#> 1st-C57_S42 2 0.000 1.000 0.00 1.00
#> 1st-C58_S76 1 0.000 0.999 1.00 0.00
#> 1st-C64_S79 1 0.000 0.999 1.00 0.00
#> 1st-C68_S36 2 0.000 1.000 0.00 1.00
#> 1st-C73_S45 2 0.000 1.000 0.00 1.00
#> 1st-C75_S29 2 0.000 1.000 0.00 1.00
#> 1st-C77_S86 2 0.000 1.000 0.00 1.00
#> 1st-C78_S85 2 0.000 1.000 0.00 1.00
#> 1st-C80_S38 2 0.000 1.000 0.00 1.00
#> 1st-C90_S91 1 0.000 0.999 1.00 0.00
#> 2nd-C11_S20 2 0.000 1.000 0.00 1.00
#> 2nd-C15_S25 1 0.000 0.999 1.00 0.00
#> 2nd-C16_S33 2 0.000 1.000 0.00 1.00
#> 2nd-C17_S32 1 0.000 0.999 1.00 0.00
#> 2nd-C21_S37 1 0.000 0.999 1.00 0.00
#> 2nd-C26_S50 2 0.000 1.000 0.00 1.00
#> 2nd-C32_S62 1 0.000 0.999 1.00 0.00
#> 2nd-C38_S74 1 0.000 0.999 1.00 0.00
#> 2nd-C39_S75 2 0.000 1.000 0.00 1.00
#> 2nd-C62_S29 1 0.000 0.999 1.00 0.00
#> 2nd-C67_S40 2 0.000 1.000 0.00 1.00
#> 2nd-C72_S48 1 0.000 0.999 1.00 0.00
#> 2nd-C75_S52 2 0.000 1.000 0.00 1.00
#> 2nd-C77_S59 2 0.000 1.000 0.00 1.00
#> 2nd-C80_S65 2 0.000 1.000 0.00 1.00
#> 2nd-C86_S77 1 0.000 0.999 1.00 0.00
#> 2nd-C88_S84 1 0.000 0.999 1.00 0.00
#> 2nd-C8_S14 2 0.000 1.000 0.00 1.00
#> 2nd-C93_S88 1 0.000 0.999 1.00 0.00
#> 2nd-C95_S95 1 0.000 0.999 1.00 0.00
#> 3rd-C11_S58 1 0.000 0.999 1.00 0.00
#> 3rd-C12_S68 2 0.000 1.000 0.00 1.00
#> 3rd-C27_S49 2 0.000 1.000 0.00 1.00
#> 3rd-C33_S50 1 0.000 0.999 1.00 0.00
#> 3rd-C35_S23 2 0.000 1.000 0.00 1.00
#> 3rd-C36_S2 1 0.000 0.999 1.00 0.00
#> 3rd-C47_S35 2 0.000 1.000 0.00 1.00
#> 3rd-C49_S60 2 0.000 1.000 0.00 1.00
#> 3rd-C4_S25 1 0.000 0.999 1.00 0.00
#> 3rd-C53_S67 2 0.000 1.000 0.00 1.00
#> 3rd-C57_S5 2 0.000 1.000 0.00 1.00
#> 3rd-C58_S3 1 0.000 0.999 1.00 0.00
#> 3rd-C59_S91 1 0.000 0.999 1.00 0.00
#> 3rd-C65_S20 1 0.000 0.999 1.00 0.00
#> 3rd-C6_S44 2 0.141 0.980 0.02 0.98
#> 3rd-C71_S80 1 0.000 0.999 1.00 0.00
#> 3rd-C79_S67 2 0.000 1.000 0.00 1.00
#> 3rd-C82_S11 1 0.000 0.999 1.00 0.00
#> 3rd-C84_S75 1 0.000 0.999 1.00 0.00
#> 3rd-C85_S79 2 0.000 1.000 0.00 1.00
#> 3rd-C88_S24 1 0.000 0.999 1.00 0.00
#> 3rd-C91_S91 2 0.000 1.000 0.00 1.00
#> 3rd-C92_S86 1 0.000 0.999 1.00 0.00
#> 3rd-C95_S81 2 0.000 1.000 0.00 1.00
#> 3rd-C9_S5 2 0.000 1.000 0.00 1.00
#> 4th-61_S28 1 0.000 0.999 1.00 0.00
#> 4th-C14_S26 1 0.000 0.999 1.00 0.00
#> 4th-C18_S31 2 0.000 1.000 0.00 1.00
#> 4th-C24_S43 1 0.242 0.959 0.96 0.04
#> 4th-C26_S50 1 0.000 0.999 1.00 0.00
#> 4th-C36_S69 2 0.000 1.000 0.00 1.00
#> 4th-C40_S79 2 0.000 1.000 0.00 1.00
#> 4th-C4_S9 2 0.000 1.000 0.00 1.00
#> 4th-C56_S17 2 0.000 1.000 0.00 1.00
#> 4th-C5_S8 1 0.000 0.999 1.00 0.00
#> 4th-C62_S29 2 0.000 1.000 0.00 1.00
#> 4th-C64_S34 2 0.000 1.000 0.00 1.00
#> 4th-C66_S36 2 0.000 1.000 0.00 1.00
#> 4th-C67_S40 1 0.000 0.999 1.00 0.00
#> 4th-C73_S54 2 0.000 1.000 0.00 1.00
#> 4th-C75_S52 2 0.000 1.000 0.00 1.00
#> 4th-C79_S66 2 0.000 1.000 0.00 1.00
#> 4th-C7_S15 1 0.000 0.999 1.00 0.00
#> 4th-C80_S65 2 0.000 1.000 0.00 1.00
#> 4th-C82_S72 2 0.000 1.000 0.00 1.00
#> 4th-C83_S71 2 0.000 1.000 0.00 1.00
#> 4th-C85_S78 2 0.000 1.000 0.00 1.00
#> 4th-C86_S77 2 0.000 1.000 0.00 1.00
#> 4th-C88_S84 2 0.000 1.000 0.00 1.00
#> 4th-C89_S83 1 0.000 0.999 1.00 0.00
#> 4th-C92_S89 2 0.000 1.000 0.00 1.00
#> 4th-C94_S96 2 0.000 1.000 0.00 1.00
#> 4th-C96_S94 2 0.000 1.000 0.00 1.00
#> 5th-C34_S108 2 0.000 1.000 0.00 1.00
#> 5th-C35_S109 2 0.000 1.000 0.00 1.00
#> 5th-C49_S89 1 0.000 0.999 1.00 0.00
#> 5th-C5_S85 1 0.000 0.999 1.00 0.00
#> 5th-C7_S93 2 0.000 1.000 0.00 1.00
#> 5th-C90_S115 1 0.000 0.999 1.00 0.00
#> 5th-C9_S92 2 0.000 1.000 0.00 1.00
#> 6th-C12_S18 1 0.000 0.999 1.00 0.00
#> 6th-C20_S34 1 0.000 0.999 1.00 0.00
#> 6th-C21_S33 2 0.000 1.000 0.00 1.00
#> 6th-C22_S39 1 0.000 0.999 1.00 0.00
#> 6th-C23_S38 1 0.000 0.999 1.00 0.00
#> 6th-C24_S37 1 0.327 0.937 0.94 0.06
#> 6th-C29_S50 1 0.000 0.999 1.00 0.00
#> 6th-C2_S2 1 0.000 0.999 1.00 0.00
#> 6th-C30_S51 1 0.000 0.999 1.00 0.00
#> 6th-C40_S73 1 0.000 0.999 1.00 0.00
#> 6th-C42_S75 1 0.000 0.999 1.00 0.00
#> 6th-C51_S6 1 0.000 0.999 1.00 0.00
#> 6th-C54_S11 1 0.000 0.999 1.00 0.00
#> 6th-C59_S21 1 0.000 0.999 1.00 0.00
#> 6th-C63_S26 1 0.141 0.979 0.98 0.02
#> 6th-C66_S32 1 0.000 0.999 1.00 0.00
#> 6th-C71_S41 1 0.000 0.999 1.00 0.00
#> 6th-C73_S48 1 0.000 0.999 1.00 0.00
#> 6th-C75_S46 1 0.000 0.999 1.00 0.00
#> 6th-C77_S53 1 0.000 0.999 1.00 0.00
#> 6th-C79_S60 1 0.000 0.999 1.00 0.00
#> 6th-C80_S59 1 0.000 0.999 1.00 0.00
#> 6th-C85_S72 1 0.000 0.999 1.00 0.00
#> 6th-C87_S70 2 0.000 1.000 0.00 1.00
#> 7th-C10_S19 1 0.000 0.999 1.00 0.00
#> 7th-C11_S18 2 0.000 1.000 0.00 1.00
#> 7th-C14_S24 2 0.000 1.000 0.00 1.00
#> 7th-C24_S40 2 0.000 1.000 0.00 1.00
#> 7th-C25_S43 1 0.000 0.999 1.00 0.00
#> 7th-C31_S53 1 0.000 0.999 1.00 0.00
#> 7th-C36_S61 2 0.000 1.000 0.00 1.00
#> 7th-C45_S77 1 0.000 0.999 1.00 0.00
#> 7th-C50_S5 1 0.000 0.999 1.00 0.00
#> 7th-C53_S10 1 0.000 0.999 1.00 0.00
#> 7th-C58_S20 2 0.000 1.000 0.00 1.00
#> 7th-C59_S21 1 0.000 0.999 1.00 0.00
#> 7th-C62_S27 1 0.000 0.999 1.00 0.00
#> 7th-C64_S31 1 0.000 0.999 1.00 0.00
#> 7th-C66_S33 1 0.000 0.999 1.00 0.00
#> 7th-C73_S47 1 0.000 0.999 1.00 0.00
#> 7th-C77_S51 1 0.000 0.999 1.00 0.00
#> 7th-C79_S58 2 0.000 1.000 0.00 1.00
#> 7th-C80_S57 1 0.000 0.999 1.00 0.00
#> 7th-C82_S64 2 0.000 1.000 0.00 1.00
#> 7th-C84_S62 1 0.000 0.999 1.00 0.00
#> 7th-C89_S74 1 0.000 0.999 1.00 0.00
#> 7th-C8_S13 1 0.000 0.999 1.00 0.00
#> 7th-C90_S73 1 0.000 0.999 1.00 0.00
#> 7th-C96_S82 1 0.000 0.999 1.00 0.00
#> 8th-C10_S100 1 0.000 0.999 1.00 0.00
#> 8th-C24_S120 1 0.000 0.999 1.00 0.00
#> 8th-C2_S85 1 0.000 0.999 1.00 0.00
#> 8th-C44_S155 1 0.000 0.999 1.00 0.00
#> 8th-C55_S96 2 0.000 1.000 0.00 1.00
#> 8th-C57_S98 2 0.000 1.000 0.00 1.00
#> 8th-C58_S101 2 0.000 1.000 0.00 1.00
#> 8th-C65_S113 1 0.000 0.999 1.00 0.00
#> 8th-C67_S117 2 0.000 1.000 0.00 1.00
#> 8th-C74_S129 2 0.000 1.000 0.00 1.00
#> 8th-C85_S150 2 0.000 1.000 0.00 1.00
#> 8th-C87_S148 1 0.000 0.999 1.00 0.00
#> 9th-C10_S18 1 0.000 0.999 1.00 0.00
#> 9th-C11_S17 1 0.000 0.999 1.00 0.00
#> 9th-C1_S3 1 0.000 0.999 1.00 0.00
#> 9th-C38_S64 1 0.000 0.999 1.00 0.00
#> 9th-C3_S1 1 0.000 0.999 1.00 0.00
#> 9th-C41_S70 1 0.000 0.999 1.00 0.00
#> 9th-C46_S79 1 0.000 0.999 1.00 0.00
#> 9th-C57_S16 2 0.000 1.000 0.00 1.00
#> 9th-C6_S7 1 0.000 0.999 1.00 0.00
#> 9th-C70_S42 1 0.000 0.999 1.00 0.00
#> 9th-C80_S56 2 0.000 1.000 0.00 1.00
#> 9th-C81_S55 1 0.000 0.999 1.00 0.00
#> 9th-C83_S61 2 0.000 1.000 0.00 1.00
#> 9th-C86_S67 1 0.000 0.999 1.00 0.00
#> 9th-C89_S72 1 0.000 0.999 1.00 0.00
#> 9th-C8_S14 1 0.000 0.999 1.00 0.00
#> 9th-C93_S76 1 0.000 0.999 1.00 0.00
#> 9th-C9_S13 2 0.000 1.000 0.00 1.00
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> 10th_C13_S61 1 0.0000 0.9658 1.00 0.00 0.00
#> 10th_C19_S62 3 0.0000 0.9814 0.00 0.00 1.00
#> 10th_C81_S70 3 0.0000 0.9814 0.00 0.00 1.00
#> 10th_C84_S115 3 0.0000 0.9814 0.00 0.00 1.00
#> 11th-C41_S60 3 0.0000 0.9814 0.00 0.00 1.00
#> 11th-C44_S15 3 0.0000 0.9814 0.00 0.00 1.00
#> 11th-C49_S23 3 0.0000 0.9814 0.00 0.00 1.00
#> 11th-C51_S39 3 0.0000 0.9814 0.00 0.00 1.00
#> 11th-C53_S78 3 0.0000 0.9814 0.00 0.00 1.00
#> 11th-C66_S88 1 0.0000 0.9658 1.00 0.00 0.00
#> 11th-C7_S16 3 0.3340 0.8575 0.00 0.12 0.88
#> 12th-C14_S190 3 0.0000 0.9814 0.00 0.00 1.00
#> 12th-C24_S141 3 0.0000 0.9814 0.00 0.00 1.00
#> 12th-C29_S150 2 0.0000 0.9921 0.00 1.00 0.00
#> 12th-C42_S159 3 0.0000 0.9814 0.00 0.00 1.00
#> 12th-C55_S203 3 0.0000 0.9814 0.00 0.00 1.00
#> 12th-C58_S162 2 0.0000 0.9921 0.00 1.00 0.00
#> 12th-C59_S169 1 0.0000 0.9658 1.00 0.00 0.00
#> 12th-C60_S176 1 0.4002 0.8021 0.84 0.00 0.16
#> 12th-C64_S163 1 0.0000 0.9658 1.00 0.00 0.00
#> 12th-C65_S170 3 0.0000 0.9814 0.00 0.00 1.00
#> 12th-C74_S214 1 0.0000 0.9658 1.00 0.00 0.00
#> 12th-C76_S177 1 0.0000 0.9658 1.00 0.00 0.00
#> 12th-C7_S196 3 0.0000 0.9814 0.00 0.00 1.00
#> 12th-C84_S165 1 0.0000 0.9658 1.00 0.00 0.00
#> 12th-C90_S166 3 0.0000 0.9814 0.00 0.00 1.00
#> 12th-C95_S174 2 0.0000 0.9921 0.00 1.00 0.00
#> 12th-C96_S167 1 0.0000 0.9658 1.00 0.00 0.00
#> 13th_C34_S181 3 0.0000 0.9814 0.00 0.00 1.00
#> 13th_C66_S214 2 0.0000 0.9921 0.00 1.00 0.00
#> 13th_C76_S216 2 0.0000 0.9921 0.00 1.00 0.00
#> 1st-61_S27 1 0.0000 0.9658 1.00 0.00 0.00
#> 1st-C11_S58 1 0.0000 0.9658 1.00 0.00 0.00
#> 1st-C19_S20 2 0.0000 0.9921 0.00 1.00 0.00
#> 1st-C32_S14 3 0.0000 0.9814 0.00 0.00 1.00
#> 1st-C42_S71 3 0.5216 0.6511 0.00 0.26 0.74
#> 1st-C50_S33 2 0.0000 0.9921 0.00 1.00 0.00
#> 1st-C56_S34 2 0.0000 0.9921 0.00 1.00 0.00
#> 1st-C57_S42 2 0.0000 0.9921 0.00 1.00 0.00
#> 1st-C58_S76 1 0.0000 0.9658 1.00 0.00 0.00
#> 1st-C64_S79 1 0.0000 0.9658 1.00 0.00 0.00
#> 1st-C68_S36 2 0.0000 0.9921 0.00 1.00 0.00
#> 1st-C73_S45 2 0.0000 0.9921 0.00 1.00 0.00
#> 1st-C75_S29 2 0.0000 0.9921 0.00 1.00 0.00
#> 1st-C77_S86 3 0.1529 0.9450 0.00 0.04 0.96
#> 1st-C78_S85 2 0.0000 0.9921 0.00 1.00 0.00
#> 1st-C80_S38 2 0.0000 0.9921 0.00 1.00 0.00
#> 1st-C90_S91 1 0.0000 0.9658 1.00 0.00 0.00
#> 2nd-C11_S20 2 0.0000 0.9921 0.00 1.00 0.00
#> 2nd-C15_S25 1 0.0000 0.9658 1.00 0.00 0.00
#> 2nd-C16_S33 2 0.0000 0.9921 0.00 1.00 0.00
#> 2nd-C17_S32 1 0.0000 0.9658 1.00 0.00 0.00
#> 2nd-C21_S37 3 0.0000 0.9814 0.00 0.00 1.00
#> 2nd-C26_S50 2 0.0000 0.9921 0.00 1.00 0.00
#> 2nd-C32_S62 1 0.0000 0.9658 1.00 0.00 0.00
#> 2nd-C38_S74 1 0.0000 0.9658 1.00 0.00 0.00
#> 2nd-C39_S75 2 0.0000 0.9921 0.00 1.00 0.00
#> 2nd-C62_S29 1 0.0000 0.9658 1.00 0.00 0.00
#> 2nd-C67_S40 2 0.0000 0.9921 0.00 1.00 0.00
#> 2nd-C72_S48 1 0.5397 0.6201 0.72 0.00 0.28
#> 2nd-C75_S52 2 0.0000 0.9921 0.00 1.00 0.00
#> 2nd-C77_S59 2 0.0000 0.9921 0.00 1.00 0.00
#> 2nd-C80_S65 2 0.0000 0.9921 0.00 1.00 0.00
#> 2nd-C86_S77 3 0.0000 0.9814 0.00 0.00 1.00
#> 2nd-C88_S84 1 0.6309 0.0335 0.50 0.00 0.50
#> 2nd-C8_S14 2 0.0000 0.9921 0.00 1.00 0.00
#> 2nd-C93_S88 1 0.0892 0.9489 0.98 0.00 0.02
#> 2nd-C95_S95 3 0.0000 0.9814 0.00 0.00 1.00
#> 3rd-C11_S58 1 0.0000 0.9658 1.00 0.00 0.00
#> 3rd-C12_S68 2 0.0000 0.9921 0.00 1.00 0.00
#> 3rd-C27_S49 2 0.0000 0.9921 0.00 1.00 0.00
#> 3rd-C33_S50 1 0.0000 0.9658 1.00 0.00 0.00
#> 3rd-C35_S23 3 0.0000 0.9814 0.00 0.00 1.00
#> 3rd-C36_S2 1 0.0000 0.9658 1.00 0.00 0.00
#> 3rd-C47_S35 2 0.0000 0.9921 0.00 1.00 0.00
#> 3rd-C49_S60 2 0.0000 0.9921 0.00 1.00 0.00
#> 3rd-C4_S25 1 0.0000 0.9658 1.00 0.00 0.00
#> 3rd-C53_S67 1 0.6045 0.3862 0.62 0.38 0.00
#> 3rd-C57_S5 2 0.0000 0.9921 0.00 1.00 0.00
#> 3rd-C58_S3 1 0.0000 0.9658 1.00 0.00 0.00
#> 3rd-C59_S91 1 0.0000 0.9658 1.00 0.00 0.00
#> 3rd-C65_S20 3 0.0000 0.9814 0.00 0.00 1.00
#> 3rd-C6_S44 3 0.0000 0.9814 0.00 0.00 1.00
#> 3rd-C71_S80 1 0.0000 0.9658 1.00 0.00 0.00
#> 3rd-C79_S67 2 0.0000 0.9921 0.00 1.00 0.00
#> 3rd-C82_S11 1 0.0000 0.9658 1.00 0.00 0.00
#> 3rd-C84_S75 1 0.0000 0.9658 1.00 0.00 0.00
#> 3rd-C85_S79 2 0.0000 0.9921 0.00 1.00 0.00
#> 3rd-C88_S24 1 0.0000 0.9658 1.00 0.00 0.00
#> 3rd-C91_S91 2 0.0000 0.9921 0.00 1.00 0.00
#> 3rd-C92_S86 1 0.4555 0.7500 0.80 0.00 0.20
#> 3rd-C95_S81 2 0.0000 0.9921 0.00 1.00 0.00
#> 3rd-C9_S5 3 0.0892 0.9637 0.00 0.02 0.98
#> 4th-61_S28 1 0.0000 0.9658 1.00 0.00 0.00
#> 4th-C14_S26 1 0.0000 0.9658 1.00 0.00 0.00
#> 4th-C18_S31 2 0.0000 0.9921 0.00 1.00 0.00
#> 4th-C24_S43 1 0.0000 0.9658 1.00 0.00 0.00
#> 4th-C26_S50 1 0.0000 0.9658 1.00 0.00 0.00
#> 4th-C36_S69 3 0.5560 0.5749 0.00 0.30 0.70
#> 4th-C40_S79 2 0.0000 0.9921 0.00 1.00 0.00
#> 4th-C4_S9 2 0.0000 0.9921 0.00 1.00 0.00
#> 4th-C56_S17 2 0.3340 0.8620 0.00 0.88 0.12
#> 4th-C5_S8 1 0.0000 0.9658 1.00 0.00 0.00
#> 4th-C62_S29 2 0.0000 0.9921 0.00 1.00 0.00
#> 4th-C64_S34 2 0.0000 0.9921 0.00 1.00 0.00
#> 4th-C66_S36 2 0.0000 0.9921 0.00 1.00 0.00
#> 4th-C67_S40 3 0.0000 0.9814 0.00 0.00 1.00
#> 4th-C73_S54 2 0.0000 0.9921 0.00 1.00 0.00
#> 4th-C75_S52 2 0.0000 0.9921 0.00 1.00 0.00
#> 4th-C79_S66 2 0.0000 0.9921 0.00 1.00 0.00
#> 4th-C7_S15 1 0.0000 0.9658 1.00 0.00 0.00
#> 4th-C80_S65 2 0.0000 0.9921 0.00 1.00 0.00
#> 4th-C82_S72 2 0.0000 0.9921 0.00 1.00 0.00
#> 4th-C83_S71 2 0.0000 0.9921 0.00 1.00 0.00
#> 4th-C85_S78 1 0.0000 0.9658 1.00 0.00 0.00
#> 4th-C86_S77 2 0.0000 0.9921 0.00 1.00 0.00
#> 4th-C88_S84 2 0.0000 0.9921 0.00 1.00 0.00
#> 4th-C89_S83 1 0.0000 0.9658 1.00 0.00 0.00
#> 4th-C92_S89 2 0.0000 0.9921 0.00 1.00 0.00
#> 4th-C94_S96 2 0.4002 0.8092 0.00 0.84 0.16
#> 4th-C96_S94 2 0.0000 0.9921 0.00 1.00 0.00
#> 5th-C34_S108 2 0.0000 0.9921 0.00 1.00 0.00
#> 5th-C35_S109 3 0.0000 0.9814 0.00 0.00 1.00
#> 5th-C49_S89 1 0.0000 0.9658 1.00 0.00 0.00
#> 5th-C5_S85 1 0.0000 0.9658 1.00 0.00 0.00
#> 5th-C7_S93 1 0.0000 0.9658 1.00 0.00 0.00
#> 5th-C90_S115 3 0.0000 0.9814 0.00 0.00 1.00
#> 5th-C9_S92 2 0.0000 0.9921 0.00 1.00 0.00
#> 6th-C12_S18 1 0.0000 0.9658 1.00 0.00 0.00
#> 6th-C20_S34 3 0.0000 0.9814 0.00 0.00 1.00
#> 6th-C21_S33 2 0.0000 0.9921 0.00 1.00 0.00
#> 6th-C22_S39 3 0.0000 0.9814 0.00 0.00 1.00
#> 6th-C23_S38 1 0.0000 0.9658 1.00 0.00 0.00
#> 6th-C24_S37 3 0.0000 0.9814 0.00 0.00 1.00
#> 6th-C29_S50 1 0.0000 0.9658 1.00 0.00 0.00
#> 6th-C2_S2 3 0.0000 0.9814 0.00 0.00 1.00
#> 6th-C30_S51 3 0.0000 0.9814 0.00 0.00 1.00
#> 6th-C40_S73 3 0.0000 0.9814 0.00 0.00 1.00
#> 6th-C42_S75 3 0.0000 0.9814 0.00 0.00 1.00
#> 6th-C51_S6 3 0.0000 0.9814 0.00 0.00 1.00
#> 6th-C54_S11 1 0.0000 0.9658 1.00 0.00 0.00
#> 6th-C59_S21 1 0.0000 0.9658 1.00 0.00 0.00
#> 6th-C63_S26 1 0.0000 0.9658 1.00 0.00 0.00
#> 6th-C66_S32 3 0.0000 0.9814 0.00 0.00 1.00
#> 6th-C71_S41 1 0.0000 0.9658 1.00 0.00 0.00
#> 6th-C73_S48 3 0.0000 0.9814 0.00 0.00 1.00
#> 6th-C75_S46 3 0.0000 0.9814 0.00 0.00 1.00
#> 6th-C77_S53 1 0.0000 0.9658 1.00 0.00 0.00
#> 6th-C79_S60 1 0.6192 0.3043 0.58 0.00 0.42
#> 6th-C80_S59 3 0.0000 0.9814 0.00 0.00 1.00
#> 6th-C85_S72 1 0.0000 0.9658 1.00 0.00 0.00
#> 6th-C87_S70 2 0.0000 0.9921 0.00 1.00 0.00
#> 7th-C10_S19 3 0.0000 0.9814 0.00 0.00 1.00
#> 7th-C11_S18 2 0.0000 0.9921 0.00 1.00 0.00
#> 7th-C14_S24 2 0.0000 0.9921 0.00 1.00 0.00
#> 7th-C24_S40 2 0.0000 0.9921 0.00 1.00 0.00
#> 7th-C25_S43 1 0.0000 0.9658 1.00 0.00 0.00
#> 7th-C31_S53 3 0.0000 0.9814 0.00 0.00 1.00
#> 7th-C36_S61 2 0.0000 0.9921 0.00 1.00 0.00
#> 7th-C45_S77 1 0.0000 0.9658 1.00 0.00 0.00
#> 7th-C50_S5 3 0.2537 0.8986 0.08 0.00 0.92
#> 7th-C53_S10 1 0.0000 0.9658 1.00 0.00 0.00
#> 7th-C58_S20 2 0.0000 0.9921 0.00 1.00 0.00
#> 7th-C59_S21 1 0.0000 0.9658 1.00 0.00 0.00
#> 7th-C62_S27 1 0.0000 0.9658 1.00 0.00 0.00
#> 7th-C64_S31 1 0.0000 0.9658 1.00 0.00 0.00
#> 7th-C66_S33 3 0.0000 0.9814 0.00 0.00 1.00
#> 7th-C73_S47 3 0.0000 0.9814 0.00 0.00 1.00
#> 7th-C77_S51 1 0.0000 0.9658 1.00 0.00 0.00
#> 7th-C79_S58 2 0.0000 0.9921 0.00 1.00 0.00
#> 7th-C80_S57 3 0.0000 0.9814 0.00 0.00 1.00
#> 7th-C82_S64 2 0.0000 0.9921 0.00 1.00 0.00
#> 7th-C84_S62 1 0.0000 0.9658 1.00 0.00 0.00
#> 7th-C89_S74 3 0.0000 0.9814 0.00 0.00 1.00
#> 7th-C8_S13 1 0.0000 0.9658 1.00 0.00 0.00
#> 7th-C90_S73 1 0.0000 0.9658 1.00 0.00 0.00
#> 7th-C96_S82 1 0.0000 0.9658 1.00 0.00 0.00
#> 8th-C10_S100 1 0.0000 0.9658 1.00 0.00 0.00
#> 8th-C24_S120 1 0.6045 0.4162 0.62 0.00 0.38
#> 8th-C2_S85 1 0.0000 0.9658 1.00 0.00 0.00
#> 8th-C44_S155 3 0.0000 0.9814 0.00 0.00 1.00
#> 8th-C55_S96 2 0.0000 0.9921 0.00 1.00 0.00
#> 8th-C57_S98 2 0.0000 0.9921 0.00 1.00 0.00
#> 8th-C58_S101 2 0.0000 0.9921 0.00 1.00 0.00
#> 8th-C65_S113 1 0.0000 0.9658 1.00 0.00 0.00
#> 8th-C67_S117 2 0.0000 0.9921 0.00 1.00 0.00
#> 8th-C74_S129 2 0.0000 0.9921 0.00 1.00 0.00
#> 8th-C85_S150 2 0.0000 0.9921 0.00 1.00 0.00
#> 8th-C87_S148 1 0.2537 0.8934 0.92 0.00 0.08
#> 9th-C10_S18 3 0.0000 0.9814 0.00 0.00 1.00
#> 9th-C11_S17 3 0.0000 0.9814 0.00 0.00 1.00
#> 9th-C1_S3 3 0.0000 0.9814 0.00 0.00 1.00
#> 9th-C38_S64 3 0.0000 0.9814 0.00 0.00 1.00
#> 9th-C3_S1 3 0.0000 0.9814 0.00 0.00 1.00
#> 9th-C41_S70 1 0.0000 0.9658 1.00 0.00 0.00
#> 9th-C46_S79 3 0.0000 0.9814 0.00 0.00 1.00
#> 9th-C57_S16 2 0.5216 0.6464 0.00 0.74 0.26
#> 9th-C6_S7 3 0.0000 0.9814 0.00 0.00 1.00
#> 9th-C70_S42 1 0.0000 0.9658 1.00 0.00 0.00
#> 9th-C80_S56 2 0.0000 0.9921 0.00 1.00 0.00
#> 9th-C81_S55 3 0.0000 0.9814 0.00 0.00 1.00
#> 9th-C83_S61 2 0.0000 0.9921 0.00 1.00 0.00
#> 9th-C86_S67 3 0.5397 0.5948 0.28 0.00 0.72
#> 9th-C89_S72 3 0.0000 0.9814 0.00 0.00 1.00
#> 9th-C8_S14 3 0.0000 0.9814 0.00 0.00 1.00
#> 9th-C93_S76 3 0.0000 0.9814 0.00 0.00 1.00
#> 9th-C9_S13 2 0.0000 0.9921 0.00 1.00 0.00
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> 10th_C13_S61 1 0.3606 0.81238 0.84 0.00 0.14 0.02
#> 10th_C19_S62 2 0.3610 0.71904 0.00 0.80 0.20 0.00
#> 10th_C81_S70 3 0.0000 0.95924 0.00 0.00 1.00 0.00
#> 10th_C84_S115 3 0.0707 0.95556 0.00 0.00 0.98 0.02
#> 11th-C41_S60 3 0.0707 0.95556 0.00 0.00 0.98 0.02
#> 11th-C44_S15 3 0.0000 0.95924 0.00 0.00 1.00 0.00
#> 11th-C49_S23 3 0.0000 0.95924 0.00 0.00 1.00 0.00
#> 11th-C51_S39 3 0.0000 0.95924 0.00 0.00 1.00 0.00
#> 11th-C53_S78 3 0.0707 0.95556 0.00 0.00 0.98 0.02
#> 11th-C66_S88 1 0.0707 0.94926 0.98 0.00 0.00 0.02
#> 11th-C7_S16 2 0.1637 0.88750 0.00 0.94 0.06 0.00
#> 12th-C14_S190 3 0.0707 0.95556 0.00 0.00 0.98 0.02
#> 12th-C24_S141 3 0.0707 0.95556 0.00 0.00 0.98 0.02
#> 12th-C29_S150 2 0.0707 0.94197 0.00 0.98 0.00 0.02
#> 12th-C42_S159 3 0.0000 0.95924 0.00 0.00 1.00 0.00
#> 12th-C55_S203 3 0.0000 0.95924 0.00 0.00 1.00 0.00
#> 12th-C58_S162 4 0.2345 0.88717 0.00 0.10 0.00 0.90
#> 12th-C59_S169 1 0.0707 0.94904 0.98 0.00 0.00 0.02
#> 12th-C60_S176 1 0.5570 0.17317 0.54 0.00 0.44 0.02
#> 12th-C64_S163 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 12th-C65_S170 3 0.0000 0.95924 0.00 0.00 1.00 0.00
#> 12th-C74_S214 1 0.1211 0.94101 0.96 0.00 0.00 0.04
#> 12th-C76_S177 1 0.0707 0.94912 0.98 0.02 0.00 0.00
#> 12th-C7_S196 3 0.0707 0.95556 0.00 0.00 0.98 0.02
#> 12th-C84_S165 1 0.1211 0.94101 0.96 0.00 0.00 0.04
#> 12th-C90_S166 3 0.0707 0.95556 0.00 0.00 0.98 0.02
#> 12th-C95_S174 4 0.0707 0.92359 0.00 0.02 0.00 0.98
#> 12th-C96_S167 1 0.0707 0.94926 0.98 0.00 0.00 0.02
#> 13th_C34_S181 3 0.0000 0.95924 0.00 0.00 1.00 0.00
#> 13th_C66_S214 2 0.5000 -0.16329 0.00 0.50 0.00 0.50
#> 13th_C76_S216 2 0.0707 0.94197 0.00 0.98 0.00 0.02
#> 1st-61_S27 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 1st-C11_S58 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 1st-C19_S20 2 0.0707 0.94197 0.00 0.98 0.00 0.02
#> 1st-C32_S14 3 0.0000 0.95924 0.00 0.00 1.00 0.00
#> 1st-C42_S71 2 0.1913 0.90245 0.00 0.94 0.02 0.04
#> 1st-C50_S33 2 0.0707 0.94197 0.00 0.98 0.00 0.02
#> 1st-C56_S34 4 0.0707 0.92359 0.00 0.02 0.00 0.98
#> 1st-C57_S42 2 0.0707 0.94197 0.00 0.98 0.00 0.02
#> 1st-C58_S76 1 0.1211 0.93052 0.96 0.00 0.04 0.00
#> 1st-C64_S79 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 1st-C68_S36 4 0.4624 0.58720 0.00 0.34 0.00 0.66
#> 1st-C73_S45 2 0.0707 0.94197 0.00 0.98 0.00 0.02
#> 1st-C75_S29 4 0.2647 0.87319 0.00 0.12 0.00 0.88
#> 1st-C77_S86 2 0.0707 0.91979 0.00 0.98 0.02 0.00
#> 1st-C78_S85 2 0.0707 0.94197 0.00 0.98 0.00 0.02
#> 1st-C80_S38 4 0.2345 0.88717 0.00 0.10 0.00 0.90
#> 1st-C90_S91 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 2nd-C11_S20 4 0.1211 0.91762 0.00 0.04 0.00 0.96
#> 2nd-C15_S25 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 2nd-C16_S33 4 0.0707 0.92359 0.00 0.02 0.00 0.98
#> 2nd-C17_S32 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 2nd-C21_S37 3 0.0707 0.94754 0.00 0.02 0.98 0.00
#> 2nd-C26_S50 4 0.3801 0.77933 0.00 0.22 0.00 0.78
#> 2nd-C32_S62 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 2nd-C38_S74 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 2nd-C39_S75 4 0.0707 0.92359 0.00 0.02 0.00 0.98
#> 2nd-C62_S29 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 2nd-C67_S40 2 0.3172 0.79691 0.00 0.84 0.00 0.16
#> 2nd-C72_S48 3 0.5271 0.47687 0.34 0.00 0.64 0.02
#> 2nd-C75_S52 4 0.0707 0.92359 0.00 0.02 0.00 0.98
#> 2nd-C77_S59 2 0.0707 0.94197 0.00 0.98 0.00 0.02
#> 2nd-C80_S65 4 0.0707 0.92359 0.00 0.02 0.00 0.98
#> 2nd-C86_S77 3 0.0000 0.95924 0.00 0.00 1.00 0.00
#> 2nd-C88_S84 3 0.4624 0.50262 0.34 0.00 0.66 0.00
#> 2nd-C8_S14 2 0.0707 0.94197 0.00 0.98 0.00 0.02
#> 2nd-C93_S88 1 0.2921 0.82525 0.86 0.00 0.14 0.00
#> 2nd-C95_S95 3 0.0000 0.95924 0.00 0.00 1.00 0.00
#> 3rd-C11_S58 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 3rd-C12_S68 2 0.0707 0.94197 0.00 0.98 0.00 0.02
#> 3rd-C27_S49 2 0.0707 0.94197 0.00 0.98 0.00 0.02
#> 3rd-C33_S50 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 3rd-C35_S23 2 0.4406 0.57124 0.00 0.70 0.30 0.00
#> 3rd-C36_S2 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 3rd-C47_S35 2 0.0707 0.94197 0.00 0.98 0.00 0.02
#> 3rd-C49_S60 2 0.0707 0.94197 0.00 0.98 0.00 0.02
#> 3rd-C4_S25 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 3rd-C53_S67 4 0.1211 0.88433 0.04 0.00 0.00 0.96
#> 3rd-C57_S5 4 0.4134 0.72440 0.00 0.26 0.00 0.74
#> 3rd-C58_S3 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 3rd-C59_S91 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 3rd-C65_S20 3 0.0000 0.95924 0.00 0.00 1.00 0.00
#> 3rd-C6_S44 3 0.1211 0.93169 0.00 0.04 0.96 0.00
#> 3rd-C71_S80 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 3rd-C79_S67 4 0.3801 0.77813 0.00 0.22 0.00 0.78
#> 3rd-C82_S11 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 3rd-C84_S75 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 3rd-C85_S79 4 0.1637 0.90870 0.00 0.06 0.00 0.94
#> 3rd-C88_S24 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 3rd-C91_S91 4 0.1211 0.91762 0.00 0.04 0.00 0.96
#> 3rd-C92_S86 3 0.5000 0.00753 0.50 0.00 0.50 0.00
#> 3rd-C95_S81 4 0.3610 0.80027 0.00 0.20 0.00 0.80
#> 3rd-C9_S5 2 0.0707 0.91979 0.00 0.98 0.02 0.00
#> 4th-61_S28 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 4th-C14_S26 1 0.1637 0.91154 0.94 0.00 0.06 0.00
#> 4th-C18_S31 2 0.0707 0.94197 0.00 0.98 0.00 0.02
#> 4th-C24_S43 1 0.2345 0.88088 0.90 0.00 0.00 0.10
#> 4th-C26_S50 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 4th-C36_S69 2 0.0707 0.91979 0.00 0.98 0.02 0.00
#> 4th-C40_S79 4 0.0707 0.92359 0.00 0.02 0.00 0.98
#> 4th-C4_S9 2 0.0707 0.94197 0.00 0.98 0.00 0.02
#> 4th-C56_S17 2 0.0707 0.91979 0.00 0.98 0.02 0.00
#> 4th-C5_S8 1 0.1211 0.93596 0.96 0.00 0.00 0.04
#> 4th-C62_S29 4 0.0707 0.92359 0.00 0.02 0.00 0.98
#> 4th-C64_S34 4 0.0707 0.92359 0.00 0.02 0.00 0.98
#> 4th-C66_S36 4 0.0707 0.92359 0.00 0.02 0.00 0.98
#> 4th-C67_S40 3 0.0000 0.95924 0.00 0.00 1.00 0.00
#> 4th-C73_S54 2 0.0707 0.94197 0.00 0.98 0.00 0.02
#> 4th-C75_S52 2 0.0707 0.94197 0.00 0.98 0.00 0.02
#> 4th-C79_S66 2 0.0707 0.94197 0.00 0.98 0.00 0.02
#> 4th-C7_S15 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 4th-C80_S65 4 0.0707 0.92359 0.00 0.02 0.00 0.98
#> 4th-C82_S72 4 0.0707 0.92359 0.00 0.02 0.00 0.98
#> 4th-C83_S71 2 0.0707 0.94197 0.00 0.98 0.00 0.02
#> 4th-C85_S78 4 0.2011 0.84794 0.08 0.00 0.00 0.92
#> 4th-C86_S77 4 0.0707 0.92359 0.00 0.02 0.00 0.98
#> 4th-C88_S84 4 0.0707 0.92359 0.00 0.02 0.00 0.98
#> 4th-C89_S83 1 0.1637 0.91992 0.94 0.00 0.00 0.06
#> 4th-C92_S89 4 0.0707 0.92359 0.00 0.02 0.00 0.98
#> 4th-C94_S96 2 0.0707 0.91979 0.00 0.98 0.02 0.00
#> 4th-C96_S94 2 0.2011 0.89153 0.00 0.92 0.00 0.08
#> 5th-C34_S108 4 0.0707 0.92359 0.00 0.02 0.00 0.98
#> 5th-C35_S109 2 0.2647 0.82182 0.00 0.88 0.12 0.00
#> 5th-C49_S89 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 5th-C5_S85 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 5th-C7_S93 1 0.4977 0.19575 0.54 0.00 0.00 0.46
#> 5th-C90_S115 3 0.0000 0.95924 0.00 0.00 1.00 0.00
#> 5th-C9_S92 4 0.0707 0.92359 0.00 0.02 0.00 0.98
#> 6th-C12_S18 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 6th-C20_S34 3 0.0707 0.95556 0.00 0.00 0.98 0.02
#> 6th-C21_S33 2 0.0707 0.94197 0.00 0.98 0.00 0.02
#> 6th-C22_S39 3 0.0000 0.95924 0.00 0.00 1.00 0.00
#> 6th-C23_S38 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 6th-C24_S37 3 0.1211 0.93265 0.00 0.04 0.96 0.00
#> 6th-C29_S50 1 0.0707 0.94926 0.98 0.00 0.00 0.02
#> 6th-C2_S2 3 0.0000 0.95924 0.00 0.00 1.00 0.00
#> 6th-C30_S51 3 0.0000 0.95924 0.00 0.00 1.00 0.00
#> 6th-C40_S73 3 0.0707 0.95556 0.00 0.00 0.98 0.02
#> 6th-C42_S75 3 0.0707 0.95556 0.00 0.00 0.98 0.02
#> 6th-C51_S6 3 0.0000 0.95924 0.00 0.00 1.00 0.00
#> 6th-C54_S11 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 6th-C59_S21 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 6th-C63_S26 1 0.1637 0.91874 0.94 0.00 0.00 0.06
#> 6th-C66_S32 3 0.0707 0.95556 0.00 0.00 0.98 0.02
#> 6th-C71_S41 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 6th-C73_S48 3 0.0000 0.95924 0.00 0.00 1.00 0.00
#> 6th-C75_S46 3 0.0000 0.95924 0.00 0.00 1.00 0.00
#> 6th-C77_S53 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 6th-C79_S60 3 0.4642 0.67533 0.24 0.00 0.74 0.02
#> 6th-C80_S59 3 0.0707 0.95556 0.00 0.00 0.98 0.02
#> 6th-C85_S72 1 0.0707 0.94904 0.98 0.00 0.00 0.02
#> 6th-C87_S70 2 0.3400 0.76642 0.00 0.82 0.00 0.18
#> 7th-C10_S19 3 0.0000 0.95924 0.00 0.00 1.00 0.00
#> 7th-C11_S18 2 0.0707 0.94197 0.00 0.98 0.00 0.02
#> 7th-C14_S24 4 0.1211 0.91762 0.00 0.04 0.00 0.96
#> 7th-C24_S40 4 0.0707 0.92359 0.00 0.02 0.00 0.98
#> 7th-C25_S43 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 7th-C31_S53 3 0.0000 0.95924 0.00 0.00 1.00 0.00
#> 7th-C36_S61 2 0.0707 0.94197 0.00 0.98 0.00 0.02
#> 7th-C45_S77 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 7th-C50_S5 3 0.1411 0.94230 0.02 0.00 0.96 0.02
#> 7th-C53_S10 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 7th-C58_S20 4 0.0707 0.92359 0.00 0.02 0.00 0.98
#> 7th-C59_S21 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 7th-C62_S27 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 7th-C64_S31 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 7th-C66_S33 3 0.0707 0.95556 0.00 0.00 0.98 0.02
#> 7th-C73_S47 3 0.0000 0.95924 0.00 0.00 1.00 0.00
#> 7th-C77_S51 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 7th-C79_S58 2 0.0707 0.94197 0.00 0.98 0.00 0.02
#> 7th-C80_S57 3 0.0000 0.95924 0.00 0.00 1.00 0.00
#> 7th-C82_S64 4 0.3400 0.82428 0.00 0.18 0.00 0.82
#> 7th-C84_S62 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 7th-C89_S74 3 0.0000 0.95924 0.00 0.00 1.00 0.00
#> 7th-C8_S13 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 7th-C90_S73 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 7th-C96_S82 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 8th-C10_S100 1 0.0000 0.95961 1.00 0.00 0.00 0.00
#> 8th-C24_S120 3 0.3606 0.81691 0.14 0.00 0.84 0.02
#> 8th-C2_S85 1 0.0707 0.94904 0.98 0.00 0.00 0.02
#> 8th-C44_S155 3 0.0000 0.95924 0.00 0.00 1.00 0.00
#> 8th-C55_S96 2 0.0707 0.94197 0.00 0.98 0.00 0.02
#> 8th-C57_S98 2 0.0707 0.94197 0.00 0.98 0.00 0.02
#> 8th-C58_S101 4 0.4406 0.66068 0.00 0.30 0.00 0.70
#> 8th-C65_S113 1 0.3198 0.86905 0.88 0.00 0.08 0.04
#> 8th-C67_S117 2 0.1913 0.90245 0.00 0.94 0.02 0.04
#> 8th-C74_S129 2 0.3172 0.79671 0.00 0.84 0.00 0.16
#> 8th-C85_S150 2 0.1211 0.92732 0.00 0.96 0.00 0.04
#> 8th-C87_S148 1 0.5594 0.07503 0.52 0.00 0.46 0.02
#> 9th-C10_S18 3 0.0707 0.95556 0.00 0.00 0.98 0.02
#> 9th-C11_S17 3 0.0707 0.95556 0.00 0.00 0.98 0.02
#> 9th-C1_S3 3 0.0000 0.95924 0.00 0.00 1.00 0.00
#> 9th-C38_S64 3 0.0707 0.95556 0.00 0.00 0.98 0.02
#> 9th-C3_S1 3 0.0000 0.95924 0.00 0.00 1.00 0.00
#> 9th-C41_S70 1 0.2335 0.89852 0.92 0.00 0.06 0.02
#> 9th-C46_S79 3 0.0707 0.95556 0.00 0.00 0.98 0.02
#> 9th-C57_S16 2 0.0707 0.91979 0.00 0.98 0.02 0.00
#> 9th-C6_S7 3 0.0000 0.95924 0.00 0.00 1.00 0.00
#> 9th-C70_S42 1 0.0707 0.94926 0.98 0.00 0.00 0.02
#> 9th-C80_S56 2 0.0707 0.94197 0.00 0.98 0.00 0.02
#> 9th-C81_S55 3 0.0000 0.95924 0.00 0.00 1.00 0.00
#> 9th-C83_S61 4 0.4855 0.44275 0.00 0.40 0.00 0.60
#> 9th-C86_S67 3 0.2706 0.88298 0.08 0.00 0.90 0.02
#> 9th-C89_S72 3 0.0707 0.95556 0.00 0.00 0.98 0.02
#> 9th-C8_S14 3 0.0707 0.95556 0.00 0.00 0.98 0.02
#> 9th-C93_S76 3 0.0000 0.95924 0.00 0.00 1.00 0.00
#> 9th-C9_S13 2 0.0707 0.94197 0.00 0.98 0.00 0.02
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
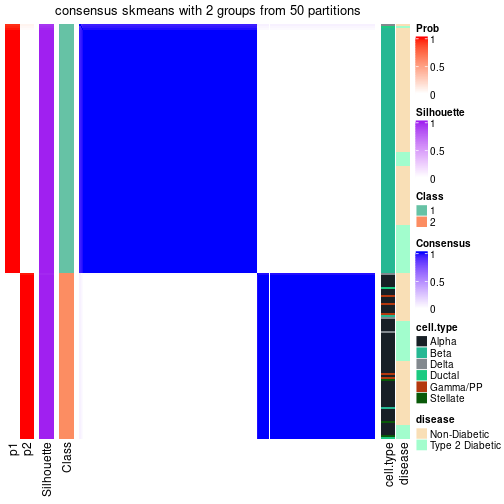
consensus_heatmap(res, k = 3)
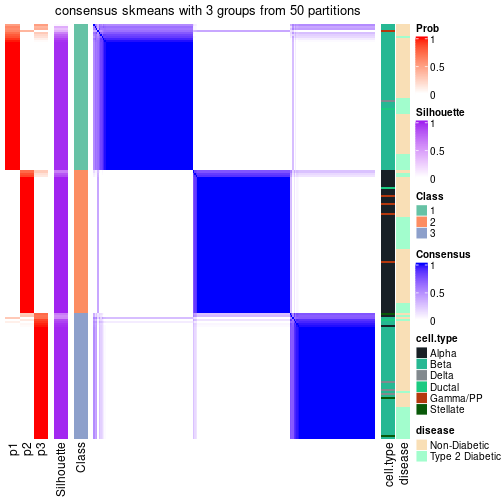
consensus_heatmap(res, k = 4)
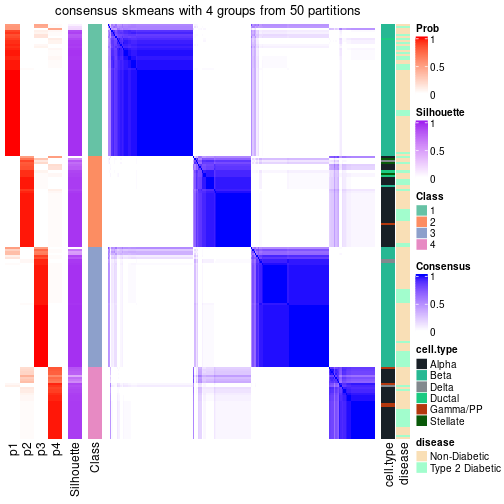
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
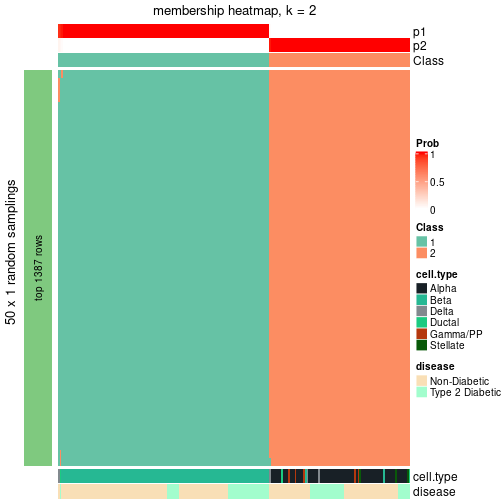
membership_heatmap(res, k = 3)
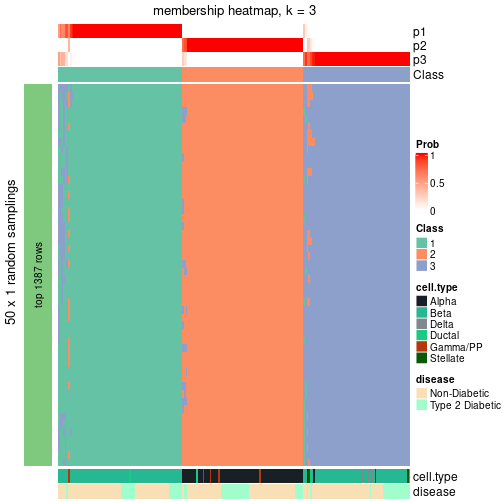
membership_heatmap(res, k = 4)
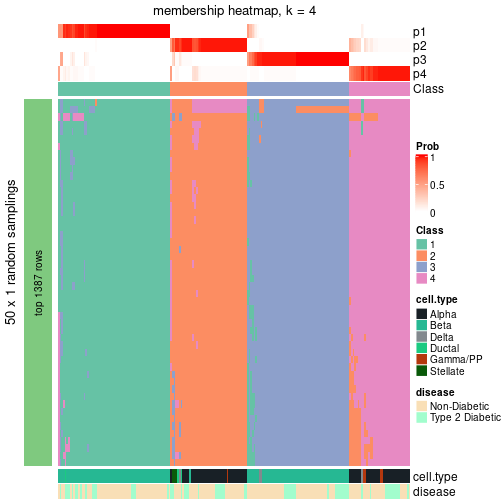
As soon as the classes for columns are determined, the signatures that are significantly different between subgroups can be looked for. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
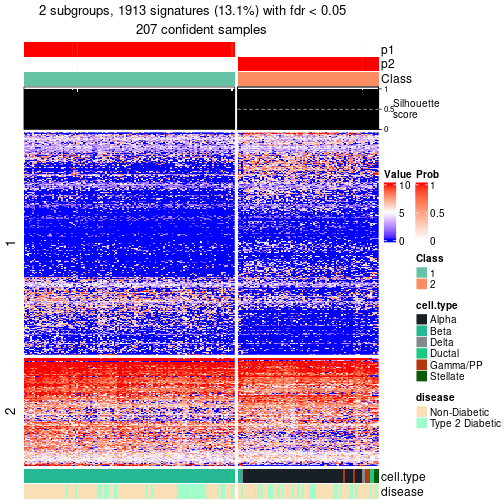
get_signatures(res, k = 3, scale_rows = FALSE)
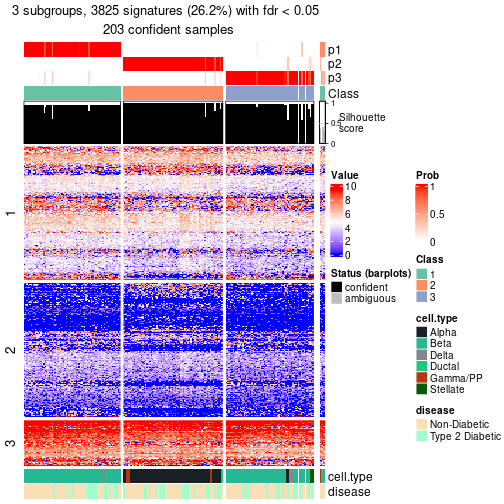
get_signatures(res, k = 4, scale_rows = FALSE)
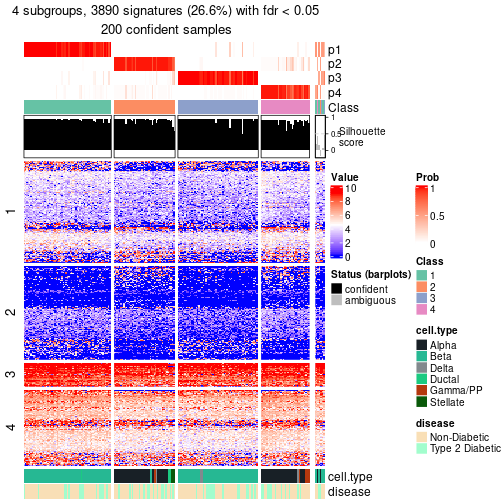
Compare the overlap of signatures from different k:
compare_signatures(res)
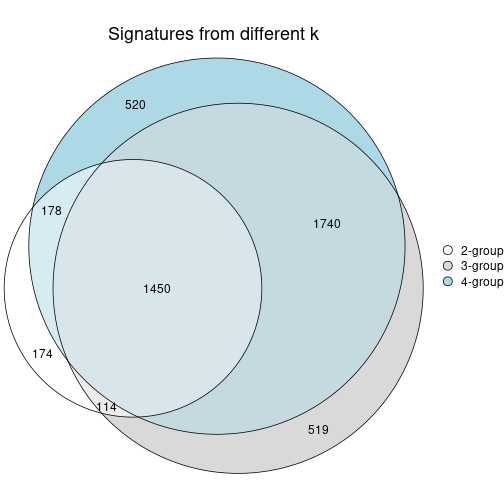
get_signature() returns a data frame invisibly. To get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows (which is done by automatically selecting number of clusters).If there are too many signatures, top_signatures = ... can be set to only show the
signatures with the highest FDRs:
# code only for demonstration
# e.g. to show the top 500 most significant rows
tb = get_signature(res, k = ..., top_signatures = 500)
If the signatures are defined as these which are uniquely high in current group, diff_method argument
can be set to "uniquely_high_in_one_group":
# code only for demonstration
tb = get_signature(res, k = ..., diff_method = "uniquely_high_in_one_group")
UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
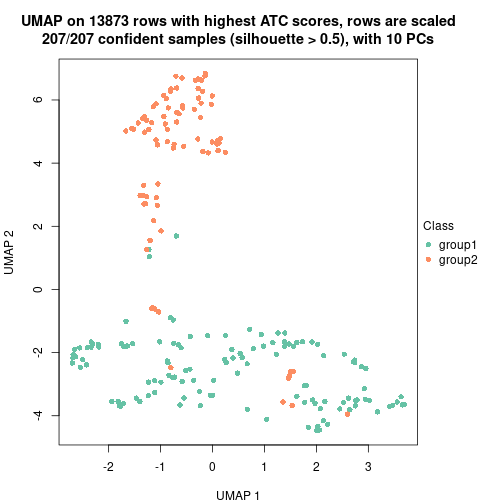
dimension_reduction(res, k = 3, method = "UMAP")
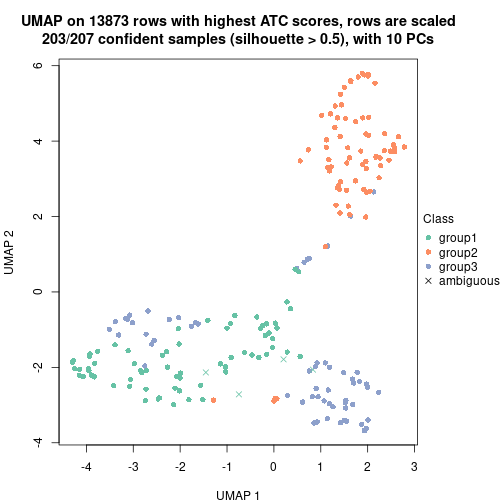
dimension_reduction(res, k = 4, method = "UMAP")
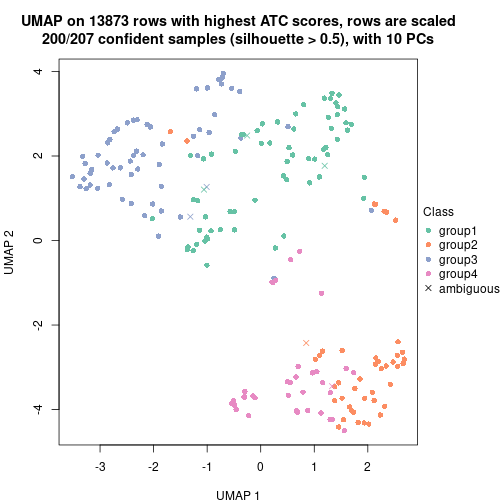
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
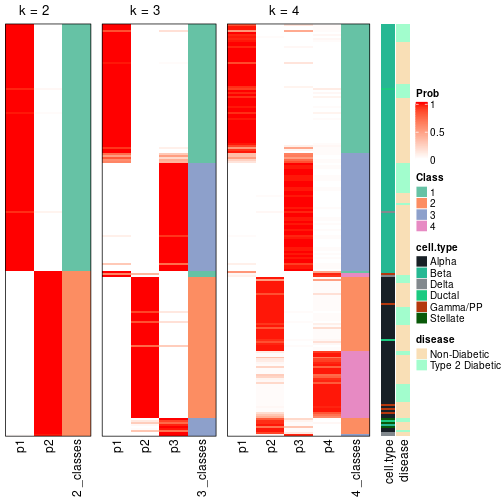
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n_sample cell.type(p-value) disease(p-value) k
#> ATC:skmeans 207 9.33e-40 0.372 2
#> ATC:skmeans 203 2.32e-37 0.584 3
#> ATC:skmeans 200 9.66e-36 0.678 4
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
Parent node: Node011. Child nodes: Node01111-leaf , Node01112-leaf , Node01121-leaf , Node01122-leaf , Node01131-leaf , Node01132 , Node01221-leaf , Node01222-leaf , Node01223-leaf , Node01231-leaf , Node01232-leaf .
The object with results only for a single top-value method and a single partitioning method can be extracted as:
res = res_rh["0111"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4.
#> On a matrix with 13816 rows and 73 columns.
#> Top rows (1382) are extracted by 'ATC' method.
#> Subgroups are detected by 'skmeans' method.
#> Performed in total 150 partitions by row resampling.
#> Best k for subgroups seems to be 2.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_partitions"
#> [7] "compare_signatures" "consensus_heatmap" "dimension_reduction"
#> [10] "functional_enrichment" "get_anno_col" "get_anno"
#> [13] "get_classes" "get_consensus" "get_matrix"
#> [16] "get_membership" "get_param" "get_signatures"
#> [19] "get_stats" "is_best_k" "is_stable_k"
#> [22] "membership_heatmap" "ncol" "nrow"
#> [25] "plot_ecdf" "predict_classes" "rownames"
#> [28] "select_partition_number" "show" "suggest_best_k"
#> [31] "test_to_known_factors" "top_rows_heatmap"
collect_plots() function collects all the plots made from res for all k (number of subgroups)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
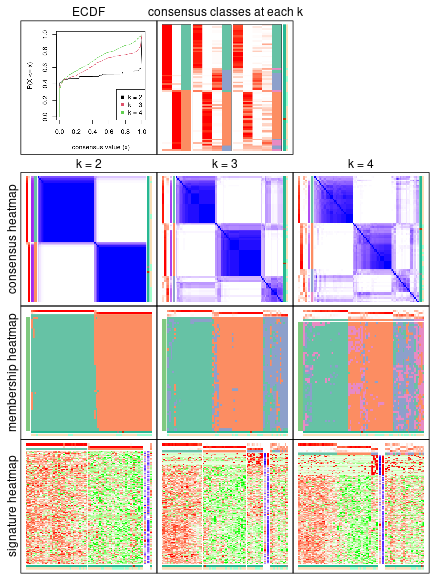
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, higher 1-PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
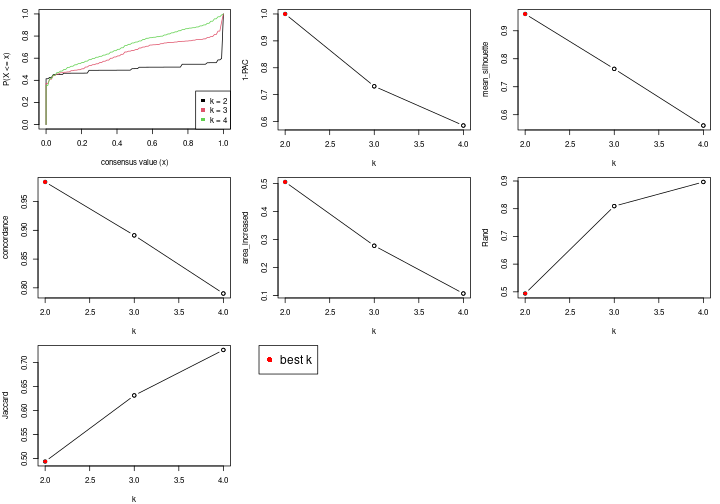
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 1.000 0.960 0.984 0.506 0.494 0.494
#> 3 3 0.731 0.764 0.891 0.278 0.809 0.632
#> 4 4 0.585 0.561 0.790 0.107 0.896 0.726
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 2
Following is the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall subgroup
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> 10th_C13_S61 2 0.000 0.9773 0.00 1.00
#> 11th-C66_S88 2 0.000 0.9773 0.00 1.00
#> 12th-C59_S169 2 0.000 0.9773 0.00 1.00
#> 12th-C60_S176 2 0.000 0.9773 0.00 1.00
#> 12th-C64_S163 2 0.000 0.9773 0.00 1.00
#> 12th-C74_S214 2 0.000 0.9773 0.00 1.00
#> 12th-C76_S177 2 0.000 0.9773 0.00 1.00
#> 12th-C84_S165 2 0.000 0.9773 0.00 1.00
#> 12th-C96_S167 2 0.000 0.9773 0.00 1.00
#> 1st-61_S27 1 0.000 0.9889 1.00 0.00
#> 1st-C11_S58 2 0.000 0.9773 0.00 1.00
#> 1st-C58_S76 1 0.000 0.9889 1.00 0.00
#> 1st-C64_S79 2 0.000 0.9773 0.00 1.00
#> 1st-C90_S91 2 0.000 0.9773 0.00 1.00
#> 2nd-C15_S25 2 0.795 0.6827 0.24 0.76
#> 2nd-C17_S32 2 0.000 0.9773 0.00 1.00
#> 2nd-C32_S62 2 0.000 0.9773 0.00 1.00
#> 2nd-C38_S74 2 0.000 0.9773 0.00 1.00
#> 2nd-C62_S29 1 0.000 0.9889 1.00 0.00
#> 2nd-C72_S48 2 0.000 0.9773 0.00 1.00
#> 2nd-C88_S84 2 0.000 0.9773 0.00 1.00
#> 2nd-C93_S88 2 0.242 0.9400 0.04 0.96
#> 3rd-C11_S58 1 0.000 0.9889 1.00 0.00
#> 3rd-C33_S50 1 0.000 0.9889 1.00 0.00
#> 3rd-C36_S2 1 0.000 0.9889 1.00 0.00
#> 3rd-C4_S25 1 0.000 0.9889 1.00 0.00
#> 3rd-C53_S67 2 0.000 0.9773 0.00 1.00
#> 3rd-C58_S3 1 0.000 0.9889 1.00 0.00
#> 3rd-C59_S91 1 0.000 0.9889 1.00 0.00
#> 3rd-C71_S80 1 0.000 0.9889 1.00 0.00
#> 3rd-C82_S11 1 0.469 0.8856 0.90 0.10
#> 3rd-C84_S75 1 0.000 0.9889 1.00 0.00
#> 3rd-C88_S24 1 0.000 0.9889 1.00 0.00
#> 3rd-C92_S86 1 0.000 0.9889 1.00 0.00
#> 4th-61_S28 1 0.000 0.9889 1.00 0.00
#> 4th-C14_S26 1 0.000 0.9889 1.00 0.00
#> 4th-C24_S43 2 0.000 0.9773 0.00 1.00
#> 4th-C26_S50 1 0.000 0.9889 1.00 0.00
#> 4th-C5_S8 2 0.000 0.9773 0.00 1.00
#> 4th-C7_S15 1 0.141 0.9712 0.98 0.02
#> 4th-C85_S78 2 0.000 0.9773 0.00 1.00
#> 4th-C89_S83 2 0.000 0.9773 0.00 1.00
#> 5th-C49_S89 1 0.000 0.9889 1.00 0.00
#> 5th-C5_S85 1 0.795 0.6784 0.76 0.24
#> 5th-C7_S93 1 0.000 0.9889 1.00 0.00
#> 6th-C12_S18 1 0.000 0.9889 1.00 0.00
#> 6th-C23_S38 1 0.000 0.9889 1.00 0.00
#> 6th-C29_S50 2 0.000 0.9773 0.00 1.00
#> 6th-C54_S11 1 0.000 0.9889 1.00 0.00
#> 6th-C59_S21 1 0.000 0.9889 1.00 0.00
#> 6th-C63_S26 1 0.000 0.9889 1.00 0.00
#> 6th-C71_S41 2 0.000 0.9773 0.00 1.00
#> 6th-C77_S53 1 0.000 0.9889 1.00 0.00
#> 6th-C79_S60 2 0.000 0.9773 0.00 1.00
#> 6th-C85_S72 2 0.000 0.9773 0.00 1.00
#> 7th-C25_S43 1 0.000 0.9889 1.00 0.00
#> 7th-C45_S77 2 0.999 0.0732 0.48 0.52
#> 7th-C53_S10 1 0.000 0.9889 1.00 0.00
#> 7th-C59_S21 1 0.000 0.9889 1.00 0.00
#> 7th-C62_S27 2 0.000 0.9773 0.00 1.00
#> 7th-C64_S31 1 0.000 0.9889 1.00 0.00
#> 7th-C77_S51 1 0.000 0.9889 1.00 0.00
#> 7th-C84_S62 1 0.000 0.9889 1.00 0.00
#> 7th-C8_S13 1 0.000 0.9889 1.00 0.00
#> 7th-C90_S73 1 0.000 0.9889 1.00 0.00
#> 7th-C96_S82 1 0.000 0.9889 1.00 0.00
#> 8th-C10_S100 1 0.000 0.9889 1.00 0.00
#> 8th-C24_S120 2 0.000 0.9773 0.00 1.00
#> 8th-C2_S85 1 0.242 0.9528 0.96 0.04
#> 8th-C65_S113 2 0.000 0.9773 0.00 1.00
#> 8th-C87_S148 2 0.000 0.9773 0.00 1.00
#> 9th-C41_S70 2 0.000 0.9773 0.00 1.00
#> 9th-C70_S42 2 0.000 0.9773 0.00 1.00
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> 10th_C13_S61 2 0.0892 0.9011 0.00 0.98 0.02
#> 11th-C66_S88 2 0.0000 0.9120 0.00 1.00 0.00
#> 12th-C59_S169 2 0.0000 0.9120 0.00 1.00 0.00
#> 12th-C60_S176 3 0.6387 0.4432 0.02 0.30 0.68
#> 12th-C64_S163 2 0.0000 0.9120 0.00 1.00 0.00
#> 12th-C74_S214 2 0.1529 0.8888 0.00 0.96 0.04
#> 12th-C76_S177 2 0.2959 0.8320 0.00 0.90 0.10
#> 12th-C84_S165 2 0.0000 0.9120 0.00 1.00 0.00
#> 12th-C96_S167 2 0.6192 0.2774 0.00 0.58 0.42
#> 1st-61_S27 1 0.0892 0.9013 0.98 0.00 0.02
#> 1st-C11_S58 2 0.0000 0.9120 0.00 1.00 0.00
#> 1st-C58_S76 3 0.4555 0.6828 0.20 0.00 0.80
#> 1st-C64_S79 2 0.6302 0.0880 0.00 0.52 0.48
#> 1st-C90_S91 2 0.2066 0.8753 0.00 0.94 0.06
#> 2nd-C15_S25 1 0.7523 0.3848 0.66 0.26 0.08
#> 2nd-C17_S32 2 0.0000 0.9120 0.00 1.00 0.00
#> 2nd-C32_S62 2 0.0892 0.9059 0.00 0.98 0.02
#> 2nd-C38_S74 2 0.0892 0.9059 0.00 0.98 0.02
#> 2nd-C62_S29 1 0.3340 0.8227 0.88 0.00 0.12
#> 2nd-C72_S48 2 0.0000 0.9120 0.00 1.00 0.00
#> 2nd-C88_S84 2 0.1529 0.8945 0.00 0.96 0.04
#> 2nd-C93_S88 2 0.9444 -0.0540 0.38 0.44 0.18
#> 3rd-C11_S58 1 0.0000 0.9138 1.00 0.00 0.00
#> 3rd-C33_S50 1 0.0892 0.9188 0.98 0.00 0.02
#> 3rd-C36_S2 1 0.0892 0.9068 0.98 0.00 0.02
#> 3rd-C4_S25 1 0.0000 0.9138 1.00 0.00 0.00
#> 3rd-C53_S67 2 0.0000 0.9120 0.00 1.00 0.00
#> 3rd-C58_S3 1 0.0000 0.9138 1.00 0.00 0.00
#> 3rd-C59_S91 1 0.0000 0.9138 1.00 0.00 0.00
#> 3rd-C71_S80 1 0.0000 0.9138 1.00 0.00 0.00
#> 3rd-C82_S11 3 0.0892 0.7158 0.00 0.02 0.98
#> 3rd-C84_S75 1 0.1529 0.9069 0.96 0.00 0.04
#> 3rd-C88_S24 1 0.0892 0.9188 0.98 0.00 0.02
#> 3rd-C92_S86 1 0.2066 0.8672 0.94 0.00 0.06
#> 4th-61_S28 3 0.4796 0.6771 0.22 0.00 0.78
#> 4th-C14_S26 1 0.6984 0.0701 0.56 0.02 0.42
#> 4th-C24_S43 2 0.0000 0.9120 0.00 1.00 0.00
#> 4th-C26_S50 3 0.1529 0.7207 0.04 0.00 0.96
#> 4th-C5_S8 3 0.6192 0.1983 0.00 0.42 0.58
#> 4th-C7_S15 3 0.0892 0.7200 0.02 0.00 0.98
#> 4th-C85_S78 2 0.6302 0.0624 0.00 0.52 0.48
#> 4th-C89_S83 2 0.0000 0.9120 0.00 1.00 0.00
#> 5th-C49_S89 3 0.5835 0.5433 0.34 0.00 0.66
#> 5th-C5_S85 3 0.6109 0.7042 0.14 0.08 0.78
#> 5th-C7_S93 3 0.6192 0.4009 0.42 0.00 0.58
#> 6th-C12_S18 1 0.0892 0.9188 0.98 0.00 0.02
#> 6th-C23_S38 1 0.5397 0.5545 0.72 0.00 0.28
#> 6th-C29_S50 2 0.0892 0.9059 0.00 0.98 0.02
#> 6th-C54_S11 1 0.0892 0.9188 0.98 0.00 0.02
#> 6th-C59_S21 1 0.4291 0.7209 0.82 0.00 0.18
#> 6th-C63_S26 3 0.5948 0.5194 0.36 0.00 0.64
#> 6th-C71_S41 2 0.0892 0.9059 0.00 0.98 0.02
#> 6th-C77_S53 1 0.0892 0.9188 0.98 0.00 0.02
#> 6th-C79_S60 2 0.0000 0.9120 0.00 1.00 0.00
#> 6th-C85_S72 2 0.0000 0.9120 0.00 1.00 0.00
#> 7th-C25_S43 1 0.0892 0.9188 0.98 0.00 0.02
#> 7th-C45_S77 3 0.9602 0.3800 0.22 0.32 0.46
#> 7th-C53_S10 1 0.0892 0.9188 0.98 0.00 0.02
#> 7th-C59_S21 1 0.0892 0.9188 0.98 0.00 0.02
#> 7th-C62_S27 2 0.2414 0.8727 0.04 0.94 0.02
#> 7th-C64_S31 1 0.0892 0.9188 0.98 0.00 0.02
#> 7th-C77_S51 1 0.0892 0.9188 0.98 0.00 0.02
#> 7th-C84_S62 1 0.1529 0.9069 0.96 0.00 0.04
#> 7th-C8_S13 1 0.0000 0.9138 1.00 0.00 0.00
#> 7th-C90_S73 3 0.4555 0.6873 0.20 0.00 0.80
#> 7th-C96_S82 1 0.0892 0.9188 0.98 0.00 0.02
#> 8th-C10_S100 3 0.6280 0.2603 0.46 0.00 0.54
#> 8th-C24_S120 2 0.0892 0.9059 0.00 0.98 0.02
#> 8th-C2_S85 3 0.0892 0.7200 0.02 0.00 0.98
#> 8th-C65_S113 2 0.0000 0.9120 0.00 1.00 0.00
#> 8th-C87_S148 2 0.0892 0.9059 0.00 0.98 0.02
#> 9th-C41_S70 2 0.0000 0.9120 0.00 1.00 0.00
#> 9th-C70_S42 2 0.0000 0.9120 0.00 1.00 0.00
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> 10th_C13_S61 2 0.1913 0.74509 0.00 0.94 0.04 0.02
#> 11th-C66_S88 2 0.0707 0.76616 0.00 0.98 0.00 0.02
#> 12th-C59_S169 2 0.0000 0.76701 0.00 1.00 0.00 0.00
#> 12th-C60_S176 3 0.7602 0.08817 0.00 0.38 0.42 0.20
#> 12th-C64_S163 2 0.0707 0.76616 0.00 0.98 0.00 0.02
#> 12th-C74_S214 2 0.1913 0.74487 0.00 0.94 0.04 0.02
#> 12th-C76_S177 2 0.6714 0.24177 0.00 0.54 0.10 0.36
#> 12th-C84_S165 2 0.0000 0.76701 0.00 1.00 0.00 0.00
#> 12th-C96_S167 2 0.6110 0.40622 0.00 0.66 0.24 0.10
#> 1st-61_S27 1 0.2921 0.80953 0.86 0.00 0.00 0.14
#> 1st-C11_S58 2 0.1637 0.75502 0.00 0.94 0.00 0.06
#> 1st-C58_S76 3 0.5383 0.49014 0.10 0.00 0.74 0.16
#> 1st-C64_S79 2 0.7707 -0.06290 0.00 0.44 0.32 0.24
#> 1st-C90_S91 2 0.4936 0.53753 0.00 0.70 0.02 0.28
#> 2nd-C15_S25 4 0.6835 0.26283 0.38 0.06 0.02 0.54
#> 2nd-C17_S32 2 0.2345 0.73798 0.00 0.90 0.00 0.10
#> 2nd-C32_S62 2 0.4948 0.27986 0.00 0.56 0.00 0.44
#> 2nd-C38_S74 2 0.4134 0.59615 0.00 0.74 0.00 0.26
#> 2nd-C62_S29 1 0.2647 0.79470 0.88 0.00 0.12 0.00
#> 2nd-C72_S48 2 0.0000 0.76701 0.00 1.00 0.00 0.00
#> 2nd-C88_S84 4 0.4994 -0.24466 0.00 0.48 0.00 0.52
#> 2nd-C93_S88 4 0.5284 0.33901 0.10 0.10 0.02 0.78
#> 3rd-C11_S58 1 0.2706 0.82566 0.90 0.00 0.02 0.08
#> 3rd-C33_S50 1 0.0707 0.85773 0.98 0.00 0.02 0.00
#> 3rd-C36_S2 1 0.1411 0.85459 0.96 0.00 0.02 0.02
#> 3rd-C4_S25 1 0.1211 0.85176 0.96 0.00 0.00 0.04
#> 3rd-C53_S67 2 0.6005 0.16048 0.00 0.50 0.04 0.46
#> 3rd-C58_S3 1 0.3606 0.77145 0.84 0.00 0.02 0.14
#> 3rd-C59_S91 1 0.2335 0.83725 0.92 0.00 0.02 0.06
#> 3rd-C71_S80 1 0.1211 0.85176 0.96 0.00 0.00 0.04
#> 3rd-C82_S11 3 0.5765 0.47743 0.04 0.02 0.70 0.24
#> 3rd-C84_S75 1 0.1211 0.84821 0.96 0.00 0.04 0.00
#> 3rd-C88_S24 1 0.0000 0.85812 1.00 0.00 0.00 0.00
#> 3rd-C92_S86 1 0.4948 0.20445 0.56 0.00 0.00 0.44
#> 4th-61_S28 3 0.5489 0.46394 0.24 0.00 0.70 0.06
#> 4th-C14_S26 4 0.7581 -0.04322 0.36 0.00 0.20 0.44
#> 4th-C24_S43 2 0.1211 0.76104 0.00 0.96 0.00 0.04
#> 4th-C26_S50 3 0.4079 0.52180 0.02 0.00 0.80 0.18
#> 4th-C5_S8 3 0.7877 0.07650 0.00 0.36 0.36 0.28
#> 4th-C7_S15 3 0.3030 0.54787 0.02 0.02 0.90 0.06
#> 4th-C85_S78 3 0.7845 0.00461 0.00 0.32 0.40 0.28
#> 4th-C89_S83 2 0.0707 0.76616 0.00 0.98 0.00 0.02
#> 5th-C49_S89 3 0.6453 0.32727 0.36 0.00 0.56 0.08
#> 5th-C5_S85 3 0.5422 0.50345 0.04 0.02 0.74 0.20
#> 5th-C7_S93 1 0.5594 0.04408 0.52 0.00 0.46 0.02
#> 6th-C12_S18 1 0.1913 0.84399 0.94 0.00 0.02 0.04
#> 6th-C23_S38 1 0.6122 0.56911 0.68 0.00 0.16 0.16
#> 6th-C29_S50 2 0.3801 0.64231 0.00 0.78 0.00 0.22
#> 6th-C54_S11 1 0.1211 0.84903 0.96 0.00 0.04 0.00
#> 6th-C59_S21 1 0.5256 0.57157 0.70 0.00 0.26 0.04
#> 6th-C63_S26 3 0.6605 0.07907 0.44 0.00 0.48 0.08
#> 6th-C71_S41 2 0.3975 0.62082 0.00 0.76 0.00 0.24
#> 6th-C77_S53 1 0.0000 0.85812 1.00 0.00 0.00 0.00
#> 6th-C79_S60 2 0.0000 0.76701 0.00 1.00 0.00 0.00
#> 6th-C85_S72 2 0.1211 0.75864 0.00 0.96 0.00 0.04
#> 7th-C25_S43 1 0.0000 0.85812 1.00 0.00 0.00 0.00
#> 7th-C45_S77 4 0.9567 0.08100 0.14 0.22 0.26 0.38
#> 7th-C53_S10 1 0.1913 0.85200 0.94 0.00 0.02 0.04
#> 7th-C59_S21 1 0.0000 0.85812 1.00 0.00 0.00 0.00
#> 7th-C62_S27 2 0.5570 0.23619 0.02 0.54 0.00 0.44
#> 7th-C64_S31 1 0.0000 0.85812 1.00 0.00 0.00 0.00
#> 7th-C77_S51 1 0.0707 0.85671 0.98 0.00 0.00 0.02
#> 7th-C84_S62 1 0.1637 0.83946 0.94 0.00 0.06 0.00
#> 7th-C8_S13 1 0.2011 0.84315 0.92 0.00 0.00 0.08
#> 7th-C90_S73 3 0.5962 0.44622 0.26 0.00 0.66 0.08
#> 7th-C96_S82 1 0.0707 0.85686 0.98 0.00 0.00 0.02
#> 8th-C10_S100 1 0.7499 -0.10593 0.42 0.00 0.40 0.18
#> 8th-C24_S120 2 0.3610 0.66186 0.00 0.80 0.00 0.20
#> 8th-C2_S85 3 0.2335 0.54876 0.02 0.00 0.92 0.06
#> 8th-C65_S113 2 0.0000 0.76701 0.00 1.00 0.00 0.00
#> 8th-C87_S148 4 0.5594 -0.17090 0.00 0.46 0.02 0.52
#> 9th-C41_S70 2 0.0707 0.76645 0.00 0.98 0.00 0.02
#> 9th-C70_S42 2 0.3801 0.64202 0.00 0.78 0.00 0.22
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
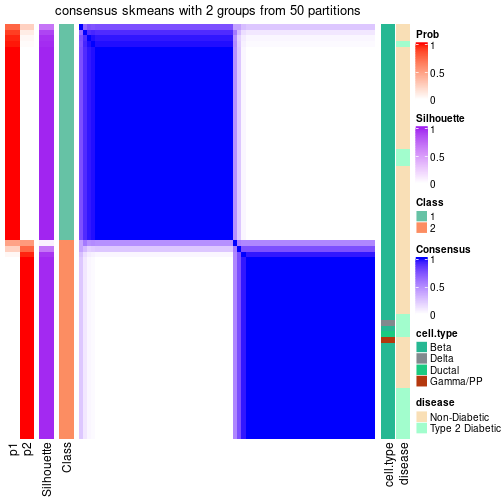
consensus_heatmap(res, k = 3)
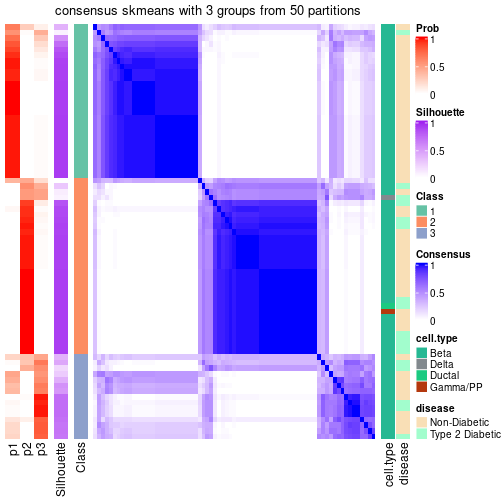
consensus_heatmap(res, k = 4)
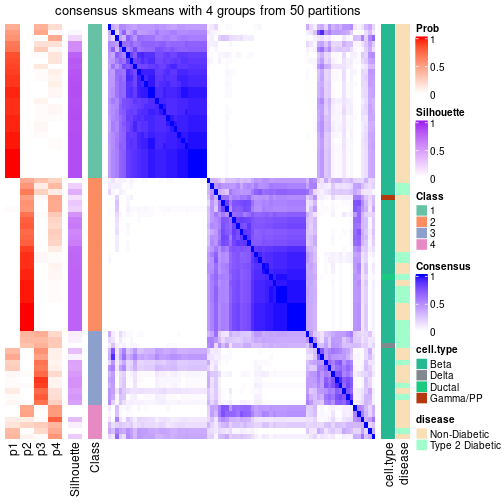
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
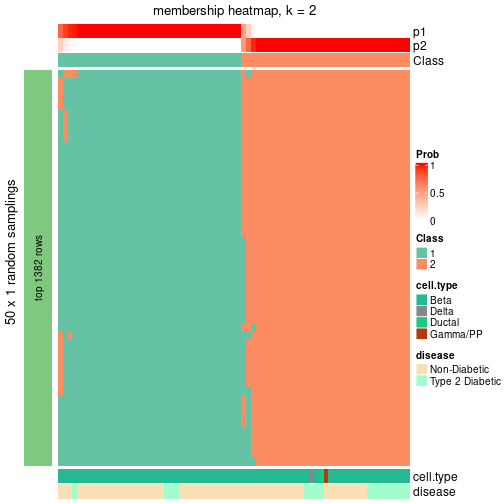
membership_heatmap(res, k = 3)

membership_heatmap(res, k = 4)
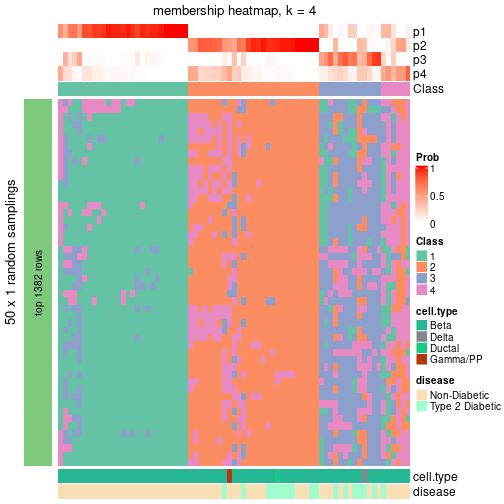
As soon as the classes for columns are determined, the signatures that are significantly different between subgroups can be looked for. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
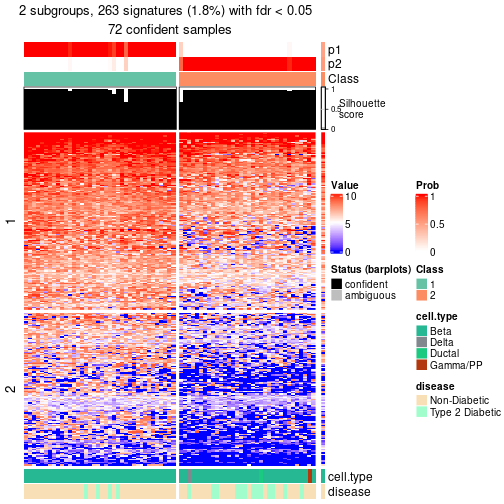
get_signatures(res, k = 3, scale_rows = FALSE)
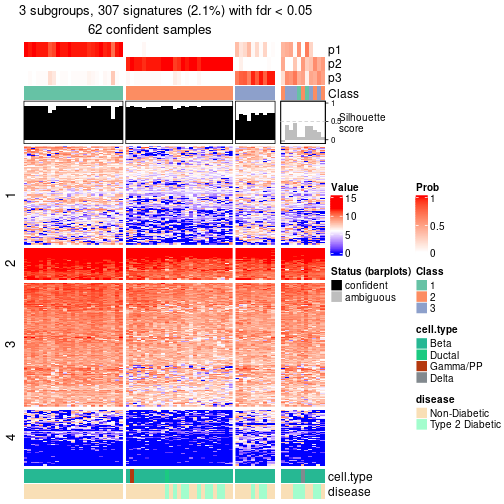
get_signatures(res, k = 4, scale_rows = FALSE)
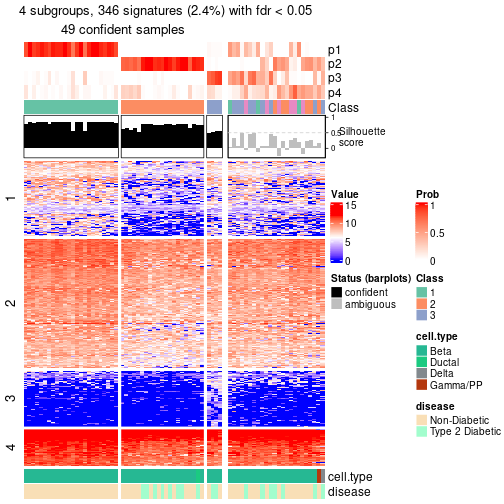
Compare the overlap of signatures from different k:
compare_signatures(res)
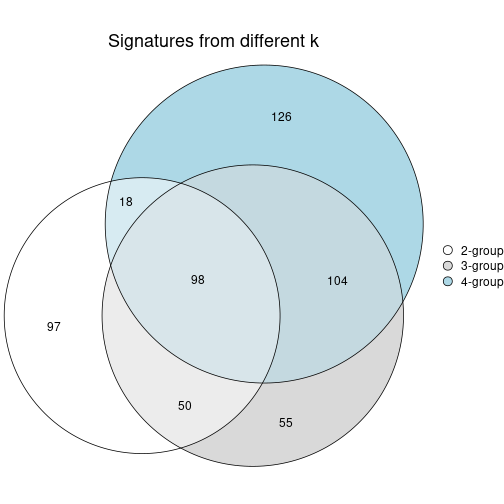
get_signature() returns a data frame invisibly. To get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows (which is done by automatically selecting number of clusters).If there are too many signatures, top_signatures = ... can be set to only show the
signatures with the highest FDRs:
# code only for demonstration
# e.g. to show the top 500 most significant rows
tb = get_signature(res, k = ..., top_signatures = 500)
If the signatures are defined as these which are uniquely high in current group, diff_method argument
can be set to "uniquely_high_in_one_group":
# code only for demonstration
tb = get_signature(res, k = ..., diff_method = "uniquely_high_in_one_group")
UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
dimension_reduction(res, k = 3, method = "UMAP")
dimension_reduction(res, k = 4, method = "UMAP")
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
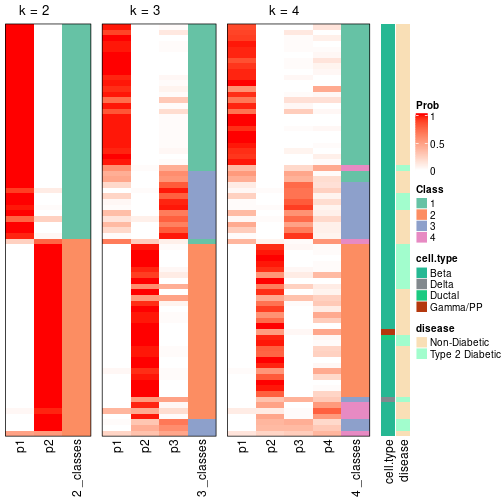
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n_sample cell.type(p-value) disease(p-value) k
#> ATC:skmeans 72 0.321 0.01292 2
#> ATC:skmeans 62 0.613 0.00639 3
#> ATC:skmeans 49 0.506 0.00208 4
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
Parent node: Node011. Child nodes: Node01111-leaf , Node01112-leaf , Node01121-leaf , Node01122-leaf , Node01131-leaf , Node01132 , Node01221-leaf , Node01222-leaf , Node01223-leaf , Node01231-leaf , Node01232-leaf .
The object with results only for a single top-value method and a single partitioning method can be extracted as:
res = res_rh["0112"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4.
#> On a matrix with 13836 rows and 71 columns.
#> Top rows (1384) are extracted by 'ATC' method.
#> Subgroups are detected by 'skmeans' method.
#> Performed in total 150 partitions by row resampling.
#> Best k for subgroups seems to be 2.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_partitions"
#> [7] "compare_signatures" "consensus_heatmap" "dimension_reduction"
#> [10] "functional_enrichment" "get_anno_col" "get_anno"
#> [13] "get_classes" "get_consensus" "get_matrix"
#> [16] "get_membership" "get_param" "get_signatures"
#> [19] "get_stats" "is_best_k" "is_stable_k"
#> [22] "membership_heatmap" "ncol" "nrow"
#> [25] "plot_ecdf" "predict_classes" "rownames"
#> [28] "select_partition_number" "show" "suggest_best_k"
#> [31] "test_to_known_factors" "top_rows_heatmap"
collect_plots() function collects all the plots made from res for all k (number of subgroups)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
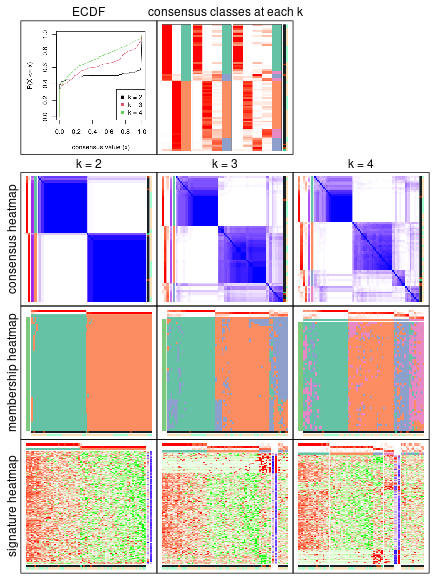
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, higher 1-PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
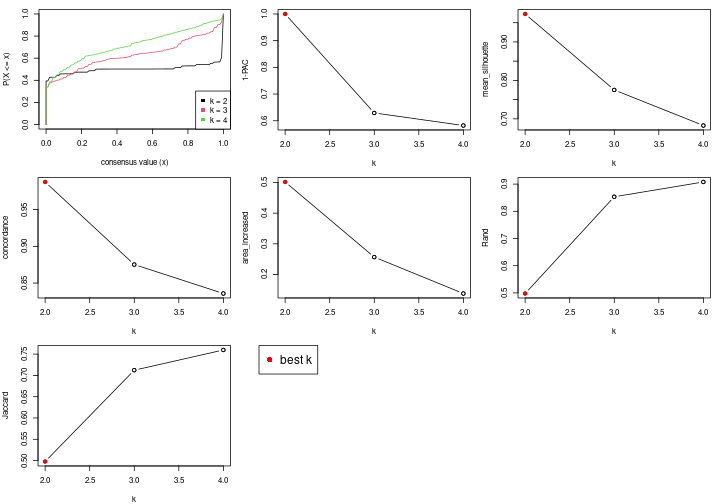
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 1.000 0.973 0.988 0.502 0.498 0.498
#> 3 3 0.629 0.775 0.875 0.257 0.854 0.712
#> 4 4 0.582 0.683 0.836 0.138 0.908 0.760
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 2
Following is the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall subgroup
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> 12th-C29_S150 2 0.000 0.992 0.00 1.00
#> 12th-C58_S162 1 0.000 0.981 1.00 0.00
#> 12th-C95_S174 1 0.000 0.981 1.00 0.00
#> 13th_C66_S214 2 0.000 0.992 0.00 1.00
#> 13th_C76_S216 2 0.000 0.992 0.00 1.00
#> 1st-C19_S20 2 0.000 0.992 0.00 1.00
#> 1st-C50_S33 2 0.000 0.992 0.00 1.00
#> 1st-C56_S34 1 0.000 0.981 1.00 0.00
#> 1st-C57_S42 2 0.000 0.992 0.00 1.00
#> 1st-C68_S36 1 0.402 0.909 0.92 0.08
#> 1st-C73_S45 2 0.000 0.992 0.00 1.00
#> 1st-C75_S29 2 0.141 0.974 0.02 0.98
#> 1st-C78_S85 2 0.000 0.992 0.00 1.00
#> 1st-C80_S38 1 0.000 0.981 1.00 0.00
#> 2nd-C11_S20 1 0.000 0.981 1.00 0.00
#> 2nd-C16_S33 1 0.000 0.981 1.00 0.00
#> 2nd-C26_S50 1 0.000 0.981 1.00 0.00
#> 2nd-C39_S75 1 0.000 0.981 1.00 0.00
#> 2nd-C67_S40 2 0.000 0.992 0.00 1.00
#> 2nd-C75_S52 1 0.000 0.981 1.00 0.00
#> 2nd-C77_S59 2 0.000 0.992 0.00 1.00
#> 2nd-C80_S65 1 0.000 0.981 1.00 0.00
#> 2nd-C8_S14 2 0.141 0.974 0.02 0.98
#> 3rd-C12_S68 2 0.000 0.992 0.00 1.00
#> 3rd-C27_S49 2 0.000 0.992 0.00 1.00
#> 3rd-C47_S35 2 0.000 0.992 0.00 1.00
#> 3rd-C49_S60 2 0.000 0.992 0.00 1.00
#> 3rd-C57_S5 1 0.855 0.621 0.72 0.28
#> 3rd-C79_S67 1 0.000 0.981 1.00 0.00
#> 3rd-C85_S79 1 0.000 0.981 1.00 0.00
#> 3rd-C91_S91 1 0.000 0.981 1.00 0.00
#> 3rd-C95_S81 1 0.000 0.981 1.00 0.00
#> 4th-C18_S31 2 0.000 0.992 0.00 1.00
#> 4th-C40_S79 1 0.000 0.981 1.00 0.00
#> 4th-C4_S9 2 0.000 0.992 0.00 1.00
#> 4th-C56_S17 2 0.000 0.992 0.00 1.00
#> 4th-C62_S29 1 0.000 0.981 1.00 0.00
#> 4th-C64_S34 1 0.000 0.981 1.00 0.00
#> 4th-C66_S36 1 0.000 0.981 1.00 0.00
#> 4th-C73_S54 2 0.000 0.992 0.00 1.00
#> 4th-C75_S52 2 0.000 0.992 0.00 1.00
#> 4th-C79_S66 2 0.000 0.992 0.00 1.00
#> 4th-C80_S65 1 0.000 0.981 1.00 0.00
#> 4th-C82_S72 1 0.000 0.981 1.00 0.00
#> 4th-C83_S71 2 0.000 0.992 0.00 1.00
#> 4th-C86_S77 1 0.000 0.981 1.00 0.00
#> 4th-C88_S84 1 0.000 0.981 1.00 0.00
#> 4th-C92_S89 1 0.000 0.981 1.00 0.00
#> 4th-C94_S96 2 0.000 0.992 0.00 1.00
#> 4th-C96_S94 2 0.000 0.992 0.00 1.00
#> 5th-C34_S108 1 0.000 0.981 1.00 0.00
#> 5th-C9_S92 1 0.000 0.981 1.00 0.00
#> 6th-C21_S33 2 0.000 0.992 0.00 1.00
#> 6th-C87_S70 2 0.000 0.992 0.00 1.00
#> 7th-C11_S18 2 0.000 0.992 0.00 1.00
#> 7th-C14_S24 1 0.000 0.981 1.00 0.00
#> 7th-C24_S40 1 0.634 0.812 0.84 0.16
#> 7th-C36_S61 2 0.000 0.992 0.00 1.00
#> 7th-C58_S20 1 0.000 0.981 1.00 0.00
#> 7th-C79_S58 2 0.000 0.992 0.00 1.00
#> 7th-C82_S64 2 0.141 0.974 0.02 0.98
#> 8th-C55_S96 2 0.000 0.992 0.00 1.00
#> 8th-C57_S98 2 0.000 0.992 0.00 1.00
#> 8th-C58_S101 1 0.327 0.929 0.94 0.06
#> 8th-C67_S117 2 0.795 0.681 0.24 0.76
#> 8th-C74_S129 2 0.000 0.992 0.00 1.00
#> 8th-C85_S150 2 0.000 0.992 0.00 1.00
#> 9th-C57_S16 2 0.000 0.992 0.00 1.00
#> 9th-C80_S56 2 0.000 0.992 0.00 1.00
#> 9th-C83_S61 1 0.000 0.981 1.00 0.00
#> 9th-C9_S13 2 0.000 0.992 0.00 1.00
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> 12th-C29_S150 3 0.6280 0.384 0.00 0.46 0.54
#> 12th-C58_S162 1 0.5216 0.649 0.74 0.00 0.26
#> 12th-C95_S174 1 0.0000 0.910 1.00 0.00 0.00
#> 13th_C66_S214 3 0.5016 0.692 0.00 0.24 0.76
#> 13th_C76_S216 2 0.2537 0.853 0.00 0.92 0.08
#> 1st-C19_S20 2 0.0000 0.876 0.00 1.00 0.00
#> 1st-C50_S33 2 0.5835 0.454 0.00 0.66 0.34
#> 1st-C56_S34 1 0.1529 0.890 0.96 0.00 0.04
#> 1st-C57_S42 2 0.5397 0.552 0.00 0.72 0.28
#> 1st-C68_S36 3 0.9659 0.161 0.34 0.22 0.44
#> 1st-C73_S45 2 0.2066 0.863 0.00 0.94 0.06
#> 1st-C75_S29 3 0.4862 0.701 0.02 0.16 0.82
#> 1st-C78_S85 2 0.0000 0.876 0.00 1.00 0.00
#> 1st-C80_S38 1 0.5643 0.738 0.76 0.02 0.22
#> 2nd-C11_S20 1 0.4291 0.791 0.82 0.00 0.18
#> 2nd-C16_S33 1 0.0000 0.910 1.00 0.00 0.00
#> 2nd-C26_S50 1 0.5216 0.721 0.74 0.00 0.26
#> 2nd-C39_S75 1 0.0000 0.910 1.00 0.00 0.00
#> 2nd-C67_S40 2 0.2959 0.831 0.00 0.90 0.10
#> 2nd-C75_S52 1 0.0000 0.910 1.00 0.00 0.00
#> 2nd-C77_S59 2 0.0000 0.876 0.00 1.00 0.00
#> 2nd-C80_S65 1 0.0000 0.910 1.00 0.00 0.00
#> 2nd-C8_S14 2 0.5397 0.552 0.00 0.72 0.28
#> 3rd-C12_S68 2 0.5016 0.611 0.00 0.76 0.24
#> 3rd-C27_S49 2 0.2066 0.863 0.00 0.94 0.06
#> 3rd-C47_S35 3 0.5216 0.681 0.00 0.26 0.74
#> 3rd-C49_S60 2 0.0000 0.876 0.00 1.00 0.00
#> 3rd-C57_S5 3 0.8219 0.464 0.18 0.18 0.64
#> 3rd-C79_S67 1 0.8859 0.204 0.48 0.12 0.40
#> 3rd-C85_S79 1 0.6232 0.703 0.74 0.04 0.22
#> 3rd-C91_S91 1 0.2066 0.874 0.94 0.00 0.06
#> 3rd-C95_S81 1 0.4291 0.792 0.82 0.00 0.18
#> 4th-C18_S31 2 0.1529 0.870 0.00 0.96 0.04
#> 4th-C40_S79 1 0.0000 0.910 1.00 0.00 0.00
#> 4th-C4_S9 2 0.0892 0.866 0.00 0.98 0.02
#> 4th-C56_S17 2 0.1529 0.870 0.00 0.96 0.04
#> 4th-C62_S29 1 0.0000 0.910 1.00 0.00 0.00
#> 4th-C64_S34 1 0.0000 0.910 1.00 0.00 0.00
#> 4th-C66_S36 1 0.0000 0.910 1.00 0.00 0.00
#> 4th-C73_S54 2 0.0892 0.874 0.00 0.98 0.02
#> 4th-C75_S52 2 0.2066 0.848 0.00 0.94 0.06
#> 4th-C79_S66 2 0.1529 0.870 0.00 0.96 0.04
#> 4th-C80_S65 1 0.0000 0.910 1.00 0.00 0.00
#> 4th-C82_S72 1 0.0000 0.910 1.00 0.00 0.00
#> 4th-C83_S71 2 0.0000 0.876 0.00 1.00 0.00
#> 4th-C86_S77 1 0.0000 0.910 1.00 0.00 0.00
#> 4th-C88_S84 1 0.0000 0.910 1.00 0.00 0.00
#> 4th-C92_S89 1 0.0000 0.910 1.00 0.00 0.00
#> 4th-C94_S96 2 0.0000 0.876 0.00 1.00 0.00
#> 4th-C96_S94 2 0.4555 0.713 0.00 0.80 0.20
#> 5th-C34_S108 1 0.5016 0.667 0.76 0.00 0.24
#> 5th-C9_S92 1 0.0000 0.910 1.00 0.00 0.00
#> 6th-C21_S33 2 0.2959 0.834 0.00 0.90 0.10
#> 6th-C87_S70 3 0.6302 0.312 0.00 0.48 0.52
#> 7th-C11_S18 2 0.2066 0.863 0.00 0.94 0.06
#> 7th-C14_S24 1 0.0000 0.910 1.00 0.00 0.00
#> 7th-C24_S40 3 0.7058 0.702 0.10 0.18 0.72
#> 7th-C36_S61 2 0.0000 0.876 0.00 1.00 0.00
#> 7th-C58_S20 1 0.0000 0.910 1.00 0.00 0.00
#> 7th-C79_S58 2 0.0000 0.876 0.00 1.00 0.00
#> 7th-C82_S64 3 0.6053 0.684 0.02 0.26 0.72
#> 8th-C55_S96 2 0.5016 0.606 0.00 0.76 0.24
#> 8th-C57_S98 2 0.2066 0.863 0.00 0.94 0.06
#> 8th-C58_S101 3 0.8033 0.547 0.24 0.12 0.64
#> 8th-C67_S117 3 0.6530 0.688 0.12 0.12 0.76
#> 8th-C74_S129 2 0.5016 0.676 0.00 0.76 0.24
#> 8th-C85_S150 2 0.4555 0.694 0.00 0.80 0.20
#> 9th-C57_S16 2 0.2537 0.854 0.00 0.92 0.08
#> 9th-C80_S56 2 0.0000 0.876 0.00 1.00 0.00
#> 9th-C83_S61 1 0.2066 0.881 0.94 0.00 0.06
#> 9th-C9_S13 2 0.0892 0.874 0.00 0.98 0.02
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> 12th-C29_S150 3 0.6570 0.4800 0.00 0.32 0.58 0.10
#> 12th-C58_S162 1 0.7021 0.1895 0.48 0.00 0.40 0.12
#> 12th-C95_S174 1 0.0000 0.8392 1.00 0.00 0.00 0.00
#> 13th_C66_S214 3 0.4731 0.6615 0.00 0.16 0.78 0.06
#> 13th_C76_S216 2 0.2335 0.8604 0.00 0.92 0.02 0.06
#> 1st-C19_S20 2 0.2921 0.8281 0.00 0.86 0.00 0.14
#> 1st-C50_S33 4 0.3172 0.6249 0.00 0.16 0.00 0.84
#> 1st-C56_S34 1 0.2647 0.7600 0.88 0.00 0.00 0.12
#> 1st-C57_S42 4 0.3198 0.6305 0.00 0.08 0.04 0.88
#> 1st-C68_S36 4 0.6767 0.4746 0.22 0.04 0.08 0.66
#> 1st-C73_S45 2 0.0707 0.8578 0.00 0.98 0.02 0.00
#> 1st-C75_S29 3 0.3525 0.6601 0.00 0.04 0.86 0.10
#> 1st-C78_S85 2 0.2921 0.8353 0.00 0.86 0.00 0.14
#> 1st-C80_S38 1 0.7493 0.1851 0.48 0.00 0.20 0.32
#> 2nd-C11_S20 1 0.4790 0.4002 0.62 0.00 0.00 0.38
#> 2nd-C16_S33 1 0.0000 0.8392 1.00 0.00 0.00 0.00
#> 2nd-C26_S50 1 0.7430 0.2907 0.54 0.02 0.12 0.32
#> 2nd-C39_S75 1 0.0000 0.8392 1.00 0.00 0.00 0.00
#> 2nd-C67_S40 2 0.5902 0.6425 0.00 0.70 0.14 0.16
#> 2nd-C75_S52 1 0.0000 0.8392 1.00 0.00 0.00 0.00
#> 2nd-C77_S59 2 0.3037 0.8500 0.00 0.88 0.02 0.10
#> 2nd-C80_S65 1 0.0000 0.8392 1.00 0.00 0.00 0.00
#> 2nd-C8_S14 4 0.2011 0.6407 0.00 0.08 0.00 0.92
#> 3rd-C12_S68 4 0.3610 0.5941 0.00 0.20 0.00 0.80
#> 3rd-C27_S49 2 0.0707 0.8589 0.00 0.98 0.00 0.02
#> 3rd-C47_S35 3 0.4284 0.6581 0.00 0.20 0.78 0.02
#> 3rd-C49_S60 2 0.2011 0.8573 0.00 0.92 0.00 0.08
#> 3rd-C57_S5 4 0.6208 0.5690 0.04 0.08 0.16 0.72
#> 3rd-C79_S67 4 0.6439 0.5222 0.20 0.02 0.10 0.68
#> 3rd-C85_S79 4 0.5860 0.1627 0.38 0.00 0.04 0.58
#> 3rd-C91_S91 1 0.6700 0.5559 0.66 0.02 0.20 0.12
#> 3rd-C95_S81 1 0.6011 0.0255 0.48 0.00 0.04 0.48
#> 4th-C18_S31 2 0.0707 0.8549 0.00 0.98 0.02 0.00
#> 4th-C40_S79 1 0.0000 0.8392 1.00 0.00 0.00 0.00
#> 4th-C4_S9 2 0.5327 0.6910 0.00 0.72 0.06 0.22
#> 4th-C56_S17 2 0.0000 0.8581 0.00 1.00 0.00 0.00
#> 4th-C62_S29 1 0.0000 0.8392 1.00 0.00 0.00 0.00
#> 4th-C64_S34 1 0.0000 0.8392 1.00 0.00 0.00 0.00
#> 4th-C66_S36 1 0.0000 0.8392 1.00 0.00 0.00 0.00
#> 4th-C73_S54 2 0.4610 0.7670 0.00 0.80 0.10 0.10
#> 4th-C75_S52 2 0.5175 0.7257 0.00 0.76 0.12 0.12
#> 4th-C79_S66 2 0.1411 0.8594 0.00 0.96 0.02 0.02
#> 4th-C80_S65 1 0.0000 0.8392 1.00 0.00 0.00 0.00
#> 4th-C82_S72 1 0.0000 0.8392 1.00 0.00 0.00 0.00
#> 4th-C83_S71 2 0.4134 0.7016 0.00 0.74 0.00 0.26
#> 4th-C86_S77 1 0.0000 0.8392 1.00 0.00 0.00 0.00
#> 4th-C88_S84 1 0.0000 0.8392 1.00 0.00 0.00 0.00
#> 4th-C92_S89 1 0.0000 0.8392 1.00 0.00 0.00 0.00
#> 4th-C94_S96 2 0.2921 0.8240 0.00 0.86 0.00 0.14
#> 4th-C96_S94 4 0.7047 0.0773 0.00 0.44 0.12 0.44
#> 5th-C34_S108 1 0.4713 0.4681 0.64 0.00 0.36 0.00
#> 5th-C9_S92 1 0.0000 0.8392 1.00 0.00 0.00 0.00
#> 6th-C21_S33 2 0.1637 0.8510 0.00 0.94 0.06 0.00
#> 6th-C87_S70 3 0.5487 0.3610 0.00 0.40 0.58 0.02
#> 7th-C11_S18 2 0.1211 0.8615 0.00 0.96 0.00 0.04
#> 7th-C14_S24 1 0.2411 0.7993 0.92 0.00 0.04 0.04
#> 7th-C24_S40 3 0.0000 0.6785 0.00 0.00 1.00 0.00
#> 7th-C36_S61 2 0.3606 0.8238 0.00 0.84 0.02 0.14
#> 7th-C58_S20 1 0.0707 0.8285 0.98 0.00 0.00 0.02
#> 7th-C79_S58 2 0.3400 0.8003 0.00 0.82 0.00 0.18
#> 7th-C82_S64 3 0.0000 0.6785 0.00 0.00 1.00 0.00
#> 8th-C55_S96 2 0.4755 0.6805 0.00 0.76 0.20 0.04
#> 8th-C57_S98 2 0.0000 0.8581 0.00 1.00 0.00 0.00
#> 8th-C58_S101 3 0.7885 0.4207 0.22 0.14 0.58 0.06
#> 8th-C67_S117 3 0.4778 0.6473 0.08 0.04 0.82 0.06
#> 8th-C74_S129 2 0.7121 0.2779 0.00 0.54 0.16 0.30
#> 8th-C85_S150 2 0.2411 0.8473 0.00 0.92 0.04 0.04
#> 9th-C57_S16 2 0.3037 0.8275 0.00 0.88 0.10 0.02
#> 9th-C80_S56 2 0.0707 0.8588 0.00 0.98 0.02 0.00
#> 9th-C83_S61 1 0.6299 0.4145 0.60 0.00 0.08 0.32
#> 9th-C9_S13 2 0.0000 0.8581 0.00 1.00 0.00 0.00
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
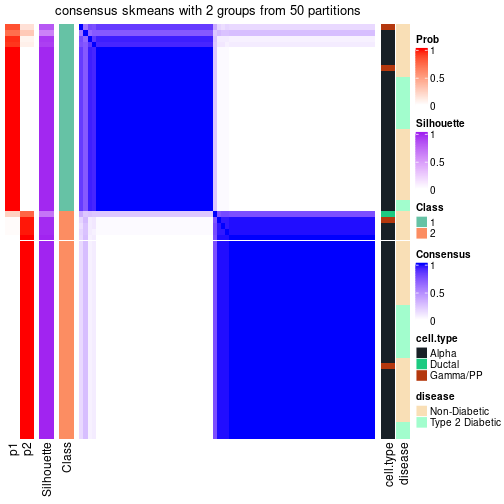
consensus_heatmap(res, k = 3)
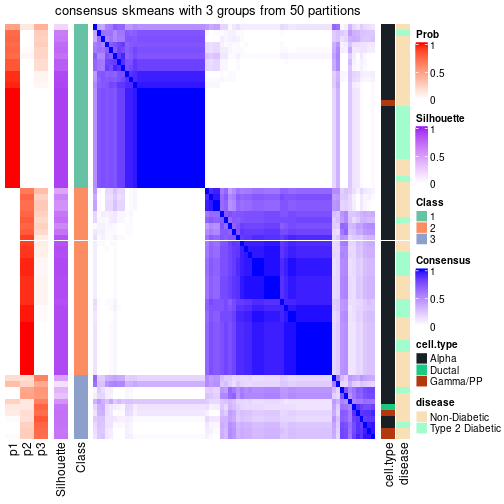
consensus_heatmap(res, k = 4)

Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
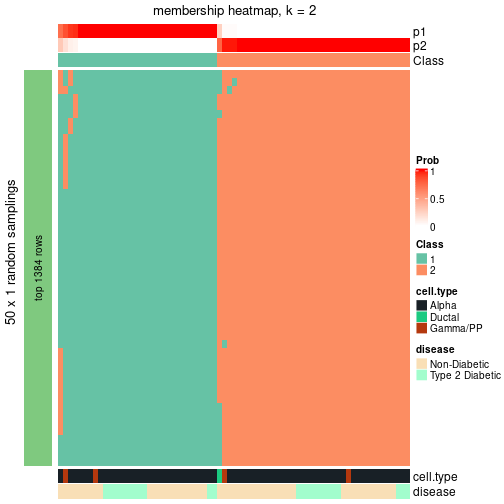
membership_heatmap(res, k = 3)
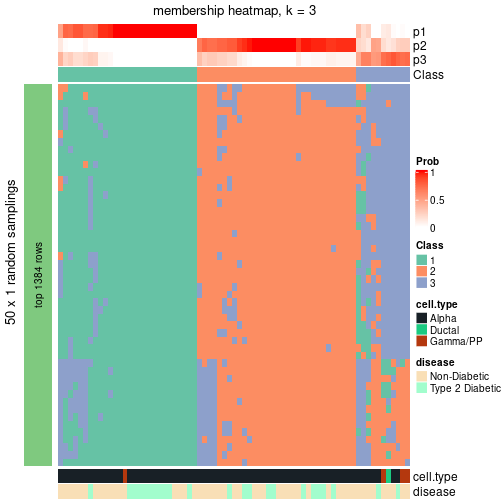
membership_heatmap(res, k = 4)

As soon as the classes for columns are determined, the signatures that are significantly different between subgroups can be looked for. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
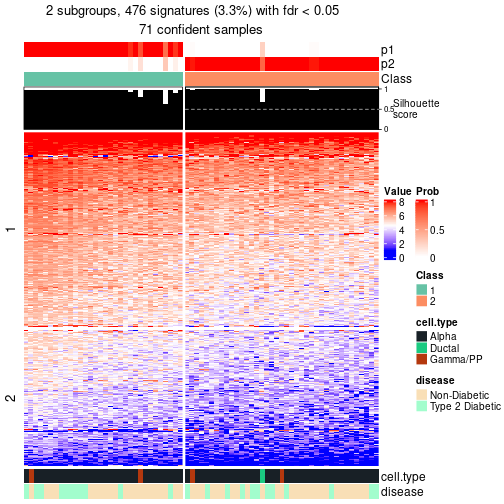
get_signatures(res, k = 3, scale_rows = FALSE)
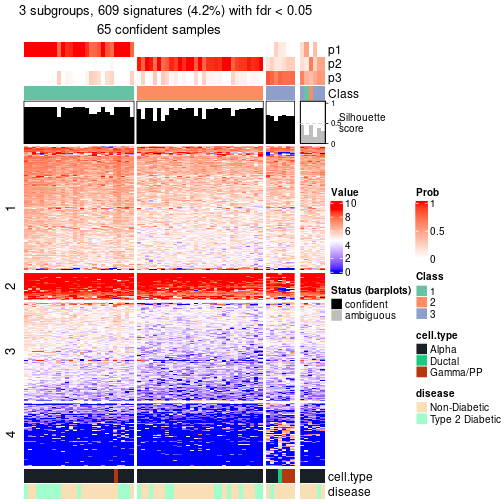
get_signatures(res, k = 4, scale_rows = FALSE)
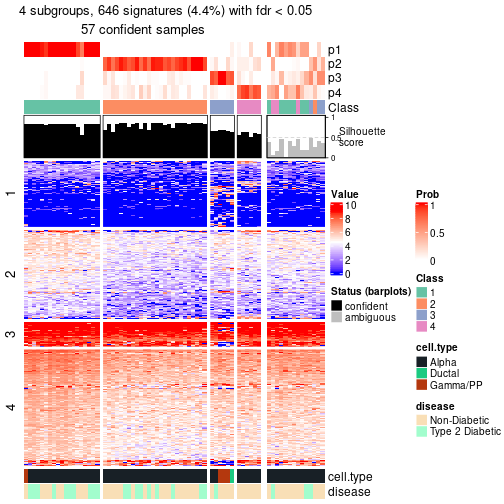
Compare the overlap of signatures from different k:
compare_signatures(res)
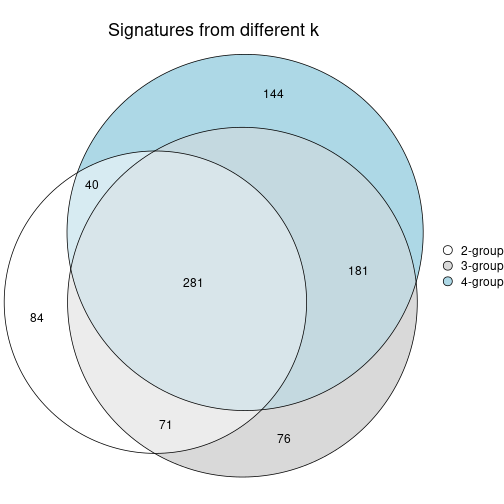
get_signature() returns a data frame invisibly. To get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows (which is done by automatically selecting number of clusters).If there are too many signatures, top_signatures = ... can be set to only show the
signatures with the highest FDRs:
# code only for demonstration
# e.g. to show the top 500 most significant rows
tb = get_signature(res, k = ..., top_signatures = 500)
If the signatures are defined as these which are uniquely high in current group, diff_method argument
can be set to "uniquely_high_in_one_group":
# code only for demonstration
tb = get_signature(res, k = ..., diff_method = "uniquely_high_in_one_group")
UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
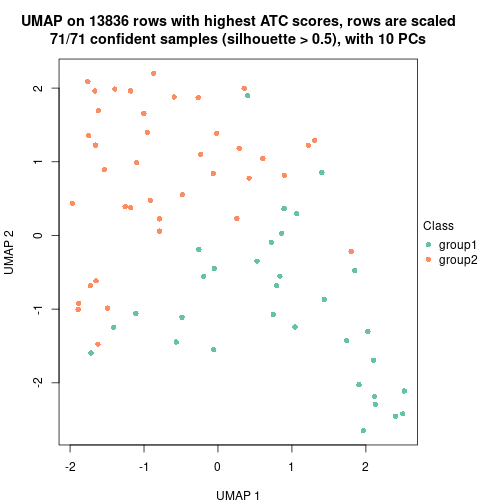
dimension_reduction(res, k = 3, method = "UMAP")
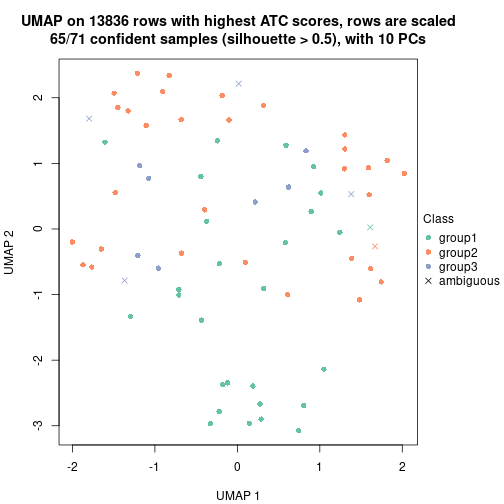
dimension_reduction(res, k = 4, method = "UMAP")
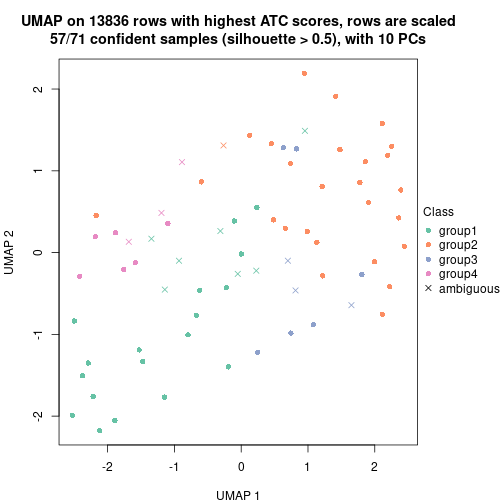
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
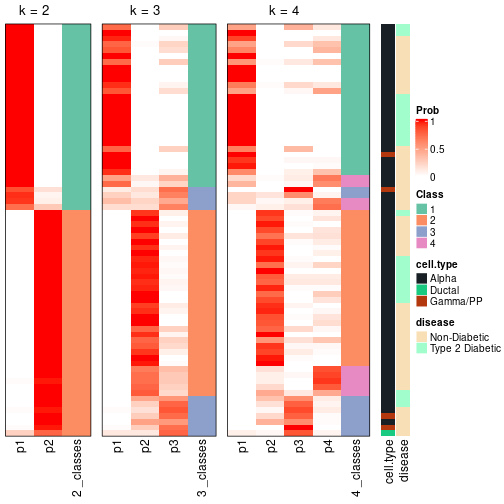
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n_sample cell.type(p-value) disease(p-value) k
#> ATC:skmeans 71 6.49e-01 0.9456 2
#> ATC:skmeans 65 1.32e-05 0.4057 3
#> ATC:skmeans 57 5.76e-05 0.0818 4
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
Parent node: Node011. Child nodes: Node01111-leaf , Node01112-leaf , Node01121-leaf , Node01122-leaf , Node01131-leaf , Node01132 , Node01221-leaf , Node01222-leaf , Node01223-leaf , Node01231-leaf , Node01232-leaf .
The object with results only for a single top-value method and a single partitioning method can be extracted as:
res = res_rh["0113"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4.
#> On a matrix with 13819 rows and 63 columns.
#> Top rows (1269) are extracted by 'ATC' method.
#> Subgroups are detected by 'skmeans' method.
#> Performed in total 150 partitions by row resampling.
#> Best k for subgroups seems to be 2.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_partitions"
#> [7] "compare_signatures" "consensus_heatmap" "dimension_reduction"
#> [10] "functional_enrichment" "get_anno_col" "get_anno"
#> [13] "get_classes" "get_consensus" "get_matrix"
#> [16] "get_membership" "get_param" "get_signatures"
#> [19] "get_stats" "is_best_k" "is_stable_k"
#> [22] "membership_heatmap" "ncol" "nrow"
#> [25] "plot_ecdf" "predict_classes" "rownames"
#> [28] "select_partition_number" "show" "suggest_best_k"
#> [31] "test_to_known_factors" "top_rows_heatmap"
collect_plots() function collects all the plots made from res for all k (number of subgroups)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
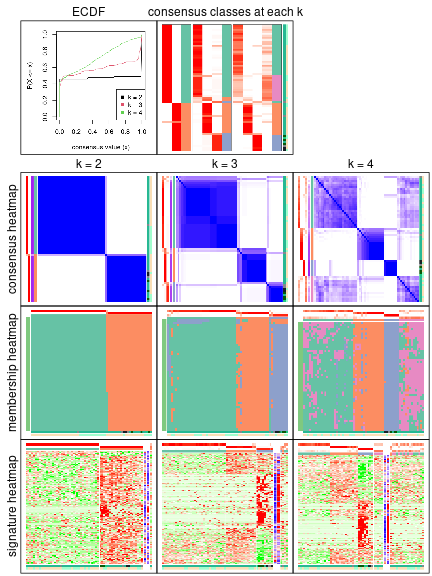
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, higher 1-PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
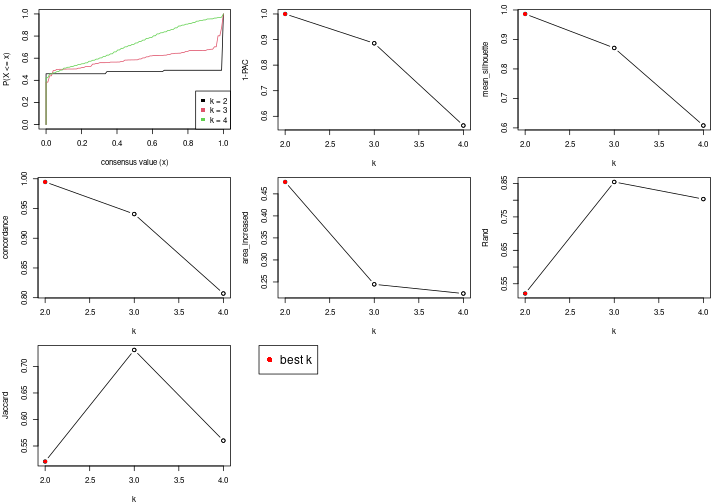
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 1.000 0.986 0.995 0.477 0.521 0.521
#> 3 3 0.885 0.871 0.941 0.245 0.855 0.731
#> 4 4 0.564 0.608 0.807 0.224 0.803 0.560
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 2
Following is the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall subgroup
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> 10th_C19_S62 2 0.000 0.985 0.00 1.00
#> 10th_C81_S70 1 0.000 1.000 1.00 0.00
#> 10th_C84_S115 1 0.000 1.000 1.00 0.00
#> 11th-C41_S60 2 0.000 0.985 0.00 1.00
#> 11th-C44_S15 1 0.000 1.000 1.00 0.00
#> 11th-C49_S23 1 0.000 1.000 1.00 0.00
#> 11th-C51_S39 1 0.000 1.000 1.00 0.00
#> 11th-C53_S78 1 0.000 1.000 1.00 0.00
#> 11th-C7_S16 2 0.000 0.985 0.00 1.00
#> 12th-C14_S190 1 0.000 1.000 1.00 0.00
#> 12th-C24_S141 1 0.000 1.000 1.00 0.00
#> 12th-C42_S159 1 0.000 1.000 1.00 0.00
#> 12th-C55_S203 2 0.000 0.985 0.00 1.00
#> 12th-C65_S170 1 0.000 1.000 1.00 0.00
#> 12th-C7_S196 1 0.000 1.000 1.00 0.00
#> 12th-C90_S166 1 0.000 1.000 1.00 0.00
#> 13th_C34_S181 1 0.000 1.000 1.00 0.00
#> 1st-C32_S14 2 0.000 0.985 0.00 1.00
#> 1st-C42_S71 2 0.000 0.985 0.00 1.00
#> 1st-C77_S86 2 0.000 0.985 0.00 1.00
#> 2nd-C21_S37 2 0.000 0.985 0.00 1.00
#> 2nd-C86_S77 2 0.000 0.985 0.00 1.00
#> 2nd-C95_S95 2 0.000 0.985 0.00 1.00
#> 3rd-C35_S23 2 0.000 0.985 0.00 1.00
#> 3rd-C65_S20 2 0.000 0.985 0.00 1.00
#> 3rd-C6_S44 2 0.000 0.985 0.00 1.00
#> 3rd-C9_S5 2 0.000 0.985 0.00 1.00
#> 4th-C36_S69 2 0.000 0.985 0.00 1.00
#> 4th-C67_S40 1 0.000 1.000 1.00 0.00
#> 5th-C35_S109 1 0.000 1.000 1.00 0.00
#> 5th-C90_S115 1 0.000 1.000 1.00 0.00
#> 6th-C20_S34 1 0.000 1.000 1.00 0.00
#> 6th-C22_S39 1 0.000 1.000 1.00 0.00
#> 6th-C24_S37 2 0.000 0.985 0.00 1.00
#> 6th-C2_S2 2 0.000 0.985 0.00 1.00
#> 6th-C30_S51 2 0.000 0.985 0.00 1.00
#> 6th-C40_S73 1 0.000 1.000 1.00 0.00
#> 6th-C42_S75 1 0.000 1.000 1.00 0.00
#> 6th-C51_S6 2 0.925 0.485 0.34 0.66
#> 6th-C66_S32 1 0.000 1.000 1.00 0.00
#> 6th-C73_S48 2 0.000 0.985 0.00 1.00
#> 6th-C75_S46 2 0.000 0.985 0.00 1.00
#> 6th-C80_S59 1 0.000 1.000 1.00 0.00
#> 7th-C10_S19 2 0.000 0.985 0.00 1.00
#> 7th-C31_S53 1 0.000 1.000 1.00 0.00
#> 7th-C50_S5 1 0.000 1.000 1.00 0.00
#> 7th-C66_S33 1 0.000 1.000 1.00 0.00
#> 7th-C73_S47 2 0.000 0.985 0.00 1.00
#> 7th-C80_S57 2 0.000 0.985 0.00 1.00
#> 7th-C89_S74 1 0.000 1.000 1.00 0.00
#> 8th-C44_S155 1 0.000 1.000 1.00 0.00
#> 9th-C10_S18 1 0.000 1.000 1.00 0.00
#> 9th-C11_S17 1 0.000 1.000 1.00 0.00
#> 9th-C1_S3 1 0.000 1.000 1.00 0.00
#> 9th-C38_S64 1 0.000 1.000 1.00 0.00
#> 9th-C3_S1 1 0.000 1.000 1.00 0.00
#> 9th-C46_S79 1 0.000 1.000 1.00 0.00
#> 9th-C6_S7 1 0.000 1.000 1.00 0.00
#> 9th-C81_S55 1 0.000 1.000 1.00 0.00
#> 9th-C86_S67 1 0.000 1.000 1.00 0.00
#> 9th-C89_S72 1 0.000 1.000 1.00 0.00
#> 9th-C8_S14 1 0.000 1.000 1.00 0.00
#> 9th-C93_S76 1 0.000 1.000 1.00 0.00
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> 10th_C19_S62 3 0.1529 0.905 0.00 0.04 0.96
#> 10th_C81_S70 1 0.0000 0.947 1.00 0.00 0.00
#> 10th_C84_S115 1 0.0000 0.947 1.00 0.00 0.00
#> 11th-C41_S60 2 0.0000 0.925 0.00 1.00 0.00
#> 11th-C44_S15 1 0.0892 0.947 0.98 0.00 0.02
#> 11th-C49_S23 1 0.6244 0.153 0.56 0.44 0.00
#> 11th-C51_S39 1 0.0000 0.947 1.00 0.00 0.00
#> 11th-C53_S78 1 0.0000 0.947 1.00 0.00 0.00
#> 11th-C7_S16 3 0.1529 0.905 0.00 0.04 0.96
#> 12th-C14_S190 1 0.1529 0.945 0.96 0.00 0.04
#> 12th-C24_S141 1 0.1529 0.945 0.96 0.00 0.04
#> 12th-C42_S159 1 0.0000 0.947 1.00 0.00 0.00
#> 12th-C55_S203 2 0.0000 0.925 0.00 1.00 0.00
#> 12th-C65_S170 1 0.1781 0.936 0.96 0.02 0.02
#> 12th-C7_S196 1 0.1529 0.945 0.96 0.00 0.04
#> 12th-C90_S166 1 0.1529 0.945 0.96 0.00 0.04
#> 13th_C34_S181 2 0.6633 0.543 0.26 0.70 0.04
#> 1st-C32_S14 2 0.0000 0.925 0.00 1.00 0.00
#> 1st-C42_S71 3 0.1529 0.905 0.00 0.04 0.96
#> 1st-C77_S86 3 0.6244 0.229 0.00 0.44 0.56
#> 2nd-C21_S37 3 0.1529 0.905 0.00 0.04 0.96
#> 2nd-C86_S77 2 0.0000 0.925 0.00 1.00 0.00
#> 2nd-C95_S95 2 0.0000 0.925 0.00 1.00 0.00
#> 3rd-C35_S23 3 0.1529 0.905 0.00 0.04 0.96
#> 3rd-C65_S20 2 0.0892 0.912 0.02 0.98 0.00
#> 3rd-C6_S44 3 0.1781 0.887 0.02 0.02 0.96
#> 3rd-C9_S5 3 0.1529 0.905 0.00 0.04 0.96
#> 4th-C36_S69 3 0.1529 0.905 0.00 0.04 0.96
#> 4th-C67_S40 1 0.0000 0.947 1.00 0.00 0.00
#> 5th-C35_S109 3 0.5216 0.597 0.26 0.00 0.74
#> 5th-C90_S115 1 0.6192 0.243 0.58 0.00 0.42
#> 6th-C20_S34 1 0.1529 0.945 0.96 0.00 0.04
#> 6th-C22_S39 1 0.1529 0.945 0.96 0.00 0.04
#> 6th-C24_S37 2 0.5706 0.454 0.00 0.68 0.32
#> 6th-C2_S2 2 0.0000 0.925 0.00 1.00 0.00
#> 6th-C30_S51 2 0.0892 0.912 0.02 0.98 0.00
#> 6th-C40_S73 1 0.1529 0.945 0.96 0.00 0.04
#> 6th-C42_S75 1 0.0892 0.947 0.98 0.00 0.02
#> 6th-C51_S6 2 0.0892 0.912 0.02 0.98 0.00
#> 6th-C66_S32 1 0.1529 0.945 0.96 0.00 0.04
#> 6th-C73_S48 2 0.0000 0.925 0.00 1.00 0.00
#> 6th-C75_S46 2 0.0000 0.925 0.00 1.00 0.00
#> 6th-C80_S59 1 0.1529 0.945 0.96 0.00 0.04
#> 7th-C10_S19 2 0.0000 0.925 0.00 1.00 0.00
#> 7th-C31_S53 2 0.5746 0.666 0.18 0.78 0.04
#> 7th-C50_S5 1 0.2414 0.919 0.94 0.04 0.02
#> 7th-C66_S33 1 0.1529 0.945 0.96 0.00 0.04
#> 7th-C73_S47 2 0.0000 0.925 0.00 1.00 0.00
#> 7th-C80_S57 2 0.0000 0.925 0.00 1.00 0.00
#> 7th-C89_S74 1 0.0000 0.947 1.00 0.00 0.00
#> 8th-C44_S155 1 0.0000 0.947 1.00 0.00 0.00
#> 9th-C10_S18 1 0.3572 0.898 0.90 0.06 0.04
#> 9th-C11_S17 1 0.0000 0.947 1.00 0.00 0.00
#> 9th-C1_S3 1 0.0892 0.947 0.98 0.00 0.02
#> 9th-C38_S64 1 0.1529 0.945 0.96 0.00 0.04
#> 9th-C3_S1 1 0.0000 0.947 1.00 0.00 0.00
#> 9th-C46_S79 1 0.0000 0.947 1.00 0.00 0.00
#> 9th-C6_S7 1 0.0000 0.947 1.00 0.00 0.00
#> 9th-C81_S55 1 0.0000 0.947 1.00 0.00 0.00
#> 9th-C86_S67 1 0.0892 0.947 0.98 0.00 0.02
#> 9th-C89_S72 1 0.1529 0.945 0.96 0.00 0.04
#> 9th-C8_S14 1 0.0000 0.947 1.00 0.00 0.00
#> 9th-C93_S76 1 0.4555 0.725 0.80 0.00 0.20
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> 10th_C19_S62 3 0.0000 0.9967 0.00 0.00 1.00 0.00
#> 10th_C81_S70 1 0.2345 0.6283 0.90 0.00 0.00 0.10
#> 10th_C84_S115 1 0.3172 0.6149 0.84 0.00 0.00 0.16
#> 11th-C41_S60 2 0.6731 0.5253 0.02 0.62 0.08 0.28
#> 11th-C44_S15 1 0.4713 0.3872 0.64 0.00 0.00 0.36
#> 11th-C49_S23 4 0.6805 0.0849 0.40 0.10 0.00 0.50
#> 11th-C51_S39 1 0.3610 0.6053 0.80 0.00 0.00 0.20
#> 11th-C53_S78 1 0.1211 0.6518 0.96 0.00 0.00 0.04
#> 11th-C7_S16 3 0.0000 0.9967 0.00 0.00 1.00 0.00
#> 12th-C14_S190 1 0.3801 0.5501 0.78 0.00 0.00 0.22
#> 12th-C24_S141 1 0.4624 0.3513 0.66 0.00 0.00 0.34
#> 12th-C42_S159 1 0.2011 0.6448 0.92 0.00 0.00 0.08
#> 12th-C55_S203 2 0.1637 0.8736 0.00 0.94 0.00 0.06
#> 12th-C65_S170 4 0.4936 0.5094 0.28 0.02 0.00 0.70
#> 12th-C7_S196 1 0.4522 0.4391 0.68 0.00 0.00 0.32
#> 12th-C90_S166 4 0.4994 0.0719 0.48 0.00 0.00 0.52
#> 13th_C34_S181 4 0.5291 0.4467 0.08 0.18 0.00 0.74
#> 1st-C32_S14 2 0.0000 0.9050 0.00 1.00 0.00 0.00
#> 1st-C42_S71 3 0.0000 0.9967 0.00 0.00 1.00 0.00
#> 1st-C77_S86 2 0.4855 0.3729 0.00 0.60 0.40 0.00
#> 2nd-C21_S37 3 0.0000 0.9967 0.00 0.00 1.00 0.00
#> 2nd-C86_S77 2 0.0000 0.9050 0.00 1.00 0.00 0.00
#> 2nd-C95_S95 2 0.0000 0.9050 0.00 1.00 0.00 0.00
#> 3rd-C35_S23 3 0.0000 0.9967 0.00 0.00 1.00 0.00
#> 3rd-C65_S20 2 0.2345 0.8485 0.00 0.90 0.00 0.10
#> 3rd-C6_S44 3 0.0000 0.9967 0.00 0.00 1.00 0.00
#> 3rd-C9_S5 3 0.0707 0.9768 0.00 0.02 0.98 0.00
#> 4th-C36_S69 3 0.0000 0.9967 0.00 0.00 1.00 0.00
#> 4th-C67_S40 1 0.4624 0.3273 0.66 0.00 0.00 0.34
#> 5th-C35_S109 1 0.7365 0.0765 0.44 0.00 0.40 0.16
#> 5th-C90_S115 1 0.5820 0.4103 0.68 0.00 0.24 0.08
#> 6th-C20_S34 4 0.4522 0.5156 0.32 0.00 0.00 0.68
#> 6th-C22_S39 4 0.4406 0.5099 0.30 0.00 0.00 0.70
#> 6th-C24_S37 2 0.3172 0.7808 0.00 0.84 0.16 0.00
#> 6th-C2_S2 2 0.0000 0.9050 0.00 1.00 0.00 0.00
#> 6th-C30_S51 2 0.1211 0.8870 0.00 0.96 0.00 0.04
#> 6th-C40_S73 1 0.4624 0.2431 0.66 0.00 0.00 0.34
#> 6th-C42_S75 1 0.3400 0.5923 0.82 0.00 0.00 0.18
#> 6th-C51_S6 2 0.4134 0.6654 0.00 0.74 0.00 0.26
#> 6th-C66_S32 4 0.4406 0.5121 0.30 0.00 0.00 0.70
#> 6th-C73_S48 2 0.0000 0.9050 0.00 1.00 0.00 0.00
#> 6th-C75_S46 2 0.0000 0.9050 0.00 1.00 0.00 0.00
#> 6th-C80_S59 4 0.4522 0.5168 0.32 0.00 0.00 0.68
#> 7th-C10_S19 2 0.0000 0.9050 0.00 1.00 0.00 0.00
#> 7th-C31_S53 4 0.5986 0.3028 0.06 0.32 0.00 0.62
#> 7th-C50_S5 4 0.6150 0.3902 0.36 0.06 0.00 0.58
#> 7th-C66_S33 4 0.4977 0.3614 0.46 0.00 0.00 0.54
#> 7th-C73_S47 2 0.0000 0.9050 0.00 1.00 0.00 0.00
#> 7th-C80_S57 2 0.0000 0.9050 0.00 1.00 0.00 0.00
#> 7th-C89_S74 4 0.4790 0.4060 0.38 0.00 0.00 0.62
#> 8th-C44_S155 1 0.4994 0.0188 0.52 0.00 0.00 0.48
#> 9th-C10_S18 4 0.5355 0.2959 0.36 0.02 0.00 0.62
#> 9th-C11_S17 1 0.4406 0.5019 0.70 0.00 0.00 0.30
#> 9th-C1_S3 1 0.1637 0.6424 0.94 0.00 0.00 0.06
#> 9th-C38_S64 1 0.1637 0.6482 0.94 0.00 0.00 0.06
#> 9th-C3_S1 1 0.1637 0.6479 0.94 0.00 0.00 0.06
#> 9th-C46_S79 1 0.3801 0.5204 0.78 0.00 0.00 0.22
#> 9th-C6_S7 1 0.2345 0.6232 0.90 0.00 0.00 0.10
#> 9th-C81_S55 1 0.4977 -0.1593 0.54 0.00 0.00 0.46
#> 9th-C86_S67 1 0.2921 0.6096 0.86 0.00 0.00 0.14
#> 9th-C89_S72 1 0.3610 0.5977 0.80 0.00 0.00 0.20
#> 9th-C8_S14 1 0.2647 0.6251 0.88 0.00 0.00 0.12
#> 9th-C93_S76 1 0.5383 0.5336 0.74 0.00 0.10 0.16
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
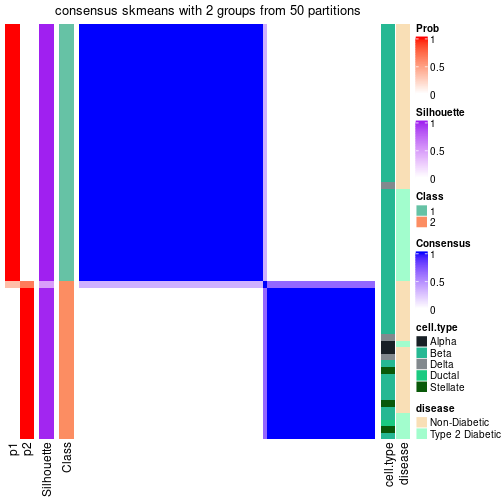
consensus_heatmap(res, k = 3)
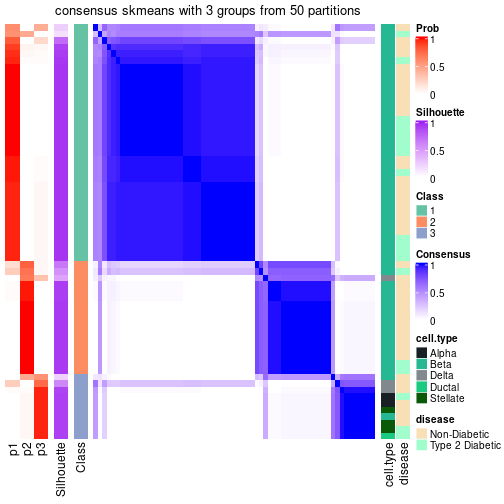
consensus_heatmap(res, k = 4)
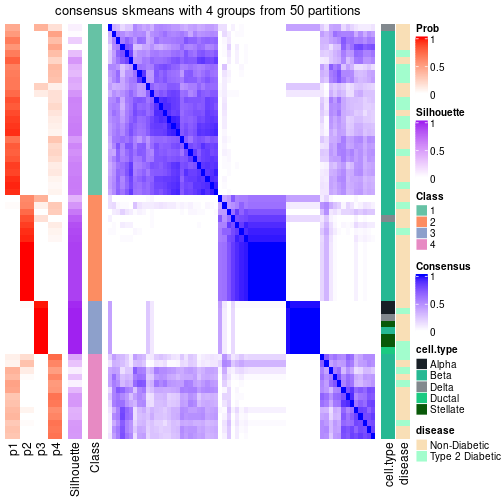
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
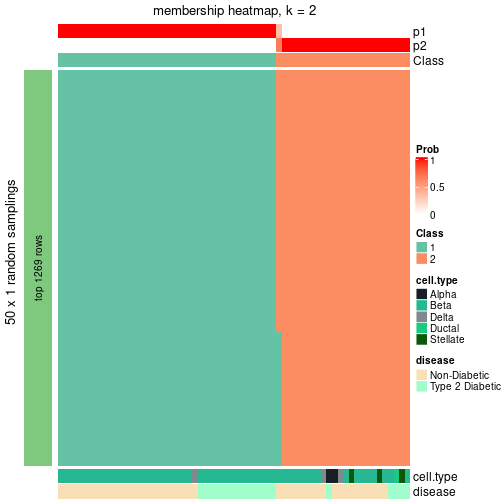
membership_heatmap(res, k = 3)
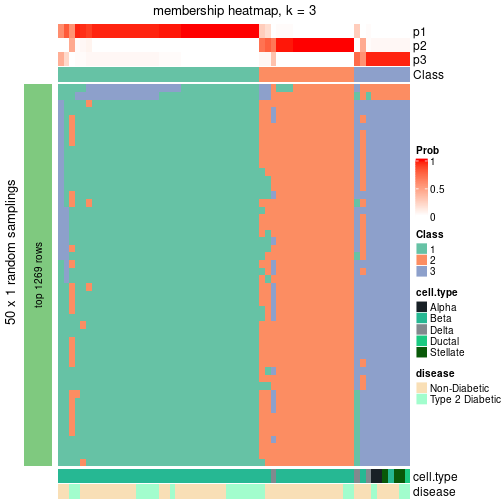
membership_heatmap(res, k = 4)
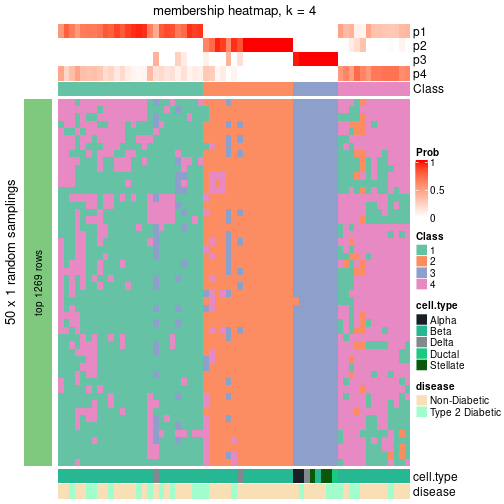
As soon as the classes for columns are determined, the signatures that are significantly different between subgroups can be looked for. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
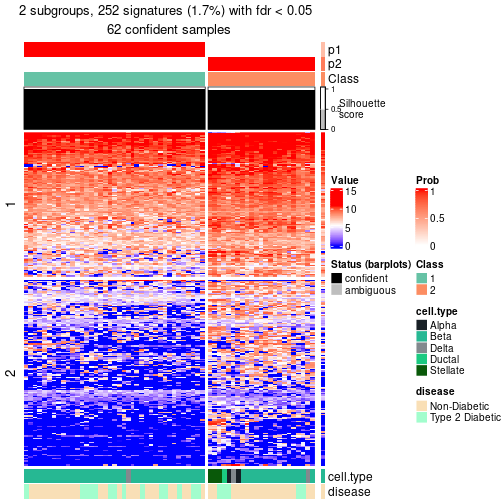
get_signatures(res, k = 3, scale_rows = FALSE)
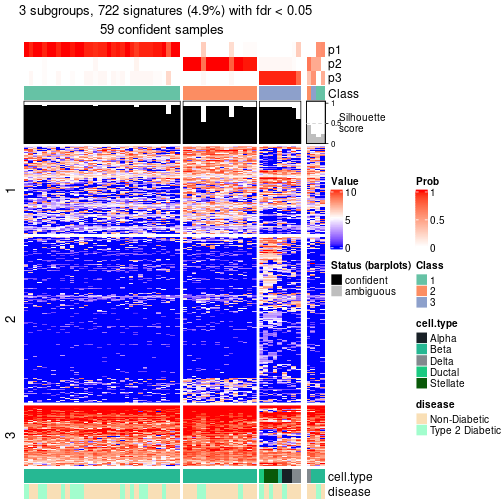
get_signatures(res, k = 4, scale_rows = FALSE)
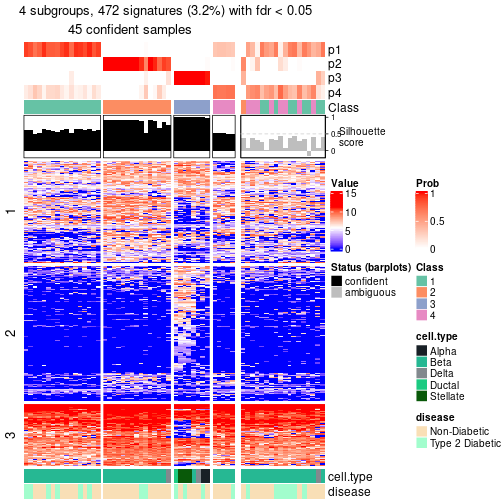
Compare the overlap of signatures from different k:
compare_signatures(res)
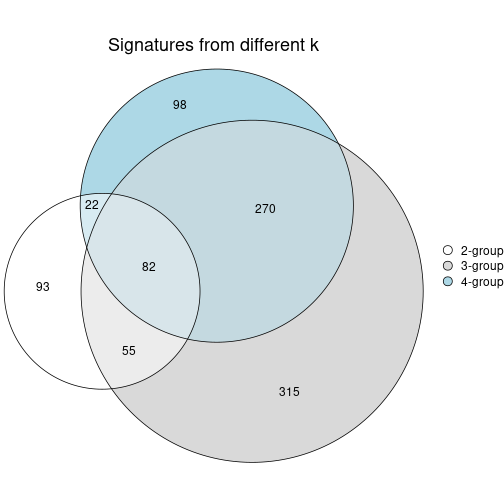
get_signature() returns a data frame invisibly. To get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows (which is done by automatically selecting number of clusters).If there are too many signatures, top_signatures = ... can be set to only show the
signatures with the highest FDRs:
# code only for demonstration
# e.g. to show the top 500 most significant rows
tb = get_signature(res, k = ..., top_signatures = 500)
If the signatures are defined as these which are uniquely high in current group, diff_method argument
can be set to "uniquely_high_in_one_group":
# code only for demonstration
tb = get_signature(res, k = ..., diff_method = "uniquely_high_in_one_group")
UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
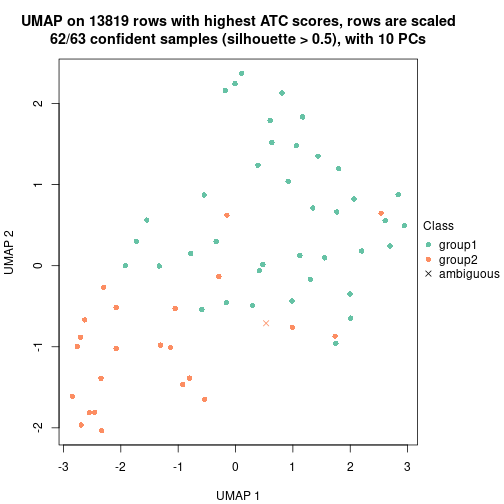
dimension_reduction(res, k = 3, method = "UMAP")
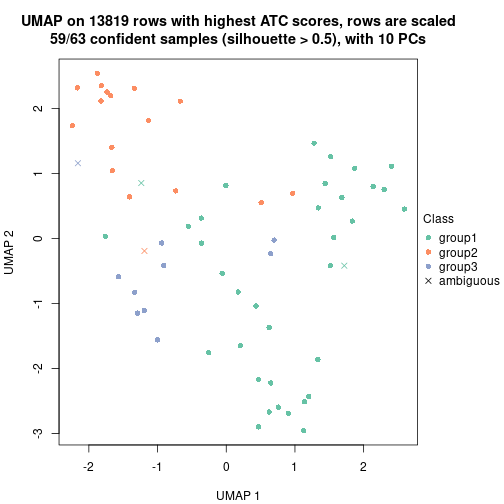
dimension_reduction(res, k = 4, method = "UMAP")
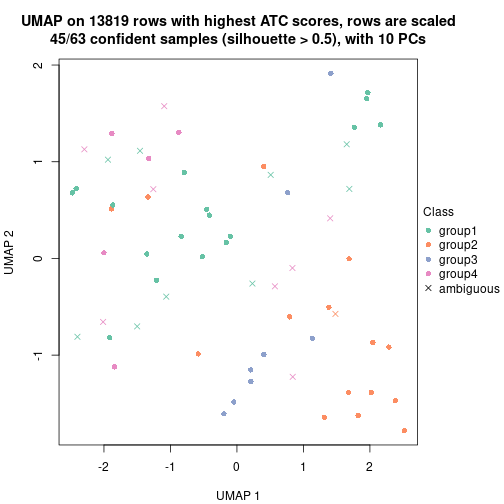
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
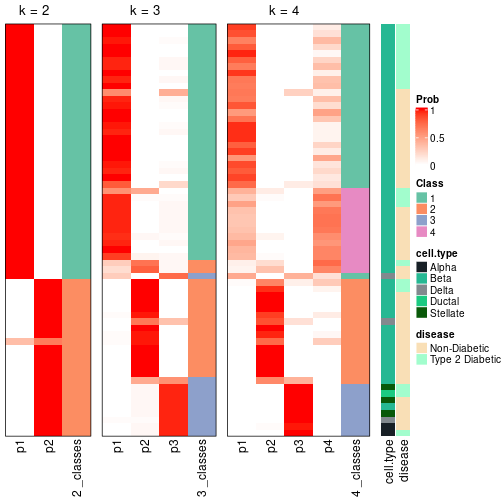
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n_sample cell.type(p-value) disease(p-value) k
#> ATC:skmeans 62 1.10e-02 0.377 2
#> ATC:skmeans 59 2.18e-08 0.486 3
#> ATC:skmeans 45 3.41e-04 0.457 4
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
Parent node: Node0113. Child nodes: Node011321-leaf , Node011322-leaf .
The object with results only for a single top-value method and a single partitioning method can be extracted as:
res = res_rh["01132"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4.
#> On a matrix with 13633 rows and 24 columns.
#> Top rows (1363) are extracted by 'ATC' method.
#> Subgroups are detected by 'skmeans' method.
#> Performed in total 150 partitions by row resampling.
#> Best k for subgroups seems to be 2.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_partitions"
#> [7] "compare_signatures" "consensus_heatmap" "dimension_reduction"
#> [10] "functional_enrichment" "get_anno_col" "get_anno"
#> [13] "get_classes" "get_consensus" "get_matrix"
#> [16] "get_membership" "get_param" "get_signatures"
#> [19] "get_stats" "is_best_k" "is_stable_k"
#> [22] "membership_heatmap" "ncol" "nrow"
#> [25] "plot_ecdf" "predict_classes" "rownames"
#> [28] "select_partition_number" "show" "suggest_best_k"
#> [31] "test_to_known_factors" "top_rows_heatmap"
collect_plots() function collects all the plots made from res for all k (number of subgroups)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
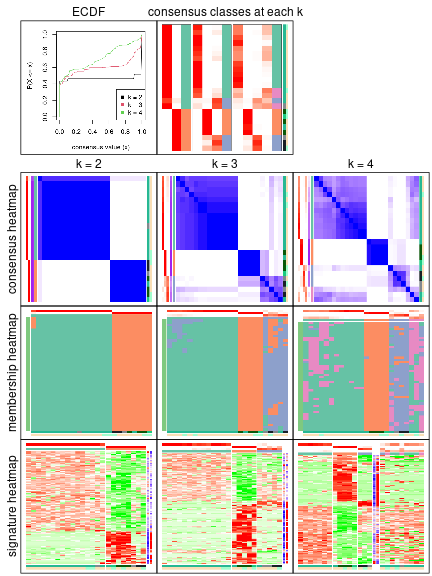
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, higher 1-PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
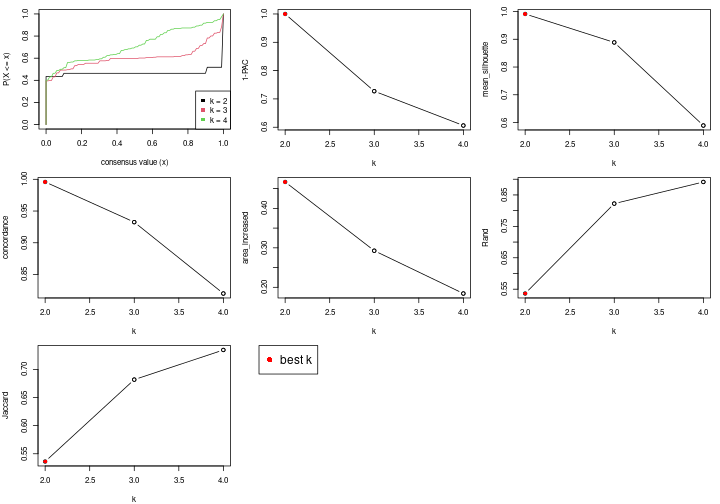
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 1.000 0.991 0.996 0.467 0.536 0.536
#> 3 3 0.727 0.889 0.932 0.293 0.822 0.682
#> 4 4 0.606 0.589 0.820 0.184 0.891 0.735
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 2
Following is the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall subgroup
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> 10th_C19_S62 2 0.000 1.000 0.0 1.0
#> 11th-C41_S60 1 0.000 0.993 1.0 0.0
#> 11th-C7_S16 2 0.000 1.000 0.0 1.0
#> 12th-C55_S203 1 0.000 0.993 1.0 0.0
#> 1st-C32_S14 1 0.000 0.993 1.0 0.0
#> 1st-C42_S71 2 0.000 1.000 0.0 1.0
#> 1st-C77_S86 1 0.469 0.889 0.9 0.1
#> 2nd-C21_S37 2 0.000 1.000 0.0 1.0
#> 2nd-C86_S77 1 0.000 0.993 1.0 0.0
#> 2nd-C95_S95 1 0.000 0.993 1.0 0.0
#> 3rd-C35_S23 2 0.000 1.000 0.0 1.0
#> 3rd-C65_S20 1 0.000 0.993 1.0 0.0
#> 3rd-C6_S44 2 0.000 1.000 0.0 1.0
#> 3rd-C9_S5 2 0.000 1.000 0.0 1.0
#> 4th-C36_S69 2 0.000 1.000 0.0 1.0
#> 6th-C24_S37 1 0.000 0.993 1.0 0.0
#> 6th-C2_S2 1 0.000 0.993 1.0 0.0
#> 6th-C30_S51 1 0.000 0.993 1.0 0.0
#> 6th-C51_S6 1 0.000 0.993 1.0 0.0
#> 6th-C73_S48 1 0.000 0.993 1.0 0.0
#> 6th-C75_S46 1 0.000 0.993 1.0 0.0
#> 7th-C10_S19 1 0.000 0.993 1.0 0.0
#> 7th-C73_S47 1 0.000 0.993 1.0 0.0
#> 7th-C80_S57 1 0.000 0.993 1.0 0.0
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> 10th_C19_S62 2 0.0000 1.000 0.00 1.00 0.00
#> 11th-C41_S60 1 0.2959 0.910 0.90 0.00 0.10
#> 11th-C7_S16 2 0.0000 1.000 0.00 1.00 0.00
#> 12th-C55_S203 1 0.0892 0.951 0.98 0.00 0.02
#> 1st-C32_S14 1 0.2959 0.896 0.90 0.00 0.10
#> 1st-C42_S71 2 0.0000 1.000 0.00 1.00 0.00
#> 1st-C77_S86 3 0.3572 0.727 0.06 0.04 0.90
#> 2nd-C21_S37 2 0.0000 1.000 0.00 1.00 0.00
#> 2nd-C86_S77 1 0.0000 0.956 1.00 0.00 0.00
#> 2nd-C95_S95 1 0.0000 0.956 1.00 0.00 0.00
#> 3rd-C35_S23 2 0.0000 1.000 0.00 1.00 0.00
#> 3rd-C65_S20 1 0.4291 0.831 0.82 0.00 0.18
#> 3rd-C6_S44 3 0.5560 0.626 0.00 0.30 0.70
#> 3rd-C9_S5 3 0.2537 0.738 0.00 0.08 0.92
#> 4th-C36_S69 3 0.5948 0.544 0.00 0.36 0.64
#> 6th-C24_S37 3 0.4002 0.646 0.16 0.00 0.84
#> 6th-C2_S2 1 0.0892 0.951 0.98 0.00 0.02
#> 6th-C30_S51 1 0.2066 0.937 0.94 0.00 0.06
#> 6th-C51_S6 1 0.3686 0.880 0.86 0.00 0.14
#> 6th-C73_S48 1 0.0000 0.956 1.00 0.00 0.00
#> 6th-C75_S46 1 0.0000 0.956 1.00 0.00 0.00
#> 7th-C10_S19 1 0.0000 0.956 1.00 0.00 0.00
#> 7th-C73_S47 1 0.0000 0.956 1.00 0.00 0.00
#> 7th-C80_S57 1 0.0000 0.956 1.00 0.00 0.00
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> 10th_C19_S62 2 0.0000 0.9941 0.00 1.00 0.00 0.00
#> 11th-C41_S60 4 0.5173 0.1874 0.32 0.00 0.02 0.66
#> 11th-C7_S16 2 0.0000 0.9941 0.00 1.00 0.00 0.00
#> 12th-C55_S203 1 0.4624 0.4539 0.66 0.00 0.00 0.34
#> 1st-C32_S14 1 0.5173 0.3937 0.66 0.00 0.02 0.32
#> 1st-C42_S71 2 0.0000 0.9941 0.00 1.00 0.00 0.00
#> 1st-C77_S86 3 0.7347 0.3687 0.12 0.02 0.56 0.30
#> 2nd-C21_S37 2 0.0707 0.9763 0.00 0.98 0.02 0.00
#> 2nd-C86_S77 1 0.2921 0.6688 0.86 0.00 0.00 0.14
#> 2nd-C95_S95 1 0.0707 0.7170 0.98 0.00 0.00 0.02
#> 3rd-C35_S23 2 0.0000 0.9941 0.00 1.00 0.00 0.00
#> 3rd-C65_S20 4 0.5987 0.0299 0.44 0.00 0.04 0.52
#> 3rd-C6_S44 3 0.3821 0.7517 0.00 0.12 0.84 0.04
#> 3rd-C9_S5 3 0.1211 0.7607 0.00 0.04 0.96 0.00
#> 4th-C36_S69 3 0.3335 0.7641 0.00 0.12 0.86 0.02
#> 6th-C24_S37 4 0.6299 -0.1967 0.06 0.00 0.42 0.52
#> 6th-C2_S2 1 0.4713 0.4141 0.64 0.00 0.00 0.36
#> 6th-C30_S51 1 0.5487 0.1775 0.58 0.00 0.02 0.40
#> 6th-C51_S6 1 0.5487 0.1365 0.58 0.00 0.02 0.40
#> 6th-C73_S48 1 0.2345 0.6909 0.90 0.00 0.00 0.10
#> 6th-C75_S46 1 0.1211 0.7152 0.96 0.00 0.00 0.04
#> 7th-C10_S19 1 0.0707 0.7176 0.98 0.00 0.00 0.02
#> 7th-C73_S47 1 0.0000 0.7187 1.00 0.00 0.00 0.00
#> 7th-C80_S57 1 0.0707 0.7176 0.98 0.00 0.00 0.02
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
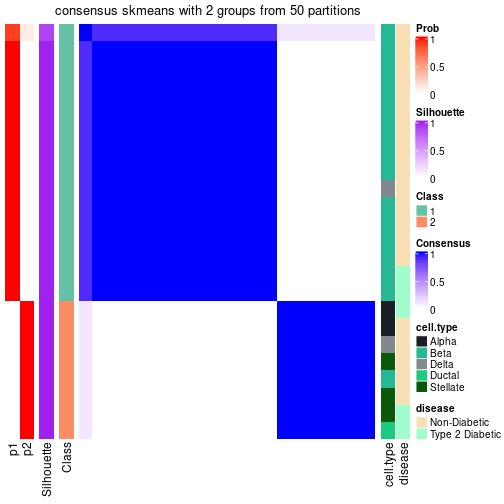
consensus_heatmap(res, k = 3)
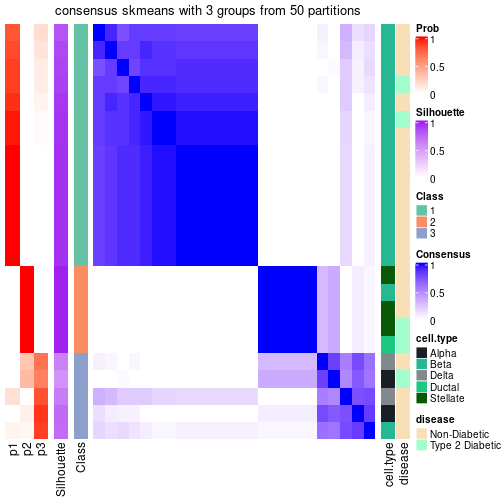
consensus_heatmap(res, k = 4)
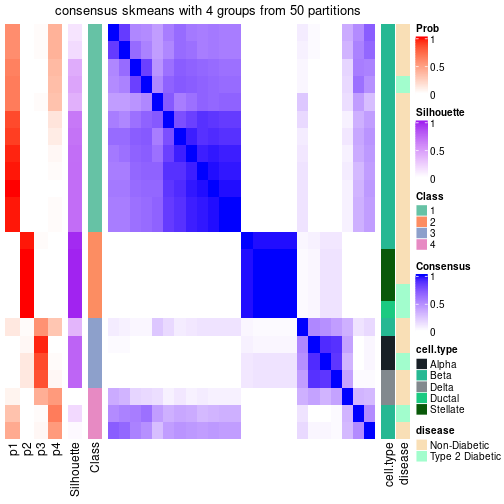
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
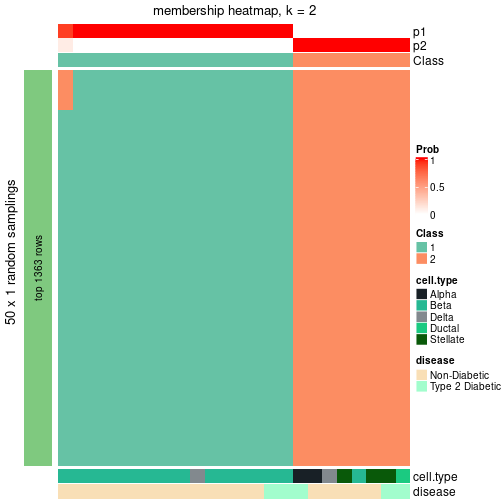
membership_heatmap(res, k = 3)
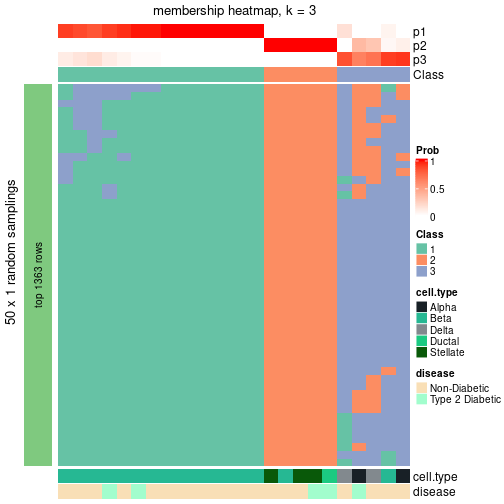
membership_heatmap(res, k = 4)

As soon as the classes for columns are determined, the signatures that are significantly different between subgroups can be looked for. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
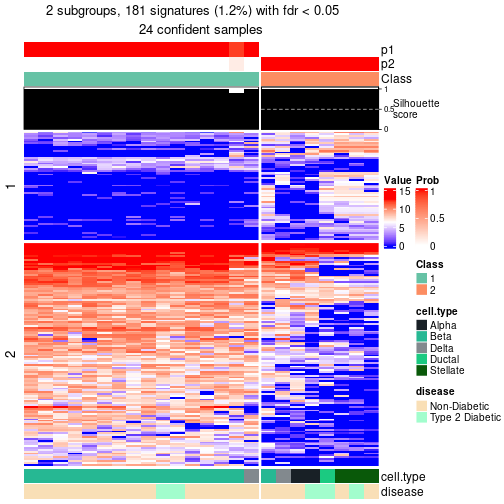
get_signatures(res, k = 3, scale_rows = FALSE)
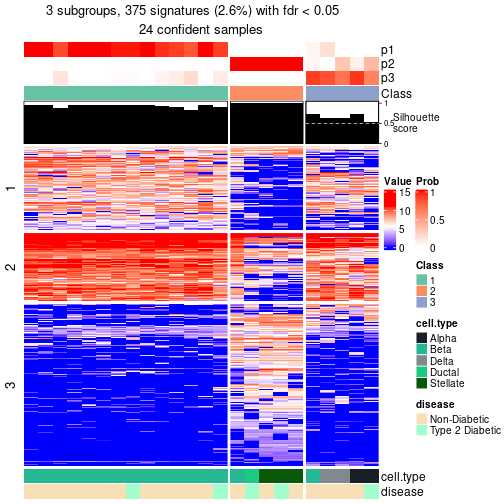
get_signatures(res, k = 4, scale_rows = FALSE)
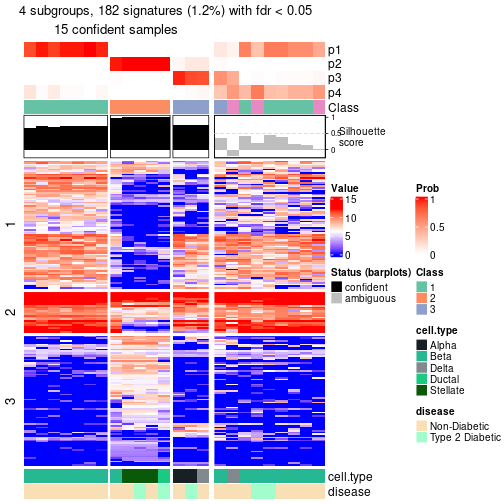
Compare the overlap of signatures from different k:
compare_signatures(res)
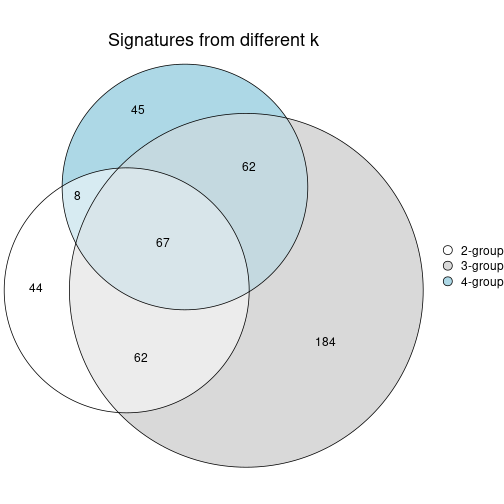
get_signature() returns a data frame invisibly. To get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows (which is done by automatically selecting number of clusters).If there are too many signatures, top_signatures = ... can be set to only show the
signatures with the highest FDRs:
# code only for demonstration
# e.g. to show the top 500 most significant rows
tb = get_signature(res, k = ..., top_signatures = 500)
If the signatures are defined as these which are uniquely high in current group, diff_method argument
can be set to "uniquely_high_in_one_group":
# code only for demonstration
tb = get_signature(res, k = ..., diff_method = "uniquely_high_in_one_group")
UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
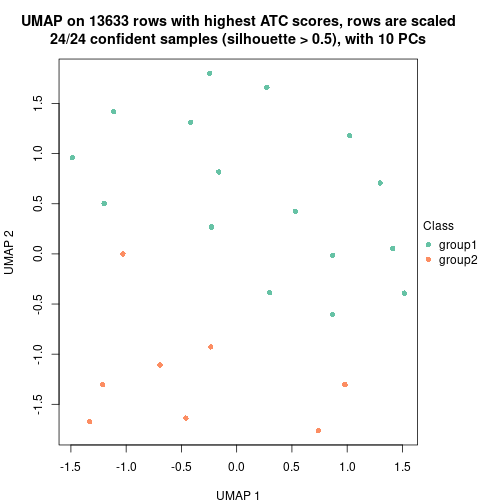
dimension_reduction(res, k = 3, method = "UMAP")
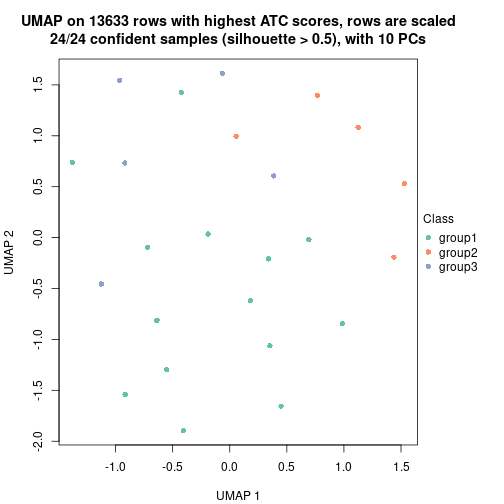
dimension_reduction(res, k = 4, method = "UMAP")

Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
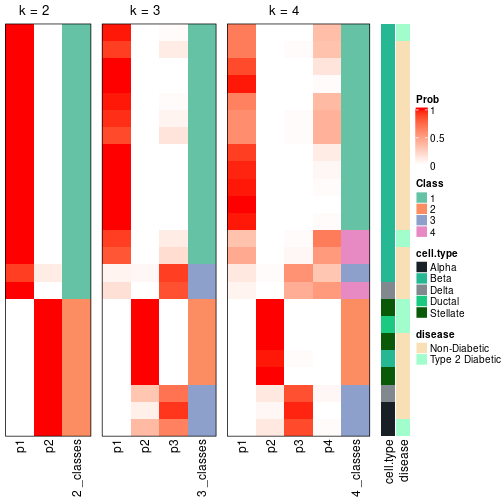
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n_sample cell.type(p-value) disease(p-value) k
#> ATC:skmeans 24 1.52e-03 0.374 2
#> ATC:skmeans 24 1.76e-05 0.477 3
#> ATC:skmeans 15 1.28e-03 0.189 4
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
Parent node: Node01. Child nodes: Node0111 , Node0112 , Node0113 , Node0121-leaf , Node0122 , Node0123 , Node0124-leaf , Node0211-leaf , Node0212-leaf , Node0221-leaf , Node0222-leaf , Node0231-leaf , Node0232-leaf , Node0233-leaf .
The object with results only for a single top-value method and a single partitioning method can be extracted as:
res = res_rh["012"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4.
#> On a matrix with 13871 rows and 170 columns.
#> Top rows (1387) are extracted by 'ATC' method.
#> Subgroups are detected by 'skmeans' method.
#> Performed in total 150 partitions by row resampling.
#> Best k for subgroups seems to be 4.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_partitions"
#> [7] "compare_signatures" "consensus_heatmap" "dimension_reduction"
#> [10] "functional_enrichment" "get_anno_col" "get_anno"
#> [13] "get_classes" "get_consensus" "get_matrix"
#> [16] "get_membership" "get_param" "get_signatures"
#> [19] "get_stats" "is_best_k" "is_stable_k"
#> [22] "membership_heatmap" "ncol" "nrow"
#> [25] "plot_ecdf" "predict_classes" "rownames"
#> [28] "select_partition_number" "show" "suggest_best_k"
#> [31] "test_to_known_factors" "top_rows_heatmap"
collect_plots() function collects all the plots made from res for all k (number of subgroups)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
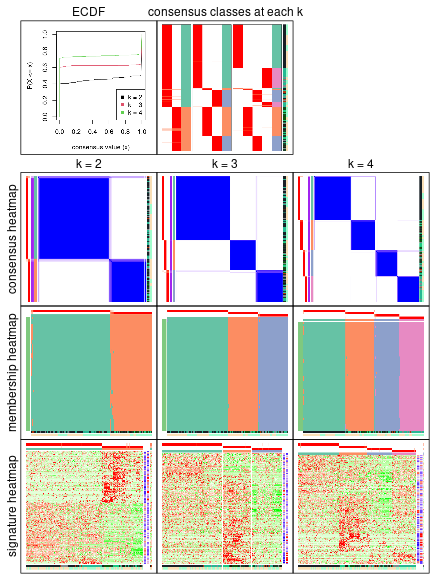
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, higher 1-PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
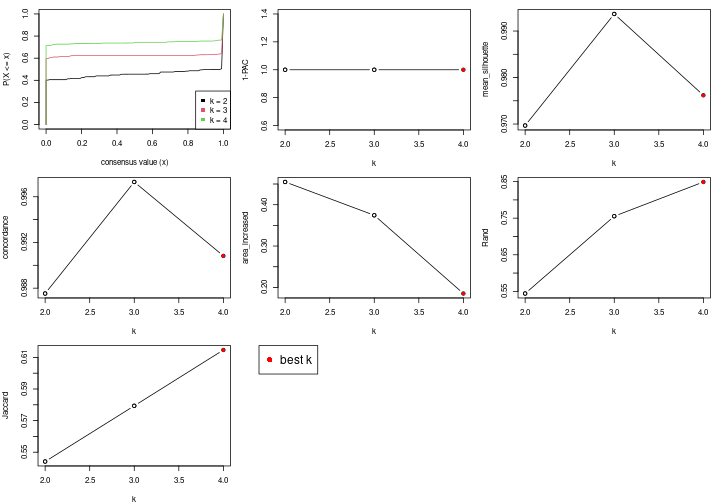
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 1 0.970 0.988 0.455 0.544 0.544
#> 3 3 1 0.994 0.997 0.374 0.755 0.579
#> 4 4 1 0.976 0.991 0.185 0.849 0.615
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 4
#> attr(,"optional")
#> [1] 2 3
There is also optional best \(k\) = 2 3 that is worth to check.
Following is the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall subgroup
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> 10th_C10_S104 2 0.000 0.978 0.00 1.00
#> 10th_C14_S53 1 0.000 0.992 1.00 0.00
#> 10th_C16_S105 2 0.000 0.978 0.00 1.00
#> 10th_C1_S59 1 0.000 0.992 1.00 0.00
#> 10th_C20_S54 1 0.000 0.992 1.00 0.00
#> 10th_C23_S98 1 0.000 0.992 1.00 0.00
#> 10th_C24_S90 2 0.000 0.978 0.00 1.00
#> 10th_C30_S107 1 0.000 0.992 1.00 0.00
#> 10th_C31_S48 1 0.000 0.992 1.00 0.00
#> 10th_C41_S101 1 0.000 0.992 1.00 0.00
#> 10th_C45_S66 1 0.000 0.992 1.00 0.00
#> 10th_C46_S94 2 0.000 0.978 0.00 1.00
#> 10th_C4_S103 2 0.000 0.978 0.00 1.00
#> 10th_C54_S124 2 0.000 0.978 0.00 1.00
#> 10th_C56_S74 2 0.000 0.978 0.00 1.00
#> 10th_C68_S75 2 0.000 0.978 0.00 1.00
#> 10th_C73_S84 2 0.000 0.978 0.00 1.00
#> 10th_C74_S76 1 0.000 0.992 1.00 0.00
#> 10th_C76_S128 1 0.000 0.992 1.00 0.00
#> 10th_C7_S60 2 0.000 0.978 0.00 1.00
#> 10th_C85_S86 1 0.000 0.992 1.00 0.00
#> 10th_C88_S130 2 0.000 0.978 0.00 1.00
#> 10th_C8_S52 1 0.000 0.992 1.00 0.00
#> 10th_C90_S116 1 0.000 0.992 1.00 0.00
#> 10th_C96_S117 1 0.000 0.992 1.00 0.00
#> 11th-C16_S64 2 0.000 0.978 0.00 1.00
#> 11th-C24_S49 2 0.000 0.978 0.00 1.00
#> 11th-C33_S20 2 0.000 0.978 0.00 1.00
#> 11th-C36_S67 2 0.000 0.978 0.00 1.00
#> 11th-C39_S21 1 0.000 0.992 1.00 0.00
#> 11th-C40_S52 2 0.000 0.978 0.00 1.00
#> 11th-C58_S71 2 0.000 0.978 0.00 1.00
#> 11th-C5_S54 1 0.000 0.992 1.00 0.00
#> 11th-C61_S25 1 0.000 0.992 1.00 0.00
#> 11th-C68_S34 2 0.000 0.978 0.00 1.00
#> 12th-C11_S147 1 0.000 0.992 1.00 0.00
#> 12th-C12_S139 1 0.000 0.992 1.00 0.00
#> 12th-C20_S191 1 0.000 0.992 1.00 0.00
#> 12th-C25_S185 1 0.000 0.992 1.00 0.00
#> 12th-C26_S192 1 0.000 0.992 1.00 0.00
#> 12th-C28_S142 1 0.000 0.992 1.00 0.00
#> 12th-C30_S157 1 0.000 0.992 1.00 0.00
#> 12th-C33_S200 1 0.000 0.992 1.00 0.00
#> 12th-C46_S145 2 0.000 0.978 0.00 1.00
#> 12th-C48_S160 1 0.000 0.992 1.00 0.00
#> 12th-C51_S217 1 0.000 0.992 1.00 0.00
#> 12th-C63_S219 1 0.000 0.992 1.00 0.00
#> 12th-C69_S135 2 0.000 0.978 0.00 1.00
#> 12th-C80_S215 1 0.000 0.992 1.00 0.00
#> 12th-C81_S207 1 0.000 0.992 1.00 0.00
#> 12th-C85_S137 1 0.000 0.992 1.00 0.00
#> 12th-C94_S180 2 0.000 0.978 0.00 1.00
#> 13th_C12_S178 1 0.000 0.992 1.00 0.00
#> 13th_C13_S149 1 0.000 0.992 1.00 0.00
#> 13th_C16_S193 1 0.000 0.992 1.00 0.00
#> 13th_C23_S187 2 0.000 0.978 0.00 1.00
#> 13th_C39_S153 1 0.000 0.992 1.00 0.00
#> 13th_C60_S213 1 0.000 0.992 1.00 0.00
#> 13th_C94_S219 1 0.000 0.992 1.00 0.00
#> 13th_C96_S204 1 0.000 0.992 1.00 0.00
#> 1st-C21_S4 1 0.000 0.992 1.00 0.00
#> 1st-C34_S54 2 0.000 0.978 0.00 1.00
#> 1st-C69_S44 1 0.000 0.992 1.00 0.00
#> 1st-C71_S83 1 0.000 0.992 1.00 0.00
#> 2nd-C25_S49 2 0.981 0.283 0.42 0.58
#> 2nd-C29_S56 1 0.000 0.992 1.00 0.00
#> 2nd-C31_S61 1 0.000 0.992 1.00 0.00
#> 2nd-C47_S92 1 0.000 0.992 1.00 0.00
#> 2nd-C54_S12 2 0.000 0.978 0.00 1.00
#> 2nd-C57_S18 1 0.000 0.992 1.00 0.00
#> 2nd-C6_S7 1 0.000 0.992 1.00 0.00
#> 2nd-C74_S53 1 0.000 0.992 1.00 0.00
#> 2nd-C76_S60 1 0.000 0.992 1.00 0.00
#> 2nd-C81_S64 1 0.000 0.992 1.00 0.00
#> 2nd-C83_S71 1 0.000 0.992 1.00 0.00
#> 3rd-C18_S80 1 0.000 0.992 1.00 0.00
#> 3rd-C1_S39 1 0.584 0.832 0.86 0.14
#> 3rd-C20_S22 2 0.000 0.978 0.00 1.00
#> 3rd-C21_S11 1 0.000 0.992 1.00 0.00
#> 3rd-C26_S28 1 0.000 0.992 1.00 0.00
#> 3rd-C40_S57 1 0.000 0.992 1.00 0.00
#> 3rd-C42_S74 2 0.000 0.978 0.00 1.00
#> 3rd-C46_S93 1 0.000 0.992 1.00 0.00
#> 3rd-C67_S69 1 0.000 0.992 1.00 0.00
#> 3rd-C68_S13 1 0.000 0.992 1.00 0.00
#> 3rd-C76_S22 1 0.000 0.992 1.00 0.00
#> 3rd-C86_S85 1 0.000 0.992 1.00 0.00
#> 3rd-C87_S88 1 0.000 0.992 1.00 0.00
#> 4th-C12_S19 1 0.000 0.992 1.00 0.00
#> 4th-C23_S44 1 0.000 0.992 1.00 0.00
#> 4th-C28_S55 1 0.000 0.992 1.00 0.00
#> 4th-C29_S56 1 0.000 0.992 1.00 0.00
#> 4th-C32_S62 1 0.000 0.992 1.00 0.00
#> 4th-C33_S63 1 0.000 0.992 1.00 0.00
#> 4th-C43_S85 2 0.000 0.978 0.00 1.00
#> 4th-C49_S4 1 0.000 0.992 1.00 0.00
#> 4th-C51_S6 1 0.000 0.992 1.00 0.00
#> 4th-C59_S23 1 0.000 0.992 1.00 0.00
#> 4th-C63_S30 1 0.000 0.992 1.00 0.00
#> 4th-C69_S42 1 0.000 0.992 1.00 0.00
#> 4th-C70_S46 2 0.000 0.978 0.00 1.00
#> 4th-C78_S58 2 0.000 0.978 0.00 1.00
#> 4th-C81_S64 2 0.000 0.978 0.00 1.00
#> 4th-C87_S76 1 0.000 0.992 1.00 0.00
#> 4th-C8_S14 1 0.000 0.992 1.00 0.00
#> 4th-C95_S95 2 0.000 0.978 0.00 1.00
#> 5th-C12_S90 2 0.000 0.978 0.00 1.00
#> 5th-C19_S104 2 0.000 0.978 0.00 1.00
#> 5th-C21_S102 1 0.000 0.992 1.00 0.00
#> 5th-C30_S105 2 0.000 0.978 0.00 1.00
#> 5th-C47_S118 2 0.000 0.978 0.00 1.00
#> 5th-C50_S90 2 0.000 0.978 0.00 1.00
#> 5th-C54_S89 2 0.000 0.978 0.00 1.00
#> 5th-C57_S96 2 0.000 0.978 0.00 1.00
#> 5th-C59_S94 2 0.000 0.978 0.00 1.00
#> 5th-C64_S99 2 0.000 0.978 0.00 1.00
#> 5th-C66_S101 2 0.529 0.858 0.12 0.88
#> 5th-C68_S106 2 0.722 0.756 0.20 0.80
#> 5th-C69_S107 2 0.855 0.624 0.28 0.72
#> 5th-C74_S110 1 0.943 0.419 0.64 0.36
#> 5th-C77_S107 2 0.760 0.726 0.22 0.78
#> 5th-C92_S124 2 0.000 0.978 0.00 1.00
#> 6th-C16_S29 1 0.000 0.992 1.00 0.00
#> 6th-C53_S10 2 0.000 0.978 0.00 1.00
#> 6th-C5_S8 1 0.000 0.992 1.00 0.00
#> 6th-C65_S31 1 0.000 0.992 1.00 0.00
#> 6th-C91_S84 1 0.000 0.992 1.00 0.00
#> 6th-C93_S82 1 0.000 0.992 1.00 0.00
#> 7th-C15_S23 1 0.000 0.992 1.00 0.00
#> 7th-C17_S29 2 0.000 0.978 0.00 1.00
#> 7th-C32_S54 1 0.000 0.992 1.00 0.00
#> 7th-C34_S59 1 0.000 0.992 1.00 0.00
#> 7th-C40_S70 2 0.000 0.978 0.00 1.00
#> 7th-C44_S76 2 0.000 0.978 0.00 1.00
#> 7th-C56_S15 2 0.000 0.978 0.00 1.00
#> 7th-C68_S38 2 0.000 0.978 0.00 1.00
#> 7th-C69_S39 1 0.000 0.992 1.00 0.00
#> 7th-C72_S42 1 0.000 0.992 1.00 0.00
#> 7th-C88_S75 2 0.000 0.978 0.00 1.00
#> 8th-C11_S99 1 0.000 0.992 1.00 0.00
#> 8th-C20_S116 1 0.000 0.992 1.00 0.00
#> 8th-C34_S141 1 0.000 0.992 1.00 0.00
#> 8th-C59_S102 1 0.000 0.992 1.00 0.00
#> 8th-C61_S107 1 0.000 0.992 1.00 0.00
#> 8th-C64_S112 1 0.000 0.992 1.00 0.00
#> 8th-C6_S88 1 0.000 0.992 1.00 0.00
#> 8th-C73_S130 2 0.000 0.978 0.00 1.00
#> 8th-C7_S95 1 0.000 0.992 1.00 0.00
#> 8th-C92_S157 1 0.943 0.426 0.64 0.36
#> 8th-C95_S161 1 0.000 0.992 1.00 0.00
#> 9th-C15_S22 1 0.000 0.992 1.00 0.00
#> 9th-C16_S30 1 0.000 0.992 1.00 0.00
#> 9th-C17_S29 1 0.000 0.992 1.00 0.00
#> 9th-C19_S36 1 0.000 0.992 1.00 0.00
#> 9th-C28_S50 1 0.000 0.992 1.00 0.00
#> 9th-C29_S51 1 0.000 0.992 1.00 0.00
#> 9th-C30_S52 1 0.000 0.992 1.00 0.00
#> 9th-C36_S59 2 0.000 0.978 0.00 1.00
#> 9th-C40_S69 2 0.000 0.978 0.00 1.00
#> 9th-C5_S8 1 0.000 0.992 1.00 0.00
#> 9th-C61_S25 2 0.000 0.978 0.00 1.00
#> 9th-C62_S26 1 0.000 0.992 1.00 0.00
#> 9th-C64_S31 1 0.000 0.992 1.00 0.00
#> 9th-C65_S32 1 0.000 0.992 1.00 0.00
#> 9th-C66_S33 1 0.141 0.972 0.98 0.02
#> 9th-C67_S37 1 0.000 0.992 1.00 0.00
#> 9th-C74_S48 1 0.000 0.992 1.00 0.00
#> 9th-C77_S53 1 0.000 0.992 1.00 0.00
#> 9th-C84_S60 2 0.000 0.978 0.00 1.00
#> 9th-C96_S81 2 0.000 0.978 0.00 1.00
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> 10th_C10_S104 3 0.0000 0.989 0.00 0.00 1.00
#> 10th_C14_S53 1 0.0000 1.000 1.00 0.00 0.00
#> 10th_C16_S105 3 0.0000 0.989 0.00 0.00 1.00
#> 10th_C1_S59 1 0.0000 1.000 1.00 0.00 0.00
#> 10th_C20_S54 3 0.0000 0.989 0.00 0.00 1.00
#> 10th_C23_S98 3 0.0000 0.989 0.00 0.00 1.00
#> 10th_C24_S90 3 0.0000 0.989 0.00 0.00 1.00
#> 10th_C30_S107 1 0.0000 1.000 1.00 0.00 0.00
#> 10th_C31_S48 1 0.0000 1.000 1.00 0.00 0.00
#> 10th_C41_S101 3 0.2537 0.897 0.08 0.00 0.92
#> 10th_C45_S66 1 0.0000 1.000 1.00 0.00 0.00
#> 10th_C46_S94 2 0.0000 0.999 0.00 1.00 0.00
#> 10th_C4_S103 2 0.0000 0.999 0.00 1.00 0.00
#> 10th_C54_S124 3 0.0000 0.989 0.00 0.00 1.00
#> 10th_C56_S74 2 0.0000 0.999 0.00 1.00 0.00
#> 10th_C68_S75 3 0.0000 0.989 0.00 0.00 1.00
#> 10th_C73_S84 2 0.0000 0.999 0.00 1.00 0.00
#> 10th_C74_S76 1 0.0000 1.000 1.00 0.00 0.00
#> 10th_C76_S128 3 0.0000 0.989 0.00 0.00 1.00
#> 10th_C7_S60 2 0.0000 0.999 0.00 1.00 0.00
#> 10th_C85_S86 1 0.0000 1.000 1.00 0.00 0.00
#> 10th_C88_S130 2 0.0000 0.999 0.00 1.00 0.00
#> 10th_C8_S52 3 0.0000 0.989 0.00 0.00 1.00
#> 10th_C90_S116 1 0.0000 1.000 1.00 0.00 0.00
#> 10th_C96_S117 1 0.0000 1.000 1.00 0.00 0.00
#> 11th-C16_S64 3 0.4002 0.809 0.00 0.16 0.84
#> 11th-C24_S49 2 0.0000 0.999 0.00 1.00 0.00
#> 11th-C33_S20 3 0.0000 0.989 0.00 0.00 1.00
#> 11th-C36_S67 3 0.0000 0.989 0.00 0.00 1.00
#> 11th-C39_S21 3 0.0000 0.989 0.00 0.00 1.00
#> 11th-C40_S52 2 0.0000 0.999 0.00 1.00 0.00
#> 11th-C58_S71 2 0.0000 0.999 0.00 1.00 0.00
#> 11th-C5_S54 1 0.0000 1.000 1.00 0.00 0.00
#> 11th-C61_S25 3 0.0000 0.989 0.00 0.00 1.00
#> 11th-C68_S34 2 0.0000 0.999 0.00 1.00 0.00
#> 12th-C11_S147 1 0.0000 1.000 1.00 0.00 0.00
#> 12th-C12_S139 3 0.0000 0.989 0.00 0.00 1.00
#> 12th-C20_S191 3 0.0000 0.989 0.00 0.00 1.00
#> 12th-C25_S185 1 0.0000 1.000 1.00 0.00 0.00
#> 12th-C26_S192 1 0.0000 1.000 1.00 0.00 0.00
#> 12th-C28_S142 1 0.0000 1.000 1.00 0.00 0.00
#> 12th-C30_S157 1 0.0000 1.000 1.00 0.00 0.00
#> 12th-C33_S200 1 0.0000 1.000 1.00 0.00 0.00
#> 12th-C46_S145 2 0.0000 0.999 0.00 1.00 0.00
#> 12th-C48_S160 1 0.0000 1.000 1.00 0.00 0.00
#> 12th-C51_S217 1 0.0000 1.000 1.00 0.00 0.00
#> 12th-C63_S219 1 0.0000 1.000 1.00 0.00 0.00
#> 12th-C69_S135 2 0.0000 0.999 0.00 1.00 0.00
#> 12th-C80_S215 1 0.0000 1.000 1.00 0.00 0.00
#> 12th-C81_S207 1 0.0000 1.000 1.00 0.00 0.00
#> 12th-C85_S137 3 0.0000 0.989 0.00 0.00 1.00
#> 12th-C94_S180 2 0.0000 0.999 0.00 1.00 0.00
#> 13th_C12_S178 1 0.0000 1.000 1.00 0.00 0.00
#> 13th_C13_S149 1 0.0000 1.000 1.00 0.00 0.00
#> 13th_C16_S193 1 0.0000 1.000 1.00 0.00 0.00
#> 13th_C23_S187 2 0.0000 0.999 0.00 1.00 0.00
#> 13th_C39_S153 3 0.0000 0.989 0.00 0.00 1.00
#> 13th_C60_S213 1 0.0000 1.000 1.00 0.00 0.00
#> 13th_C94_S219 1 0.0000 1.000 1.00 0.00 0.00
#> 13th_C96_S204 1 0.0000 1.000 1.00 0.00 0.00
#> 1st-C21_S4 1 0.0000 1.000 1.00 0.00 0.00
#> 1st-C34_S54 2 0.0000 0.999 0.00 1.00 0.00
#> 1st-C69_S44 1 0.0000 1.000 1.00 0.00 0.00
#> 1st-C71_S83 1 0.0000 1.000 1.00 0.00 0.00
#> 2nd-C25_S49 3 0.0000 0.989 0.00 0.00 1.00
#> 2nd-C29_S56 1 0.0000 1.000 1.00 0.00 0.00
#> 2nd-C31_S61 1 0.0000 1.000 1.00 0.00 0.00
#> 2nd-C47_S92 1 0.0000 1.000 1.00 0.00 0.00
#> 2nd-C54_S12 2 0.0000 0.999 0.00 1.00 0.00
#> 2nd-C57_S18 1 0.0000 1.000 1.00 0.00 0.00
#> 2nd-C6_S7 1 0.0000 1.000 1.00 0.00 0.00
#> 2nd-C74_S53 1 0.0000 1.000 1.00 0.00 0.00
#> 2nd-C76_S60 3 0.0000 0.989 0.00 0.00 1.00
#> 2nd-C81_S64 1 0.0000 1.000 1.00 0.00 0.00
#> 2nd-C83_S71 1 0.0000 1.000 1.00 0.00 0.00
#> 3rd-C18_S80 1 0.0000 1.000 1.00 0.00 0.00
#> 3rd-C1_S39 3 0.0000 0.989 0.00 0.00 1.00
#> 3rd-C20_S22 3 0.0000 0.989 0.00 0.00 1.00
#> 3rd-C21_S11 1 0.0000 1.000 1.00 0.00 0.00
#> 3rd-C26_S28 1 0.0000 1.000 1.00 0.00 0.00
#> 3rd-C40_S57 1 0.0000 1.000 1.00 0.00 0.00
#> 3rd-C42_S74 2 0.0000 0.999 0.00 1.00 0.00
#> 3rd-C46_S93 3 0.0000 0.989 0.00 0.00 1.00
#> 3rd-C67_S69 1 0.0000 1.000 1.00 0.00 0.00
#> 3rd-C68_S13 3 0.0892 0.967 0.02 0.00 0.98
#> 3rd-C76_S22 1 0.0000 1.000 1.00 0.00 0.00
#> 3rd-C86_S85 1 0.0000 1.000 1.00 0.00 0.00
#> 3rd-C87_S88 3 0.0000 0.989 0.00 0.00 1.00
#> 4th-C12_S19 1 0.0000 1.000 1.00 0.00 0.00
#> 4th-C23_S44 1 0.0000 1.000 1.00 0.00 0.00
#> 4th-C28_S55 1 0.0000 1.000 1.00 0.00 0.00
#> 4th-C29_S56 1 0.0000 1.000 1.00 0.00 0.00
#> 4th-C32_S62 1 0.0000 1.000 1.00 0.00 0.00
#> 4th-C33_S63 1 0.0000 1.000 1.00 0.00 0.00
#> 4th-C43_S85 3 0.0000 0.989 0.00 0.00 1.00
#> 4th-C49_S4 1 0.0000 1.000 1.00 0.00 0.00
#> 4th-C51_S6 1 0.0000 1.000 1.00 0.00 0.00
#> 4th-C59_S23 1 0.0000 1.000 1.00 0.00 0.00
#> 4th-C63_S30 1 0.0000 1.000 1.00 0.00 0.00
#> 4th-C69_S42 1 0.0000 1.000 1.00 0.00 0.00
#> 4th-C70_S46 3 0.0000 0.989 0.00 0.00 1.00
#> 4th-C78_S58 2 0.0000 0.999 0.00 1.00 0.00
#> 4th-C81_S64 2 0.0000 0.999 0.00 1.00 0.00
#> 4th-C87_S76 1 0.0000 1.000 1.00 0.00 0.00
#> 4th-C8_S14 1 0.0000 1.000 1.00 0.00 0.00
#> 4th-C95_S95 2 0.0000 0.999 0.00 1.00 0.00
#> 5th-C12_S90 3 0.0000 0.989 0.00 0.00 1.00
#> 5th-C19_S104 2 0.0000 0.999 0.00 1.00 0.00
#> 5th-C21_S102 2 0.1529 0.949 0.04 0.96 0.00
#> 5th-C30_S105 2 0.0000 0.999 0.00 1.00 0.00
#> 5th-C47_S118 2 0.0000 0.999 0.00 1.00 0.00
#> 5th-C50_S90 2 0.0000 0.999 0.00 1.00 0.00
#> 5th-C54_S89 2 0.0000 0.999 0.00 1.00 0.00
#> 5th-C57_S96 2 0.0000 0.999 0.00 1.00 0.00
#> 5th-C59_S94 2 0.0000 0.999 0.00 1.00 0.00
#> 5th-C64_S99 2 0.0000 0.999 0.00 1.00 0.00
#> 5th-C66_S101 2 0.0000 0.999 0.00 1.00 0.00
#> 5th-C68_S106 2 0.0000 0.999 0.00 1.00 0.00
#> 5th-C69_S107 2 0.0000 0.999 0.00 1.00 0.00
#> 5th-C74_S110 2 0.0000 0.999 0.00 1.00 0.00
#> 5th-C77_S107 2 0.0000 0.999 0.00 1.00 0.00
#> 5th-C92_S124 2 0.0000 0.999 0.00 1.00 0.00
#> 6th-C16_S29 1 0.0000 1.000 1.00 0.00 0.00
#> 6th-C53_S10 3 0.0000 0.989 0.00 0.00 1.00
#> 6th-C5_S8 1 0.0000 1.000 1.00 0.00 0.00
#> 6th-C65_S31 1 0.0000 1.000 1.00 0.00 0.00
#> 6th-C91_S84 3 0.0000 0.989 0.00 0.00 1.00
#> 6th-C93_S82 1 0.0000 1.000 1.00 0.00 0.00
#> 7th-C15_S23 1 0.0000 1.000 1.00 0.00 0.00
#> 7th-C17_S29 3 0.0000 0.989 0.00 0.00 1.00
#> 7th-C32_S54 1 0.0000 1.000 1.00 0.00 0.00
#> 7th-C34_S59 1 0.0000 1.000 1.00 0.00 0.00
#> 7th-C40_S70 2 0.0000 0.999 0.00 1.00 0.00
#> 7th-C44_S76 3 0.0000 0.989 0.00 0.00 1.00
#> 7th-C56_S15 3 0.0000 0.989 0.00 0.00 1.00
#> 7th-C68_S38 3 0.0000 0.989 0.00 0.00 1.00
#> 7th-C69_S39 1 0.0000 1.000 1.00 0.00 0.00
#> 7th-C72_S42 1 0.0000 1.000 1.00 0.00 0.00
#> 7th-C88_S75 3 0.0000 0.989 0.00 0.00 1.00
#> 8th-C11_S99 1 0.0000 1.000 1.00 0.00 0.00
#> 8th-C20_S116 3 0.0000 0.989 0.00 0.00 1.00
#> 8th-C34_S141 1 0.0000 1.000 1.00 0.00 0.00
#> 8th-C59_S102 1 0.0000 1.000 1.00 0.00 0.00
#> 8th-C61_S107 1 0.0000 1.000 1.00 0.00 0.00
#> 8th-C64_S112 1 0.0000 1.000 1.00 0.00 0.00
#> 8th-C6_S88 3 0.0000 0.989 0.00 0.00 1.00
#> 8th-C73_S130 2 0.0000 0.999 0.00 1.00 0.00
#> 8th-C7_S95 1 0.0000 1.000 1.00 0.00 0.00
#> 8th-C92_S157 3 0.0000 0.989 0.00 0.00 1.00
#> 8th-C95_S161 1 0.0000 1.000 1.00 0.00 0.00
#> 9th-C15_S22 1 0.0000 1.000 1.00 0.00 0.00
#> 9th-C16_S30 3 0.3686 0.819 0.14 0.00 0.86
#> 9th-C17_S29 1 0.0000 1.000 1.00 0.00 0.00
#> 9th-C19_S36 1 0.0892 0.979 0.98 0.00 0.02
#> 9th-C28_S50 3 0.0000 0.989 0.00 0.00 1.00
#> 9th-C29_S51 1 0.0000 1.000 1.00 0.00 0.00
#> 9th-C30_S52 1 0.0000 1.000 1.00 0.00 0.00
#> 9th-C36_S59 2 0.0000 0.999 0.00 1.00 0.00
#> 9th-C40_S69 3 0.0000 0.989 0.00 0.00 1.00
#> 9th-C5_S8 1 0.0000 1.000 1.00 0.00 0.00
#> 9th-C61_S25 2 0.0000 0.999 0.00 1.00 0.00
#> 9th-C62_S26 1 0.0000 1.000 1.00 0.00 0.00
#> 9th-C64_S31 1 0.0000 1.000 1.00 0.00 0.00
#> 9th-C65_S32 1 0.0000 1.000 1.00 0.00 0.00
#> 9th-C66_S33 3 0.0000 0.989 0.00 0.00 1.00
#> 9th-C67_S37 1 0.0000 1.000 1.00 0.00 0.00
#> 9th-C74_S48 1 0.0000 1.000 1.00 0.00 0.00
#> 9th-C77_S53 1 0.0000 1.000 1.00 0.00 0.00
#> 9th-C84_S60 2 0.0000 0.999 0.00 1.00 0.00
#> 9th-C96_S81 2 0.0000 0.999 0.00 1.00 0.00
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> 10th_C10_S104 3 0.0000 0.97383 0.00 0.00 1.00 0.00
#> 10th_C14_S53 4 0.0000 0.99158 0.00 0.00 0.00 1.00
#> 10th_C16_S105 3 0.0000 0.97383 0.00 0.00 1.00 0.00
#> 10th_C1_S59 4 0.0000 0.99158 0.00 0.00 0.00 1.00
#> 10th_C20_S54 4 0.0000 0.99158 0.00 0.00 0.00 1.00
#> 10th_C23_S98 3 0.0000 0.97383 0.00 0.00 1.00 0.00
#> 10th_C24_S90 3 0.0000 0.97383 0.00 0.00 1.00 0.00
#> 10th_C30_S107 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 10th_C31_S48 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 10th_C41_S101 3 0.5000 0.00379 0.50 0.00 0.50 0.00
#> 10th_C45_S66 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 10th_C46_S94 2 0.0000 0.99611 0.00 1.00 0.00 0.00
#> 10th_C4_S103 2 0.0000 0.99611 0.00 1.00 0.00 0.00
#> 10th_C54_S124 3 0.0000 0.97383 0.00 0.00 1.00 0.00
#> 10th_C56_S74 2 0.0000 0.99611 0.00 1.00 0.00 0.00
#> 10th_C68_S75 3 0.0000 0.97383 0.00 0.00 1.00 0.00
#> 10th_C73_S84 2 0.0000 0.99611 0.00 1.00 0.00 0.00
#> 10th_C74_S76 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 10th_C76_S128 4 0.0000 0.99158 0.00 0.00 0.00 1.00
#> 10th_C7_S60 2 0.0000 0.99611 0.00 1.00 0.00 0.00
#> 10th_C85_S86 4 0.0000 0.99158 0.00 0.00 0.00 1.00
#> 10th_C88_S130 2 0.0000 0.99611 0.00 1.00 0.00 0.00
#> 10th_C8_S52 3 0.0000 0.97383 0.00 0.00 1.00 0.00
#> 10th_C90_S116 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 10th_C96_S117 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 11th-C16_S64 3 0.0707 0.95511 0.00 0.02 0.98 0.00
#> 11th-C24_S49 2 0.0000 0.99611 0.00 1.00 0.00 0.00
#> 11th-C33_S20 3 0.0000 0.97383 0.00 0.00 1.00 0.00
#> 11th-C36_S67 3 0.0000 0.97383 0.00 0.00 1.00 0.00
#> 11th-C39_S21 3 0.0000 0.97383 0.00 0.00 1.00 0.00
#> 11th-C40_S52 2 0.0000 0.99611 0.00 1.00 0.00 0.00
#> 11th-C58_S71 2 0.0000 0.99611 0.00 1.00 0.00 0.00
#> 11th-C5_S54 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 11th-C61_S25 3 0.0000 0.97383 0.00 0.00 1.00 0.00
#> 11th-C68_S34 2 0.0000 0.99611 0.00 1.00 0.00 0.00
#> 12th-C11_S147 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 12th-C12_S139 4 0.0000 0.99158 0.00 0.00 0.00 1.00
#> 12th-C20_S191 3 0.0000 0.97383 0.00 0.00 1.00 0.00
#> 12th-C25_S185 4 0.0000 0.99158 0.00 0.00 0.00 1.00
#> 12th-C26_S192 4 0.0000 0.99158 0.00 0.00 0.00 1.00
#> 12th-C28_S142 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 12th-C30_S157 4 0.0000 0.99158 0.00 0.00 0.00 1.00
#> 12th-C33_S200 4 0.0000 0.99158 0.00 0.00 0.00 1.00
#> 12th-C46_S145 2 0.0000 0.99611 0.00 1.00 0.00 0.00
#> 12th-C48_S160 4 0.0000 0.99158 0.00 0.00 0.00 1.00
#> 12th-C51_S217 4 0.0000 0.99158 0.00 0.00 0.00 1.00
#> 12th-C63_S219 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 12th-C69_S135 2 0.0000 0.99611 0.00 1.00 0.00 0.00
#> 12th-C80_S215 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 12th-C81_S207 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 12th-C85_S137 3 0.2921 0.82507 0.00 0.00 0.86 0.14
#> 12th-C94_S180 2 0.0000 0.99611 0.00 1.00 0.00 0.00
#> 13th_C12_S178 4 0.0000 0.99158 0.00 0.00 0.00 1.00
#> 13th_C13_S149 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 13th_C16_S193 4 0.0000 0.99158 0.00 0.00 0.00 1.00
#> 13th_C23_S187 2 0.0000 0.99611 0.00 1.00 0.00 0.00
#> 13th_C39_S153 4 0.0000 0.99158 0.00 0.00 0.00 1.00
#> 13th_C60_S213 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 13th_C94_S219 4 0.0000 0.99158 0.00 0.00 0.00 1.00
#> 13th_C96_S204 4 0.0000 0.99158 0.00 0.00 0.00 1.00
#> 1st-C21_S4 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 1st-C34_S54 2 0.0000 0.99611 0.00 1.00 0.00 0.00
#> 1st-C69_S44 4 0.0000 0.99158 0.00 0.00 0.00 1.00
#> 1st-C71_S83 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 2nd-C25_S49 3 0.0000 0.97383 0.00 0.00 1.00 0.00
#> 2nd-C29_S56 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 2nd-C31_S61 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 2nd-C47_S92 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 2nd-C54_S12 2 0.0000 0.99611 0.00 1.00 0.00 0.00
#> 2nd-C57_S18 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 2nd-C6_S7 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 2nd-C74_S53 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 2nd-C76_S60 3 0.0000 0.97383 0.00 0.00 1.00 0.00
#> 2nd-C81_S64 4 0.0000 0.99158 0.00 0.00 0.00 1.00
#> 2nd-C83_S71 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 3rd-C18_S80 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 3rd-C1_S39 3 0.0000 0.97383 0.00 0.00 1.00 0.00
#> 3rd-C20_S22 3 0.0000 0.97383 0.00 0.00 1.00 0.00
#> 3rd-C21_S11 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 3rd-C26_S28 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 3rd-C40_S57 4 0.0000 0.99158 0.00 0.00 0.00 1.00
#> 3rd-C42_S74 2 0.0000 0.99611 0.00 1.00 0.00 0.00
#> 3rd-C46_S93 3 0.0000 0.97383 0.00 0.00 1.00 0.00
#> 3rd-C67_S69 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 3rd-C68_S13 4 0.0000 0.99158 0.00 0.00 0.00 1.00
#> 3rd-C76_S22 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 3rd-C86_S85 4 0.0000 0.99158 0.00 0.00 0.00 1.00
#> 3rd-C87_S88 3 0.0000 0.97383 0.00 0.00 1.00 0.00
#> 4th-C12_S19 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 4th-C23_S44 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 4th-C28_S55 4 0.0000 0.99158 0.00 0.00 0.00 1.00
#> 4th-C29_S56 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 4th-C32_S62 4 0.0000 0.99158 0.00 0.00 0.00 1.00
#> 4th-C33_S63 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 4th-C43_S85 3 0.0000 0.97383 0.00 0.00 1.00 0.00
#> 4th-C49_S4 4 0.0000 0.99158 0.00 0.00 0.00 1.00
#> 4th-C51_S6 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 4th-C59_S23 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 4th-C63_S30 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 4th-C69_S42 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 4th-C70_S46 3 0.0000 0.97383 0.00 0.00 1.00 0.00
#> 4th-C78_S58 2 0.0000 0.99611 0.00 1.00 0.00 0.00
#> 4th-C81_S64 2 0.0000 0.99611 0.00 1.00 0.00 0.00
#> 4th-C87_S76 4 0.0000 0.99158 0.00 0.00 0.00 1.00
#> 4th-C8_S14 4 0.0000 0.99158 0.00 0.00 0.00 1.00
#> 4th-C95_S95 2 0.0000 0.99611 0.00 1.00 0.00 0.00
#> 5th-C12_S90 3 0.0000 0.97383 0.00 0.00 1.00 0.00
#> 5th-C19_S104 2 0.0000 0.99611 0.00 1.00 0.00 0.00
#> 5th-C21_S102 1 0.4522 0.52601 0.68 0.32 0.00 0.00
#> 5th-C30_S105 2 0.0000 0.99611 0.00 1.00 0.00 0.00
#> 5th-C47_S118 2 0.0000 0.99611 0.00 1.00 0.00 0.00
#> 5th-C50_S90 2 0.0000 0.99611 0.00 1.00 0.00 0.00
#> 5th-C54_S89 2 0.0000 0.99611 0.00 1.00 0.00 0.00
#> 5th-C57_S96 2 0.0000 0.99611 0.00 1.00 0.00 0.00
#> 5th-C59_S94 2 0.0000 0.99611 0.00 1.00 0.00 0.00
#> 5th-C64_S99 2 0.1637 0.93681 0.00 0.94 0.00 0.06
#> 5th-C66_S101 2 0.0000 0.99611 0.00 1.00 0.00 0.00
#> 5th-C68_S106 2 0.0000 0.99611 0.00 1.00 0.00 0.00
#> 5th-C69_S107 2 0.0000 0.99611 0.00 1.00 0.00 0.00
#> 5th-C74_S110 2 0.1211 0.95379 0.04 0.96 0.00 0.00
#> 5th-C77_S107 2 0.1211 0.95379 0.04 0.96 0.00 0.00
#> 5th-C92_S124 2 0.0000 0.99611 0.00 1.00 0.00 0.00
#> 6th-C16_S29 4 0.0000 0.99158 0.00 0.00 0.00 1.00
#> 6th-C53_S10 3 0.0000 0.97383 0.00 0.00 1.00 0.00
#> 6th-C5_S8 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 6th-C65_S31 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 6th-C91_S84 4 0.4277 0.60336 0.00 0.00 0.28 0.72
#> 6th-C93_S82 4 0.0000 0.99158 0.00 0.00 0.00 1.00
#> 7th-C15_S23 4 0.0000 0.99158 0.00 0.00 0.00 1.00
#> 7th-C17_S29 3 0.0000 0.97383 0.00 0.00 1.00 0.00
#> 7th-C32_S54 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 7th-C34_S59 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 7th-C40_S70 2 0.0000 0.99611 0.00 1.00 0.00 0.00
#> 7th-C44_S76 3 0.0000 0.97383 0.00 0.00 1.00 0.00
#> 7th-C56_S15 3 0.0000 0.97383 0.00 0.00 1.00 0.00
#> 7th-C68_S38 3 0.0000 0.97383 0.00 0.00 1.00 0.00
#> 7th-C69_S39 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 7th-C72_S42 4 0.0000 0.99158 0.00 0.00 0.00 1.00
#> 7th-C88_S75 3 0.0000 0.97383 0.00 0.00 1.00 0.00
#> 8th-C11_S99 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 8th-C20_S116 3 0.0000 0.97383 0.00 0.00 1.00 0.00
#> 8th-C34_S141 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 8th-C59_S102 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 8th-C61_S107 4 0.0000 0.99158 0.00 0.00 0.00 1.00
#> 8th-C64_S112 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 8th-C6_S88 3 0.3172 0.79778 0.00 0.00 0.84 0.16
#> 8th-C73_S130 2 0.0000 0.99611 0.00 1.00 0.00 0.00
#> 8th-C7_S95 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 8th-C92_S157 3 0.0000 0.97383 0.00 0.00 1.00 0.00
#> 8th-C95_S161 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 9th-C15_S22 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 9th-C16_S30 4 0.0000 0.99158 0.00 0.00 0.00 1.00
#> 9th-C17_S29 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 9th-C19_S36 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 9th-C28_S50 3 0.0000 0.97383 0.00 0.00 1.00 0.00
#> 9th-C29_S51 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 9th-C30_S52 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 9th-C36_S59 2 0.0000 0.99611 0.00 1.00 0.00 0.00
#> 9th-C40_S69 3 0.0000 0.97383 0.00 0.00 1.00 0.00
#> 9th-C5_S8 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 9th-C61_S25 2 0.0000 0.99611 0.00 1.00 0.00 0.00
#> 9th-C62_S26 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 9th-C64_S31 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 9th-C65_S32 4 0.0000 0.99158 0.00 0.00 0.00 1.00
#> 9th-C66_S33 3 0.0000 0.97383 0.00 0.00 1.00 0.00
#> 9th-C67_S37 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 9th-C74_S48 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 9th-C77_S53 1 0.0000 0.99420 1.00 0.00 0.00 0.00
#> 9th-C84_S60 2 0.0000 0.99611 0.00 1.00 0.00 0.00
#> 9th-C96_S81 2 0.0000 0.99611 0.00 1.00 0.00 0.00
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
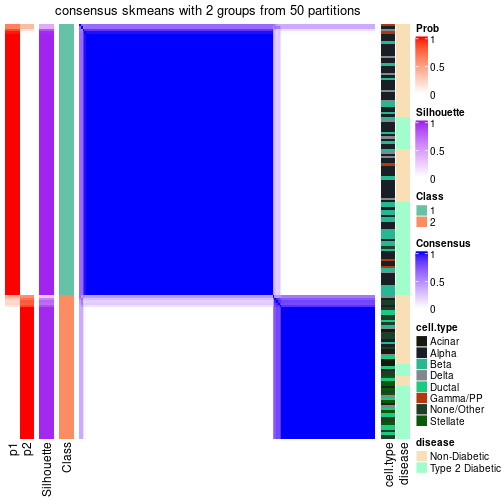
consensus_heatmap(res, k = 3)
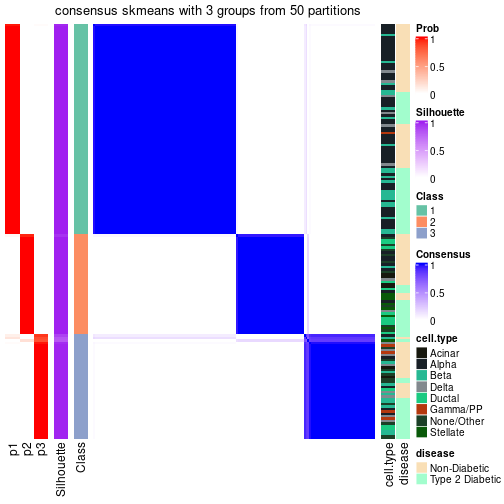
consensus_heatmap(res, k = 4)
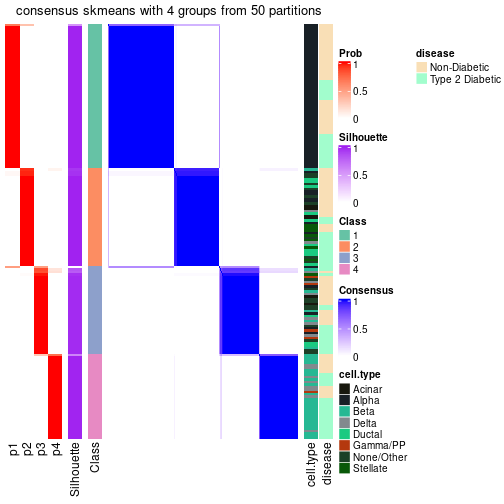
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
membership_heatmap(res, k = 3)
membership_heatmap(res, k = 4)
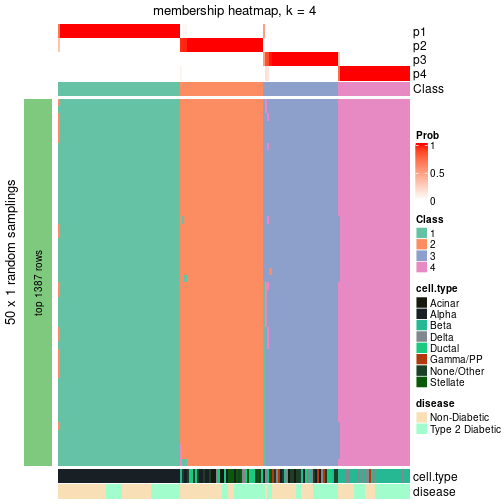
As soon as the classes for columns are determined, the signatures that are significantly different between subgroups can be looked for. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
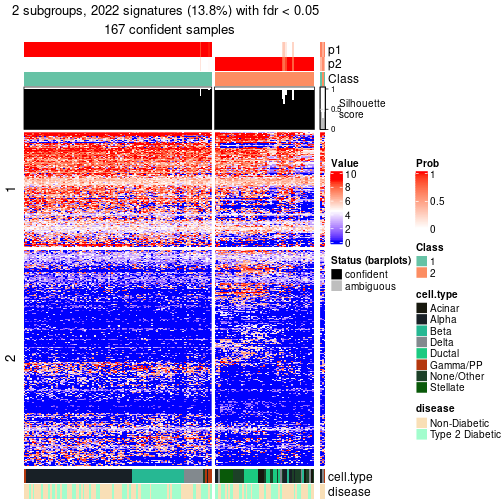
get_signatures(res, k = 3, scale_rows = FALSE)
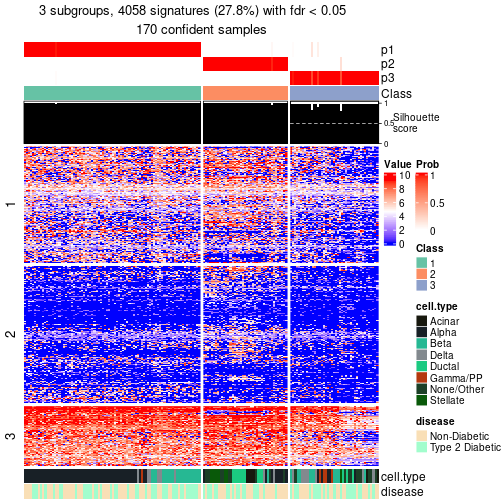
get_signatures(res, k = 4, scale_rows = FALSE)
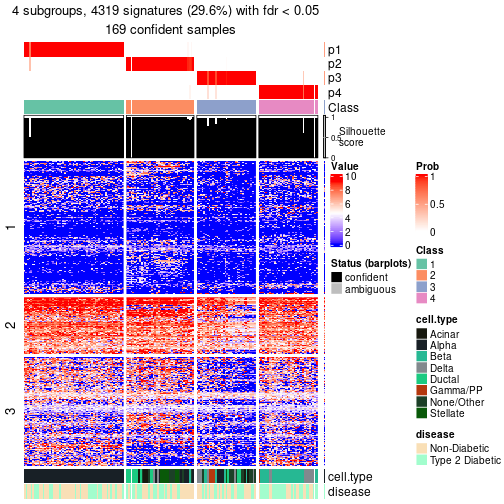
Compare the overlap of signatures from different k:
compare_signatures(res)
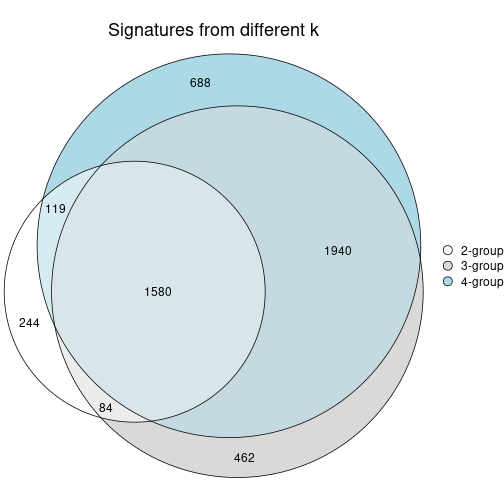
get_signature() returns a data frame invisibly. To get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows (which is done by automatically selecting number of clusters).If there are too many signatures, top_signatures = ... can be set to only show the
signatures with the highest FDRs:
# code only for demonstration
# e.g. to show the top 500 most significant rows
tb = get_signature(res, k = ..., top_signatures = 500)
If the signatures are defined as these which are uniquely high in current group, diff_method argument
can be set to "uniquely_high_in_one_group":
# code only for demonstration
tb = get_signature(res, k = ..., diff_method = "uniquely_high_in_one_group")
UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
dimension_reduction(res, k = 3, method = "UMAP")
dimension_reduction(res, k = 4, method = "UMAP")
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
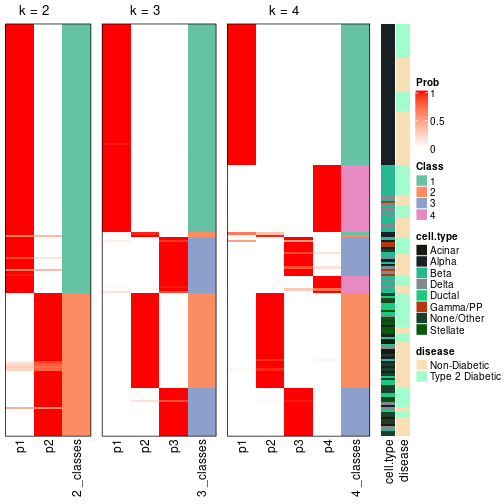
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n_sample cell.type(p-value) disease(p-value) k
#> ATC:skmeans 167 1.48e-21 1.000 2
#> ATC:skmeans 170 4.64e-18 0.784 3
#> ATC:skmeans 169 2.25e-41 0.112 4
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
Parent node: Node012. Child nodes: Node01111-leaf , Node01112-leaf , Node01121-leaf , Node01122-leaf , Node01131-leaf , Node01132 , Node01221-leaf , Node01222-leaf , Node01223-leaf , Node01231-leaf , Node01232-leaf .
The object with results only for a single top-value method and a single partitioning method can be extracted as:
res = res_rh["0122"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4.
#> On a matrix with 13596 rows and 40 columns.
#> Top rows (1360) are extracted by 'ATC' method.
#> Subgroups are detected by 'skmeans' method.
#> Performed in total 150 partitions by row resampling.
#> Best k for subgroups seems to be 3.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_partitions"
#> [7] "compare_signatures" "consensus_heatmap" "dimension_reduction"
#> [10] "functional_enrichment" "get_anno_col" "get_anno"
#> [13] "get_classes" "get_consensus" "get_matrix"
#> [16] "get_membership" "get_param" "get_signatures"
#> [19] "get_stats" "is_best_k" "is_stable_k"
#> [22] "membership_heatmap" "ncol" "nrow"
#> [25] "plot_ecdf" "predict_classes" "rownames"
#> [28] "select_partition_number" "show" "suggest_best_k"
#> [31] "test_to_known_factors" "top_rows_heatmap"
collect_plots() function collects all the plots made from res for all k (number of subgroups)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
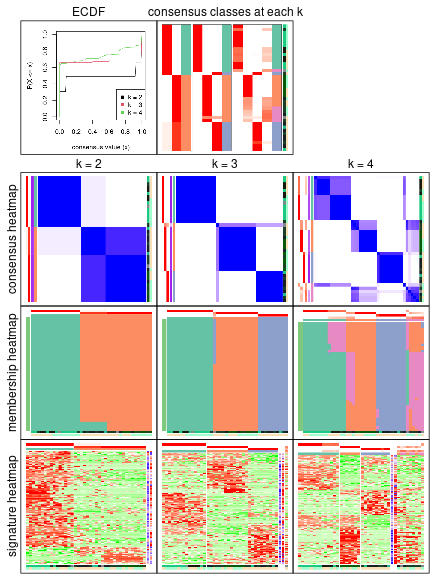
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, higher 1-PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
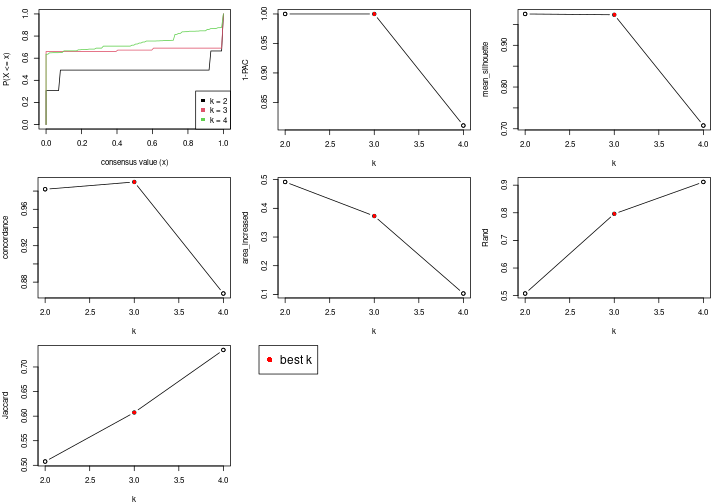
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 1.000 0.975 0.982 0.492 0.508 0.508
#> 3 3 1.000 0.973 0.990 0.373 0.796 0.607
#> 4 4 0.811 0.708 0.868 0.103 0.912 0.735
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 3
#> attr(,"optional")
#> [1] 2
There is also optional best \(k\) = 2 that is worth to check.
Following is the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall subgroup
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> 10th_C46_S94 2 0.000 0.968 0.00 1.00
#> 10th_C4_S103 1 0.000 1.000 1.00 0.00
#> 10th_C56_S74 2 0.000 0.968 0.00 1.00
#> 10th_C73_S84 1 0.000 1.000 1.00 0.00
#> 10th_C7_S60 1 0.000 1.000 1.00 0.00
#> 10th_C88_S130 1 0.000 1.000 1.00 0.00
#> 11th-C24_S49 1 0.000 1.000 1.00 0.00
#> 11th-C40_S52 2 0.000 0.968 0.00 1.00
#> 11th-C58_S71 1 0.000 1.000 1.00 0.00
#> 11th-C68_S34 1 0.000 1.000 1.00 0.00
#> 12th-C46_S145 2 0.000 0.968 0.00 1.00
#> 12th-C69_S135 2 0.000 0.968 0.00 1.00
#> 12th-C94_S180 2 0.000 0.968 0.00 1.00
#> 13th_C23_S187 2 0.000 0.968 0.00 1.00
#> 1st-C34_S54 2 0.000 0.968 0.00 1.00
#> 2nd-C54_S12 2 0.000 0.968 0.00 1.00
#> 3rd-C42_S74 2 0.000 0.968 0.00 1.00
#> 4th-C78_S58 2 0.000 0.968 0.00 1.00
#> 4th-C81_S64 1 0.000 1.000 1.00 0.00
#> 4th-C95_S95 1 0.000 1.000 1.00 0.00
#> 5th-C19_S104 1 0.000 1.000 1.00 0.00
#> 5th-C30_S105 1 0.000 1.000 1.00 0.00
#> 5th-C47_S118 2 0.000 0.968 0.00 1.00
#> 5th-C50_S90 1 0.000 1.000 1.00 0.00
#> 5th-C54_S89 1 0.000 1.000 1.00 0.00
#> 5th-C57_S96 1 0.000 1.000 1.00 0.00
#> 5th-C59_S94 2 0.402 0.943 0.08 0.92
#> 5th-C64_S99 2 0.402 0.943 0.08 0.92
#> 5th-C66_S101 2 0.402 0.943 0.08 0.92
#> 5th-C68_S106 2 0.402 0.943 0.08 0.92
#> 5th-C69_S107 2 0.402 0.943 0.08 0.92
#> 5th-C74_S110 2 0.402 0.943 0.08 0.92
#> 5th-C77_S107 2 0.402 0.943 0.08 0.92
#> 5th-C92_S124 2 0.402 0.943 0.08 0.92
#> 7th-C40_S70 2 0.000 0.968 0.00 1.00
#> 8th-C73_S130 1 0.000 1.000 1.00 0.00
#> 9th-C36_S59 2 0.000 0.968 0.00 1.00
#> 9th-C61_S25 1 0.000 1.000 1.00 0.00
#> 9th-C84_S60 2 0.402 0.943 0.08 0.92
#> 9th-C96_S81 2 0.000 0.968 0.00 1.00
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> 10th_C46_S94 2 0.000 0.971 0 1.0 0.0
#> 10th_C4_S103 1 0.000 1.000 1 0.0 0.0
#> 10th_C56_S74 2 0.000 0.971 0 1.0 0.0
#> 10th_C73_S84 1 0.000 1.000 1 0.0 0.0
#> 10th_C7_S60 1 0.000 1.000 1 0.0 0.0
#> 10th_C88_S130 1 0.000 1.000 1 0.0 0.0
#> 11th-C24_S49 1 0.000 1.000 1 0.0 0.0
#> 11th-C40_S52 2 0.000 0.971 0 1.0 0.0
#> 11th-C58_S71 1 0.000 1.000 1 0.0 0.0
#> 11th-C68_S34 1 0.000 1.000 1 0.0 0.0
#> 12th-C46_S145 2 0.000 0.971 0 1.0 0.0
#> 12th-C69_S135 2 0.000 0.971 0 1.0 0.0
#> 12th-C94_S180 2 0.000 0.971 0 1.0 0.0
#> 13th_C23_S187 2 0.000 0.971 0 1.0 0.0
#> 1st-C34_S54 2 0.000 0.971 0 1.0 0.0
#> 2nd-C54_S12 2 0.000 0.971 0 1.0 0.0
#> 3rd-C42_S74 2 0.000 0.971 0 1.0 0.0
#> 4th-C78_S58 2 0.000 0.971 0 1.0 0.0
#> 4th-C81_S64 1 0.000 1.000 1 0.0 0.0
#> 4th-C95_S95 1 0.000 1.000 1 0.0 0.0
#> 5th-C19_S104 1 0.000 1.000 1 0.0 0.0
#> 5th-C30_S105 1 0.000 1.000 1 0.0 0.0
#> 5th-C47_S118 2 0.613 0.333 0 0.6 0.4
#> 5th-C50_S90 1 0.000 1.000 1 0.0 0.0
#> 5th-C54_S89 1 0.000 1.000 1 0.0 0.0
#> 5th-C57_S96 3 0.000 1.000 0 0.0 1.0
#> 5th-C59_S94 3 0.000 1.000 0 0.0 1.0
#> 5th-C64_S99 3 0.000 1.000 0 0.0 1.0
#> 5th-C66_S101 3 0.000 1.000 0 0.0 1.0
#> 5th-C68_S106 3 0.000 1.000 0 0.0 1.0
#> 5th-C69_S107 3 0.000 1.000 0 0.0 1.0
#> 5th-C74_S110 3 0.000 1.000 0 0.0 1.0
#> 5th-C77_S107 3 0.000 1.000 0 0.0 1.0
#> 5th-C92_S124 3 0.000 1.000 0 0.0 1.0
#> 7th-C40_S70 2 0.000 0.971 0 1.0 0.0
#> 8th-C73_S130 1 0.000 1.000 1 0.0 0.0
#> 9th-C36_S59 2 0.000 0.971 0 1.0 0.0
#> 9th-C61_S25 1 0.000 1.000 1 0.0 0.0
#> 9th-C84_S60 3 0.000 1.000 0 0.0 1.0
#> 9th-C96_S81 2 0.000 0.971 0 1.0 0.0
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> 10th_C46_S94 4 0.499 0.03846 0.00 0.48 0.00 0.52
#> 10th_C4_S103 1 0.000 0.87573 1.00 0.00 0.00 0.00
#> 10th_C56_S74 2 0.000 0.77016 0.00 1.00 0.00 0.00
#> 10th_C73_S84 1 0.428 0.81515 0.72 0.00 0.00 0.28
#> 10th_C7_S60 1 0.000 0.87573 1.00 0.00 0.00 0.00
#> 10th_C88_S130 1 0.000 0.87573 1.00 0.00 0.00 0.00
#> 11th-C24_S49 1 0.000 0.87573 1.00 0.00 0.00 0.00
#> 11th-C40_S52 2 0.000 0.77016 0.00 1.00 0.00 0.00
#> 11th-C58_S71 1 0.000 0.87573 1.00 0.00 0.00 0.00
#> 11th-C68_S34 4 0.500 -0.59264 0.50 0.00 0.00 0.50
#> 12th-C46_S145 2 0.000 0.77016 0.00 1.00 0.00 0.00
#> 12th-C69_S135 4 0.452 0.48404 0.00 0.32 0.00 0.68
#> 12th-C94_S180 2 0.000 0.77016 0.00 1.00 0.00 0.00
#> 13th_C23_S187 4 0.428 0.51107 0.00 0.28 0.00 0.72
#> 1st-C34_S54 2 0.000 0.77016 0.00 1.00 0.00 0.00
#> 2nd-C54_S12 2 0.000 0.77016 0.00 1.00 0.00 0.00
#> 3rd-C42_S74 2 0.000 0.77016 0.00 1.00 0.00 0.00
#> 4th-C78_S58 2 0.499 -0.12686 0.00 0.52 0.00 0.48
#> 4th-C81_S64 1 0.000 0.87573 1.00 0.00 0.00 0.00
#> 4th-C95_S95 1 0.428 0.81515 0.72 0.00 0.00 0.28
#> 5th-C19_S104 1 0.428 0.81515 0.72 0.00 0.00 0.28
#> 5th-C30_S105 1 0.447 0.82472 0.76 0.00 0.02 0.22
#> 5th-C47_S118 4 0.559 0.46023 0.00 0.18 0.10 0.72
#> 5th-C50_S90 1 0.428 0.81515 0.72 0.00 0.00 0.28
#> 5th-C54_S89 1 0.428 0.81515 0.72 0.00 0.00 0.28
#> 5th-C57_S96 3 0.000 0.98929 0.00 0.00 1.00 0.00
#> 5th-C59_S94 3 0.000 0.98929 0.00 0.00 1.00 0.00
#> 5th-C64_S99 3 0.000 0.98929 0.00 0.00 1.00 0.00
#> 5th-C66_S101 3 0.000 0.98929 0.00 0.00 1.00 0.00
#> 5th-C68_S106 3 0.000 0.98929 0.00 0.00 1.00 0.00
#> 5th-C69_S107 3 0.000 0.98929 0.00 0.00 1.00 0.00
#> 5th-C74_S110 3 0.000 0.98929 0.00 0.00 1.00 0.00
#> 5th-C77_S107 3 0.234 0.89643 0.00 0.00 0.90 0.10
#> 5th-C92_S124 3 0.000 0.98929 0.00 0.00 1.00 0.00
#> 7th-C40_S70 4 0.452 0.49071 0.00 0.32 0.00 0.68
#> 8th-C73_S130 1 0.000 0.87573 1.00 0.00 0.00 0.00
#> 9th-C36_S59 2 0.495 0.00639 0.00 0.56 0.00 0.44
#> 9th-C61_S25 1 0.000 0.87573 1.00 0.00 0.00 0.00
#> 9th-C84_S60 3 0.000 0.98929 0.00 0.00 1.00 0.00
#> 9th-C96_S81 2 0.498 -0.05693 0.00 0.54 0.00 0.46
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)

consensus_heatmap(res, k = 3)
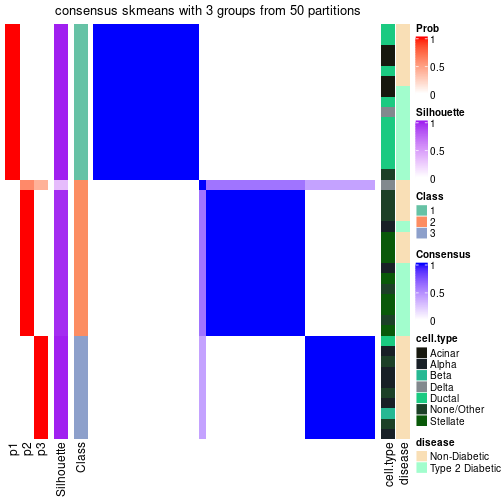
consensus_heatmap(res, k = 4)
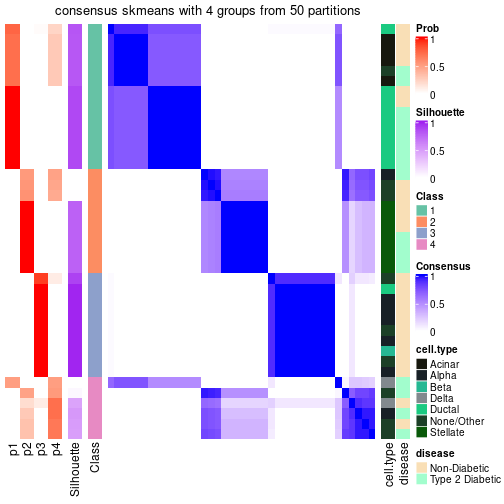
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
membership_heatmap(res, k = 3)
membership_heatmap(res, k = 4)
As soon as the classes for columns are determined, the signatures that are significantly different between subgroups can be looked for. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
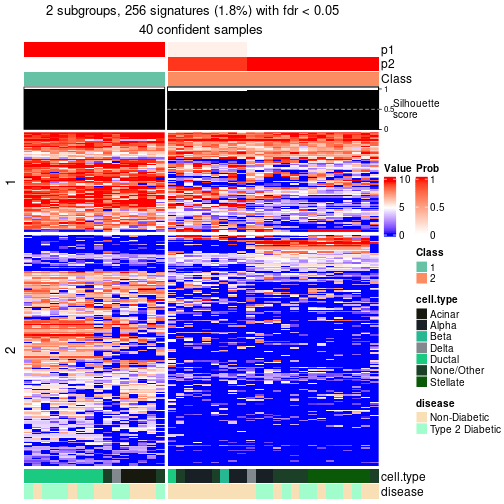
get_signatures(res, k = 3, scale_rows = FALSE)
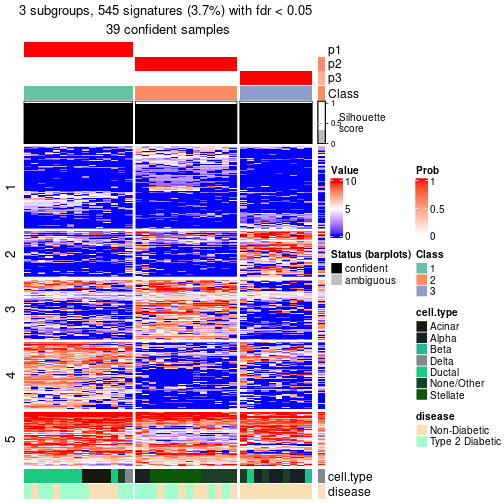
get_signatures(res, k = 4, scale_rows = FALSE)
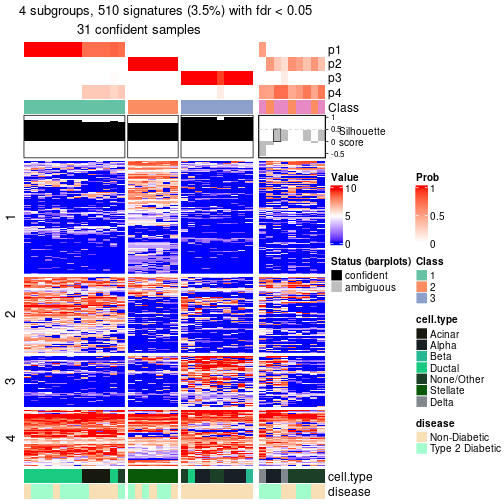
Compare the overlap of signatures from different k:
compare_signatures(res)
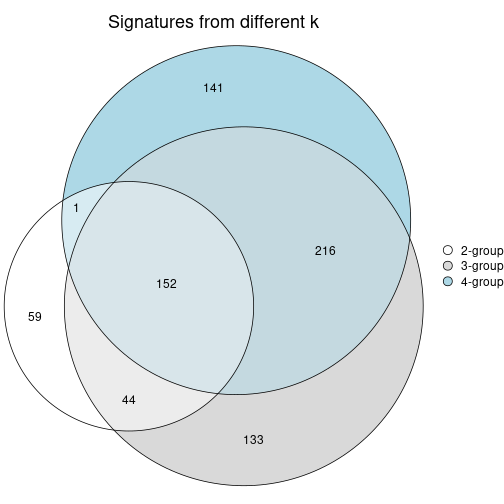
get_signature() returns a data frame invisibly. To get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows (which is done by automatically selecting number of clusters).If there are too many signatures, top_signatures = ... can be set to only show the
signatures with the highest FDRs:
# code only for demonstration
# e.g. to show the top 500 most significant rows
tb = get_signature(res, k = ..., top_signatures = 500)
If the signatures are defined as these which are uniquely high in current group, diff_method argument
can be set to "uniquely_high_in_one_group":
# code only for demonstration
tb = get_signature(res, k = ..., diff_method = "uniquely_high_in_one_group")
UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
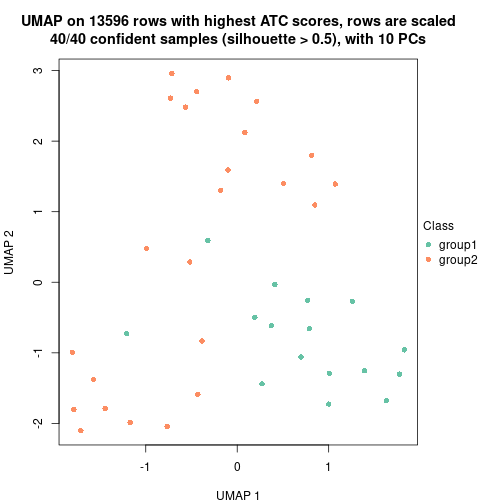
dimension_reduction(res, k = 3, method = "UMAP")
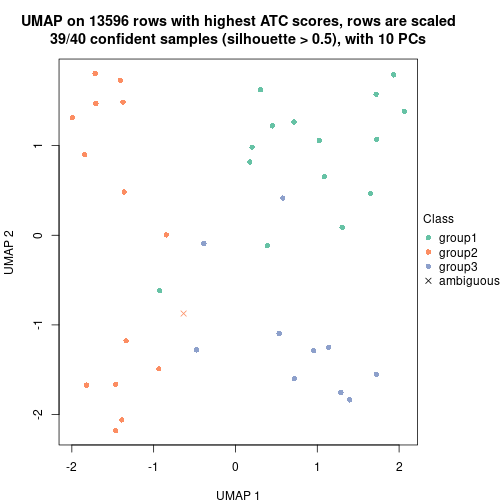
dimension_reduction(res, k = 4, method = "UMAP")
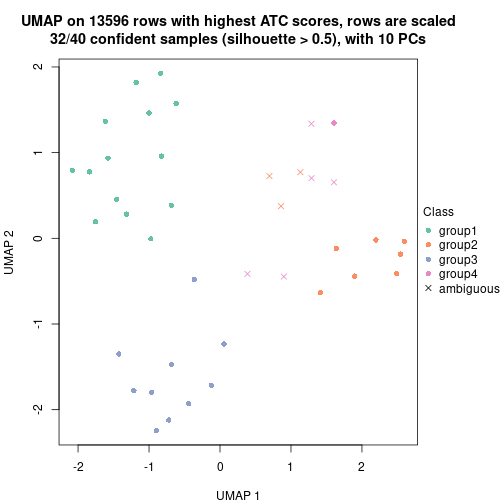
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
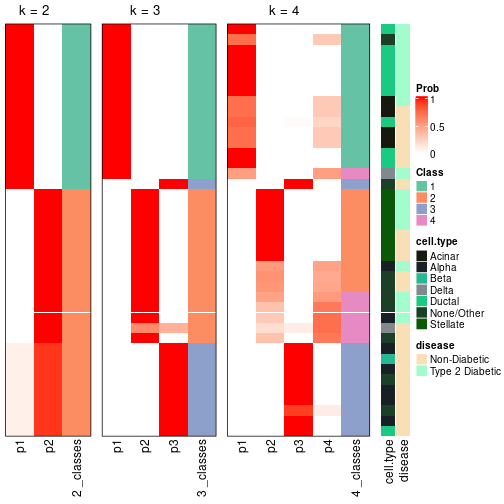
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n_sample cell.type(p-value) disease(p-value) k
#> ATC:skmeans 40 1.08e-04 0.26704 2
#> ATC:skmeans 39 6.17e-06 0.00547 3
#> ATC:skmeans 32 6.45e-07 0.01359 4
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
Parent node: Node012. Child nodes: Node01111-leaf , Node01112-leaf , Node01121-leaf , Node01122-leaf , Node01131-leaf , Node01132 , Node01221-leaf , Node01222-leaf , Node01223-leaf , Node01231-leaf , Node01232-leaf .
The object with results only for a single top-value method and a single partitioning method can be extracted as:
res = res_rh["0123"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4.
#> On a matrix with 13411 rows and 36 columns.
#> Top rows (1324) are extracted by 'ATC' method.
#> Subgroups are detected by 'skmeans' method.
#> Performed in total 150 partitions by row resampling.
#> Best k for subgroups seems to be 4.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_partitions"
#> [7] "compare_signatures" "consensus_heatmap" "dimension_reduction"
#> [10] "functional_enrichment" "get_anno_col" "get_anno"
#> [13] "get_classes" "get_consensus" "get_matrix"
#> [16] "get_membership" "get_param" "get_signatures"
#> [19] "get_stats" "is_best_k" "is_stable_k"
#> [22] "membership_heatmap" "ncol" "nrow"
#> [25] "plot_ecdf" "predict_classes" "rownames"
#> [28] "select_partition_number" "show" "suggest_best_k"
#> [31] "test_to_known_factors" "top_rows_heatmap"
collect_plots() function collects all the plots made from res for all k (number of subgroups)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
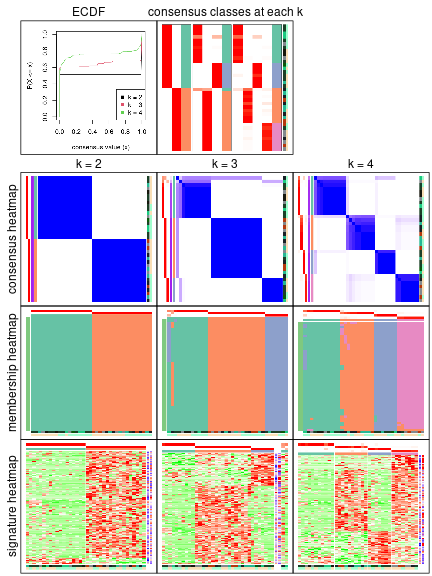
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, higher 1-PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
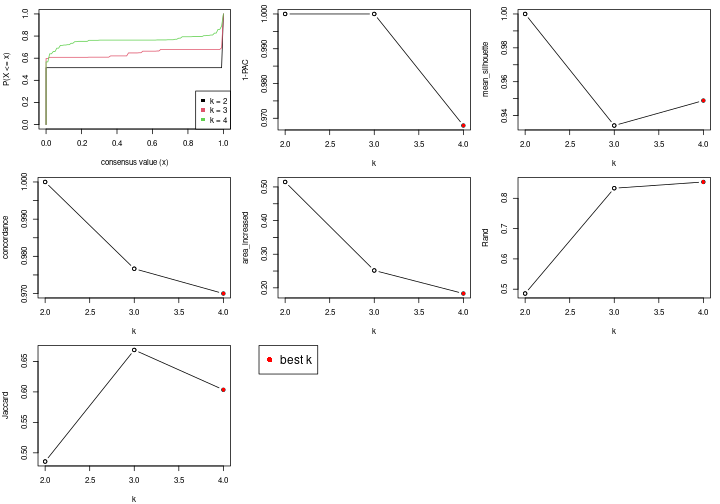
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 1.000 1.000 1.000 0.515 0.486 0.486
#> 3 3 1.000 0.934 0.977 0.252 0.833 0.669
#> 4 4 0.968 0.949 0.970 0.183 0.854 0.603
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 4
#> attr(,"optional")
#> [1] 2 3
There is also optional best \(k\) = 2 3 that is worth to check.
Following is the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall subgroup
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> 10th_C10_S104 1 0 1 1 0
#> 10th_C16_S105 1 0 1 1 0
#> 10th_C23_S98 2 0 1 0 1
#> 10th_C24_S90 1 0 1 1 0
#> 10th_C41_S101 2 0 1 0 1
#> 10th_C54_S124 1 0 1 1 0
#> 10th_C68_S75 1 0 1 1 0
#> 10th_C8_S52 2 0 1 0 1
#> 11th-C16_S64 1 0 1 1 0
#> 11th-C33_S20 1 0 1 1 0
#> 11th-C36_S67 2 0 1 0 1
#> 11th-C39_S21 2 0 1 0 1
#> 11th-C61_S25 2 0 1 0 1
#> 12th-C20_S191 2 0 1 0 1
#> 12th-C85_S137 2 0 1 0 1
#> 2nd-C25_S49 2 0 1 0 1
#> 2nd-C76_S60 2 0 1 0 1
#> 3rd-C1_S39 2 0 1 0 1
#> 3rd-C20_S22 1 0 1 1 0
#> 3rd-C46_S93 2 0 1 0 1
#> 3rd-C87_S88 2 0 1 0 1
#> 4th-C43_S85 1 0 1 1 0
#> 4th-C70_S46 1 0 1 1 0
#> 5th-C12_S90 1 0 1 1 0
#> 6th-C53_S10 1 0 1 1 0
#> 7th-C17_S29 1 0 1 1 0
#> 7th-C44_S76 1 0 1 1 0
#> 7th-C56_S15 1 0 1 1 0
#> 7th-C68_S38 1 0 1 1 0
#> 7th-C88_S75 1 0 1 1 0
#> 8th-C20_S116 2 0 1 0 1
#> 8th-C6_S88 2 0 1 0 1
#> 8th-C92_S157 2 0 1 0 1
#> 9th-C28_S50 2 0 1 0 1
#> 9th-C40_S69 1 0 1 1 0
#> 9th-C66_S33 2 0 1 0 1
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> 10th_C10_S104 1 0.0000 0.910 1.00 0.00 0.00
#> 10th_C16_S105 1 0.0000 0.910 1.00 0.00 0.00
#> 10th_C23_S98 2 0.0000 1.000 0.00 1.00 0.00
#> 10th_C24_S90 1 0.0000 0.910 1.00 0.00 0.00
#> 10th_C41_S101 2 0.0000 1.000 0.00 1.00 0.00
#> 10th_C54_S124 1 0.5948 0.401 0.64 0.00 0.36
#> 10th_C68_S75 1 0.0000 0.910 1.00 0.00 0.00
#> 10th_C8_S52 2 0.0000 1.000 0.00 1.00 0.00
#> 11th-C16_S64 3 0.0000 1.000 0.00 0.00 1.00
#> 11th-C33_S20 1 0.0000 0.910 1.00 0.00 0.00
#> 11th-C36_S67 1 0.6280 0.142 0.54 0.46 0.00
#> 11th-C39_S21 2 0.0000 1.000 0.00 1.00 0.00
#> 11th-C61_S25 2 0.0000 1.000 0.00 1.00 0.00
#> 12th-C20_S191 2 0.0000 1.000 0.00 1.00 0.00
#> 12th-C85_S137 2 0.0000 1.000 0.00 1.00 0.00
#> 2nd-C25_S49 2 0.0000 1.000 0.00 1.00 0.00
#> 2nd-C76_S60 2 0.0000 1.000 0.00 1.00 0.00
#> 3rd-C1_S39 2 0.0000 1.000 0.00 1.00 0.00
#> 3rd-C20_S22 3 0.0000 1.000 0.00 0.00 1.00
#> 3rd-C46_S93 2 0.0000 1.000 0.00 1.00 0.00
#> 3rd-C87_S88 2 0.0000 1.000 0.00 1.00 0.00
#> 4th-C43_S85 1 0.0892 0.895 0.98 0.00 0.02
#> 4th-C70_S46 3 0.0000 1.000 0.00 0.00 1.00
#> 5th-C12_S90 1 0.0000 0.910 1.00 0.00 0.00
#> 6th-C53_S10 3 0.0000 1.000 0.00 0.00 1.00
#> 7th-C17_S29 3 0.0000 1.000 0.00 0.00 1.00
#> 7th-C44_S76 1 0.0000 0.910 1.00 0.00 0.00
#> 7th-C56_S15 1 0.0000 0.910 1.00 0.00 0.00
#> 7th-C68_S38 3 0.0000 1.000 0.00 0.00 1.00
#> 7th-C88_S75 3 0.0000 1.000 0.00 0.00 1.00
#> 8th-C20_S116 2 0.0000 1.000 0.00 1.00 0.00
#> 8th-C6_S88 2 0.0000 1.000 0.00 1.00 0.00
#> 8th-C92_S157 2 0.0000 1.000 0.00 1.00 0.00
#> 9th-C28_S50 2 0.0000 1.000 0.00 1.00 0.00
#> 9th-C40_S69 1 0.0000 0.910 1.00 0.00 0.00
#> 9th-C66_S33 2 0.0000 1.000 0.00 1.00 0.00
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> 10th_C10_S104 1 0.0000 0.970 1.00 0.00 0.00 0.00
#> 10th_C16_S105 1 0.0000 0.970 1.00 0.00 0.00 0.00
#> 10th_C23_S98 2 0.0000 0.946 0.00 1.00 0.00 0.00
#> 10th_C24_S90 1 0.0000 0.970 1.00 0.00 0.00 0.00
#> 10th_C41_S101 2 0.0707 0.942 0.00 0.98 0.00 0.02
#> 10th_C54_S124 1 0.3975 0.679 0.76 0.00 0.24 0.00
#> 10th_C68_S75 1 0.0000 0.970 1.00 0.00 0.00 0.00
#> 10th_C8_S52 2 0.0000 0.946 0.00 1.00 0.00 0.00
#> 11th-C16_S64 3 0.0000 0.989 0.00 0.00 1.00 0.00
#> 11th-C33_S20 1 0.0000 0.970 1.00 0.00 0.00 0.00
#> 11th-C36_S67 2 0.5744 0.718 0.16 0.74 0.02 0.08
#> 11th-C39_S21 4 0.0707 0.988 0.00 0.02 0.00 0.98
#> 11th-C61_S25 2 0.2647 0.856 0.00 0.88 0.00 0.12
#> 12th-C20_S191 4 0.1637 0.960 0.00 0.06 0.00 0.94
#> 12th-C85_S137 2 0.0000 0.946 0.00 1.00 0.00 0.00
#> 2nd-C25_S49 4 0.0707 0.988 0.00 0.02 0.00 0.98
#> 2nd-C76_S60 2 0.1637 0.912 0.00 0.94 0.00 0.06
#> 3rd-C1_S39 4 0.0707 0.988 0.00 0.02 0.00 0.98
#> 3rd-C20_S22 3 0.0000 0.989 0.00 0.00 1.00 0.00
#> 3rd-C46_S93 2 0.0707 0.942 0.00 0.98 0.00 0.02
#> 3rd-C87_S88 2 0.0000 0.946 0.00 1.00 0.00 0.00
#> 4th-C43_S85 1 0.0707 0.959 0.98 0.00 0.00 0.02
#> 4th-C70_S46 3 0.0000 0.989 0.00 0.00 1.00 0.00
#> 5th-C12_S90 1 0.0000 0.970 1.00 0.00 0.00 0.00
#> 6th-C53_S10 3 0.1637 0.934 0.06 0.00 0.94 0.00
#> 7th-C17_S29 3 0.0000 0.989 0.00 0.00 1.00 0.00
#> 7th-C44_S76 1 0.0000 0.970 1.00 0.00 0.00 0.00
#> 7th-C56_S15 1 0.1411 0.945 0.96 0.02 0.00 0.02
#> 7th-C68_S38 3 0.0000 0.989 0.00 0.00 1.00 0.00
#> 7th-C88_S75 3 0.0000 0.989 0.00 0.00 1.00 0.00
#> 8th-C20_S116 4 0.1637 0.960 0.00 0.06 0.00 0.94
#> 8th-C6_S88 4 0.0707 0.988 0.00 0.02 0.00 0.98
#> 8th-C92_S157 4 0.0707 0.988 0.00 0.02 0.00 0.98
#> 9th-C28_S50 4 0.0707 0.988 0.00 0.02 0.00 0.98
#> 9th-C40_S69 1 0.0000 0.970 1.00 0.00 0.00 0.00
#> 9th-C66_S33 2 0.0000 0.946 0.00 1.00 0.00 0.00
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
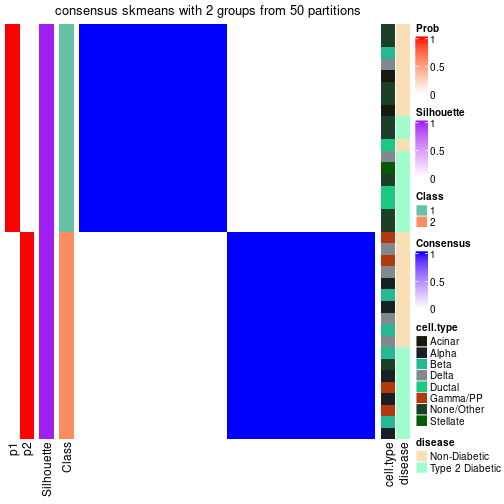
consensus_heatmap(res, k = 3)
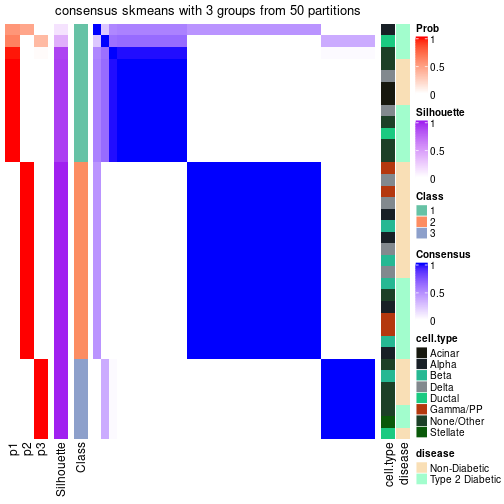
consensus_heatmap(res, k = 4)
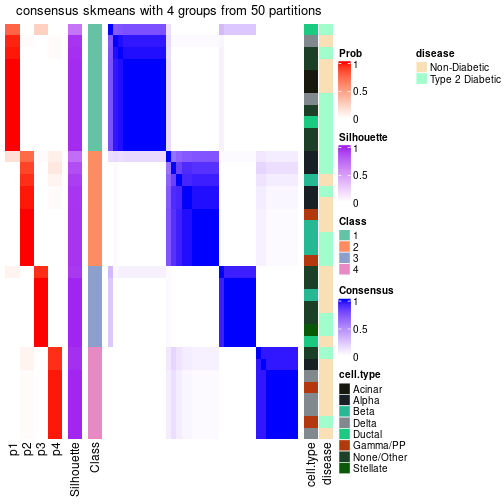
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
membership_heatmap(res, k = 3)
membership_heatmap(res, k = 4)
As soon as the classes for columns are determined, the signatures that are significantly different between subgroups can be looked for. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
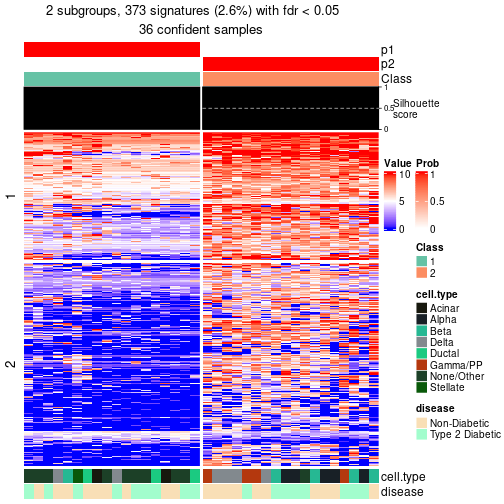
get_signatures(res, k = 3, scale_rows = FALSE)
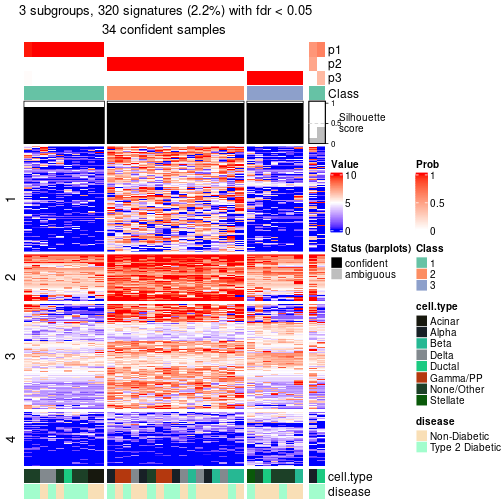
get_signatures(res, k = 4, scale_rows = FALSE)
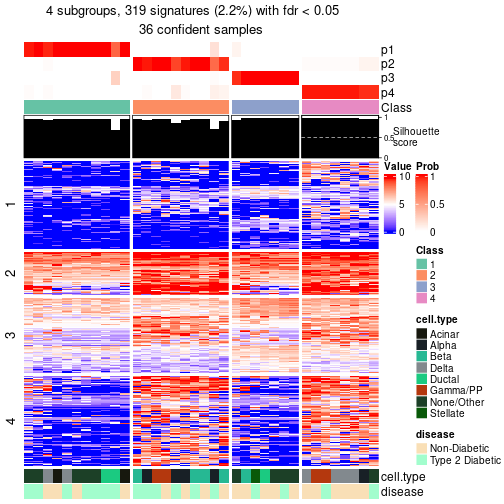
Compare the overlap of signatures from different k:
compare_signatures(res)
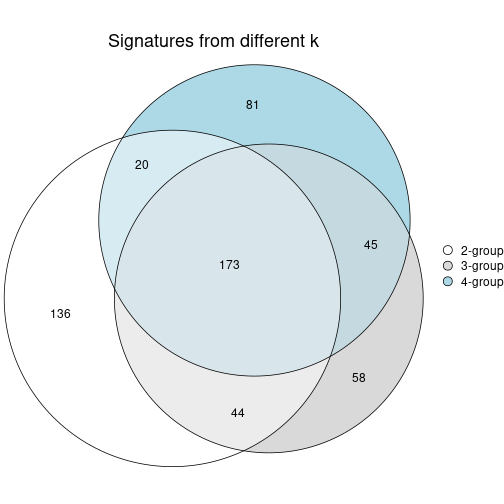
get_signature() returns a data frame invisibly. To get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows (which is done by automatically selecting number of clusters).If there are too many signatures, top_signatures = ... can be set to only show the
signatures with the highest FDRs:
# code only for demonstration
# e.g. to show the top 500 most significant rows
tb = get_signature(res, k = ..., top_signatures = 500)
If the signatures are defined as these which are uniquely high in current group, diff_method argument
can be set to "uniquely_high_in_one_group":
# code only for demonstration
tb = get_signature(res, k = ..., diff_method = "uniquely_high_in_one_group")
UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
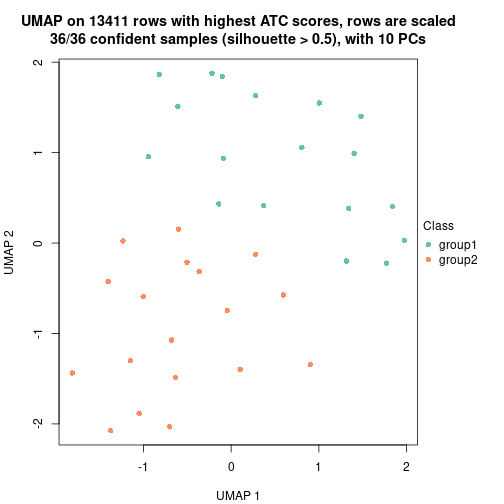
dimension_reduction(res, k = 3, method = "UMAP")
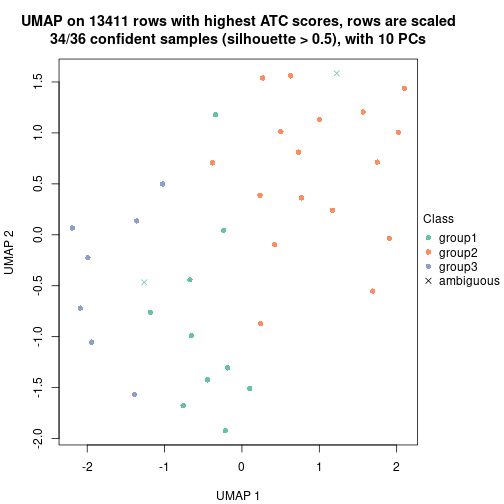
dimension_reduction(res, k = 4, method = "UMAP")
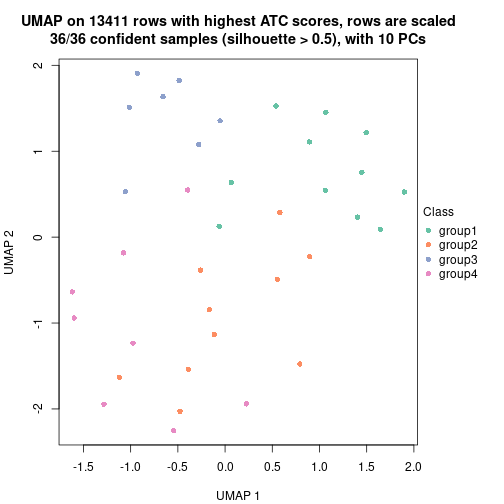
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
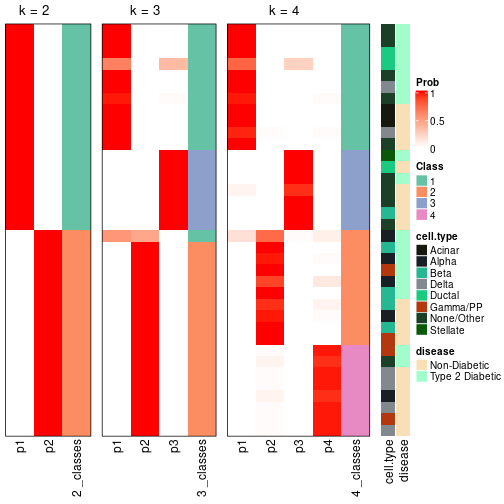
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n_sample cell.type(p-value) disease(p-value) k
#> ATC:skmeans 36 0.00120 1.000 2
#> ATC:skmeans 34 0.00973 0.413 3
#> ATC:skmeans 36 0.00133 0.221 4
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
Parent node: Node0. Child nodes: Node011 , Node012 , Node021 , Node022 , Node023 , Node024-leaf .
The object with results only for a single top-value method and a single partitioning method can be extracted as:
res = res_rh["02"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4.
#> On a matrix with 13873 rows and 261 columns.
#> Top rows (1387) are extracted by 'ATC' method.
#> Subgroups are detected by 'skmeans' method.
#> Performed in total 150 partitions by row resampling.
#> Best k for subgroups seems to be 4.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_partitions"
#> [7] "compare_signatures" "consensus_heatmap" "dimension_reduction"
#> [10] "functional_enrichment" "get_anno_col" "get_anno"
#> [13] "get_classes" "get_consensus" "get_matrix"
#> [16] "get_membership" "get_param" "get_signatures"
#> [19] "get_stats" "is_best_k" "is_stable_k"
#> [22] "membership_heatmap" "ncol" "nrow"
#> [25] "plot_ecdf" "predict_classes" "rownames"
#> [28] "select_partition_number" "show" "suggest_best_k"
#> [31] "test_to_known_factors" "top_rows_heatmap"
collect_plots() function collects all the plots made from res for all k (number of subgroups)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
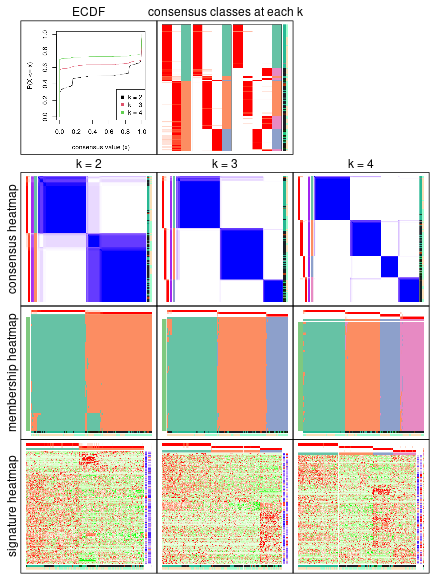
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, higher 1-PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
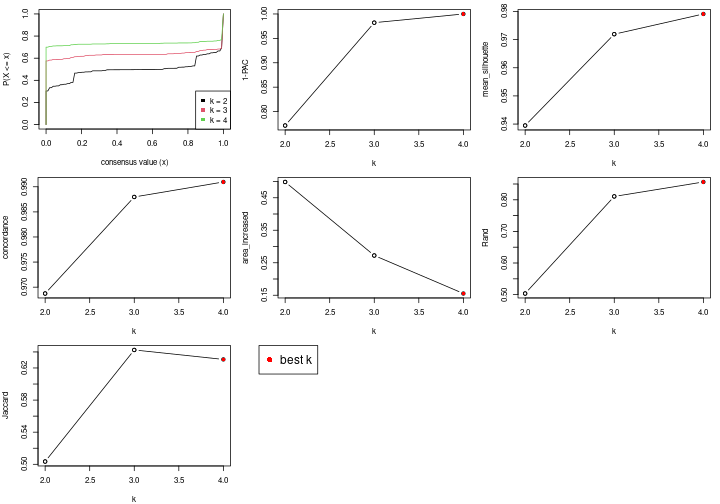
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 0.771 0.939 0.969 0.499 0.503 0.503
#> 3 3 0.982 0.972 0.988 0.272 0.811 0.642
#> 4 4 1.000 0.979 0.991 0.155 0.856 0.631
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 4
#> attr(,"optional")
#> [1] 3
There is also optional best \(k\) = 3 that is worth to check.
Following is the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall subgroup
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> 10th_C11_S96 1 0.000 0.979 1.00 0.00
#> 10th_C17_S97 1 0.000 0.979 1.00 0.00
#> 10th_C28_S91 2 0.000 0.957 0.00 1.00
#> 10th_C32_S56 1 0.000 0.979 1.00 0.00
#> 10th_C33_S64 1 0.000 0.979 1.00 0.00
#> 10th_C34_S92 2 0.000 0.957 0.00 1.00
#> 10th_C37_S49 1 0.000 0.979 1.00 0.00
#> 10th_C42_S109 2 0.634 0.842 0.16 0.84
#> 10th_C43_S50 2 0.000 0.957 0.00 1.00
#> 10th_C50_S73 2 0.000 0.957 0.00 1.00
#> 10th_C51_S80 2 0.904 0.523 0.32 0.68
#> 10th_C52_S110 2 0.000 0.957 0.00 1.00
#> 10th_C53_S118 2 0.000 0.957 0.00 1.00
#> 10th_C57_S81 2 0.000 0.957 0.00 1.00
#> 10th_C58_S111 2 0.000 0.957 0.00 1.00
#> 10th_C5_S95 2 0.000 0.957 0.00 1.00
#> 10th_C61_S68 1 0.000 0.979 1.00 0.00
#> 10th_C63_S82 2 0.242 0.934 0.04 0.96
#> 10th_C64_S112 1 0.000 0.979 1.00 0.00
#> 10th_C66_S126 1 0.000 0.979 1.00 0.00
#> 10th_C6_S88 2 0.000 0.957 0.00 1.00
#> 10th_C77_S120 2 0.634 0.842 0.16 0.84
#> 10th_C78_S114 2 0.000 0.957 0.00 1.00
#> 10th_C80_S77 2 0.634 0.842 0.16 0.84
#> 10th_C86_S78 2 0.634 0.842 0.16 0.84
#> 10th_C87_S71 2 0.634 0.842 0.16 0.84
#> 10th_C95_S123 2 0.000 0.957 0.00 1.00
#> 11th-C10_S63 2 0.000 0.957 0.00 1.00
#> 11th-C12_S47 2 0.327 0.921 0.06 0.94
#> 11th-C21_S4 1 0.000 0.979 1.00 0.00
#> 11th-C22_S65 1 0.000 0.979 1.00 0.00
#> 11th-C26_S12 2 0.242 0.934 0.04 0.96
#> 11th-C27_S19 1 0.000 0.979 1.00 0.00
#> 11th-C2_S8 2 0.634 0.842 0.16 0.84
#> 11th-C30_S66 2 0.000 0.957 0.00 1.00
#> 11th-C37_S6 2 0.000 0.957 0.00 1.00
#> 11th-C43_S7 2 0.000 0.957 0.00 1.00
#> 11th-C4_S62 2 0.000 0.957 0.00 1.00
#> 11th-C54_S86 1 0.000 0.979 1.00 0.00
#> 11th-C55_S24 2 0.000 0.957 0.00 1.00
#> 11th-C56_S32 2 0.000 0.957 0.00 1.00
#> 11th-C57_S40 1 0.634 0.821 0.84 0.16
#> 11th-C62_S33 2 0.000 0.957 0.00 1.00
#> 11th-C64_S72 2 0.634 0.842 0.16 0.84
#> 11th-C67_S26 2 0.000 0.957 0.00 1.00
#> 11th-C77_S82 2 0.634 0.842 0.16 0.84
#> 11th-C93_S30 2 0.000 0.957 0.00 1.00
#> 12th-C10_S155 1 0.000 0.979 1.00 0.00
#> 12th-C15_S183 1 0.000 0.979 1.00 0.00
#> 12th-C1_S195 2 0.000 0.957 0.00 1.00
#> 12th-C21_S184 1 0.584 0.843 0.86 0.14
#> 12th-C23_S149 2 0.000 0.957 0.00 1.00
#> 12th-C35_S151 1 0.000 0.979 1.00 0.00
#> 12th-C36_S158 2 0.634 0.842 0.16 0.84
#> 12th-C37_S187 2 0.000 0.957 0.00 1.00
#> 12th-C38_S194 1 0.000 0.979 1.00 0.00
#> 12th-C39_S201 2 0.000 0.957 0.00 1.00
#> 12th-C3_S181 1 0.000 0.979 1.00 0.00
#> 12th-C40_S144 2 0.000 0.957 0.00 1.00
#> 12th-C47_S153 1 0.000 0.979 1.00 0.00
#> 12th-C4_S154 2 0.000 0.957 0.00 1.00
#> 12th-C50_S210 2 0.000 0.957 0.00 1.00
#> 12th-C53_S168 2 0.634 0.842 0.16 0.84
#> 12th-C56_S211 2 0.634 0.842 0.16 0.84
#> 12th-C57_S218 1 0.000 0.979 1.00 0.00
#> 12th-C67_S205 1 0.584 0.845 0.86 0.14
#> 12th-C71_S171 2 0.000 0.957 0.00 1.00
#> 12th-C75_S206 2 0.000 0.957 0.00 1.00
#> 12th-C8_S189 2 0.000 0.957 0.00 1.00
#> 12th-C93_S209 1 0.000 0.979 1.00 0.00
#> 13th_C15_S134 1 0.000 0.979 1.00 0.00
#> 13th_C17_S186 2 0.000 0.957 0.00 1.00
#> 13th_C18_S179 2 0.000 0.957 0.00 1.00
#> 13th_C1_S147 2 0.000 0.957 0.00 1.00
#> 13th_C20_S142 2 0.000 0.957 0.00 1.00
#> 13th_C21_S135 2 0.000 0.957 0.00 1.00
#> 13th_C27_S151 2 0.634 0.842 0.16 0.84
#> 13th_C29_S188 2 0.000 0.957 0.00 1.00
#> 13th_C31_S137 2 0.000 0.957 0.00 1.00
#> 13th_C36_S196 2 0.634 0.842 0.16 0.84
#> 13th_C38_S145 1 0.827 0.683 0.74 0.26
#> 13th_C3_S132 2 0.000 0.957 0.00 1.00
#> 13th_C46_S183 2 0.000 0.957 0.00 1.00
#> 13th_C49_S155 2 0.000 0.957 0.00 1.00
#> 13th_C4_S191 2 0.000 0.957 0.00 1.00
#> 13th_C51_S170 2 0.000 0.957 0.00 1.00
#> 13th_C52_S198 2 0.000 0.957 0.00 1.00
#> 13th_C53_S205 2 0.000 0.957 0.00 1.00
#> 13th_C54_S212 2 0.000 0.957 0.00 1.00
#> 13th_C55_S156 2 0.000 0.957 0.00 1.00
#> 13th_C57_S171 1 0.000 0.979 1.00 0.00
#> 13th_C5_S184 2 0.000 0.957 0.00 1.00
#> 13th_C63_S172 2 0.000 0.957 0.00 1.00
#> 13th_C68_S165 2 0.000 0.957 0.00 1.00
#> 13th_C69_S173 2 0.000 0.957 0.00 1.00
#> 13th_C6_S177 2 0.000 0.957 0.00 1.00
#> 13th_C70_S201 1 0.925 0.529 0.66 0.34
#> 13th_C71_S208 1 0.634 0.821 0.84 0.16
#> 13th_C72_S215 2 0.827 0.711 0.26 0.74
#> 13th_C75_S159 1 0.000 0.979 1.00 0.00
#> 13th_C77_S209 2 0.000 0.957 0.00 1.00
#> 13th_C79_S174 2 0.000 0.957 0.00 1.00
#> 13th_C80_S167 1 0.000 0.979 1.00 0.00
#> 13th_C81_S160 1 0.529 0.867 0.88 0.12
#> 13th_C86_S168 2 0.000 0.957 0.00 1.00
#> 13th_C88_S218 2 0.000 0.957 0.00 1.00
#> 13th_C89_S211 2 0.402 0.895 0.08 0.92
#> 13th_C8_S140 2 0.141 0.946 0.02 0.98
#> 13th_C92_S169 2 0.000 0.957 0.00 1.00
#> 13th_C93_S162 2 0.000 0.957 0.00 1.00
#> 1st-C13_S19 1 0.000 0.979 1.00 0.00
#> 1st-C15_S3 2 0.000 0.957 0.00 1.00
#> 1st-C18_S51 1 0.000 0.979 1.00 0.00
#> 1st-C20_S12 1 0.242 0.947 0.96 0.04
#> 1st-C39_S23 1 0.000 0.979 1.00 0.00
#> 1st-C51_S41 1 0.634 0.821 0.84 0.16
#> 1st-C53_S74 2 0.000 0.957 0.00 1.00
#> 1st-C59_S77 1 0.141 0.964 0.98 0.02
#> 1st-C62_S35 1 0.141 0.964 0.98 0.02
#> 1st-C74_S37 2 0.000 0.957 0.00 1.00
#> 1st-C79_S46 1 0.000 0.979 1.00 0.00
#> 1st-C8_S10 2 0.000 0.957 0.00 1.00
#> 1st-C96_S94 1 0.000 0.979 1.00 0.00
#> 2nd-C19_S39 1 0.000 0.979 1.00 0.00
#> 2nd-C1_S3 2 0.000 0.957 0.00 1.00
#> 2nd-C27_S51 1 0.000 0.979 1.00 0.00
#> 2nd-C28_S55 2 0.000 0.957 0.00 1.00
#> 2nd-C2_S2 2 0.722 0.797 0.20 0.80
#> 2nd-C36_S69 1 0.141 0.964 0.98 0.02
#> 2nd-C37_S73 1 0.000 0.979 1.00 0.00
#> 2nd-C3_S1 2 0.000 0.957 0.00 1.00
#> 2nd-C49_S4 1 0.000 0.979 1.00 0.00
#> 2nd-C4_S9 2 0.760 0.719 0.22 0.78
#> 2nd-C51_S6 1 0.000 0.979 1.00 0.00
#> 2nd-C52_S10 1 0.000 0.979 1.00 0.00
#> 2nd-C58_S22 1 0.141 0.964 0.98 0.02
#> 2nd-C5_S8 1 0.000 0.979 1.00 0.00
#> 2nd-C69_S42 2 0.000 0.957 0.00 1.00
#> 2nd-C7_S15 1 0.000 0.979 1.00 0.00
#> 2nd-C87_S76 1 0.000 0.979 1.00 0.00
#> 2nd-C94_S96 2 0.000 0.957 0.00 1.00
#> 3rd-C23_S94 2 0.000 0.957 0.00 1.00
#> 3rd-C25_S15 1 0.000 0.979 1.00 0.00
#> 3rd-C32_S31 1 0.634 0.821 0.84 0.16
#> 3rd-C3_S2 1 0.141 0.964 0.98 0.02
#> 3rd-C44_S32 1 0.000 0.979 1.00 0.00
#> 3rd-C51_S87 1 0.000 0.979 1.00 0.00
#> 3rd-C52_S86 1 0.000 0.979 1.00 0.00
#> 3rd-C56_S90 1 0.000 0.979 1.00 0.00
#> 3rd-C60_S10 1 0.000 0.979 1.00 0.00
#> 3rd-C61_S64 1 0.000 0.979 1.00 0.00
#> 3rd-C63_S54 1 0.000 0.979 1.00 0.00
#> 3rd-C69_S78 2 0.141 0.944 0.02 0.98
#> 3rd-C7_S40 1 0.242 0.947 0.96 0.04
#> 3rd-C85_S83 2 0.000 0.957 0.00 1.00
#> 3rd-C96_S79 1 0.000 0.979 1.00 0.00
#> 4th-C22_S45 2 0.000 0.957 0.00 1.00
#> 4th-C27_S51 2 0.000 0.957 0.00 1.00
#> 4th-C35_S68 2 0.000 0.957 0.00 1.00
#> 4th-C37_S73 1 0.141 0.964 0.98 0.02
#> 4th-C3_S1 2 0.680 0.821 0.18 0.82
#> 4th-C45_S87 1 0.000 0.979 1.00 0.00
#> 4th-C50_S5 2 0.000 0.957 0.00 1.00
#> 4th-C57_S18 2 0.000 0.957 0.00 1.00
#> 4th-C68_S41 2 0.000 0.957 0.00 1.00
#> 4th-C93_S88 1 0.000 0.979 1.00 0.00
#> 4th-C9_S13 2 0.000 0.957 0.00 1.00
#> 5th-C10_S92 2 0.634 0.842 0.16 0.84
#> 5th-C11_S91 2 0.634 0.842 0.16 0.84
#> 5th-C14_S97 1 0.000 0.979 1.00 0.00
#> 5th-C16_S98 2 0.827 0.712 0.26 0.74
#> 5th-C18_S96 1 0.000 0.979 1.00 0.00
#> 5th-C25_S108 2 0.469 0.891 0.10 0.90
#> 5th-C40_S112 2 0.000 0.957 0.00 1.00
#> 5th-C41_S113 2 0.000 0.957 0.00 1.00
#> 5th-C42_S114 2 0.634 0.842 0.16 0.84
#> 5th-C43_S121 2 0.000 0.957 0.00 1.00
#> 5th-C45_S123 2 0.634 0.842 0.16 0.84
#> 5th-C56_S95 2 0.634 0.842 0.16 0.84
#> 5th-C58_S93 2 0.000 0.957 0.00 1.00
#> 5th-C67_S105 2 0.634 0.842 0.16 0.84
#> 5th-C6_S84 2 0.000 0.957 0.00 1.00
#> 5th-C70_S103 2 0.141 0.946 0.02 0.98
#> 5th-C73_S111 2 0.634 0.842 0.16 0.84
#> 5th-C80_S116 1 0.000 0.979 1.00 0.00
#> 5th-C81_S115 2 0.634 0.842 0.16 0.84
#> 5th-C83_S111 2 0.000 0.957 0.00 1.00
#> 5th-C87_S119 2 0.000 0.957 0.00 1.00
#> 5th-C88_S117 2 0.634 0.842 0.16 0.84
#> 6th-C15_S22 1 0.000 0.979 1.00 0.00
#> 6th-C19_S35 1 0.000 0.979 1.00 0.00
#> 6th-C1_S3 1 0.000 0.979 1.00 0.00
#> 6th-C25_S43 1 0.000 0.979 1.00 0.00
#> 6th-C28_S49 1 0.000 0.979 1.00 0.00
#> 6th-C34_S61 2 0.000 0.957 0.00 1.00
#> 6th-C45_S81 2 0.000 0.957 0.00 1.00
#> 6th-C57_S17 1 0.000 0.979 1.00 0.00
#> 6th-C58_S20 1 0.000 0.979 1.00 0.00
#> 6th-C62_S25 1 0.000 0.979 1.00 0.00
#> 6th-C64_S30 1 0.000 0.979 1.00 0.00
#> 6th-C67_S36 1 0.000 0.979 1.00 0.00
#> 6th-C82_S66 1 0.000 0.979 1.00 0.00
#> 6th-C83_S65 2 0.000 0.957 0.00 1.00
#> 6th-C84_S64 1 0.000 0.979 1.00 0.00
#> 6th-C89_S77 1 0.000 0.979 1.00 0.00
#> 6th-C90_S76 1 0.000 0.979 1.00 0.00
#> 6th-C9_S12 2 0.000 0.957 0.00 1.00
#> 7th-C12_S17 1 0.000 0.979 1.00 0.00
#> 7th-C19_S36 1 0.000 0.979 1.00 0.00
#> 7th-C1_S3 1 0.000 0.979 1.00 0.00
#> 7th-C20_S35 1 0.000 0.979 1.00 0.00
#> 7th-C21_S34 1 0.000 0.979 1.00 0.00
#> 7th-C28_S48 1 0.000 0.979 1.00 0.00
#> 7th-C2_S2 1 0.000 0.979 1.00 0.00
#> 7th-C3_S1 1 0.000 0.979 1.00 0.00
#> 7th-C47_S81 2 0.000 0.957 0.00 1.00
#> 7th-C49_S4 2 0.000 0.957 0.00 1.00
#> 7th-C4_S8 1 0.000 0.979 1.00 0.00
#> 7th-C52_S9 1 0.000 0.979 1.00 0.00
#> 7th-C57_S16 1 0.000 0.979 1.00 0.00
#> 7th-C60_S22 1 0.000 0.979 1.00 0.00
#> 7th-C65_S32 1 0.000 0.979 1.00 0.00
#> 7th-C76_S52 1 0.000 0.979 1.00 0.00
#> 7th-C81_S56 2 0.000 0.957 0.00 1.00
#> 7th-C85_S69 2 0.000 0.957 0.00 1.00
#> 7th-C94_S83 1 0.000 0.979 1.00 0.00
#> 8th-C18_S110 2 0.000 0.957 0.00 1.00
#> 8th-C21_S115 2 0.000 0.957 0.00 1.00
#> 8th-C23_S121 1 0.634 0.821 0.84 0.16
#> 8th-C26_S126 2 0.000 0.957 0.00 1.00
#> 8th-C28_S131 2 0.925 0.478 0.34 0.66
#> 8th-C37_S146 2 0.000 0.957 0.00 1.00
#> 8th-C38_S147 1 0.402 0.908 0.92 0.08
#> 8th-C47_S160 1 0.000 0.979 1.00 0.00
#> 8th-C69_S119 2 0.000 0.957 0.00 1.00
#> 8th-C70_S123 1 0.000 0.979 1.00 0.00
#> 8th-C75_S128 1 0.000 0.979 1.00 0.00
#> 8th-C79_S140 2 0.000 0.957 0.00 1.00
#> 8th-C84_S143 1 0.000 0.979 1.00 0.00
#> 8th-C90_S152 2 0.000 0.957 0.00 1.00
#> 8th-C91_S158 2 0.000 0.957 0.00 1.00
#> 8th-C94_S162 1 0.634 0.821 0.84 0.16
#> 9th-C13_S24 1 0.000 0.979 1.00 0.00
#> 9th-C14_S23 1 0.000 0.979 1.00 0.00
#> 9th-C20_S35 2 0.000 0.957 0.00 1.00
#> 9th-C22_S41 2 0.000 0.957 0.00 1.00
#> 9th-C25_S45 1 0.000 0.979 1.00 0.00
#> 9th-C2_S2 2 0.634 0.842 0.16 0.84
#> 9th-C49_S4 1 0.000 0.979 1.00 0.00
#> 9th-C51_S6 1 0.000 0.979 1.00 0.00
#> 9th-C52_S10 2 0.000 0.957 0.00 1.00
#> 9th-C59_S20 1 0.000 0.979 1.00 0.00
#> 9th-C69_S39 1 0.000 0.979 1.00 0.00
#> 9th-C75_S47 1 0.000 0.979 1.00 0.00
#> 9th-C79_S57 1 0.402 0.908 0.92 0.08
#> 9th-C85_S68 2 0.000 0.957 0.00 1.00
#> 9th-C87_S66 2 0.000 0.957 0.00 1.00
#> 9th-C88_S73 1 0.000 0.979 1.00 0.00
#> 9th-C91_S78 1 0.000 0.979 1.00 0.00
#> 9th-C92_S77 2 0.000 0.957 0.00 1.00
#> 9th-C94_S83 1 0.000 0.979 1.00 0.00
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> 10th_C11_S96 1 0.0000 0.979 1.00 0.00 0.00
#> 10th_C17_S97 1 0.0000 0.979 1.00 0.00 0.00
#> 10th_C28_S91 2 0.0000 0.992 0.00 1.00 0.00
#> 10th_C32_S56 1 0.0892 0.961 0.98 0.00 0.02
#> 10th_C33_S64 1 0.0000 0.979 1.00 0.00 0.00
#> 10th_C34_S92 2 0.0000 0.992 0.00 1.00 0.00
#> 10th_C37_S49 1 0.0000 0.979 1.00 0.00 0.00
#> 10th_C42_S109 3 0.0000 0.990 0.00 0.00 1.00
#> 10th_C43_S50 2 0.0000 0.992 0.00 1.00 0.00
#> 10th_C50_S73 2 0.0000 0.992 0.00 1.00 0.00
#> 10th_C51_S80 2 0.0892 0.970 0.02 0.98 0.00
#> 10th_C52_S110 2 0.0000 0.992 0.00 1.00 0.00
#> 10th_C53_S118 2 0.0000 0.992 0.00 1.00 0.00
#> 10th_C57_S81 2 0.0000 0.992 0.00 1.00 0.00
#> 10th_C58_S111 2 0.0000 0.992 0.00 1.00 0.00
#> 10th_C5_S95 2 0.0000 0.992 0.00 1.00 0.00
#> 10th_C61_S68 1 0.0000 0.979 1.00 0.00 0.00
#> 10th_C63_S82 3 0.0000 0.990 0.00 0.00 1.00
#> 10th_C64_S112 1 0.0000 0.979 1.00 0.00 0.00
#> 10th_C66_S126 1 0.0000 0.979 1.00 0.00 0.00
#> 10th_C6_S88 2 0.0000 0.992 0.00 1.00 0.00
#> 10th_C77_S120 3 0.0000 0.990 0.00 0.00 1.00
#> 10th_C78_S114 2 0.0000 0.992 0.00 1.00 0.00
#> 10th_C80_S77 3 0.0000 0.990 0.00 0.00 1.00
#> 10th_C86_S78 3 0.0000 0.990 0.00 0.00 1.00
#> 10th_C87_S71 3 0.0000 0.990 0.00 0.00 1.00
#> 10th_C95_S123 2 0.0000 0.992 0.00 1.00 0.00
#> 11th-C10_S63 2 0.0000 0.992 0.00 1.00 0.00
#> 11th-C12_S47 2 0.4002 0.808 0.00 0.84 0.16
#> 11th-C21_S4 1 0.0000 0.979 1.00 0.00 0.00
#> 11th-C22_S65 1 0.0000 0.979 1.00 0.00 0.00
#> 11th-C26_S12 3 0.0000 0.990 0.00 0.00 1.00
#> 11th-C27_S19 1 0.0000 0.979 1.00 0.00 0.00
#> 11th-C2_S8 3 0.0000 0.990 0.00 0.00 1.00
#> 11th-C30_S66 2 0.0000 0.992 0.00 1.00 0.00
#> 11th-C37_S6 2 0.0000 0.992 0.00 1.00 0.00
#> 11th-C43_S7 3 0.0000 0.990 0.00 0.00 1.00
#> 11th-C4_S62 3 0.0000 0.990 0.00 0.00 1.00
#> 11th-C54_S86 1 0.0000 0.979 1.00 0.00 0.00
#> 11th-C55_S24 3 0.0000 0.990 0.00 0.00 1.00
#> 11th-C56_S32 3 0.0000 0.990 0.00 0.00 1.00
#> 11th-C57_S40 2 0.0000 0.992 0.00 1.00 0.00
#> 11th-C62_S33 2 0.0000 0.992 0.00 1.00 0.00
#> 11th-C64_S72 3 0.0000 0.990 0.00 0.00 1.00
#> 11th-C67_S26 2 0.0000 0.992 0.00 1.00 0.00
#> 11th-C77_S82 3 0.0000 0.990 0.00 0.00 1.00
#> 11th-C93_S30 2 0.0000 0.992 0.00 1.00 0.00
#> 12th-C10_S155 1 0.0000 0.979 1.00 0.00 0.00
#> 12th-C15_S183 1 0.0000 0.979 1.00 0.00 0.00
#> 12th-C1_S195 2 0.0000 0.992 0.00 1.00 0.00
#> 12th-C21_S184 1 0.4796 0.713 0.78 0.22 0.00
#> 12th-C23_S149 2 0.0000 0.992 0.00 1.00 0.00
#> 12th-C35_S151 1 0.0000 0.979 1.00 0.00 0.00
#> 12th-C36_S158 3 0.0000 0.990 0.00 0.00 1.00
#> 12th-C37_S187 2 0.0000 0.992 0.00 1.00 0.00
#> 12th-C38_S194 1 0.0000 0.979 1.00 0.00 0.00
#> 12th-C39_S201 2 0.0000 0.992 0.00 1.00 0.00
#> 12th-C3_S181 1 0.0000 0.979 1.00 0.00 0.00
#> 12th-C40_S144 2 0.0000 0.992 0.00 1.00 0.00
#> 12th-C47_S153 1 0.0000 0.979 1.00 0.00 0.00
#> 12th-C4_S154 2 0.0000 0.992 0.00 1.00 0.00
#> 12th-C50_S210 2 0.0000 0.992 0.00 1.00 0.00
#> 12th-C53_S168 3 0.0000 0.990 0.00 0.00 1.00
#> 12th-C56_S211 3 0.0000 0.990 0.00 0.00 1.00
#> 12th-C57_S218 1 0.0000 0.979 1.00 0.00 0.00
#> 12th-C67_S205 1 0.0000 0.979 1.00 0.00 0.00
#> 12th-C71_S171 2 0.0000 0.992 0.00 1.00 0.00
#> 12th-C75_S206 2 0.0000 0.992 0.00 1.00 0.00
#> 12th-C8_S189 2 0.0000 0.992 0.00 1.00 0.00
#> 12th-C93_S209 1 0.0000 0.979 1.00 0.00 0.00
#> 13th_C15_S134 1 0.0000 0.979 1.00 0.00 0.00
#> 13th_C17_S186 2 0.0000 0.992 0.00 1.00 0.00
#> 13th_C18_S179 2 0.0000 0.992 0.00 1.00 0.00
#> 13th_C1_S147 2 0.0000 0.992 0.00 1.00 0.00
#> 13th_C20_S142 2 0.0000 0.992 0.00 1.00 0.00
#> 13th_C21_S135 2 0.0000 0.992 0.00 1.00 0.00
#> 13th_C27_S151 3 0.0000 0.990 0.00 0.00 1.00
#> 13th_C29_S188 2 0.0000 0.992 0.00 1.00 0.00
#> 13th_C31_S137 2 0.0000 0.992 0.00 1.00 0.00
#> 13th_C36_S196 3 0.0000 0.990 0.00 0.00 1.00
#> 13th_C38_S145 2 0.1529 0.946 0.04 0.96 0.00
#> 13th_C3_S132 2 0.0000 0.992 0.00 1.00 0.00
#> 13th_C46_S183 2 0.0000 0.992 0.00 1.00 0.00
#> 13th_C49_S155 3 0.0000 0.990 0.00 0.00 1.00
#> 13th_C4_S191 2 0.0000 0.992 0.00 1.00 0.00
#> 13th_C51_S170 2 0.0000 0.992 0.00 1.00 0.00
#> 13th_C52_S198 2 0.0000 0.992 0.00 1.00 0.00
#> 13th_C53_S205 2 0.0000 0.992 0.00 1.00 0.00
#> 13th_C54_S212 2 0.0000 0.992 0.00 1.00 0.00
#> 13th_C55_S156 2 0.0000 0.992 0.00 1.00 0.00
#> 13th_C57_S171 1 0.0000 0.979 1.00 0.00 0.00
#> 13th_C5_S184 2 0.0000 0.992 0.00 1.00 0.00
#> 13th_C63_S172 2 0.0000 0.992 0.00 1.00 0.00
#> 13th_C68_S165 2 0.0000 0.992 0.00 1.00 0.00
#> 13th_C69_S173 2 0.0000 0.992 0.00 1.00 0.00
#> 13th_C6_S177 2 0.0000 0.992 0.00 1.00 0.00
#> 13th_C70_S201 2 0.0000 0.992 0.00 1.00 0.00
#> 13th_C71_S208 2 0.4002 0.792 0.16 0.84 0.00
#> 13th_C72_S215 3 0.0000 0.990 0.00 0.00 1.00
#> 13th_C75_S159 1 0.0000 0.979 1.00 0.00 0.00
#> 13th_C77_S209 2 0.0000 0.992 0.00 1.00 0.00
#> 13th_C79_S174 2 0.0000 0.992 0.00 1.00 0.00
#> 13th_C80_S167 1 0.0000 0.979 1.00 0.00 0.00
#> 13th_C81_S160 1 0.0000 0.979 1.00 0.00 0.00
#> 13th_C86_S168 2 0.0000 0.992 0.00 1.00 0.00
#> 13th_C88_S218 2 0.0000 0.992 0.00 1.00 0.00
#> 13th_C89_S211 2 0.0000 0.992 0.00 1.00 0.00
#> 13th_C8_S140 3 0.0000 0.990 0.00 0.00 1.00
#> 13th_C92_S169 2 0.0000 0.992 0.00 1.00 0.00
#> 13th_C93_S162 2 0.0000 0.992 0.00 1.00 0.00
#> 1st-C13_S19 1 0.0000 0.979 1.00 0.00 0.00
#> 1st-C15_S3 2 0.0000 0.992 0.00 1.00 0.00
#> 1st-C18_S51 1 0.0000 0.979 1.00 0.00 0.00
#> 1st-C20_S12 1 0.5016 0.696 0.76 0.24 0.00
#> 1st-C39_S23 1 0.0000 0.979 1.00 0.00 0.00
#> 1st-C51_S41 2 0.0892 0.970 0.02 0.98 0.00
#> 1st-C53_S74 2 0.0000 0.992 0.00 1.00 0.00
#> 1st-C59_S77 1 0.3686 0.828 0.86 0.14 0.00
#> 1st-C62_S35 1 0.3686 0.828 0.86 0.14 0.00
#> 1st-C74_S37 2 0.0000 0.992 0.00 1.00 0.00
#> 1st-C79_S46 1 0.0000 0.979 1.00 0.00 0.00
#> 1st-C8_S10 2 0.0000 0.992 0.00 1.00 0.00
#> 1st-C96_S94 1 0.0000 0.979 1.00 0.00 0.00
#> 2nd-C19_S39 1 0.0000 0.979 1.00 0.00 0.00
#> 2nd-C1_S3 2 0.0000 0.992 0.00 1.00 0.00
#> 2nd-C27_S51 1 0.0000 0.979 1.00 0.00 0.00
#> 2nd-C28_S55 2 0.0000 0.992 0.00 1.00 0.00
#> 2nd-C2_S2 3 0.0000 0.990 0.00 0.00 1.00
#> 2nd-C36_S69 1 0.3686 0.828 0.86 0.14 0.00
#> 2nd-C37_S73 1 0.0000 0.979 1.00 0.00 0.00
#> 2nd-C3_S1 2 0.0000 0.992 0.00 1.00 0.00
#> 2nd-C49_S4 1 0.0000 0.979 1.00 0.00 0.00
#> 2nd-C4_S9 2 0.0000 0.992 0.00 1.00 0.00
#> 2nd-C51_S6 1 0.0000 0.979 1.00 0.00 0.00
#> 2nd-C52_S10 1 0.0000 0.979 1.00 0.00 0.00
#> 2nd-C58_S22 1 0.2959 0.875 0.90 0.10 0.00
#> 2nd-C5_S8 1 0.0000 0.979 1.00 0.00 0.00
#> 2nd-C69_S42 2 0.0000 0.992 0.00 1.00 0.00
#> 2nd-C7_S15 1 0.0000 0.979 1.00 0.00 0.00
#> 2nd-C87_S76 1 0.0000 0.979 1.00 0.00 0.00
#> 2nd-C94_S96 2 0.0000 0.992 0.00 1.00 0.00
#> 3rd-C23_S94 2 0.0000 0.992 0.00 1.00 0.00
#> 3rd-C25_S15 1 0.0000 0.979 1.00 0.00 0.00
#> 3rd-C32_S31 2 0.0000 0.992 0.00 1.00 0.00
#> 3rd-C3_S2 1 0.2959 0.875 0.90 0.10 0.00
#> 3rd-C44_S32 1 0.0000 0.979 1.00 0.00 0.00
#> 3rd-C51_S87 3 0.0000 0.990 0.00 0.00 1.00
#> 3rd-C52_S86 1 0.0000 0.979 1.00 0.00 0.00
#> 3rd-C56_S90 1 0.0000 0.979 1.00 0.00 0.00
#> 3rd-C60_S10 1 0.0000 0.979 1.00 0.00 0.00
#> 3rd-C61_S64 1 0.0000 0.979 1.00 0.00 0.00
#> 3rd-C63_S54 1 0.0000 0.979 1.00 0.00 0.00
#> 3rd-C69_S78 2 0.0000 0.992 0.00 1.00 0.00
#> 3rd-C7_S40 1 0.5706 0.555 0.68 0.32 0.00
#> 3rd-C85_S83 2 0.0000 0.992 0.00 1.00 0.00
#> 3rd-C96_S79 1 0.0000 0.979 1.00 0.00 0.00
#> 4th-C22_S45 2 0.0000 0.992 0.00 1.00 0.00
#> 4th-C27_S51 3 0.0000 0.990 0.00 0.00 1.00
#> 4th-C35_S68 2 0.0000 0.992 0.00 1.00 0.00
#> 4th-C37_S73 1 0.4002 0.804 0.84 0.16 0.00
#> 4th-C3_S1 3 0.0000 0.990 0.00 0.00 1.00
#> 4th-C45_S87 1 0.0000 0.979 1.00 0.00 0.00
#> 4th-C50_S5 2 0.0000 0.992 0.00 1.00 0.00
#> 4th-C57_S18 3 0.4291 0.782 0.00 0.18 0.82
#> 4th-C68_S41 2 0.0000 0.992 0.00 1.00 0.00
#> 4th-C93_S88 1 0.0000 0.979 1.00 0.00 0.00
#> 4th-C9_S13 2 0.0000 0.992 0.00 1.00 0.00
#> 5th-C10_S92 3 0.0000 0.990 0.00 0.00 1.00
#> 5th-C11_S91 3 0.0000 0.990 0.00 0.00 1.00
#> 5th-C14_S97 1 0.0000 0.979 1.00 0.00 0.00
#> 5th-C16_S98 3 0.0000 0.990 0.00 0.00 1.00
#> 5th-C18_S96 1 0.0000 0.979 1.00 0.00 0.00
#> 5th-C25_S108 3 0.0000 0.990 0.00 0.00 1.00
#> 5th-C40_S112 3 0.0000 0.990 0.00 0.00 1.00
#> 5th-C41_S113 2 0.3340 0.859 0.00 0.88 0.12
#> 5th-C42_S114 3 0.0000 0.990 0.00 0.00 1.00
#> 5th-C43_S121 3 0.0000 0.990 0.00 0.00 1.00
#> 5th-C45_S123 3 0.0000 0.990 0.00 0.00 1.00
#> 5th-C56_S95 3 0.0000 0.990 0.00 0.00 1.00
#> 5th-C58_S93 3 0.0000 0.990 0.00 0.00 1.00
#> 5th-C67_S105 3 0.0000 0.990 0.00 0.00 1.00
#> 5th-C6_S84 2 0.5706 0.528 0.00 0.68 0.32
#> 5th-C70_S103 3 0.1529 0.952 0.00 0.04 0.96
#> 5th-C73_S111 3 0.0000 0.990 0.00 0.00 1.00
#> 5th-C80_S116 1 0.0000 0.979 1.00 0.00 0.00
#> 5th-C81_S115 3 0.0000 0.990 0.00 0.00 1.00
#> 5th-C83_S111 3 0.4796 0.720 0.00 0.22 0.78
#> 5th-C87_S119 2 0.0000 0.992 0.00 1.00 0.00
#> 5th-C88_S117 3 0.0000 0.990 0.00 0.00 1.00
#> 6th-C15_S22 1 0.0000 0.979 1.00 0.00 0.00
#> 6th-C19_S35 1 0.0000 0.979 1.00 0.00 0.00
#> 6th-C1_S3 1 0.0000 0.979 1.00 0.00 0.00
#> 6th-C25_S43 1 0.0000 0.979 1.00 0.00 0.00
#> 6th-C28_S49 1 0.0000 0.979 1.00 0.00 0.00
#> 6th-C34_S61 2 0.0000 0.992 0.00 1.00 0.00
#> 6th-C45_S81 2 0.0000 0.992 0.00 1.00 0.00
#> 6th-C57_S17 1 0.0000 0.979 1.00 0.00 0.00
#> 6th-C58_S20 1 0.0000 0.979 1.00 0.00 0.00
#> 6th-C62_S25 1 0.0000 0.979 1.00 0.00 0.00
#> 6th-C64_S30 1 0.0000 0.979 1.00 0.00 0.00
#> 6th-C67_S36 1 0.0000 0.979 1.00 0.00 0.00
#> 6th-C82_S66 1 0.0000 0.979 1.00 0.00 0.00
#> 6th-C83_S65 2 0.0000 0.992 0.00 1.00 0.00
#> 6th-C84_S64 1 0.0000 0.979 1.00 0.00 0.00
#> 6th-C89_S77 1 0.0000 0.979 1.00 0.00 0.00
#> 6th-C90_S76 1 0.0000 0.979 1.00 0.00 0.00
#> 6th-C9_S12 2 0.0000 0.992 0.00 1.00 0.00
#> 7th-C12_S17 1 0.0000 0.979 1.00 0.00 0.00
#> 7th-C19_S36 1 0.0000 0.979 1.00 0.00 0.00
#> 7th-C1_S3 1 0.0000 0.979 1.00 0.00 0.00
#> 7th-C20_S35 1 0.0000 0.979 1.00 0.00 0.00
#> 7th-C21_S34 1 0.0000 0.979 1.00 0.00 0.00
#> 7th-C28_S48 1 0.0000 0.979 1.00 0.00 0.00
#> 7th-C2_S2 1 0.0000 0.979 1.00 0.00 0.00
#> 7th-C3_S1 1 0.0000 0.979 1.00 0.00 0.00
#> 7th-C47_S81 2 0.0000 0.992 0.00 1.00 0.00
#> 7th-C49_S4 2 0.0000 0.992 0.00 1.00 0.00
#> 7th-C4_S8 1 0.0000 0.979 1.00 0.00 0.00
#> 7th-C52_S9 1 0.0000 0.979 1.00 0.00 0.00
#> 7th-C57_S16 1 0.0000 0.979 1.00 0.00 0.00
#> 7th-C60_S22 1 0.0000 0.979 1.00 0.00 0.00
#> 7th-C65_S32 1 0.0000 0.979 1.00 0.00 0.00
#> 7th-C76_S52 3 0.0000 0.990 0.00 0.00 1.00
#> 7th-C81_S56 3 0.0000 0.990 0.00 0.00 1.00
#> 7th-C85_S69 2 0.0000 0.992 0.00 1.00 0.00
#> 7th-C94_S83 1 0.0000 0.979 1.00 0.00 0.00
#> 8th-C18_S110 2 0.0000 0.992 0.00 1.00 0.00
#> 8th-C21_S115 2 0.0000 0.992 0.00 1.00 0.00
#> 8th-C23_S121 2 0.0000 0.992 0.00 1.00 0.00
#> 8th-C26_S126 2 0.0000 0.992 0.00 1.00 0.00
#> 8th-C28_S131 2 0.0000 0.992 0.00 1.00 0.00
#> 8th-C37_S146 2 0.0000 0.992 0.00 1.00 0.00
#> 8th-C38_S147 1 0.0000 0.979 1.00 0.00 0.00
#> 8th-C47_S160 1 0.0000 0.979 1.00 0.00 0.00
#> 8th-C69_S119 2 0.0000 0.992 0.00 1.00 0.00
#> 8th-C70_S123 1 0.0000 0.979 1.00 0.00 0.00
#> 8th-C75_S128 1 0.0000 0.979 1.00 0.00 0.00
#> 8th-C79_S140 2 0.0000 0.992 0.00 1.00 0.00
#> 8th-C84_S143 1 0.0000 0.979 1.00 0.00 0.00
#> 8th-C90_S152 2 0.0000 0.992 0.00 1.00 0.00
#> 8th-C91_S158 2 0.0000 0.992 0.00 1.00 0.00
#> 8th-C94_S162 2 0.0000 0.992 0.00 1.00 0.00
#> 9th-C13_S24 1 0.0000 0.979 1.00 0.00 0.00
#> 9th-C14_S23 1 0.0000 0.979 1.00 0.00 0.00
#> 9th-C20_S35 2 0.0000 0.992 0.00 1.00 0.00
#> 9th-C22_S41 3 0.0000 0.990 0.00 0.00 1.00
#> 9th-C25_S45 1 0.0000 0.979 1.00 0.00 0.00
#> 9th-C2_S2 3 0.0000 0.990 0.00 0.00 1.00
#> 9th-C49_S4 1 0.0000 0.979 1.00 0.00 0.00
#> 9th-C51_S6 1 0.0000 0.979 1.00 0.00 0.00
#> 9th-C52_S10 2 0.0000 0.992 0.00 1.00 0.00
#> 9th-C59_S20 1 0.0000 0.979 1.00 0.00 0.00
#> 9th-C69_S39 1 0.0000 0.979 1.00 0.00 0.00
#> 9th-C75_S47 1 0.0000 0.979 1.00 0.00 0.00
#> 9th-C79_S57 1 0.5397 0.632 0.72 0.28 0.00
#> 9th-C85_S68 2 0.0000 0.992 0.00 1.00 0.00
#> 9th-C87_S66 2 0.0000 0.992 0.00 1.00 0.00
#> 9th-C88_S73 1 0.0000 0.979 1.00 0.00 0.00
#> 9th-C91_S78 1 0.0000 0.979 1.00 0.00 0.00
#> 9th-C92_S77 2 0.0000 0.992 0.00 1.00 0.00
#> 9th-C94_S83 1 0.0000 0.979 1.00 0.00 0.00
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> 10th_C11_S96 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 10th_C17_S97 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 10th_C28_S91 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 10th_C32_S56 1 0.0707 0.974 0.98 0.00 0.02 0.00
#> 10th_C33_S64 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 10th_C34_S92 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 10th_C37_S49 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 10th_C42_S109 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 10th_C43_S50 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 10th_C50_S73 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 10th_C51_S80 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 10th_C52_S110 4 0.3172 0.806 0.00 0.16 0.00 0.84
#> 10th_C53_S118 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 10th_C57_S81 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 10th_C58_S111 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 10th_C5_S95 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 10th_C61_S68 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 10th_C63_S82 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 10th_C64_S112 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 10th_C66_S126 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 10th_C6_S88 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 10th_C77_S120 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 10th_C78_S114 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 10th_C80_S77 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 10th_C86_S78 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 10th_C87_S71 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 10th_C95_S123 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 11th-C10_S63 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 11th-C12_S47 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 11th-C21_S4 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 11th-C22_S65 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 11th-C26_S12 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 11th-C27_S19 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 11th-C2_S8 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 11th-C30_S66 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 11th-C37_S6 2 0.1637 0.934 0.00 0.94 0.00 0.06
#> 11th-C43_S7 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 11th-C4_S62 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 11th-C54_S86 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 11th-C55_S24 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 11th-C56_S32 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 11th-C57_S40 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 11th-C62_S33 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 11th-C64_S72 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 11th-C67_S26 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 11th-C77_S82 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 11th-C93_S30 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 12th-C10_S155 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 12th-C15_S183 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 12th-C1_S195 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 12th-C21_S184 1 0.4713 0.440 0.64 0.36 0.00 0.00
#> 12th-C23_S149 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 12th-C35_S151 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 12th-C36_S158 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 12th-C37_S187 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 12th-C38_S194 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 12th-C39_S201 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 12th-C3_S181 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 12th-C40_S144 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 12th-C47_S153 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 12th-C4_S154 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 12th-C50_S210 4 0.4134 0.654 0.00 0.26 0.00 0.74
#> 12th-C53_S168 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 12th-C56_S211 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 12th-C57_S218 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 12th-C67_S205 1 0.2921 0.830 0.86 0.14 0.00 0.00
#> 12th-C71_S171 2 0.2921 0.839 0.00 0.86 0.00 0.14
#> 12th-C75_S206 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 12th-C8_S189 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 12th-C93_S209 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 13th_C15_S134 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 13th_C17_S186 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 13th_C18_S179 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 13th_C1_S147 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 13th_C20_S142 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 13th_C21_S135 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 13th_C27_S151 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 13th_C29_S188 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 13th_C31_S137 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 13th_C36_S196 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 13th_C38_S145 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 13th_C3_S132 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 13th_C46_S183 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 13th_C49_S155 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 13th_C4_S191 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 13th_C51_S170 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 13th_C52_S198 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 13th_C53_S205 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 13th_C54_S212 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 13th_C55_S156 2 0.1411 0.958 0.00 0.96 0.02 0.02
#> 13th_C57_S171 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 13th_C5_S184 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 13th_C63_S172 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 13th_C68_S165 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 13th_C69_S173 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 13th_C6_S177 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 13th_C70_S201 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 13th_C71_S208 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 13th_C72_S215 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 13th_C75_S159 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 13th_C77_S209 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 13th_C79_S174 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 13th_C80_S167 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 13th_C81_S160 1 0.1211 0.950 0.96 0.04 0.00 0.00
#> 13th_C86_S168 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 13th_C88_S218 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 13th_C89_S211 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 13th_C8_S140 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 13th_C92_S169 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 13th_C93_S162 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 1st-C13_S19 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 1st-C15_S3 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 1st-C18_S51 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 1st-C20_S12 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 1st-C39_S23 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 1st-C51_S41 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 1st-C53_S74 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 1st-C59_S77 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 1st-C62_S35 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 1st-C74_S37 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 1st-C79_S46 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 1st-C8_S10 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 1st-C96_S94 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 2nd-C19_S39 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 2nd-C1_S3 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 2nd-C27_S51 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 2nd-C28_S55 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 2nd-C2_S2 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 2nd-C36_S69 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 2nd-C37_S73 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 2nd-C3_S1 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 2nd-C49_S4 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 2nd-C4_S9 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 2nd-C51_S6 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 2nd-C52_S10 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 2nd-C58_S22 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 2nd-C5_S8 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 2nd-C69_S42 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 2nd-C7_S15 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 2nd-C87_S76 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 2nd-C94_S96 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 3rd-C23_S94 4 0.2921 0.830 0.00 0.14 0.00 0.86
#> 3rd-C25_S15 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 3rd-C32_S31 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 3rd-C3_S2 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 3rd-C44_S32 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 3rd-C51_S87 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 3rd-C52_S86 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 3rd-C56_S90 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 3rd-C60_S10 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 3rd-C61_S64 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 3rd-C63_S54 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 3rd-C69_S78 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 3rd-C7_S40 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 3rd-C85_S83 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 3rd-C96_S79 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 4th-C22_S45 4 0.2921 0.830 0.00 0.14 0.00 0.86
#> 4th-C27_S51 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 4th-C35_S68 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 4th-C37_S73 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 4th-C3_S1 4 0.4624 0.486 0.00 0.00 0.34 0.66
#> 4th-C45_S87 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 4th-C50_S5 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 4th-C57_S18 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 4th-C68_S41 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 4th-C93_S88 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 4th-C9_S13 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 5th-C10_S92 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 5th-C11_S91 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 5th-C14_S97 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 5th-C16_S98 3 0.1211 0.958 0.00 0.00 0.96 0.04
#> 5th-C18_S96 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 5th-C25_S108 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 5th-C40_S112 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 5th-C41_S113 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 5th-C42_S114 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 5th-C43_S121 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 5th-C45_S123 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 5th-C56_S95 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 5th-C58_S93 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 5th-C67_S105 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 5th-C6_S84 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 5th-C70_S103 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 5th-C73_S111 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 5th-C80_S116 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 5th-C81_S115 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 5th-C83_S111 2 0.3172 0.811 0.00 0.84 0.16 0.00
#> 5th-C87_S119 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 5th-C88_S117 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 6th-C15_S22 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 6th-C19_S35 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 6th-C1_S3 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 6th-C25_S43 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 6th-C28_S49 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 6th-C34_S61 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 6th-C45_S81 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 6th-C57_S17 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 6th-C58_S20 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 6th-C62_S25 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 6th-C64_S30 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 6th-C67_S36 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 6th-C82_S66 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 6th-C83_S65 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 6th-C84_S64 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 6th-C89_S77 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 6th-C90_S76 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 6th-C9_S12 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 7th-C12_S17 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 7th-C19_S36 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 7th-C1_S3 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 7th-C20_S35 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 7th-C21_S34 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 7th-C28_S48 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 7th-C2_S2 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 7th-C3_S1 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 7th-C47_S81 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 7th-C49_S4 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 7th-C4_S8 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 7th-C52_S9 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 7th-C57_S16 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 7th-C60_S22 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 7th-C65_S32 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 7th-C76_S52 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 7th-C81_S56 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 7th-C85_S69 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 7th-C94_S83 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 8th-C18_S110 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 8th-C21_S115 2 0.2345 0.889 0.00 0.90 0.00 0.10
#> 8th-C23_S121 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 8th-C26_S126 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 8th-C28_S131 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 8th-C37_S146 2 0.3400 0.782 0.00 0.82 0.00 0.18
#> 8th-C38_S147 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 8th-C47_S160 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 8th-C69_S119 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 8th-C70_S123 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 8th-C75_S128 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 8th-C79_S140 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 8th-C84_S143 1 0.0707 0.974 0.98 0.00 0.00 0.02
#> 8th-C90_S152 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 8th-C91_S158 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 8th-C94_S162 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 9th-C13_S24 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 9th-C14_S23 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 9th-C20_S35 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 9th-C22_S41 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 9th-C25_S45 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 9th-C2_S2 3 0.0000 0.999 0.00 0.00 1.00 0.00
#> 9th-C49_S4 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 9th-C51_S6 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 9th-C52_S10 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 9th-C59_S20 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 9th-C69_S39 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 9th-C75_S47 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 9th-C79_S57 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 9th-C85_S68 2 0.0707 0.973 0.00 0.98 0.00 0.02
#> 9th-C87_S66 2 0.0000 0.991 0.00 1.00 0.00 0.00
#> 9th-C88_S73 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 9th-C91_S78 1 0.0000 0.993 1.00 0.00 0.00 0.00
#> 9th-C92_S77 4 0.0000 0.977 0.00 0.00 0.00 1.00
#> 9th-C94_S83 1 0.0000 0.993 1.00 0.00 0.00 0.00
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
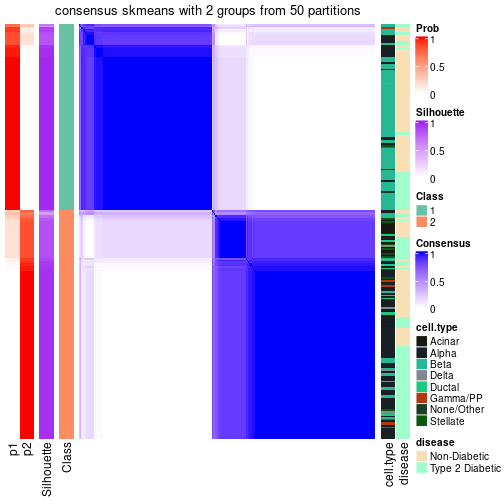
consensus_heatmap(res, k = 3)
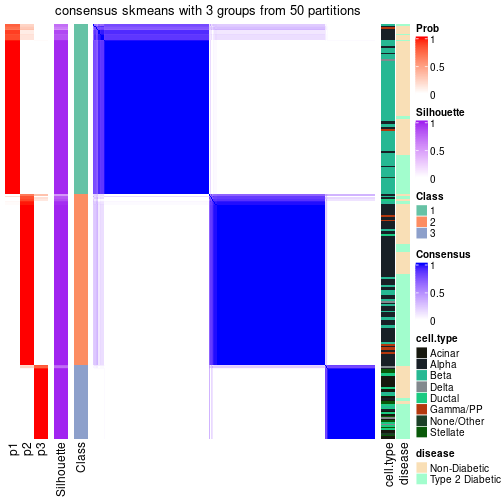
consensus_heatmap(res, k = 4)
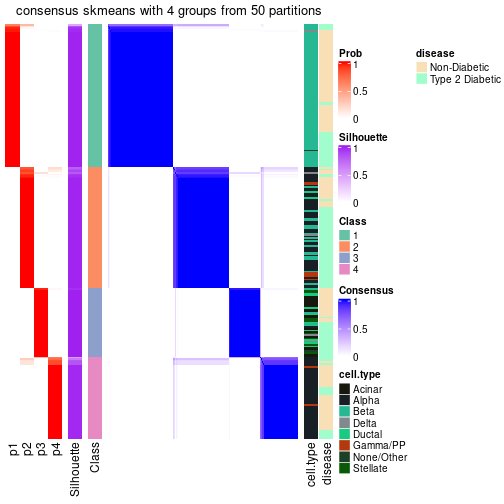
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
membership_heatmap(res, k = 3)
membership_heatmap(res, k = 4)
As soon as the classes for columns are determined, the signatures that are significantly different between subgroups can be looked for. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
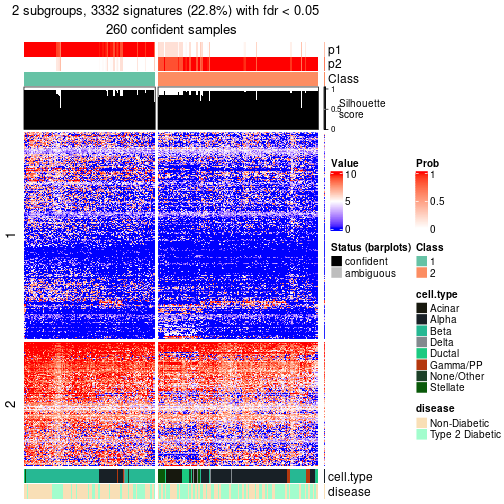
get_signatures(res, k = 3, scale_rows = FALSE)

get_signatures(res, k = 4, scale_rows = FALSE)
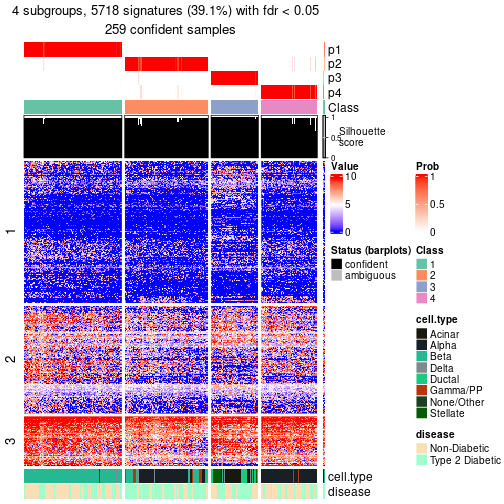
Compare the overlap of signatures from different k:
compare_signatures(res)
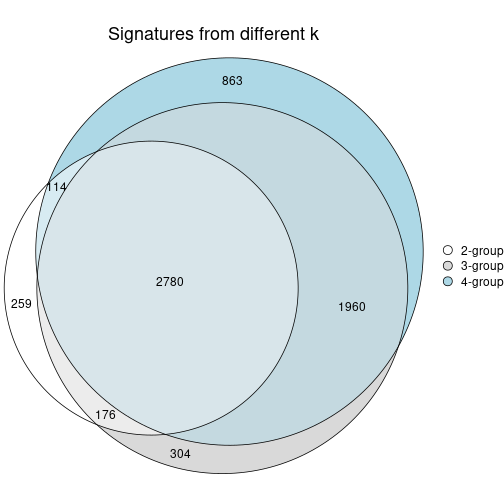
get_signature() returns a data frame invisibly. To get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows (which is done by automatically selecting number of clusters).If there are too many signatures, top_signatures = ... can be set to only show the
signatures with the highest FDRs:
# code only for demonstration
# e.g. to show the top 500 most significant rows
tb = get_signature(res, k = ..., top_signatures = 500)
If the signatures are defined as these which are uniquely high in current group, diff_method argument
can be set to "uniquely_high_in_one_group":
# code only for demonstration
tb = get_signature(res, k = ..., diff_method = "uniquely_high_in_one_group")
UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
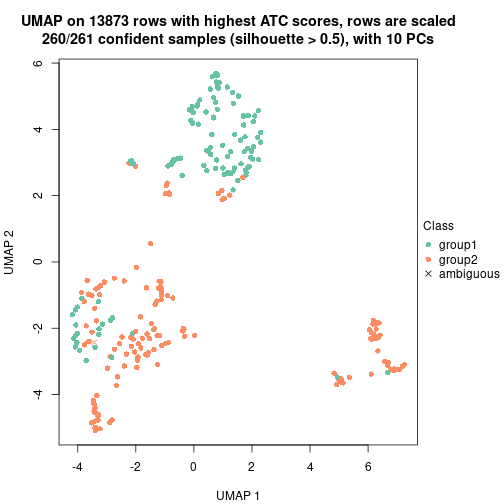
dimension_reduction(res, k = 3, method = "UMAP")
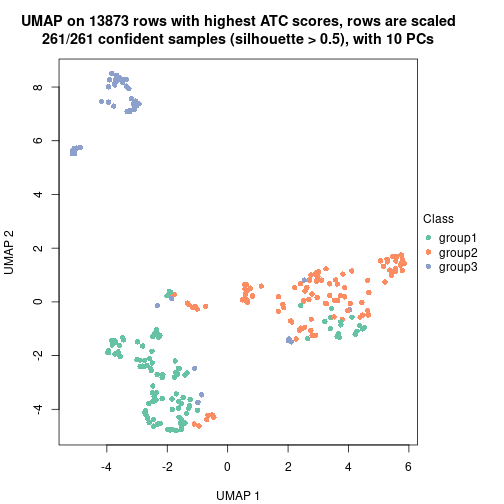
dimension_reduction(res, k = 4, method = "UMAP")
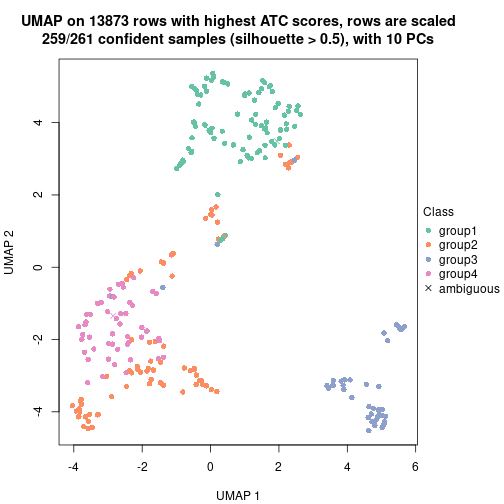
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
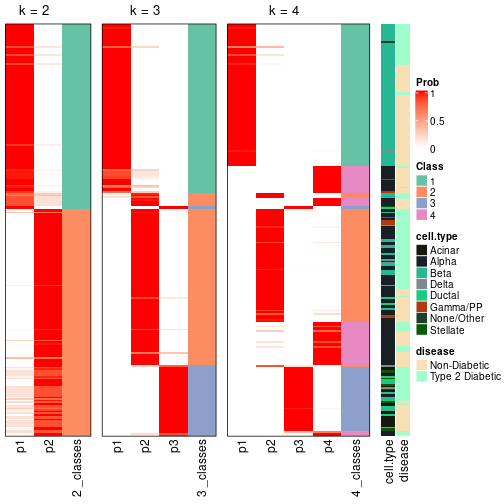
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n_sample cell.type(p-value) disease(p-value) k
#> ATC:skmeans 260 1.19e-22 6.17e-07 2
#> ATC:skmeans 261 6.80e-57 3.01e-06 3
#> ATC:skmeans 259 6.20e-72 2.69e-08 4
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
Parent node: Node02. Child nodes: Node0111 , Node0112 , Node0113 , Node0121-leaf , Node0122 , Node0123 , Node0124-leaf , Node0211-leaf , Node0212-leaf , Node0221-leaf , Node0222-leaf , Node0231-leaf , Node0232-leaf , Node0233-leaf .
The object with results only for a single top-value method and a single partitioning method can be extracted as:
res = res_rh["021"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4.
#> On a matrix with 13804 rows and 90 columns.
#> Top rows (1290) are extracted by 'ATC' method.
#> Subgroups are detected by 'skmeans' method.
#> Performed in total 150 partitions by row resampling.
#> Best k for subgroups seems to be 2.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_partitions"
#> [7] "compare_signatures" "consensus_heatmap" "dimension_reduction"
#> [10] "functional_enrichment" "get_anno_col" "get_anno"
#> [13] "get_classes" "get_consensus" "get_matrix"
#> [16] "get_membership" "get_param" "get_signatures"
#> [19] "get_stats" "is_best_k" "is_stable_k"
#> [22] "membership_heatmap" "ncol" "nrow"
#> [25] "plot_ecdf" "predict_classes" "rownames"
#> [28] "select_partition_number" "show" "suggest_best_k"
#> [31] "test_to_known_factors" "top_rows_heatmap"
collect_plots() function collects all the plots made from res for all k (number of subgroups)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
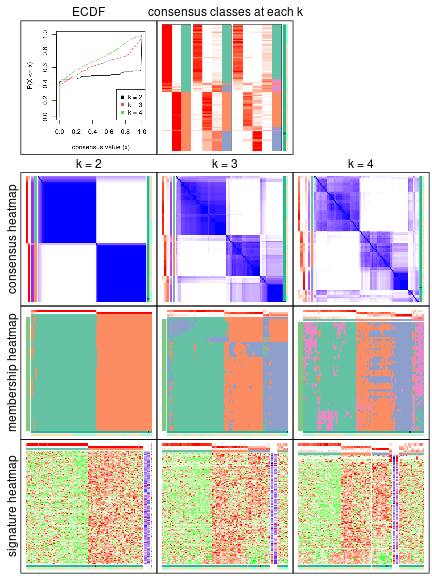
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, higher 1-PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
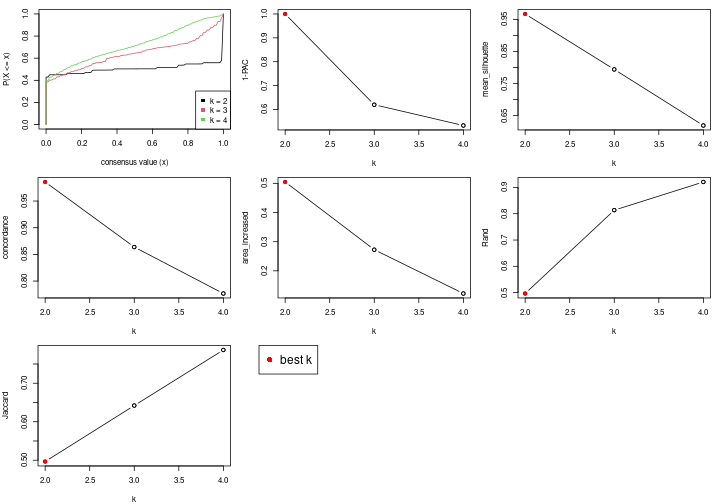
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 1.000 0.967 0.986 0.505 0.497 0.497
#> 3 3 0.620 0.794 0.864 0.272 0.813 0.642
#> 4 4 0.532 0.619 0.777 0.122 0.921 0.786
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 2
Following is the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall subgroup
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> 10th_C11_S96 1 0.000 0.978 1.00 0.00
#> 10th_C17_S97 1 0.000 0.978 1.00 0.00
#> 10th_C32_S56 1 0.000 0.978 1.00 0.00
#> 10th_C33_S64 1 0.000 0.978 1.00 0.00
#> 10th_C37_S49 1 0.000 0.978 1.00 0.00
#> 10th_C61_S68 1 0.000 0.978 1.00 0.00
#> 10th_C64_S112 1 0.000 0.978 1.00 0.00
#> 10th_C66_S126 1 0.000 0.978 1.00 0.00
#> 11th-C21_S4 2 0.000 0.993 0.00 1.00
#> 11th-C22_S65 1 0.827 0.659 0.74 0.26
#> 11th-C27_S19 2 0.000 0.993 0.00 1.00
#> 11th-C54_S86 2 0.000 0.993 0.00 1.00
#> 12th-C10_S155 1 0.000 0.978 1.00 0.00
#> 12th-C15_S183 1 0.000 0.978 1.00 0.00
#> 12th-C21_S184 1 0.000 0.978 1.00 0.00
#> 12th-C35_S151 1 0.000 0.978 1.00 0.00
#> 12th-C38_S194 1 0.000 0.978 1.00 0.00
#> 12th-C3_S181 1 0.000 0.978 1.00 0.00
#> 12th-C47_S153 1 0.000 0.978 1.00 0.00
#> 12th-C67_S205 2 0.000 0.993 0.00 1.00
#> 12th-C93_S209 2 0.000 0.993 0.00 1.00
#> 13th_C15_S134 2 0.000 0.993 0.00 1.00
#> 13th_C57_S171 1 0.000 0.978 1.00 0.00
#> 13th_C75_S159 1 0.000 0.978 1.00 0.00
#> 13th_C80_S167 2 0.000 0.993 0.00 1.00
#> 13th_C81_S160 2 0.000 0.993 0.00 1.00
#> 1st-C13_S19 2 0.000 0.993 0.00 1.00
#> 1st-C39_S23 2 0.000 0.993 0.00 1.00
#> 1st-C79_S46 2 0.000 0.993 0.00 1.00
#> 1st-C96_S94 1 0.141 0.961 0.98 0.02
#> 2nd-C19_S39 2 0.000 0.993 0.00 1.00
#> 2nd-C27_S51 2 0.000 0.993 0.00 1.00
#> 2nd-C37_S73 1 0.000 0.978 1.00 0.00
#> 2nd-C49_S4 1 0.000 0.978 1.00 0.00
#> 2nd-C51_S6 2 0.000 0.993 0.00 1.00
#> 2nd-C52_S10 2 0.000 0.993 0.00 1.00
#> 2nd-C5_S8 2 0.000 0.993 0.00 1.00
#> 2nd-C7_S15 2 0.000 0.993 0.00 1.00
#> 2nd-C87_S76 1 0.958 0.399 0.62 0.38
#> 3rd-C25_S15 2 0.000 0.993 0.00 1.00
#> 3rd-C56_S90 2 0.000 0.993 0.00 1.00
#> 3rd-C60_S10 1 0.529 0.858 0.88 0.12
#> 3rd-C96_S79 2 0.000 0.993 0.00 1.00
#> 4th-C45_S87 2 0.000 0.993 0.00 1.00
#> 4th-C93_S88 2 0.000 0.993 0.00 1.00
#> 5th-C14_S97 1 0.000 0.978 1.00 0.00
#> 5th-C18_S96 1 0.000 0.978 1.00 0.00
#> 5th-C80_S116 2 0.000 0.993 0.00 1.00
#> 6th-C15_S22 1 0.000 0.978 1.00 0.00
#> 6th-C19_S35 2 0.000 0.993 0.00 1.00
#> 6th-C1_S3 1 0.000 0.978 1.00 0.00
#> 6th-C25_S43 2 0.000 0.993 0.00 1.00
#> 6th-C28_S49 2 0.000 0.993 0.00 1.00
#> 6th-C57_S17 1 0.000 0.978 1.00 0.00
#> 6th-C58_S20 1 0.000 0.978 1.00 0.00
#> 6th-C62_S25 2 0.000 0.993 0.00 1.00
#> 6th-C64_S30 1 0.000 0.978 1.00 0.00
#> 6th-C67_S36 2 0.000 0.993 0.00 1.00
#> 6th-C82_S66 1 0.000 0.978 1.00 0.00
#> 6th-C84_S64 1 0.000 0.978 1.00 0.00
#> 6th-C89_S77 2 0.000 0.993 0.00 1.00
#> 6th-C90_S76 1 0.000 0.978 1.00 0.00
#> 7th-C12_S17 2 0.000 0.993 0.00 1.00
#> 7th-C19_S36 1 0.000 0.978 1.00 0.00
#> 7th-C1_S3 1 0.000 0.978 1.00 0.00
#> 7th-C20_S35 2 0.141 0.973 0.02 0.98
#> 7th-C21_S34 1 0.000 0.978 1.00 0.00
#> 7th-C28_S48 2 0.000 0.993 0.00 1.00
#> 7th-C2_S2 2 0.000 0.993 0.00 1.00
#> 7th-C3_S1 2 0.000 0.993 0.00 1.00
#> 7th-C4_S8 2 0.000 0.993 0.00 1.00
#> 7th-C52_S9 2 0.000 0.993 0.00 1.00
#> 7th-C57_S16 2 0.000 0.993 0.00 1.00
#> 7th-C60_S22 2 0.000 0.993 0.00 1.00
#> 7th-C65_S32 1 0.000 0.978 1.00 0.00
#> 7th-C94_S83 1 0.000 0.978 1.00 0.00
#> 8th-C38_S147 1 0.000 0.978 1.00 0.00
#> 8th-C47_S160 1 0.000 0.978 1.00 0.00
#> 8th-C70_S123 1 0.000 0.978 1.00 0.00
#> 8th-C75_S128 1 0.000 0.978 1.00 0.00
#> 8th-C84_S143 1 0.760 0.725 0.78 0.22
#> 9th-C13_S24 1 0.000 0.978 1.00 0.00
#> 9th-C14_S23 1 0.000 0.978 1.00 0.00
#> 9th-C25_S45 1 0.000 0.978 1.00 0.00
#> 9th-C51_S6 1 0.000 0.978 1.00 0.00
#> 9th-C59_S20 2 0.000 0.993 0.00 1.00
#> 9th-C69_S39 2 0.000 0.993 0.00 1.00
#> 9th-C88_S73 1 0.000 0.978 1.00 0.00
#> 9th-C91_S78 2 0.000 0.993 0.00 1.00
#> 9th-C94_S83 2 0.827 0.640 0.26 0.74
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> 10th_C11_S96 1 0.2066 0.887 0.94 0.00 0.06
#> 10th_C17_S97 1 0.0000 0.904 1.00 0.00 0.00
#> 10th_C32_S56 1 0.4291 0.837 0.82 0.00 0.18
#> 10th_C33_S64 1 0.3340 0.876 0.88 0.00 0.12
#> 10th_C37_S49 1 0.0892 0.903 0.98 0.00 0.02
#> 10th_C61_S68 1 0.6192 0.473 0.58 0.00 0.42
#> 10th_C64_S112 3 0.5397 0.384 0.28 0.00 0.72
#> 10th_C66_S126 1 0.0000 0.904 1.00 0.00 0.00
#> 11th-C21_S4 3 0.5835 0.818 0.00 0.34 0.66
#> 11th-C22_S65 3 0.5416 0.654 0.08 0.10 0.82
#> 11th-C27_S19 2 0.5560 0.397 0.00 0.70 0.30
#> 11th-C54_S86 3 0.5835 0.818 0.00 0.34 0.66
#> 12th-C10_S155 1 0.7029 0.390 0.54 0.02 0.44
#> 12th-C15_S183 1 0.0892 0.901 0.98 0.00 0.02
#> 12th-C21_S184 1 0.2959 0.885 0.90 0.00 0.10
#> 12th-C35_S151 1 0.3340 0.876 0.88 0.00 0.12
#> 12th-C38_S194 1 0.2959 0.885 0.90 0.00 0.10
#> 12th-C3_S181 1 0.0000 0.904 1.00 0.00 0.00
#> 12th-C47_S153 1 0.4002 0.852 0.84 0.00 0.16
#> 12th-C67_S205 3 0.5835 0.818 0.00 0.34 0.66
#> 12th-C93_S209 2 0.2537 0.844 0.00 0.92 0.08
#> 13th_C15_S134 3 0.5835 0.818 0.00 0.34 0.66
#> 13th_C57_S171 1 0.0000 0.904 1.00 0.00 0.00
#> 13th_C75_S159 3 0.6045 0.101 0.38 0.00 0.62
#> 13th_C80_S167 3 0.5835 0.818 0.00 0.34 0.66
#> 13th_C81_S160 3 0.5835 0.818 0.00 0.34 0.66
#> 1st-C13_S19 3 0.6309 0.501 0.00 0.50 0.50
#> 1st-C39_S23 2 0.3340 0.832 0.00 0.88 0.12
#> 1st-C79_S46 2 0.2537 0.772 0.00 0.92 0.08
#> 1st-C96_S94 1 0.8853 0.475 0.54 0.14 0.32
#> 2nd-C19_S39 3 0.6045 0.764 0.00 0.38 0.62
#> 2nd-C27_S51 2 0.2959 0.840 0.00 0.90 0.10
#> 2nd-C37_S73 1 0.2959 0.885 0.90 0.00 0.10
#> 2nd-C49_S4 1 0.3340 0.876 0.88 0.00 0.12
#> 2nd-C51_S6 2 0.0892 0.849 0.00 0.98 0.02
#> 2nd-C52_S10 2 0.3340 0.708 0.00 0.88 0.12
#> 2nd-C5_S8 2 0.0000 0.846 0.00 1.00 0.00
#> 2nd-C7_S15 2 0.2066 0.848 0.00 0.94 0.06
#> 2nd-C87_S76 3 0.7398 0.588 0.18 0.12 0.70
#> 3rd-C25_S15 2 0.0000 0.846 0.00 1.00 0.00
#> 3rd-C56_S90 2 0.0892 0.849 0.00 0.98 0.02
#> 3rd-C60_S10 2 0.8631 0.532 0.22 0.60 0.18
#> 3rd-C96_S79 3 0.5835 0.818 0.00 0.34 0.66
#> 4th-C45_S87 2 0.4002 0.806 0.00 0.84 0.16
#> 4th-C93_S88 2 0.0892 0.834 0.00 0.98 0.02
#> 5th-C14_S97 1 0.0892 0.901 0.98 0.00 0.02
#> 5th-C18_S96 1 0.0892 0.901 0.98 0.00 0.02
#> 5th-C80_S116 2 0.0892 0.834 0.00 0.98 0.02
#> 6th-C15_S22 1 0.1529 0.897 0.96 0.00 0.04
#> 6th-C19_S35 3 0.5835 0.818 0.00 0.34 0.66
#> 6th-C1_S3 1 0.3340 0.855 0.88 0.00 0.12
#> 6th-C25_S43 3 0.5835 0.818 0.00 0.34 0.66
#> 6th-C28_S49 2 0.0000 0.846 0.00 1.00 0.00
#> 6th-C57_S17 1 0.1529 0.897 0.96 0.00 0.04
#> 6th-C58_S20 1 0.0892 0.901 0.98 0.00 0.02
#> 6th-C62_S25 2 0.0000 0.846 0.00 1.00 0.00
#> 6th-C64_S30 1 0.1529 0.900 0.96 0.00 0.04
#> 6th-C67_S36 3 0.5835 0.818 0.00 0.34 0.66
#> 6th-C82_S66 1 0.1529 0.897 0.96 0.00 0.04
#> 6th-C84_S64 1 0.9083 0.263 0.54 0.28 0.18
#> 6th-C89_S77 2 0.3340 0.820 0.00 0.88 0.12
#> 6th-C90_S76 1 0.2537 0.892 0.92 0.00 0.08
#> 7th-C12_S17 2 0.0000 0.846 0.00 1.00 0.00
#> 7th-C19_S36 1 0.1529 0.897 0.96 0.00 0.04
#> 7th-C1_S3 1 0.1529 0.897 0.96 0.00 0.04
#> 7th-C20_S35 2 0.7058 0.684 0.10 0.72 0.18
#> 7th-C21_S34 1 0.1529 0.897 0.96 0.00 0.04
#> 7th-C28_S48 2 0.0000 0.846 0.00 1.00 0.00
#> 7th-C2_S2 2 0.3340 0.836 0.00 0.88 0.12
#> 7th-C3_S1 2 0.7058 0.684 0.10 0.72 0.18
#> 7th-C4_S8 2 0.3340 0.832 0.00 0.88 0.12
#> 7th-C52_S9 2 0.3340 0.831 0.00 0.88 0.12
#> 7th-C57_S16 2 0.1529 0.844 0.00 0.96 0.04
#> 7th-C60_S22 2 0.3686 0.819 0.00 0.86 0.14
#> 7th-C65_S32 1 0.1529 0.897 0.96 0.00 0.04
#> 7th-C94_S83 1 0.1529 0.897 0.96 0.00 0.04
#> 8th-C38_S147 1 0.1529 0.901 0.96 0.00 0.04
#> 8th-C47_S160 1 0.2066 0.896 0.94 0.00 0.06
#> 8th-C70_S123 1 0.0000 0.904 1.00 0.00 0.00
#> 8th-C75_S128 1 0.0000 0.904 1.00 0.00 0.00
#> 8th-C84_S143 3 0.5012 0.651 0.08 0.08 0.84
#> 9th-C13_S24 1 0.3340 0.876 0.88 0.00 0.12
#> 9th-C14_S23 1 0.3686 0.865 0.86 0.00 0.14
#> 9th-C25_S45 1 0.4002 0.852 0.84 0.00 0.16
#> 9th-C51_S6 1 0.2959 0.886 0.90 0.00 0.10
#> 9th-C59_S20 3 0.5835 0.818 0.00 0.34 0.66
#> 9th-C69_S39 2 0.2537 0.774 0.00 0.92 0.08
#> 9th-C88_S73 1 0.1529 0.897 0.96 0.00 0.04
#> 9th-C91_S78 3 0.5835 0.818 0.00 0.34 0.66
#> 9th-C94_S83 2 0.9147 0.455 0.20 0.54 0.26
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> 10th_C11_S96 1 0.5489 0.6108 0.70 0.06 0.00 0.24
#> 10th_C17_S97 1 0.0707 0.7463 0.98 0.00 0.00 0.02
#> 10th_C32_S56 4 0.4855 0.1764 0.40 0.00 0.00 0.60
#> 10th_C33_S64 1 0.4277 0.5769 0.72 0.00 0.00 0.28
#> 10th_C37_S49 1 0.2647 0.7200 0.88 0.00 0.00 0.12
#> 10th_C61_S68 4 0.5106 0.4988 0.24 0.00 0.04 0.72
#> 10th_C64_S112 4 0.6104 0.5833 0.18 0.00 0.14 0.68
#> 10th_C66_S126 1 0.0707 0.7446 0.98 0.00 0.00 0.02
#> 11th-C21_S4 3 0.0707 0.8479 0.00 0.00 0.98 0.02
#> 11th-C22_S65 4 0.6766 0.4549 0.10 0.00 0.38 0.52
#> 11th-C27_S19 3 0.6988 -0.1664 0.00 0.38 0.50 0.12
#> 11th-C54_S86 3 0.0000 0.8674 0.00 0.00 1.00 0.00
#> 12th-C10_S155 1 0.7677 0.1506 0.56 0.04 0.12 0.28
#> 12th-C15_S183 1 0.1211 0.7450 0.96 0.00 0.00 0.04
#> 12th-C21_S184 1 0.4522 0.5327 0.68 0.00 0.00 0.32
#> 12th-C35_S151 1 0.4522 0.5389 0.68 0.00 0.00 0.32
#> 12th-C38_S194 1 0.4277 0.5861 0.72 0.00 0.00 0.28
#> 12th-C3_S181 1 0.0000 0.7464 1.00 0.00 0.00 0.00
#> 12th-C47_S153 1 0.4713 0.4624 0.64 0.00 0.00 0.36
#> 12th-C67_S205 3 0.0000 0.8674 0.00 0.00 1.00 0.00
#> 12th-C93_S209 2 0.5636 0.6317 0.00 0.68 0.26 0.06
#> 13th_C15_S134 3 0.0707 0.8599 0.00 0.02 0.98 0.00
#> 13th_C57_S171 1 0.0000 0.7464 1.00 0.00 0.00 0.00
#> 13th_C75_S159 4 0.6216 0.5485 0.22 0.00 0.12 0.66
#> 13th_C80_S167 3 0.0000 0.8674 0.00 0.00 1.00 0.00
#> 13th_C81_S160 3 0.0000 0.8674 0.00 0.00 1.00 0.00
#> 1st-C13_S19 3 0.6797 0.4413 0.00 0.24 0.60 0.16
#> 1st-C39_S23 2 0.4949 0.7417 0.00 0.76 0.18 0.06
#> 1st-C79_S46 2 0.5000 0.3412 0.00 0.50 0.50 0.00
#> 1st-C96_S94 4 0.9032 0.2735 0.30 0.12 0.14 0.44
#> 2nd-C19_S39 3 0.3935 0.7532 0.00 0.10 0.84 0.06
#> 2nd-C27_S51 2 0.2830 0.6980 0.00 0.90 0.06 0.04
#> 2nd-C37_S73 1 0.2921 0.7139 0.86 0.00 0.00 0.14
#> 2nd-C49_S4 1 0.4406 0.5560 0.70 0.00 0.00 0.30
#> 2nd-C51_S6 2 0.4079 0.7535 0.00 0.80 0.18 0.02
#> 2nd-C52_S10 3 0.4907 -0.1299 0.00 0.42 0.58 0.00
#> 2nd-C5_S8 2 0.3610 0.7501 0.00 0.80 0.20 0.00
#> 2nd-C7_S15 2 0.5915 0.5810 0.00 0.56 0.40 0.04
#> 2nd-C87_S76 4 0.8306 0.3921 0.10 0.08 0.34 0.48
#> 3rd-C25_S15 2 0.4624 0.6663 0.00 0.66 0.34 0.00
#> 3rd-C56_S90 2 0.4277 0.7194 0.00 0.72 0.28 0.00
#> 3rd-C60_S10 2 0.7095 0.0923 0.18 0.56 0.00 0.26
#> 3rd-C96_S79 3 0.0000 0.8674 0.00 0.00 1.00 0.00
#> 4th-C45_S87 2 0.2335 0.6863 0.00 0.92 0.02 0.06
#> 4th-C93_S88 2 0.4855 0.5914 0.00 0.60 0.40 0.00
#> 5th-C14_S97 1 0.1211 0.7450 0.96 0.00 0.00 0.04
#> 5th-C18_S96 1 0.2647 0.7244 0.88 0.00 0.00 0.12
#> 5th-C80_S116 2 0.4948 0.5206 0.00 0.56 0.44 0.00
#> 6th-C15_S22 1 0.3400 0.6844 0.82 0.00 0.00 0.18
#> 6th-C19_S35 3 0.0707 0.8599 0.00 0.02 0.98 0.00
#> 6th-C1_S3 1 0.4731 0.6641 0.78 0.06 0.00 0.16
#> 6th-C25_S43 3 0.0000 0.8674 0.00 0.00 1.00 0.00
#> 6th-C28_S49 2 0.4277 0.7172 0.00 0.72 0.28 0.00
#> 6th-C57_S17 1 0.2647 0.7212 0.88 0.00 0.00 0.12
#> 6th-C58_S20 1 0.3975 0.7007 0.76 0.00 0.00 0.24
#> 6th-C62_S25 2 0.3801 0.7472 0.00 0.78 0.22 0.00
#> 6th-C64_S30 1 0.4277 0.6479 0.72 0.00 0.00 0.28
#> 6th-C67_S36 3 0.0707 0.8599 0.00 0.02 0.98 0.00
#> 6th-C82_S66 1 0.3400 0.6844 0.82 0.00 0.00 0.18
#> 6th-C84_S64 1 0.7738 0.0921 0.44 0.26 0.00 0.30
#> 6th-C89_S77 2 0.5077 0.6560 0.00 0.76 0.16 0.08
#> 6th-C90_S76 1 0.3610 0.7119 0.80 0.00 0.00 0.20
#> 7th-C12_S17 2 0.3975 0.7393 0.00 0.76 0.24 0.00
#> 7th-C19_S36 1 0.3801 0.6506 0.78 0.00 0.00 0.22
#> 7th-C1_S3 1 0.3172 0.6989 0.84 0.00 0.00 0.16
#> 7th-C20_S35 2 0.3400 0.5766 0.00 0.82 0.00 0.18
#> 7th-C21_S34 1 0.2647 0.7212 0.88 0.00 0.00 0.12
#> 7th-C28_S48 2 0.4134 0.7291 0.00 0.74 0.26 0.00
#> 7th-C2_S2 2 0.4079 0.7330 0.00 0.80 0.18 0.02
#> 7th-C3_S1 2 0.4905 0.6545 0.02 0.80 0.06 0.12
#> 7th-C4_S8 2 0.2706 0.7302 0.00 0.90 0.08 0.02
#> 7th-C52_S9 2 0.2921 0.7506 0.00 0.86 0.14 0.00
#> 7th-C57_S16 2 0.3975 0.7424 0.00 0.76 0.24 0.00
#> 7th-C60_S22 2 0.1211 0.6813 0.00 0.96 0.00 0.04
#> 7th-C65_S32 1 0.2345 0.7301 0.90 0.00 0.00 0.10
#> 7th-C94_S83 1 0.4553 0.7162 0.78 0.04 0.00 0.18
#> 8th-C38_S147 1 0.2345 0.7271 0.90 0.00 0.00 0.10
#> 8th-C47_S160 1 0.2921 0.7075 0.86 0.00 0.00 0.14
#> 8th-C70_S123 1 0.2647 0.7357 0.88 0.00 0.00 0.12
#> 8th-C75_S128 1 0.0000 0.7464 1.00 0.00 0.00 0.00
#> 8th-C84_S143 4 0.5594 0.2929 0.02 0.00 0.46 0.52
#> 9th-C13_S24 1 0.3172 0.7010 0.84 0.00 0.00 0.16
#> 9th-C14_S23 1 0.4907 0.3390 0.58 0.00 0.00 0.42
#> 9th-C25_S45 1 0.4948 0.2717 0.56 0.00 0.00 0.44
#> 9th-C51_S6 1 0.4624 0.4564 0.66 0.00 0.00 0.34
#> 9th-C59_S20 3 0.0707 0.8495 0.00 0.00 0.98 0.02
#> 9th-C69_S39 2 0.5000 0.3818 0.00 0.50 0.50 0.00
#> 9th-C88_S73 1 0.2647 0.7220 0.88 0.00 0.00 0.12
#> 9th-C91_S78 3 0.0000 0.8674 0.00 0.00 1.00 0.00
#> 9th-C94_S83 4 0.9034 0.1568 0.16 0.32 0.10 0.42
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
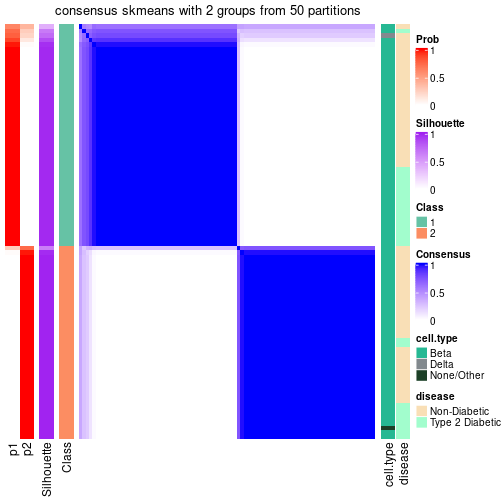
consensus_heatmap(res, k = 3)
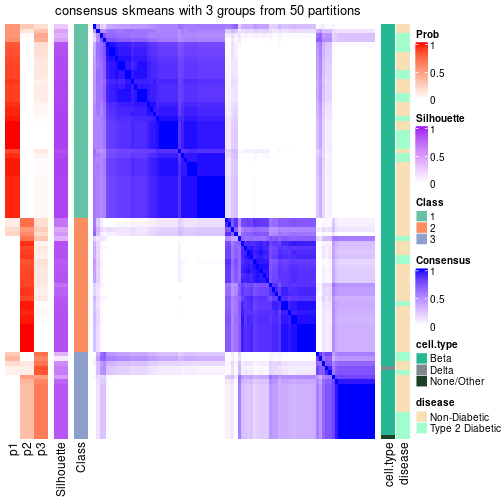
consensus_heatmap(res, k = 4)
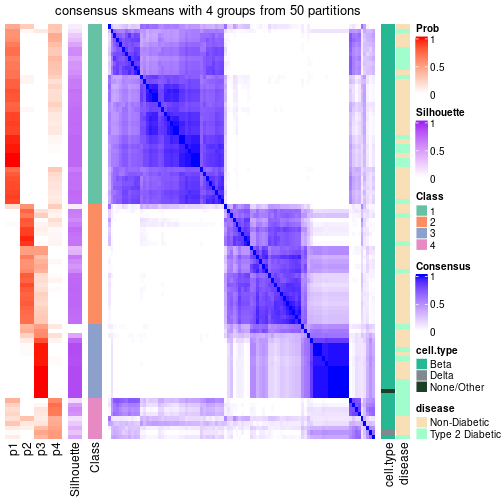
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
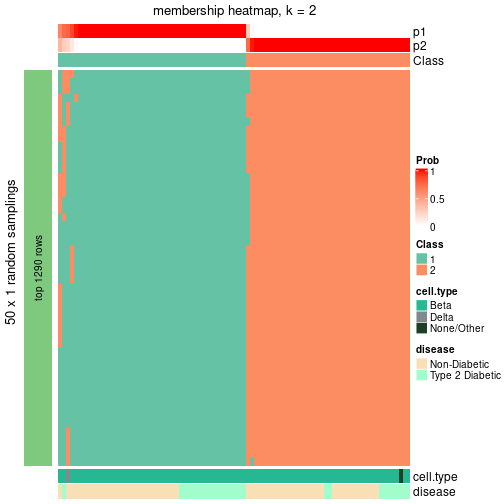
membership_heatmap(res, k = 3)
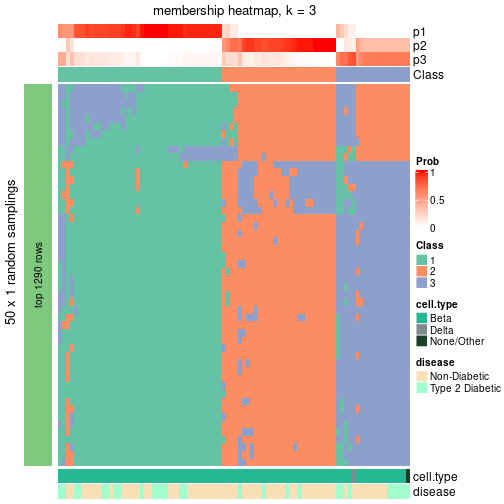
membership_heatmap(res, k = 4)
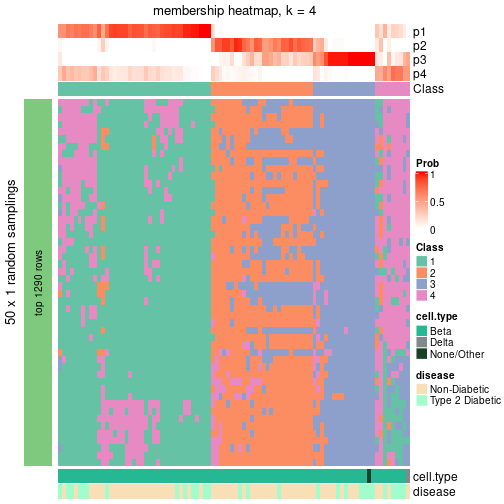
As soon as the classes for columns are determined, the signatures that are significantly different between subgroups can be looked for. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
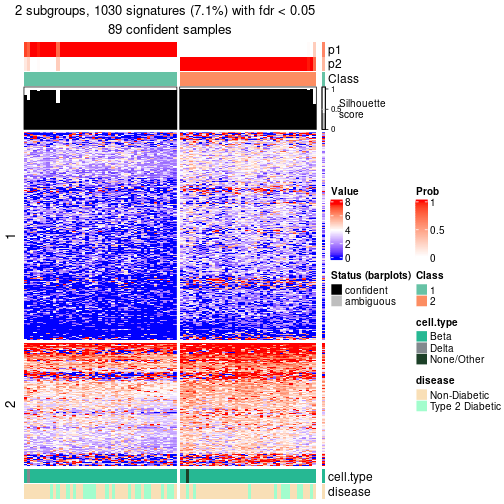
get_signatures(res, k = 3, scale_rows = FALSE)
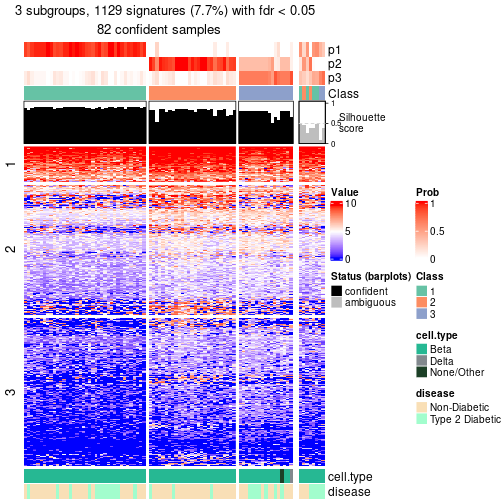
get_signatures(res, k = 4, scale_rows = FALSE)
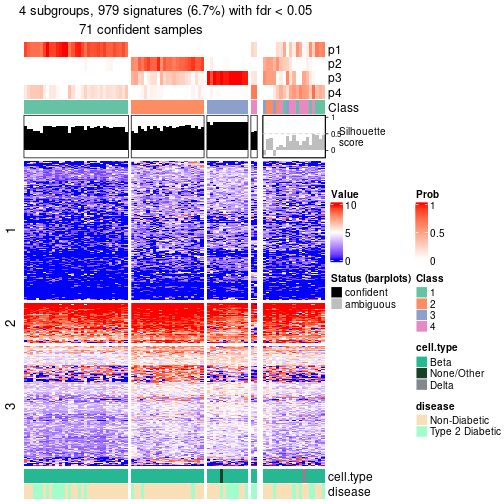
Compare the overlap of signatures from different k:
compare_signatures(res)
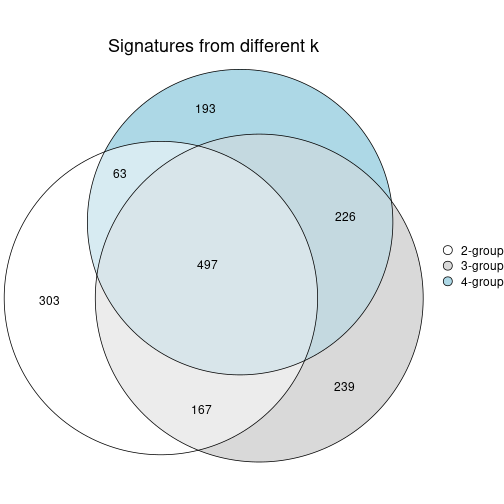
get_signature() returns a data frame invisibly. To get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows (which is done by automatically selecting number of clusters).If there are too many signatures, top_signatures = ... can be set to only show the
signatures with the highest FDRs:
# code only for demonstration
# e.g. to show the top 500 most significant rows
tb = get_signature(res, k = ..., top_signatures = 500)
If the signatures are defined as these which are uniquely high in current group, diff_method argument
can be set to "uniquely_high_in_one_group":
# code only for demonstration
tb = get_signature(res, k = ..., diff_method = "uniquely_high_in_one_group")
UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")

dimension_reduction(res, k = 3, method = "UMAP")
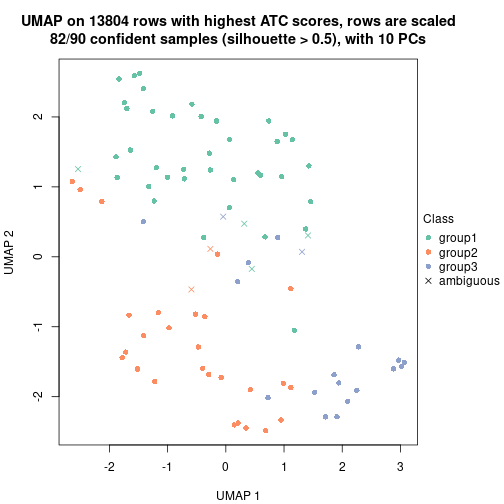
dimension_reduction(res, k = 4, method = "UMAP")
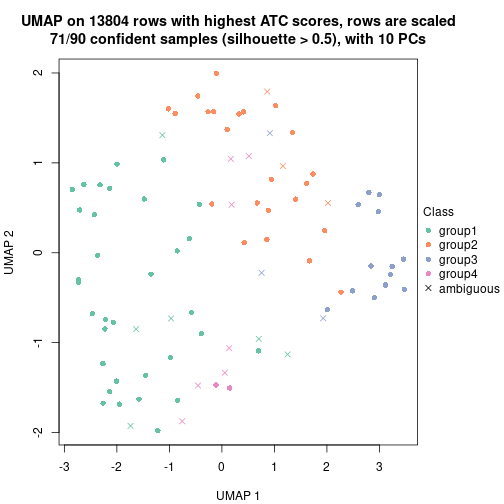
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
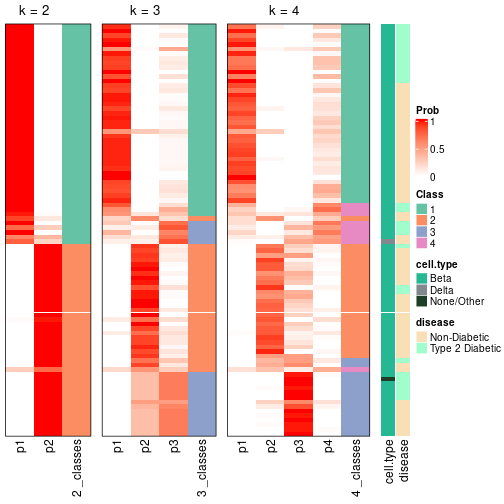
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n_sample cell.type(p-value) disease(p-value) k
#> ATC:skmeans 89 0.3655 0.2147 2
#> ATC:skmeans 82 0.0977 0.0497 3
#> ATC:skmeans 71 0.2100 0.0244 4
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
Parent node: Node02. Child nodes: Node0111 , Node0112 , Node0113 , Node0121-leaf , Node0122 , Node0123 , Node0124-leaf , Node0211-leaf , Node0212-leaf , Node0221-leaf , Node0222-leaf , Node0231-leaf , Node0232-leaf , Node0233-leaf .
The object with results only for a single top-value method and a single partitioning method can be extracted as:
res = res_rh["022"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4.
#> On a matrix with 13810 rows and 76 columns.
#> Top rows (1381) are extracted by 'ATC' method.
#> Subgroups are detected by 'skmeans' method.
#> Performed in total 150 partitions by row resampling.
#> Best k for subgroups seems to be 2.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_partitions"
#> [7] "compare_signatures" "consensus_heatmap" "dimension_reduction"
#> [10] "functional_enrichment" "get_anno_col" "get_anno"
#> [13] "get_classes" "get_consensus" "get_matrix"
#> [16] "get_membership" "get_param" "get_signatures"
#> [19] "get_stats" "is_best_k" "is_stable_k"
#> [22] "membership_heatmap" "ncol" "nrow"
#> [25] "plot_ecdf" "predict_classes" "rownames"
#> [28] "select_partition_number" "show" "suggest_best_k"
#> [31] "test_to_known_factors" "top_rows_heatmap"
collect_plots() function collects all the plots made from res for all k (number of subgroups)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
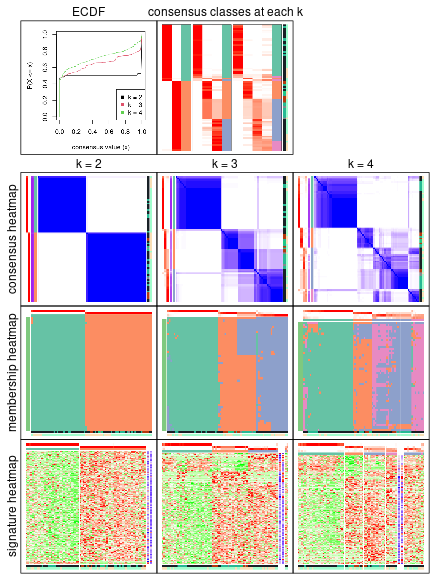
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, higher 1-PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
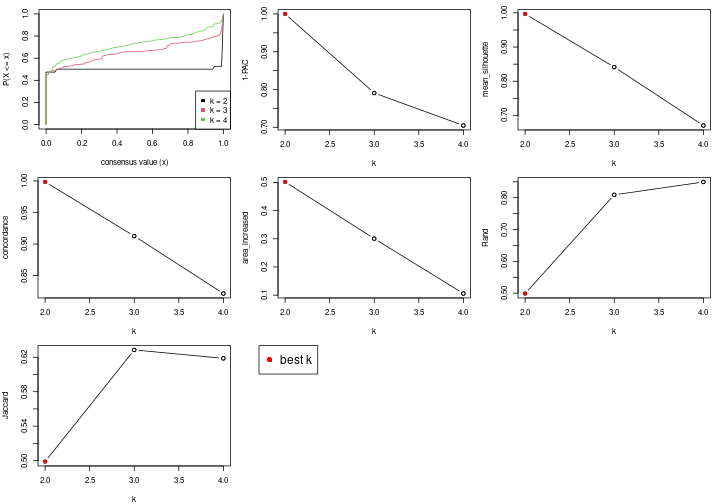
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 1.000 0.997 0.998 0.502 0.499 0.499
#> 3 3 0.791 0.841 0.913 0.300 0.809 0.628
#> 4 4 0.705 0.671 0.822 0.106 0.849 0.619
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 2
Following is the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall subgroup
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> 10th_C28_S91 2 0.000 0.999 0.00 1.00
#> 10th_C43_S50 1 0.000 0.998 1.00 0.00
#> 10th_C51_S80 1 0.000 0.998 1.00 0.00
#> 10th_C53_S118 1 0.000 0.998 1.00 0.00
#> 10th_C57_S81 2 0.000 0.999 0.00 1.00
#> 10th_C58_S111 2 0.000 0.999 0.00 1.00
#> 10th_C5_S95 1 0.000 0.998 1.00 0.00
#> 10th_C6_S88 2 0.000 0.999 0.00 1.00
#> 10th_C78_S114 2 0.000 0.999 0.00 1.00
#> 11th-C10_S63 2 0.000 0.999 0.00 1.00
#> 11th-C30_S66 2 0.000 0.999 0.00 1.00
#> 11th-C37_S6 1 0.000 0.998 1.00 0.00
#> 11th-C62_S33 2 0.000 0.999 0.00 1.00
#> 11th-C67_S26 1 0.000 0.998 1.00 0.00
#> 11th-C93_S30 2 0.000 0.999 0.00 1.00
#> 12th-C1_S195 1 0.000 0.998 1.00 0.00
#> 12th-C23_S149 1 0.000 0.998 1.00 0.00
#> 12th-C37_S187 2 0.000 0.999 0.00 1.00
#> 12th-C39_S201 1 0.000 0.998 1.00 0.00
#> 12th-C40_S144 1 0.000 0.998 1.00 0.00
#> 12th-C4_S154 1 0.000 0.998 1.00 0.00
#> 12th-C71_S171 1 0.000 0.998 1.00 0.00
#> 12th-C75_S206 1 0.000 0.998 1.00 0.00
#> 12th-C8_S189 1 0.000 0.998 1.00 0.00
#> 13th_C17_S186 2 0.000 0.999 0.00 1.00
#> 13th_C18_S179 2 0.000 0.999 0.00 1.00
#> 13th_C1_S147 1 0.000 0.998 1.00 0.00
#> 13th_C20_S142 1 0.000 0.998 1.00 0.00
#> 13th_C21_S135 2 0.000 0.999 0.00 1.00
#> 13th_C29_S188 1 0.000 0.998 1.00 0.00
#> 13th_C31_S137 2 0.000 0.999 0.00 1.00
#> 13th_C38_S145 1 0.000 0.998 1.00 0.00
#> 13th_C3_S132 1 0.000 0.998 1.00 0.00
#> 13th_C46_S183 1 0.000 0.998 1.00 0.00
#> 13th_C4_S191 1 0.000 0.998 1.00 0.00
#> 13th_C51_S170 2 0.000 0.999 0.00 1.00
#> 13th_C52_S198 2 0.000 0.999 0.00 1.00
#> 13th_C53_S205 1 0.327 0.936 0.94 0.06
#> 13th_C54_S212 1 0.000 0.998 1.00 0.00
#> 13th_C55_S156 2 0.000 0.999 0.00 1.00
#> 13th_C5_S184 2 0.000 0.999 0.00 1.00
#> 13th_C63_S172 2 0.000 0.999 0.00 1.00
#> 13th_C68_S165 2 0.000 0.999 0.00 1.00
#> 13th_C69_S173 2 0.000 0.999 0.00 1.00
#> 13th_C6_S177 1 0.000 0.998 1.00 0.00
#> 13th_C70_S201 2 0.000 0.999 0.00 1.00
#> 13th_C71_S208 2 0.000 0.999 0.00 1.00
#> 13th_C77_S209 1 0.000 0.998 1.00 0.00
#> 13th_C79_S174 2 0.000 0.999 0.00 1.00
#> 13th_C86_S168 1 0.000 0.998 1.00 0.00
#> 13th_C88_S218 2 0.000 0.999 0.00 1.00
#> 13th_C89_S211 2 0.000 0.999 0.00 1.00
#> 13th_C92_S169 1 0.000 0.998 1.00 0.00
#> 13th_C93_S162 1 0.000 0.998 1.00 0.00
#> 1st-C15_S3 2 0.000 0.999 0.00 1.00
#> 2nd-C1_S3 2 0.000 0.999 0.00 1.00
#> 2nd-C69_S42 2 0.000 0.999 0.00 1.00
#> 2nd-C94_S96 2 0.000 0.999 0.00 1.00
#> 4th-C68_S41 2 0.000 0.999 0.00 1.00
#> 5th-C41_S113 2 0.000 0.999 0.00 1.00
#> 5th-C83_S111 2 0.000 0.999 0.00 1.00
#> 6th-C34_S61 1 0.000 0.998 1.00 0.00
#> 6th-C45_S81 1 0.000 0.998 1.00 0.00
#> 6th-C9_S12 1 0.000 0.998 1.00 0.00
#> 7th-C47_S81 2 0.000 0.999 0.00 1.00
#> 7th-C49_S4 2 0.000 0.999 0.00 1.00
#> 7th-C85_S69 1 0.000 0.998 1.00 0.00
#> 8th-C18_S110 2 0.000 0.999 0.00 1.00
#> 8th-C21_S115 2 0.000 0.999 0.00 1.00
#> 8th-C26_S126 1 0.000 0.998 1.00 0.00
#> 8th-C37_S146 2 0.327 0.936 0.06 0.94
#> 8th-C69_S119 2 0.000 0.999 0.00 1.00
#> 8th-C91_S158 2 0.000 0.999 0.00 1.00
#> 9th-C20_S35 2 0.000 0.999 0.00 1.00
#> 9th-C85_S68 2 0.000 0.999 0.00 1.00
#> 9th-C87_S66 1 0.000 0.998 1.00 0.00
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> 10th_C28_S91 3 0.2537 0.856 0.00 0.08 0.92
#> 10th_C43_S50 1 0.0892 0.970 0.98 0.00 0.02
#> 10th_C51_S80 1 0.0000 0.984 1.00 0.00 0.00
#> 10th_C53_S118 1 0.0000 0.984 1.00 0.00 0.00
#> 10th_C57_S81 3 0.0000 0.886 0.00 0.00 1.00
#> 10th_C58_S111 2 0.0892 0.748 0.00 0.98 0.02
#> 10th_C5_S95 1 0.0000 0.984 1.00 0.00 0.00
#> 10th_C6_S88 2 0.5835 0.682 0.00 0.66 0.34
#> 10th_C78_S114 2 0.5835 0.682 0.00 0.66 0.34
#> 11th-C10_S63 2 0.0000 0.745 0.00 1.00 0.00
#> 11th-C30_S66 2 0.0000 0.745 0.00 1.00 0.00
#> 11th-C37_S6 1 0.0000 0.984 1.00 0.00 0.00
#> 11th-C62_S33 2 0.2066 0.714 0.00 0.94 0.06
#> 11th-C67_S26 3 0.5643 0.584 0.22 0.02 0.76
#> 11th-C93_S30 3 0.0892 0.876 0.00 0.02 0.98
#> 12th-C1_S195 1 0.0000 0.984 1.00 0.00 0.00
#> 12th-C23_S149 1 0.0000 0.984 1.00 0.00 0.00
#> 12th-C37_S187 3 0.4002 0.782 0.00 0.16 0.84
#> 12th-C39_S201 1 0.0000 0.984 1.00 0.00 0.00
#> 12th-C40_S144 1 0.0000 0.984 1.00 0.00 0.00
#> 12th-C4_S154 1 0.0892 0.970 0.98 0.02 0.00
#> 12th-C71_S171 1 0.0000 0.984 1.00 0.00 0.00
#> 12th-C75_S206 1 0.0000 0.984 1.00 0.00 0.00
#> 12th-C8_S189 1 0.0000 0.984 1.00 0.00 0.00
#> 13th_C17_S186 2 0.5706 0.711 0.00 0.68 0.32
#> 13th_C18_S179 3 0.0000 0.886 0.00 0.00 1.00
#> 13th_C1_S147 1 0.0000 0.984 1.00 0.00 0.00
#> 13th_C20_S142 1 0.0000 0.984 1.00 0.00 0.00
#> 13th_C21_S135 2 0.5706 0.711 0.00 0.68 0.32
#> 13th_C29_S188 1 0.0000 0.984 1.00 0.00 0.00
#> 13th_C31_S137 3 0.2537 0.856 0.00 0.08 0.92
#> 13th_C38_S145 1 0.0000 0.984 1.00 0.00 0.00
#> 13th_C3_S132 1 0.0000 0.984 1.00 0.00 0.00
#> 13th_C46_S183 1 0.0892 0.970 0.98 0.02 0.00
#> 13th_C4_S191 1 0.0000 0.984 1.00 0.00 0.00
#> 13th_C51_S170 2 0.5706 0.711 0.00 0.68 0.32
#> 13th_C52_S198 2 0.0000 0.745 0.00 1.00 0.00
#> 13th_C53_S205 2 0.8483 0.307 0.26 0.60 0.14
#> 13th_C54_S212 1 0.0000 0.984 1.00 0.00 0.00
#> 13th_C55_S156 3 0.5835 0.322 0.00 0.34 0.66
#> 13th_C5_S184 2 0.5706 0.711 0.00 0.68 0.32
#> 13th_C63_S172 2 0.5706 0.711 0.00 0.68 0.32
#> 13th_C68_S165 2 0.5706 0.711 0.00 0.68 0.32
#> 13th_C69_S173 3 0.5016 0.612 0.00 0.24 0.76
#> 13th_C6_S177 1 0.0000 0.984 1.00 0.00 0.00
#> 13th_C70_S201 2 0.5706 0.711 0.00 0.68 0.32
#> 13th_C71_S208 2 0.5706 0.711 0.00 0.68 0.32
#> 13th_C77_S209 1 0.0000 0.984 1.00 0.00 0.00
#> 13th_C79_S174 3 0.2066 0.867 0.00 0.06 0.94
#> 13th_C86_S168 1 0.0000 0.984 1.00 0.00 0.00
#> 13th_C88_S218 3 0.2537 0.856 0.00 0.08 0.92
#> 13th_C89_S211 2 0.5706 0.711 0.00 0.68 0.32
#> 13th_C92_S169 1 0.0000 0.984 1.00 0.00 0.00
#> 13th_C93_S162 1 0.0000 0.984 1.00 0.00 0.00
#> 1st-C15_S3 3 0.0000 0.886 0.00 0.00 1.00
#> 2nd-C1_S3 3 0.2959 0.805 0.00 0.10 0.90
#> 2nd-C69_S42 3 0.2959 0.837 0.00 0.10 0.90
#> 2nd-C94_S96 3 0.0000 0.886 0.00 0.00 1.00
#> 4th-C68_S41 2 0.4002 0.620 0.00 0.84 0.16
#> 5th-C41_S113 2 0.0000 0.745 0.00 1.00 0.00
#> 5th-C83_S111 2 0.5706 0.711 0.00 0.68 0.32
#> 6th-C34_S61 1 0.6927 0.634 0.70 0.06 0.24
#> 6th-C45_S81 1 0.0892 0.970 0.98 0.02 0.00
#> 6th-C9_S12 1 0.1529 0.953 0.96 0.00 0.04
#> 7th-C47_S81 2 0.0000 0.745 0.00 1.00 0.00
#> 7th-C49_S4 3 0.0000 0.886 0.00 0.00 1.00
#> 7th-C85_S69 1 0.0000 0.984 1.00 0.00 0.00
#> 8th-C18_S110 2 0.0000 0.745 0.00 1.00 0.00
#> 8th-C21_S115 3 0.0000 0.886 0.00 0.00 1.00
#> 8th-C26_S126 1 0.0000 0.984 1.00 0.00 0.00
#> 8th-C37_S146 3 0.0000 0.886 0.00 0.00 1.00
#> 8th-C69_S119 2 0.0000 0.745 0.00 1.00 0.00
#> 8th-C91_S158 2 0.0892 0.748 0.00 0.98 0.02
#> 9th-C20_S35 3 0.2066 0.847 0.00 0.06 0.94
#> 9th-C85_S68 3 0.0000 0.886 0.00 0.00 1.00
#> 9th-C87_S66 1 0.3832 0.879 0.88 0.02 0.10
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> 10th_C28_S91 3 0.1913 0.3956 0.00 0.02 0.94 0.04
#> 10th_C43_S50 1 0.3801 0.7633 0.78 0.00 0.00 0.22
#> 10th_C51_S80 1 0.2345 0.8890 0.90 0.00 0.00 0.10
#> 10th_C53_S118 1 0.0000 0.9368 1.00 0.00 0.00 0.00
#> 10th_C57_S81 3 0.4624 -0.4785 0.00 0.00 0.66 0.34
#> 10th_C58_S111 2 0.3935 0.7662 0.00 0.84 0.10 0.06
#> 10th_C5_S95 1 0.1637 0.9033 0.94 0.00 0.00 0.06
#> 10th_C6_S88 3 0.7148 0.5774 0.00 0.22 0.56 0.22
#> 10th_C78_S114 3 0.6840 0.5877 0.00 0.18 0.60 0.22
#> 11th-C10_S63 2 0.1913 0.8817 0.00 0.94 0.04 0.02
#> 11th-C30_S66 2 0.2345 0.8608 0.00 0.90 0.00 0.10
#> 11th-C37_S6 1 0.0707 0.9279 0.98 0.00 0.00 0.02
#> 11th-C62_S33 2 0.1637 0.8665 0.00 0.94 0.06 0.00
#> 11th-C67_S26 4 0.6159 0.7291 0.04 0.02 0.30 0.64
#> 11th-C93_S30 4 0.4977 0.7938 0.00 0.00 0.46 0.54
#> 12th-C1_S195 1 0.0000 0.9368 1.00 0.00 0.00 0.00
#> 12th-C23_S149 1 0.0000 0.9368 1.00 0.00 0.00 0.00
#> 12th-C37_S187 3 0.6921 0.3408 0.00 0.26 0.58 0.16
#> 12th-C39_S201 1 0.0000 0.9368 1.00 0.00 0.00 0.00
#> 12th-C40_S144 1 0.2345 0.8890 0.90 0.00 0.00 0.10
#> 12th-C4_S154 1 0.3935 0.8411 0.84 0.06 0.00 0.10
#> 12th-C71_S171 1 0.0000 0.9368 1.00 0.00 0.00 0.00
#> 12th-C75_S206 1 0.0000 0.9368 1.00 0.00 0.00 0.00
#> 12th-C8_S189 1 0.2345 0.8890 0.90 0.00 0.00 0.10
#> 13th_C17_S186 3 0.7346 0.5913 0.00 0.20 0.52 0.28
#> 13th_C18_S179 3 0.2921 0.0548 0.00 0.00 0.86 0.14
#> 13th_C1_S147 1 0.0000 0.9368 1.00 0.00 0.00 0.00
#> 13th_C20_S142 1 0.0000 0.9368 1.00 0.00 0.00 0.00
#> 13th_C21_S135 3 0.7346 0.5913 0.00 0.20 0.52 0.28
#> 13th_C29_S188 1 0.0000 0.9368 1.00 0.00 0.00 0.00
#> 13th_C31_S137 3 0.1211 0.3065 0.00 0.00 0.96 0.04
#> 13th_C38_S145 1 0.1637 0.9107 0.94 0.00 0.00 0.06
#> 13th_C3_S132 1 0.0707 0.9279 0.98 0.00 0.00 0.02
#> 13th_C46_S183 1 0.4088 0.8226 0.82 0.04 0.00 0.14
#> 13th_C4_S191 1 0.0000 0.9368 1.00 0.00 0.00 0.00
#> 13th_C51_S170 3 0.7474 0.5752 0.00 0.22 0.50 0.28
#> 13th_C52_S198 2 0.1211 0.8930 0.00 0.96 0.00 0.04
#> 13th_C53_S205 2 0.4211 0.7728 0.04 0.84 0.02 0.10
#> 13th_C54_S212 1 0.0000 0.9368 1.00 0.00 0.00 0.00
#> 13th_C55_S156 3 0.3853 0.5223 0.00 0.16 0.82 0.02
#> 13th_C5_S184 3 0.7346 0.5913 0.00 0.20 0.52 0.28
#> 13th_C63_S172 3 0.7346 0.5913 0.00 0.20 0.52 0.28
#> 13th_C68_S165 3 0.7346 0.5913 0.00 0.20 0.52 0.28
#> 13th_C69_S173 3 0.5902 0.5920 0.00 0.16 0.70 0.14
#> 13th_C6_S177 1 0.0000 0.9368 1.00 0.00 0.00 0.00
#> 13th_C70_S201 3 0.7346 0.5913 0.00 0.20 0.52 0.28
#> 13th_C71_S208 3 0.7346 0.5913 0.00 0.20 0.52 0.28
#> 13th_C77_S209 1 0.0000 0.9368 1.00 0.00 0.00 0.00
#> 13th_C79_S174 3 0.0707 0.3411 0.00 0.00 0.98 0.02
#> 13th_C86_S168 1 0.0000 0.9368 1.00 0.00 0.00 0.00
#> 13th_C88_S218 3 0.1211 0.3704 0.00 0.00 0.96 0.04
#> 13th_C89_S211 3 0.7285 0.5904 0.00 0.18 0.52 0.30
#> 13th_C92_S169 1 0.0000 0.9368 1.00 0.00 0.00 0.00
#> 13th_C93_S162 1 0.0000 0.9368 1.00 0.00 0.00 0.00
#> 1st-C15_S3 4 0.4994 0.7845 0.00 0.00 0.48 0.52
#> 2nd-C1_S3 4 0.6843 0.6997 0.00 0.10 0.44 0.46
#> 2nd-C69_S42 3 0.3247 0.4671 0.00 0.06 0.88 0.06
#> 2nd-C94_S96 4 0.4994 0.7827 0.00 0.00 0.48 0.52
#> 4th-C68_S41 2 0.2706 0.8265 0.00 0.90 0.08 0.02
#> 5th-C41_S113 2 0.0000 0.8946 0.00 1.00 0.00 0.00
#> 5th-C83_S111 3 0.7427 0.5730 0.00 0.20 0.50 0.30
#> 6th-C34_S61 4 0.8073 0.2132 0.36 0.10 0.06 0.48
#> 6th-C45_S81 1 0.1913 0.9078 0.94 0.04 0.00 0.02
#> 6th-C9_S12 1 0.5820 0.5510 0.68 0.00 0.08 0.24
#> 7th-C47_S81 2 0.0000 0.8946 0.00 1.00 0.00 0.00
#> 7th-C49_S4 4 0.4855 0.7905 0.00 0.00 0.40 0.60
#> 7th-C85_S69 1 0.0000 0.9368 1.00 0.00 0.00 0.00
#> 8th-C18_S110 2 0.1637 0.8871 0.00 0.94 0.00 0.06
#> 8th-C21_S115 3 0.4948 -0.7291 0.00 0.00 0.56 0.44
#> 8th-C26_S126 1 0.0000 0.9368 1.00 0.00 0.00 0.00
#> 8th-C37_S146 4 0.4948 0.7983 0.00 0.00 0.44 0.56
#> 8th-C69_S119 2 0.0707 0.8954 0.00 0.98 0.00 0.02
#> 8th-C91_S158 2 0.4610 0.7860 0.00 0.80 0.10 0.10
#> 9th-C20_S35 3 0.6840 -0.3160 0.00 0.18 0.60 0.22
#> 9th-C85_S68 3 0.4994 -0.7516 0.00 0.00 0.52 0.48
#> 9th-C87_S66 1 0.8165 -0.0894 0.44 0.08 0.08 0.40
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)

consensus_heatmap(res, k = 3)
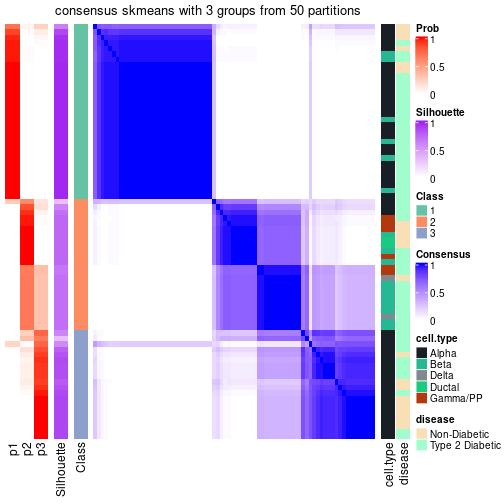
consensus_heatmap(res, k = 4)
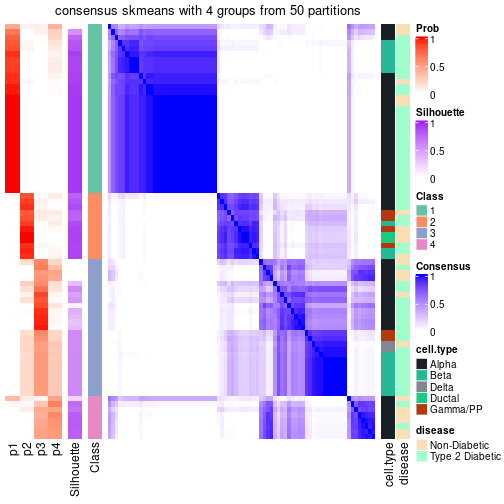
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
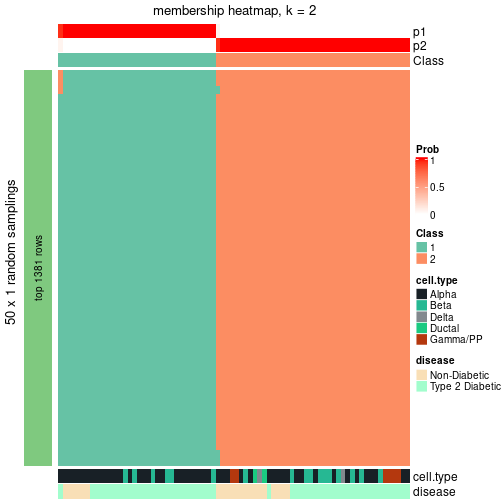
membership_heatmap(res, k = 3)
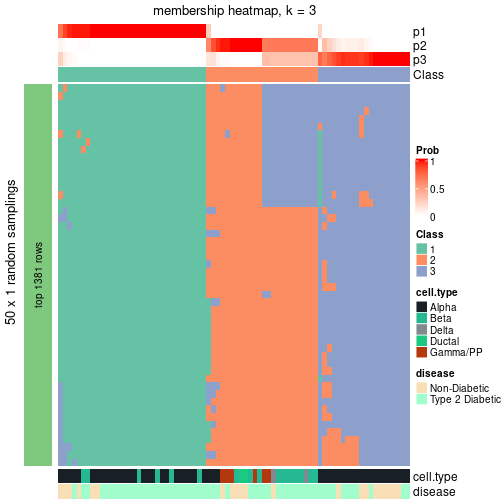
membership_heatmap(res, k = 4)
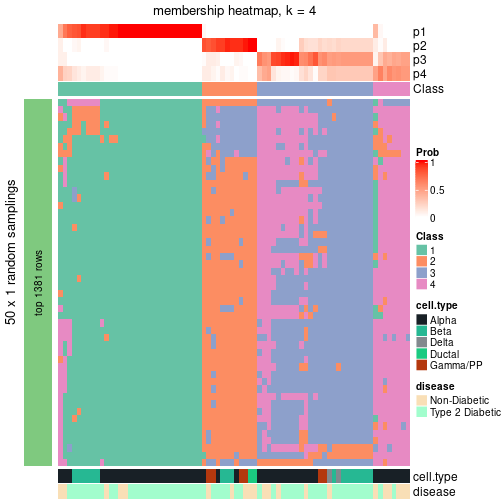
As soon as the classes for columns are determined, the signatures that are significantly different between subgroups can be looked for. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
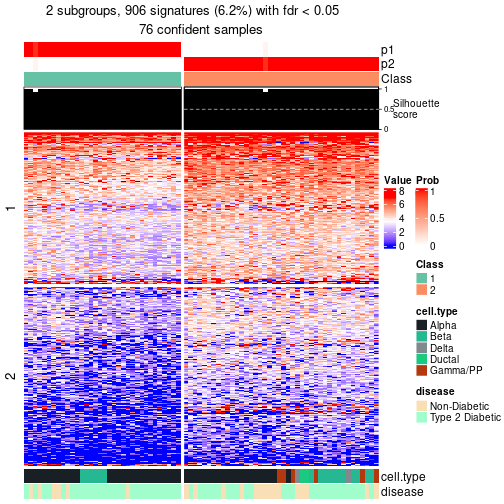
get_signatures(res, k = 3, scale_rows = FALSE)
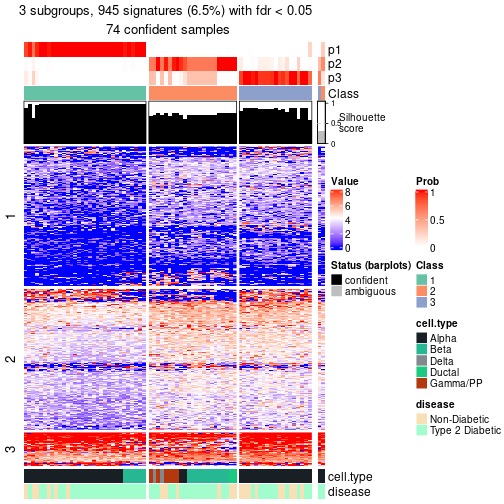
get_signatures(res, k = 4, scale_rows = FALSE)
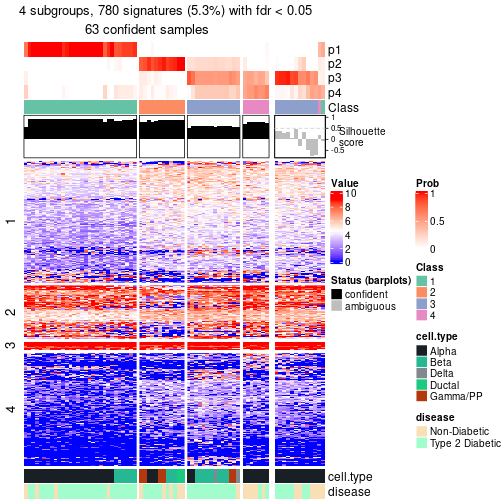
Compare the overlap of signatures from different k:
compare_signatures(res)
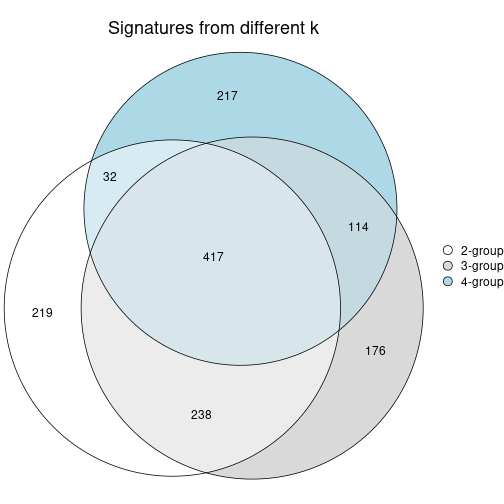
get_signature() returns a data frame invisibly. To get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows (which is done by automatically selecting number of clusters).If there are too many signatures, top_signatures = ... can be set to only show the
signatures with the highest FDRs:
# code only for demonstration
# e.g. to show the top 500 most significant rows
tb = get_signature(res, k = ..., top_signatures = 500)
If the signatures are defined as these which are uniquely high in current group, diff_method argument
can be set to "uniquely_high_in_one_group":
# code only for demonstration
tb = get_signature(res, k = ..., diff_method = "uniquely_high_in_one_group")
UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
dimension_reduction(res, k = 3, method = "UMAP")
dimension_reduction(res, k = 4, method = "UMAP")
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
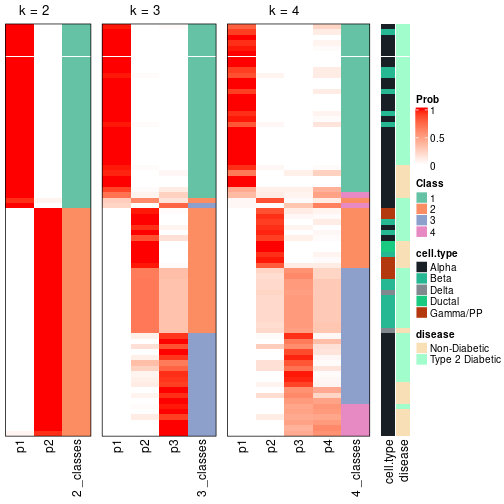
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n_sample cell.type(p-value) disease(p-value) k
#> ATC:skmeans 76 1.92e-02 0.13533 2
#> ATC:skmeans 74 5.28e-08 0.08672 3
#> ATC:skmeans 63 9.05e-06 0.00198 4
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
Parent node: Node02. Child nodes: Node0111 , Node0112 , Node0113 , Node0121-leaf , Node0122 , Node0123 , Node0124-leaf , Node0211-leaf , Node0212-leaf , Node0221-leaf , Node0222-leaf , Node0231-leaf , Node0232-leaf , Node0233-leaf .
The object with results only for a single top-value method and a single partitioning method can be extracted as:
res = res_rh["023"]
A summary of res and all the functions that can be applied to it:
res
#> A 'ConsensusPartition' object with k = 2, 3, 4.
#> On a matrix with 13549 rows and 43 columns.
#> Top rows (1355) are extracted by 'ATC' method.
#> Subgroups are detected by 'skmeans' method.
#> Performed in total 150 partitions by row resampling.
#> Best k for subgroups seems to be 3.
#>
#> Following methods can be applied to this 'ConsensusPartition' object:
#> [1] "cola_report" "collect_classes" "collect_plots"
#> [4] "collect_stats" "colnames" "compare_partitions"
#> [7] "compare_signatures" "consensus_heatmap" "dimension_reduction"
#> [10] "functional_enrichment" "get_anno_col" "get_anno"
#> [13] "get_classes" "get_consensus" "get_matrix"
#> [16] "get_membership" "get_param" "get_signatures"
#> [19] "get_stats" "is_best_k" "is_stable_k"
#> [22] "membership_heatmap" "ncol" "nrow"
#> [25] "plot_ecdf" "predict_classes" "rownames"
#> [28] "select_partition_number" "show" "suggest_best_k"
#> [31] "test_to_known_factors" "top_rows_heatmap"
collect_plots() function collects all the plots made from res for all k (number of subgroups)
into one single page to provide an easy and fast comparison between different k.
collect_plots(res)
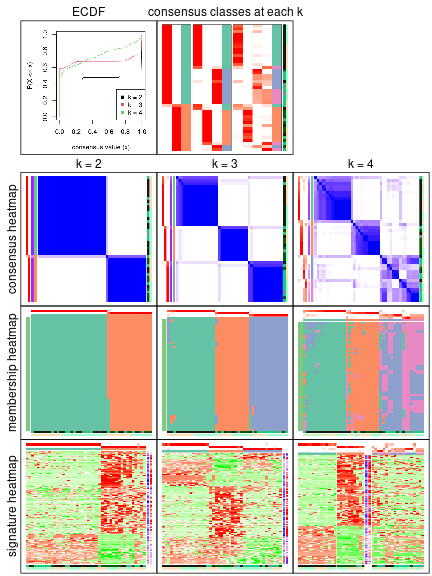
The plots are:
k and the heatmap of
predicted classes for each k.k.k.k.All the plots in panels can be made by individual functions and they are plotted later in this section.
select_partition_number() produces several plots showing different
statistics for choosing “optimized” k. There are following statistics:
k;k, the area increased is defined as \(A_k - A_{k-1}\).The detailed explanations of these statistics can be found in the cola vignette.
Generally speaking, higher 1-PAC score, higher mean silhouette score or higher
concordance corresponds to better partition. Rand index and Jaccard index
measure how similar the current partition is compared to partition with k-1.
If they are too similar, we won't accept k is better than k-1.
select_partition_number(res)
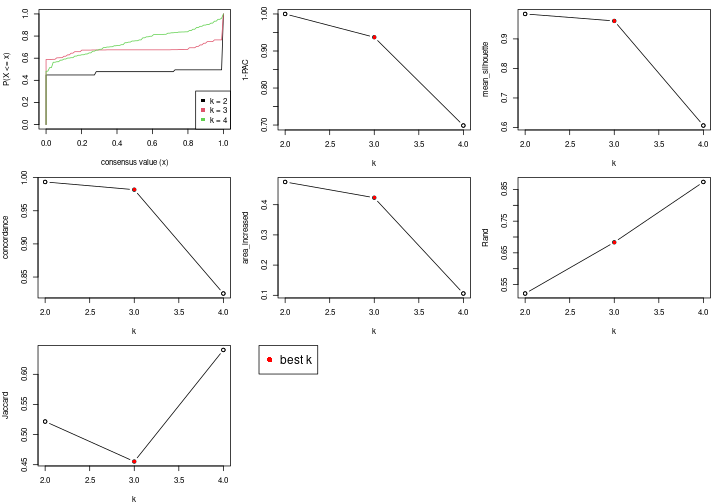
The numeric values for all these statistics can be obtained by get_stats().
get_stats(res)
#> k 1-PAC mean_silhouette concordance area_increased Rand Jaccard
#> 2 2 1.000 0.984 0.993 0.475 0.522 0.522
#> 3 3 0.937 0.961 0.982 0.423 0.683 0.455
#> 4 4 0.699 0.607 0.825 0.106 0.874 0.640
suggest_best_k() suggests the best \(k\) based on these statistics. The rules are as follows:
suggest_best_k(res)
#> [1] 3
#> attr(,"optional")
#> [1] 2
There is also optional best \(k\) = 2 that is worth to check.
Following is the table of the partitions (You need to click the show/hide
code output link to see it). The membership matrix (columns with name p*)
is inferred by
clue::cl_consensus()
function with the SE method. Basically the value in the membership matrix
represents the probability to belong to a certain group. The finall subgroup
label for an item is determined with the group with highest probability it
belongs to.
In get_classes() function, the entropy is calculated from the membership
matrix and the silhouette score is calculated from the consensus matrix.
cbind(get_classes(res, k = 2), get_membership(res, k = 2))
#> class entropy silhouette p1 p2
#> 10th_C42_S109 1 0.000 1.000 1.00 0.00
#> 10th_C63_S82 1 0.000 1.000 1.00 0.00
#> 10th_C77_S120 2 0.000 0.981 0.00 1.00
#> 10th_C80_S77 1 0.000 1.000 1.00 0.00
#> 10th_C86_S78 1 0.000 1.000 1.00 0.00
#> 10th_C87_S71 1 0.000 1.000 1.00 0.00
#> 11th-C26_S12 1 0.000 1.000 1.00 0.00
#> 11th-C2_S8 2 0.000 0.981 0.00 1.00
#> 11th-C43_S7 1 0.000 1.000 1.00 0.00
#> 11th-C4_S62 1 0.000 1.000 1.00 0.00
#> 11th-C55_S24 1 0.000 1.000 1.00 0.00
#> 11th-C56_S32 2 0.000 0.981 0.00 1.00
#> 11th-C64_S72 1 0.000 1.000 1.00 0.00
#> 11th-C77_S82 2 0.000 0.981 0.00 1.00
#> 12th-C36_S158 2 0.000 0.981 0.00 1.00
#> 12th-C53_S168 1 0.000 1.000 1.00 0.00
#> 12th-C56_S211 1 0.000 1.000 1.00 0.00
#> 13th_C27_S151 1 0.000 1.000 1.00 0.00
#> 13th_C36_S196 2 0.000 0.981 0.00 1.00
#> 13th_C49_S155 1 0.000 1.000 1.00 0.00
#> 13th_C72_S215 2 0.000 0.981 0.00 1.00
#> 13th_C8_S140 1 0.000 1.000 1.00 0.00
#> 2nd-C2_S2 2 0.000 0.981 0.00 1.00
#> 3rd-C51_S87 2 0.000 0.981 0.00 1.00
#> 4th-C27_S51 1 0.000 1.000 1.00 0.00
#> 5th-C10_S92 1 0.000 1.000 1.00 0.00
#> 5th-C11_S91 2 0.855 0.611 0.28 0.72
#> 5th-C16_S98 2 0.000 0.981 0.00 1.00
#> 5th-C25_S108 1 0.000 1.000 1.00 0.00
#> 5th-C40_S112 1 0.000 1.000 1.00 0.00
#> 5th-C42_S114 2 0.000 0.981 0.00 1.00
#> 5th-C43_S121 1 0.000 1.000 1.00 0.00
#> 5th-C45_S123 1 0.000 1.000 1.00 0.00
#> 5th-C56_S95 1 0.000 1.000 1.00 0.00
#> 5th-C58_S93 1 0.000 1.000 1.00 0.00
#> 5th-C67_S105 2 0.000 0.981 0.00 1.00
#> 5th-C73_S111 1 0.000 1.000 1.00 0.00
#> 5th-C81_S115 1 0.000 1.000 1.00 0.00
#> 5th-C88_S117 1 0.000 1.000 1.00 0.00
#> 7th-C76_S52 2 0.000 0.981 0.00 1.00
#> 7th-C81_S56 1 0.000 1.000 1.00 0.00
#> 9th-C22_S41 2 0.000 0.981 0.00 1.00
#> 9th-C2_S2 2 0.000 0.981 0.00 1.00
cbind(get_classes(res, k = 3), get_membership(res, k = 3))
#> class entropy silhouette p1 p2 p3
#> 10th_C42_S109 1 0.000 0.976 1.00 0.00 0.00
#> 10th_C63_S82 1 0.000 0.976 1.00 0.00 0.00
#> 10th_C77_S120 2 0.000 0.985 0.00 1.00 0.00
#> 10th_C80_S77 3 0.000 0.980 0.00 0.00 1.00
#> 10th_C86_S78 1 0.000 0.976 1.00 0.00 0.00
#> 10th_C87_S71 1 0.000 0.976 1.00 0.00 0.00
#> 11th-C26_S12 3 0.000 0.980 0.00 0.00 1.00
#> 11th-C2_S8 2 0.000 0.985 0.00 1.00 0.00
#> 11th-C43_S7 3 0.000 0.980 0.00 0.00 1.00
#> 11th-C4_S62 3 0.000 0.980 0.00 0.00 1.00
#> 11th-C55_S24 3 0.000 0.980 0.00 0.00 1.00
#> 11th-C56_S32 2 0.000 0.985 0.00 1.00 0.00
#> 11th-C64_S72 1 0.000 0.976 1.00 0.00 0.00
#> 11th-C77_S82 2 0.000 0.985 0.00 1.00 0.00
#> 12th-C36_S158 2 0.000 0.985 0.00 1.00 0.00
#> 12th-C53_S168 1 0.000 0.976 1.00 0.00 0.00
#> 12th-C56_S211 3 0.000 0.980 0.00 0.00 1.00
#> 13th_C27_S151 1 0.000 0.976 1.00 0.00 0.00
#> 13th_C36_S196 2 0.000 0.985 0.00 1.00 0.00
#> 13th_C49_S155 3 0.000 0.980 0.00 0.00 1.00
#> 13th_C72_S215 2 0.400 0.805 0.00 0.84 0.16
#> 13th_C8_S140 3 0.000 0.980 0.00 0.00 1.00
#> 2nd-C2_S2 2 0.000 0.985 0.00 1.00 0.00
#> 3rd-C51_S87 2 0.000 0.985 0.00 1.00 0.00
#> 4th-C27_S51 3 0.369 0.835 0.14 0.00 0.86
#> 5th-C10_S92 1 0.000 0.976 1.00 0.00 0.00
#> 5th-C11_S91 1 0.207 0.927 0.94 0.06 0.00
#> 5th-C16_S98 3 0.296 0.882 0.00 0.10 0.90
#> 5th-C25_S108 3 0.000 0.980 0.00 0.00 1.00
#> 5th-C40_S112 1 0.455 0.744 0.80 0.00 0.20
#> 5th-C42_S114 1 0.334 0.865 0.88 0.12 0.00
#> 5th-C43_S121 3 0.000 0.980 0.00 0.00 1.00
#> 5th-C45_S123 1 0.000 0.976 1.00 0.00 0.00
#> 5th-C56_S95 1 0.000 0.976 1.00 0.00 0.00
#> 5th-C58_S93 1 0.000 0.976 1.00 0.00 0.00
#> 5th-C67_S105 2 0.000 0.985 0.00 1.00 0.00
#> 5th-C73_S111 1 0.000 0.976 1.00 0.00 0.00
#> 5th-C81_S115 1 0.000 0.976 1.00 0.00 0.00
#> 5th-C88_S117 1 0.000 0.976 1.00 0.00 0.00
#> 7th-C76_S52 2 0.000 0.985 0.00 1.00 0.00
#> 7th-C81_S56 3 0.000 0.980 0.00 0.00 1.00
#> 9th-C22_S41 3 0.000 0.980 0.00 0.00 1.00
#> 9th-C2_S2 2 0.000 0.985 0.00 1.00 0.00
cbind(get_classes(res, k = 4), get_membership(res, k = 4))
#> class entropy silhouette p1 p2 p3 p4
#> 10th_C42_S109 1 0.3610 0.7898 0.80 0.00 0.20 0.00
#> 10th_C63_S82 1 0.1913 0.8771 0.94 0.00 0.02 0.04
#> 10th_C77_S120 2 0.0000 0.8746 0.00 1.00 0.00 0.00
#> 10th_C80_S77 3 0.0000 0.4887 0.00 0.00 1.00 0.00
#> 10th_C86_S78 1 0.4522 0.6433 0.68 0.00 0.32 0.00
#> 10th_C87_S71 1 0.0000 0.8997 1.00 0.00 0.00 0.00
#> 11th-C26_S12 3 0.1211 0.4791 0.00 0.00 0.96 0.04
#> 11th-C2_S8 2 0.0000 0.8746 0.00 1.00 0.00 0.00
#> 11th-C43_S7 4 0.4948 0.4587 0.00 0.00 0.44 0.56
#> 11th-C4_S62 4 0.4977 0.3588 0.00 0.00 0.46 0.54
#> 11th-C55_S24 3 0.4948 -0.3056 0.00 0.00 0.56 0.44
#> 11th-C56_S32 2 0.2830 0.8212 0.00 0.90 0.04 0.06
#> 11th-C64_S72 1 0.0000 0.8997 1.00 0.00 0.00 0.00
#> 11th-C77_S82 2 0.1211 0.8682 0.00 0.96 0.00 0.04
#> 12th-C36_S158 2 0.0000 0.8746 0.00 1.00 0.00 0.00
#> 12th-C53_S168 1 0.0000 0.8997 1.00 0.00 0.00 0.00
#> 12th-C56_S211 4 0.4948 0.4587 0.00 0.00 0.44 0.56
#> 13th_C27_S151 1 0.0707 0.8945 0.98 0.00 0.02 0.00
#> 13th_C36_S196 2 0.4994 0.3974 0.00 0.52 0.00 0.48
#> 13th_C49_S155 4 0.4948 0.4587 0.00 0.00 0.44 0.56
#> 13th_C72_S215 4 0.1211 0.3558 0.00 0.04 0.00 0.96
#> 13th_C8_S140 3 0.4948 -0.3082 0.00 0.00 0.56 0.44
#> 2nd-C2_S2 2 0.1211 0.8682 0.00 0.96 0.00 0.04
#> 3rd-C51_S87 2 0.0000 0.8746 0.00 1.00 0.00 0.00
#> 4th-C27_S51 3 0.7888 -0.0835 0.32 0.00 0.38 0.30
#> 5th-C10_S92 1 0.1637 0.8830 0.94 0.00 0.06 0.00
#> 5th-C11_S91 1 0.6797 0.4216 0.60 0.24 0.00 0.16
#> 5th-C16_S98 4 0.0000 0.3748 0.00 0.00 0.00 1.00
#> 5th-C25_S108 3 0.4277 0.3602 0.00 0.00 0.72 0.28
#> 5th-C40_S112 4 0.4797 0.1453 0.26 0.00 0.02 0.72
#> 5th-C42_S114 2 0.5570 0.1826 0.44 0.54 0.02 0.00
#> 5th-C43_S121 4 0.4855 0.4544 0.00 0.00 0.40 0.60
#> 5th-C45_S123 1 0.0000 0.8997 1.00 0.00 0.00 0.00
#> 5th-C56_S95 1 0.0000 0.8997 1.00 0.00 0.00 0.00
#> 5th-C58_S93 1 0.3821 0.8216 0.84 0.00 0.12 0.04
#> 5th-C67_S105 2 0.2611 0.8473 0.04 0.92 0.02 0.02
#> 5th-C73_S111 1 0.0000 0.8997 1.00 0.00 0.00 0.00
#> 5th-C81_S115 1 0.0000 0.8997 1.00 0.00 0.00 0.00
#> 5th-C88_S117 1 0.3400 0.8086 0.82 0.00 0.18 0.00
#> 7th-C76_S52 2 0.3821 0.8077 0.04 0.84 0.00 0.12
#> 7th-C81_S56 3 0.0707 0.4884 0.00 0.00 0.98 0.02
#> 9th-C22_S41 3 0.6720 0.2985 0.00 0.12 0.58 0.30
#> 9th-C2_S2 2 0.0000 0.8746 0.00 1.00 0.00 0.00
Heatmaps for the consensus matrix. It visualizes the probability of two samples to be in a same group.
consensus_heatmap(res, k = 2)
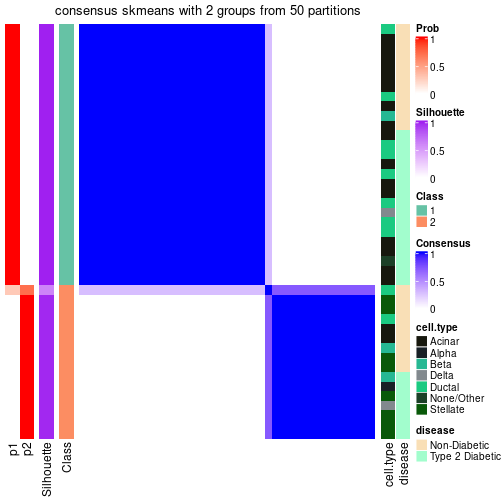
consensus_heatmap(res, k = 3)
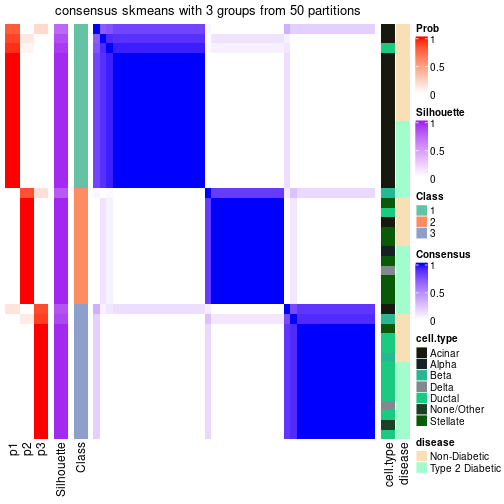
consensus_heatmap(res, k = 4)
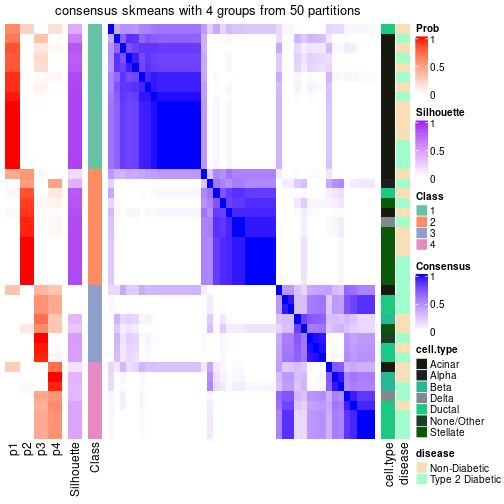
Heatmaps for the membership of samples in all partitions to see how consistent they are:
membership_heatmap(res, k = 2)
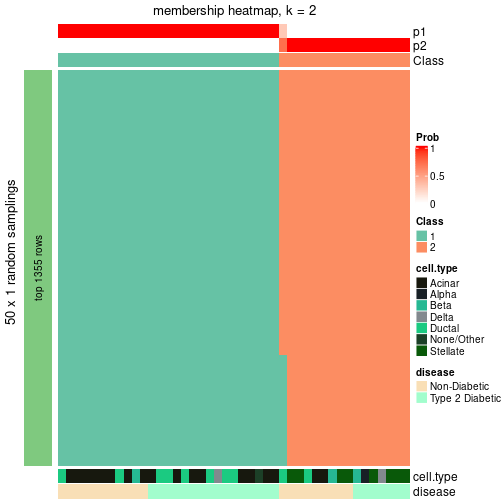
membership_heatmap(res, k = 3)
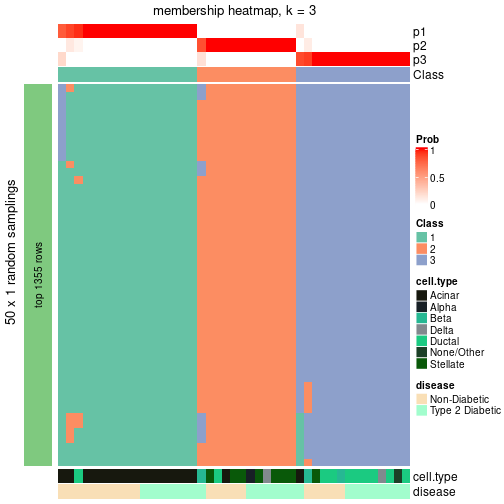
membership_heatmap(res, k = 4)
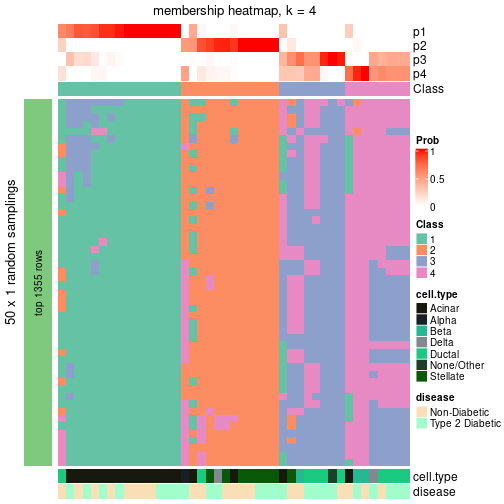
As soon as the classes for columns are determined, the signatures that are significantly different between subgroups can be looked for. Following are the heatmaps for signatures.
Signature heatmaps where rows are scaled:
Signature heatmaps where rows are not scaled:
get_signatures(res, k = 2, scale_rows = FALSE)
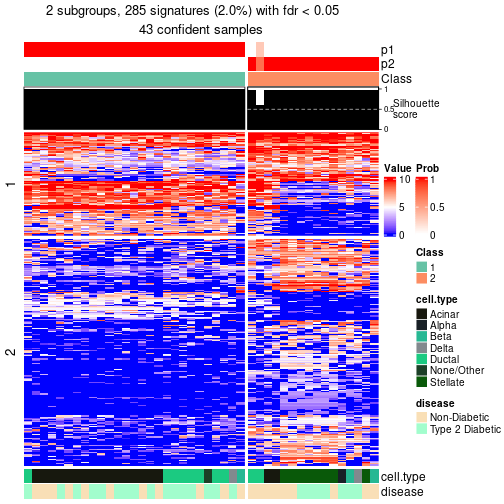
get_signatures(res, k = 3, scale_rows = FALSE)

get_signatures(res, k = 4, scale_rows = FALSE)
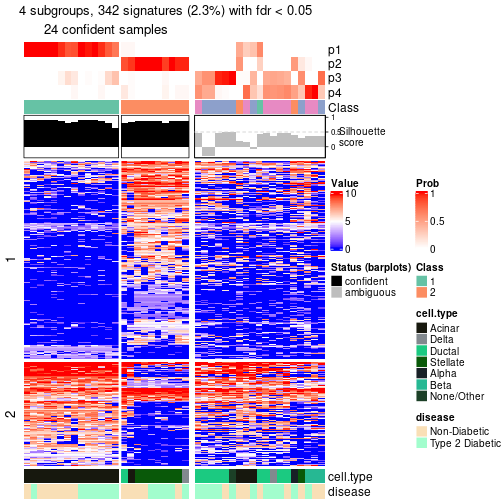
Compare the overlap of signatures from different k:
compare_signatures(res)
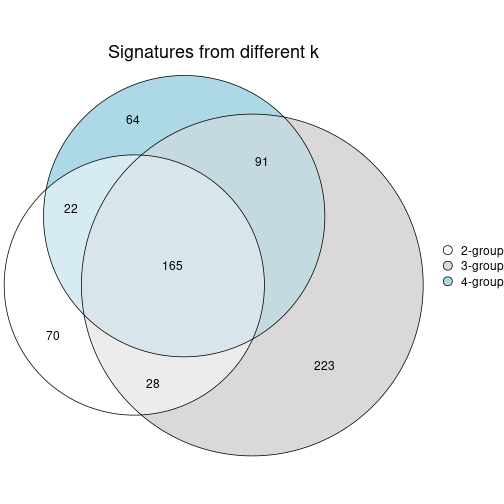
get_signature() returns a data frame invisibly. To get the list of signatures, the function
call should be assigned to a variable explicitly. In following code, if plot argument is set
to FALSE, no heatmap is plotted while only the differential analysis is performed.
# code only for demonstration
tb = get_signature(res, k = ..., plot = FALSE)
An example of the output of tb is:
#> which_row fdr mean_1 mean_2 scaled_mean_1 scaled_mean_2 km
#> 1 38 0.042760348 8.373488 9.131774 -0.5533452 0.5164555 1
#> 2 40 0.018707592 7.106213 8.469186 -0.6173731 0.5762149 1
#> 3 55 0.019134737 10.221463 11.207825 -0.6159697 0.5749050 1
#> 4 59 0.006059896 5.921854 7.869574 -0.6899429 0.6439467 1
#> 5 60 0.018055526 8.928898 10.211722 -0.6204761 0.5791110 1
#> 6 98 0.009384629 15.714769 14.887706 0.6635654 -0.6193277 2
...
The columns in tb are:
which_row: row indices corresponding to the input matrix.fdr: FDR for the differential test. mean_x: The mean value in group x.scaled_mean_x: The mean value in group x after rows are scaled.km: Row groups if k-means clustering is applied to rows (which is done by automatically selecting number of clusters).If there are too many signatures, top_signatures = ... can be set to only show the
signatures with the highest FDRs:
# code only for demonstration
# e.g. to show the top 500 most significant rows
tb = get_signature(res, k = ..., top_signatures = 500)
If the signatures are defined as these which are uniquely high in current group, diff_method argument
can be set to "uniquely_high_in_one_group":
# code only for demonstration
tb = get_signature(res, k = ..., diff_method = "uniquely_high_in_one_group")
UMAP plot which shows how samples are separated.
dimension_reduction(res, k = 2, method = "UMAP")
dimension_reduction(res, k = 3, method = "UMAP")
dimension_reduction(res, k = 4, method = "UMAP")
Following heatmap shows how subgroups are split when increasing k:
collect_classes(res)
Test correlation between subgroups and known annotations. If the known annotation is numeric, one-way ANOVA test is applied, and if the known annotation is discrete, chi-squared contingency table test is applied.
test_to_known_factors(res)
#> n_sample cell.type(p-value) disease(p-value) k
#> ATC:skmeans 43 6.32e-04 0.503 2
#> ATC:skmeans 43 8.53e-07 0.406 3
#> ATC:skmeans 24 1.57e-04 1.000 4
If matrix rows can be associated to genes, consider to use functional_enrichment(res,
...) to perform function enrichment for the signature genes. See this vignette for more detailed explanations.
sessionInfo()
#> R version 4.1.0 (2021-05-18)
#> Platform: x86_64-pc-linux-gnu (64-bit)
#> Running under: CentOS Linux 7 (Core)
#>
#> Matrix products: default
#> BLAS/LAPACK: /usr/lib64/libopenblas-r0.3.3.so
#>
#> locale:
#> [1] LC_CTYPE=en_US.UTF-8 LC_NUMERIC=C LC_TIME=en_US.UTF-8
#> [4] LC_COLLATE=en_US.UTF-8 LC_MONETARY=en_US.UTF-8 LC_MESSAGES=en_US.UTF-8
#> [7] LC_PAPER=en_US.UTF-8 LC_NAME=C LC_ADDRESS=C
#> [10] LC_TELEPHONE=C LC_MEASUREMENT=en_US.UTF-8 LC_IDENTIFICATION=C
#>
#> attached base packages:
#> [1] grid parallel stats4 stats graphics grDevices utils datasets methods
#> [10] base
#>
#> other attached packages:
#> [1] genefilter_1.74.0 ComplexHeatmap_2.8.0 markdown_1.1
#> [4] knitr_1.33 scRNAseq_2.6.1 SingleCellExperiment_1.14.1
#> [7] SummarizedExperiment_1.22.0 Biobase_2.52.0 GenomicRanges_1.44.0
#> [10] GenomeInfoDb_1.28.1 IRanges_2.26.0 S4Vectors_0.30.0
#> [13] BiocGenerics_0.38.0 MatrixGenerics_1.4.0 matrixStats_0.59.0
#> [16] cola_1.9.4
#>
#> loaded via a namespace (and not attached):
#> [1] circlize_0.4.13 AnnotationHub_3.0.1 BiocFileCache_2.0.0
#> [4] lazyeval_0.2.2 polylabelr_0.2.0 splines_4.1.0
#> [7] Polychrome_1.3.1 BiocParallel_1.26.1 ggplot2_3.3.5
#> [10] digest_0.6.27 foreach_1.5.1 ensembldb_2.16.3
#> [13] htmltools_0.5.1.1 viridis_0.6.1 fansi_0.5.0
#> [16] magrittr_2.0.1 memoise_2.0.0 cluster_2.1.2
#> [19] doParallel_1.0.16 Biostrings_2.60.1 annotate_1.70.0
#> [22] askpass_1.1 prettyunits_1.1.1 colorspace_2.0-2
#> [25] blob_1.2.1 rappdirs_0.3.3 xfun_0.24
#> [28] dplyr_1.0.7 crayon_1.4.1 RCurl_1.98-1.3
#> [31] microbenchmark_1.4-7 jsonlite_1.7.2 impute_1.66.0
#> [34] brew_1.0-6 survival_3.2-11 iterators_1.0.13
#> [37] glue_1.4.2 polyclip_1.10-0 gtable_0.3.0
#> [40] zlibbioc_1.38.0 XVector_0.32.0 GetoptLong_1.0.5
#> [43] DelayedArray_0.18.0 shape_1.4.6 scales_1.1.1
#> [46] data.tree_1.0.0 DBI_1.1.1 Rcpp_1.0.7
#> [49] viridisLite_0.4.0 xtable_1.8-4 progress_1.2.2
#> [52] clue_0.3-59 reticulate_1.20 bit_4.0.4
#> [55] mclust_5.4.7 umap_0.2.7.0 httr_1.4.2
#> [58] RColorBrewer_1.1-2 ellipsis_0.3.2 pkgconfig_2.0.3
#> [61] XML_3.99-0.6 dbplyr_2.1.1 utf8_1.2.1
#> [64] tidyselect_1.1.1 rlang_0.4.11 later_1.2.0
#> [67] AnnotationDbi_1.54.1 munsell_0.5.0 BiocVersion_3.13.1
#> [70] tools_4.1.0 cachem_1.0.5 generics_0.1.0
#> [73] RSQLite_2.2.7 ExperimentHub_2.0.0 evaluate_0.14
#> [76] stringr_1.4.0 fastmap_1.1.0 yaml_2.2.1
#> [79] bit64_4.0.5 purrr_0.3.4 dendextend_1.15.1
#> [82] KEGGREST_1.32.0 AnnotationFilter_1.16.0 mime_0.11
#> [85] slam_0.1-48 xml2_1.3.2 biomaRt_2.48.2
#> [88] compiler_4.1.0 rstudioapi_0.13 filelock_1.0.2
#> [91] curl_4.3.2 png_0.1-7 interactiveDisplayBase_1.30.0
#> [94] tibble_3.1.2 stringi_1.7.3 highr_0.9
#> [97] GenomicFeatures_1.44.0 RSpectra_0.16-0 lattice_0.20-44
#> [100] ProtGenerics_1.24.0 Matrix_1.3-4 vctrs_0.3.8
#> [103] pillar_1.6.1 lifecycle_1.0.0 BiocManager_1.30.16
#> [106] eulerr_6.1.0 GlobalOptions_0.1.2 bitops_1.0-7
#> [109] irlba_2.3.3 httpuv_1.6.1 rtracklayer_1.52.0
#> [112] R6_2.5.0 BiocIO_1.2.0 promises_1.2.0.1
#> [115] gridExtra_2.3 codetools_0.2-18 assertthat_0.2.1
#> [118] openssl_1.4.4 rjson_0.2.20 GenomicAlignments_1.28.0
#> [121] Rsamtools_2.8.0 GenomeInfoDbData_1.2.6 hms_1.1.0
#> [124] skmeans_0.2-13 Cairo_1.5-12.2 scatterplot3d_0.3-41
#> [127] shiny_1.6.0 restfulr_0.0.13